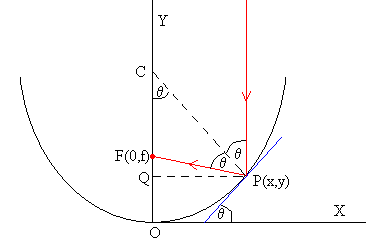
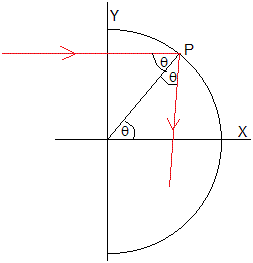
Consideremos la superficie de un espejo descrita por la curva y(x) que es simétrica y(x)=y(-x) siendo el eje Y el eje de simetría. Trazamos un rayo de luz paralelo al eje Y, que corta a la superficie del espejo en el punto P de coordenadas (x,y). El ángulo de incidencia, formado por el rayo de luz incidente y la normal a la superficie es θ. De acuerdo con la ley de la reflexión, el ángulo formado por el rayo reflejado y la normal es también θ. El rayo reflejado corta al eje Y en el punto F(0,f).

El ángulo θ es el ángulo de la recta tangente a la curva y(x) en el punto P de abscisa x.

${\displaystyle \tan \theta =\frac{dy}{dx}}$

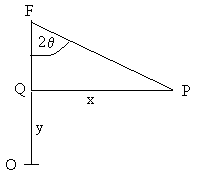
En el triángulo FPQ, el ángulo QFP es 2θ, por lo que el lado FQ vale x/tan(2θ), así pues la posición f es

${\displaystyle \begin{array}{l}f=y+\frac{x}{\tan (2\theta )}\\ \tan (2\theta )=\frac{2\tan \theta }{1-{\tan }^2\theta }\\ f=y+\frac{x\left(1-{\tan }^2\theta \right)}{2\tan \theta }=y+\frac{x\left(1-{\left(dy/dx\right)}^2\right)}{2\left(dy/dx\right)}\end{array}}$

Espejo esférico

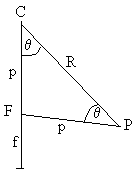
En un espejo esférico C es el centro del arco de circunferencia de radio R. Este centro es fijo de modo que OC es igual a CP igual al radio R de la circunferencia. Por otra parte, el triángulo CFP es isósceles y la longitud FP es igual a FC, denominamos p a esta longitud.

${\displaystyle \begin{array}{l}{R}^2=p^2+p^2-2pp\cos \left(180-2\theta \right)\\ R^2=2p^2+2p^2\cos \left(2\theta \right)=4p^2{\cos }^2\theta \\ p=\frac{R}{2\cos \theta }\end{array}}$

Como f+p=R es el radio de la circunferencia.

${\displaystyle f=R\left(1-\frac{1}{2\cos \theta }\right)}$

Para un espejo esférico cóncavo el foco no es único, depende del ángulo θ. Si el ángulo θ es pequeño, se puede hacer la aproximación

${\displaystyle \begin{array}{l}\cos \theta \approx 1\\ f\approx \frac{1}{2}R\theta \ll 1\end{array}}$

Se puede obtener el mismo resultado a partir de la ecuación del arco de circunferencia de centro C(0,R)

${\displaystyle \begin{array}{l}{x}^2+{\left(y-R\right)}^2=R^2\\ y^2-2Ry+x^2=0\\ y=R-\sqrt{R^2-x^2}\\ \tan \theta =\frac{dy}{dx}=\frac{x}{\sqrt{R^2-x^2}}\\ f=y+\frac{x\left(1-{\tan }^2\theta \right)}{2\tan \theta }=R\left(1-\frac{R}{2\sqrt{R^2-x^2}}\right)\end{array}}$

En la figura, vemos que en el triángulo rectángulo CPQ,

${\displaystyle CQ=\sqrt{R^2-x^2}CQ=R\cos \theta }$

Llegamos al mismo resultado para el cálculo de f

R=1; %radio del espejo esférico cóncavo
angMax=40; %ángulo de apertura
ang=-angMax:angMax;
x=R*sind(ang);
y=R-R*cosd(ang);
hold on

%espejo esférico
plot(x,y,'k')
xx=[x(1),x,x(end)];
yy=[-0.2,y,-0.2];
fill(xx,yy,'k')
axis equal
ylim([-0.2,R+0.2])

%rayos
xc=fix(x(1)*10)/10:0.1:-fix(x(1)*10)/10;
angulo=asin(xc/R);
yc=R-R*cos(angulo);
f=R*(1-0.5./cos(angulo));
for i=1:length(xc)
    line([xc(i),xc(i)],[R+0.2,yc(i)]) %incidentes
    hl=line([xc(i),0],[yc(i),f(i)]); %reflejados
    set(hl,'color','r')
end

hold off
title('Espejo esférico')
xlabel('x')
ylabel('y')

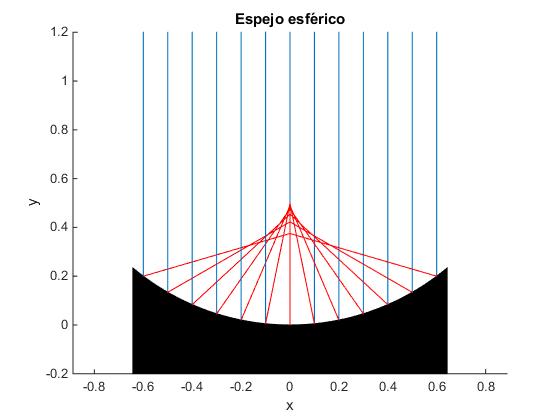
En la figura, vemos que los rayos reflejados (en color rojo) no convergen en un punto.

Ecuación de la envolvente

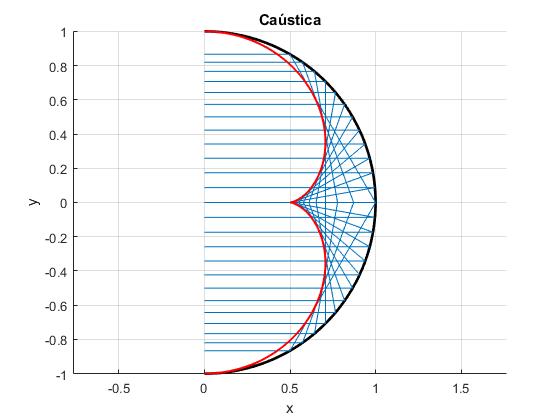
Vamos a determinar la ecuación de la envolvente de los rayos reflejados en el espejo esférico

La ecuación del rayo reflejado que pasa por el punto P (cosθ, sinθ) y tiene pendiente 2θ es

y=tan(2θ)·x+sinθ-tan(2θ)·cosθ

(y-sinθ)·cos(2θ)=(x-cosθ)·sin(2θ)

Simplificando

ycos(2θ)+sinθ=xsin(2θ)

La ecuación de la envolvente de los rayos reflejados se obtiene derivando la ecuación de la recta, f(x,y,θ)=0 con respecto a θ e igualando a cero.

${\displaystyle \frac{\partial f}{\partial \theta }=0}$

-cosθ·cos(2θ)-(y-sinθ)2·sin(2θ)=sinθ·sin(2θ)+(y-cosθ)2·cos(2θ)

Simplificando

-2ysin(2θ)+cosθ=2xcos(2θ)

Resolvemos el sistema de dos ecuaciones con dos incógnitas, despejando x e y, obteniendo la ecuación de la envolvente en forma paramétrica

${\displaystyle \begin{array}{l}x=\frac{3}{2}\cos \theta -{\cos }^3\theta \\ y={\sin }^3\theta \end{array}}$

hold on
%espejo esférico
th=linspace(-pi/2,pi/2, 200);
plot(cos(th),sin(th), 'k', 'lineWidth',2)
%rayos incidentes y reflejados
for th=-pi/2+pi/6:pi/36:pi/2-pi/6
    line([0,cos(th)],[sin(th),sin(th)])
    line([cos(th),0.5/cos(th)],[sin(th),0])
end
%envolvente   
th=linspace(-pi/2,pi/2, 200);
x=3*cos(th)/2-cos(th).^3;
y=sin(th).^3;
plot(x,y,'r', 'lineWidth',1.5)
hold off
axis equal
grid on
xlabel('x')
ylabel('y')
title('Caústica')

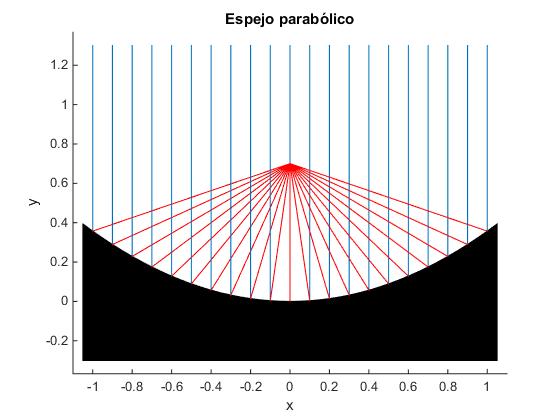
Espejo parabólico

Consideremos la parábola descrita por la ecuación y=ax², la pendiente

${\displaystyle \begin{array}{l}\frac{dy}{dx}=2ax\\ f=y+\frac{x\left(1-{\left(dy/dx\right)}^2\right)}{2\left(dy/dx\right)}=a{x}^2+\frac{x\left(1-4a^2{x}^2\right)}{4ax}=\frac{1}{4a}\end{array}}$

El foco f es independiente de x. Todos los rayos paralelos al eje Y pasan por el foco F después de reflejarse en el espejo.

La ecuación de una parábola de foco f es

${\displaystyle y=\frac{x^2}{4f}}$

f=0.7; %posición del foco (cambiar)
a=1.0; %apertura es 2a (mantener fijo)
x=-a-.05:0.05:a+0.05;
y=x.^2/(4*f);
hold on

%espejo parabólico
plot(x,y,'k')
xx=[x(1),x,x(end)];
yy=[-0.3,y,-0.3];
fill(xx,yy,'k')
axis equal
xlim([-a-0.1,a+0.1])

%rayos
xc=fix(x(1)*10)/10:0.1:-fix(x(1)*10)/10;
yc=xc.^2/(4*f);
for i=1:length(xc)
    line([xc(i),xc(i)],[a+0.3,yc(i)]) %incidentes
    hl=line([xc(i),0],[yc(i),f]);  %reflejados
    set(hl,'color','r')
end

hold off
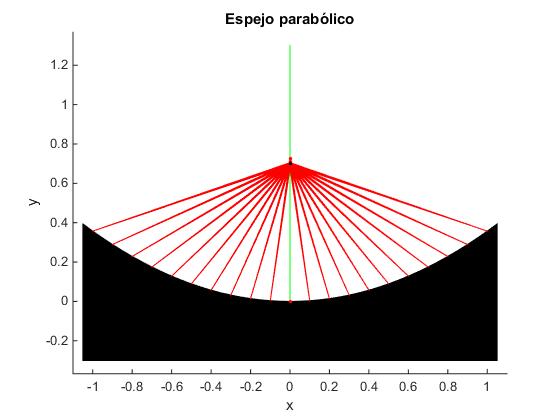
title('Espejo parabólico')
xlabel('x')
ylabel('y')

Demostramos ahora, que la parábola es la única la curva y=y(x) que tiene la propiedad de que todos los rayos paralelos al eje Y pasan por el foco F. Si f no depende de x, df/dx=0. Derivamos la expresión de f dada al principio de esta página y válida para cualquier superficie y(x)

${\displaystyle \begin{array}{l}\frac{dy}{dx}+\frac{\left\{1-{\left(dy/dx\right)}^2-2x\left(dy/dx\right)\left(d^{2}y/d{x}^2\right)\right\}\left(dy/dx\right)}{2{\left(dy/dx\right)}^2}\\ \frac{-x\left(1-{\left(dy/dx\right)}^2\right)\left(d^{2}y/d{x}^2\right)}{2{\left(dy/dx\right)}^2}=0\\ \frac{dy}{dx}-x{\left(\frac{dy}{dx}\right)}^2\frac{d^{2}y}{d{x}^2}-x\frac{d^{2}y}{d{x}^2}+{\left(\frac{dy}{dx}\right)}^3=0\\ \left(1+{\left(\frac{dy}{dx}\right)}^2\right)\left(\frac{dy}{dx}-x\frac{d^{2}y}{d{x}^2}\right)=0\\ \frac{dy}{dx}-x\frac{d^{2}y}{d{x}^2}=0\\ y=A{x}^2+B\end{array}}$

Resolvemos la ecuación diferencial utilizando Math Symbolic. Llamamos t a x y x a y.

>> dsolve('t*D2x-Dx=0')
ans =C3*t^2 + C2

Los rayos de luz paralelos inciden en la parábola inclinados un ángulo δ.

Continuamos ahora con el estudio del espejo parabólico de distancia focial f. Como hemos visto en la página anterior, la ecuación de la superficie del espejo es

${\displaystyle y=\frac{x^2}{4f}}$

Supondremos ahora, que los rayos de luz paralelos inciden en la parábola inclinados un ángulo δ, respecto del eje Y tal como se muestra en la figura de la izquierda.

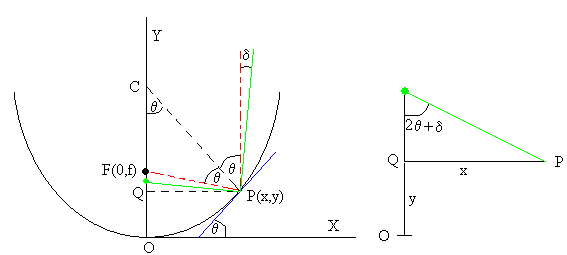
El rayo de color verde forma un ángulo δ con el eje Y, incide en el espejo parabólico en P, el ángulo de incidencia (el que forma el rayo incidente con la normal) es θ+δ, el ángulo que forma el rayo reflejado con la normal es θ+δ. Este rayo corta al eje Y en un punto marcado por un círculo verde. Como vemos en la figura de la derecha, la ordenada de ese punto vale

${\displaystyle \begin{array}{l}\tan \theta =\frac{dy}{dx}=\frac{x}{2f}\\ y_f=y+\frac{x}{\tan (2\theta +\delta )}\end{array}}$

f=0.7; %posición del foco (cambiar)
a=1.0; %apertura es 2a (mantener fijo)
x=-a-.05:0.05:a+0.05;
y=x.^2/(4*f);
delta=3; %inclinación de los rayos paralelos en grados
hold on

%espejo parabólico
plot(x,y,'k')
xx=[x(1),x,x(end)];
yy=[-0.3,y,-0.3];
fill(xx,yy,'k')
axis equal
xlim([-a-0.1,a+0.1])

%rayos
xc=fix(x(1)*10)/10:0.1:-fix(x(1)*10)/10;
yc=xc.^2/(4*f);
angulo=atan(xc/(2*f)); %pendiente
 %intersección del rayo reflejado con el eje Y
yf=yc+xc./tan(2*angulo+delta*pi/180);
hl=line([0,0],[0,a+0.3]);
set(hl,'color','g')
for i=1:length(xc)
    line([xc(i),xc(i)+(a+0.3-yc(i))*tand(delta)],[yc(i),(a+0.3)]);
    hl=line([xc(i),0],[yc(i),yf(i)]);  %reflejados
    set(hl,'color','r')
end
%intersección con el eje Y
plot(0,yf,'ro','markersize',2,'markeredgecolor','r','markerfacecolor','r')
%foco de la parábola
plot(0,f,'ko','markersize',2,'markeredgecolor','k','markerfacecolor','k') 
hold off
title('Espejo parabólico')
xlabel('x')
ylabel('y')

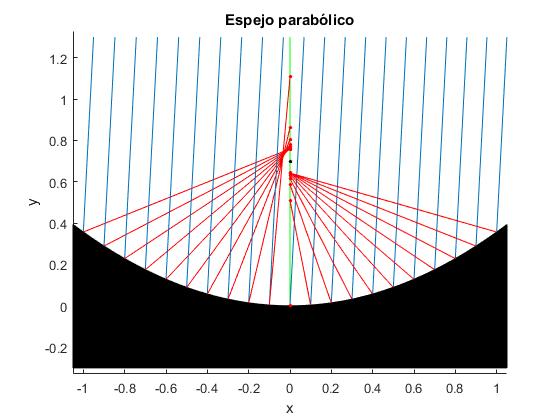
Los rayos reflejados no se concentran en el foco (marcado por un punto de color negro). Con un punto de color rojo marcamos la intersección de los rayos reflejados con el eje Y (en color verde)

Tamaño finito del Sol

Debido al tamaño finito del Sol, los espejos parabólicos no pueden concentrar los rayos del Sol en el foco de la parábola. El tamaño angular medio del Sol es de 31' 59" ≈32'=32/60 de grado, algo menos de medio grado.

En esta ocasión, dibujaremos los rayos reflejados para cada uno de los puntos seleccionados del espejo parabólico, de tres rayos incidentes:

• Un rayo incidente paralelo al eje Y
• Un rayo que forma un ángulo δ=16' con el eje Y
• Un rayo que forma un ángulo δ=-16' con el eje Y

f=0.7; %posición del foco (cambiar)
a=1.0; %apertura es 2a (mantener fijo)
x=-a-.05:0.05:a+0.05;
y=x.^2/(4*f);
delta=3; %inclinación de los rayos paralelos en grados
hold on

%espejo parabólico
plot(x,y,'k')
xx=[x(1),x,x(end)];
yy=[-0.3,y,-0.3];
fill(xx,yy,'k')
axis equal
xlim([-a-0.1,a+0.1])

%rayos
xc=fix(x(1)*10)/10:0.1:-fix(x(1)*10)/10;
yc=xc.^2/(4*f);
angulo=atan(xc/(2*f)); %pendiente
hl=line([0,0],[0,a+0.3]);
set(hl,'color','g')
for delta=[-16/60,0,16/60]
%intersección del rayo reflejado con el eje Y
    yf=yc+xc./tan(2*angulo+delta*pi/180); 
    for i=1:length(xc)
        hl=line([xc(i),0],[yc(i),yf(i)]);  %reflejados
        set(hl,'color','r')
    end
    %intersección con el eje Y
    plot(0,yf,'ro','markersize',2,'markeredgecolor','r',
'markerfacecolor','r')
end
%foco de la parábola
plot(0,f,'ko','markersize',2,'markeredgecolor','k',
'markerfacecolor','k') 
hold off
title('Espejo parabólico')
xlabel('x')
ylabel('y')