Campo eléctrico producido por dos hilos rectilíneos cargados

En este apartado, estudiaremos dos casos

Cargas de mismo signo

Calculamos el campo eléctrico producido en el punto P por un hilo rectilíneo cargado λ C/m, perpendicular al plano de la figura y que pasa por el punto (-a,0) y otro paralelo, con la misma carga, que pasa por el punto (a,0)

${\displaystyle \begin{array}{l}\overrightarrow{E_1}=\frac{\lambda }{2\pi {\epsilon }_0}\frac{\overrightarrow{r_1}}{r_1^2},\overrightarrow{E_2}=\frac{\lambda }{2\pi {\epsilon }_0}\frac{\overrightarrow{r_2}}{r_2^2}\\ r_1^2={\left(x+a\right)}^2+y^2,{\overrightarrow{r}}_1=(x+a)\widehat{i}+y\widehat{j}\\ r_2^2={\left(x-a\right)}^2+y^2,{\overrightarrow{r}}_2=(x-a)\widehat{i}+y\widehat{j}\end{array}}$

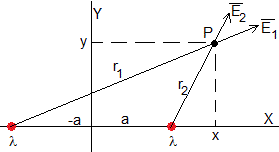
Sumamos vectorialmente los dos campos, simplificamos y obtenemos el siguiente resultado

${\displaystyle \overrightarrow{E}=\overrightarrow{E_1}+\overrightarrow{E_2}=\frac{\lambda }{\pi {\epsilon }_0}\frac{x\left(x^2+y^2-a^2\right)\widehat{i}+y\left(x^2+y^2+a^2\right)\widehat{j}}{a^4+{\left(x^2+y^2\right)}^2+2a^2\left(y^2-x^2\right)}}$

Diferencia de potencial

${\displaystyle \begin{array}{l}{V}_1(r_1)-V(r_0)=-\frac{\lambda }{2\pi {\epsilon }_0}\ln \left(\frac{r_1}{r_0}\right)\\ V_2(r_1)-V(r_0)=-\frac{\lambda }{2\pi {\epsilon }_0}\ln \left(\frac{r_2}{r_0}\right)\end{array}}$

La energía potencial está definida salvo una constante aditiva, que sirve para establecer el nivel cero de energía potencial

${\displaystyle V(r)=\frac{\lambda }{2\pi {\epsilon }_0}\ln \left(\frac{r_0^2}{r_1{r}_2}\right)}$

Cargas de signo contrario

Calculamos el campo eléctrico producido en el punto P por un hilo recilíneo cargado λ C/m, perpendicular al plano de la figura y que pasa por el punto (-a,0) y otro paralelo, con carga de signo contrario, que pasa por el punto (a,0)

${\displaystyle \begin{array}{l}\overrightarrow{E_1}=\frac{\lambda }{2\pi {\epsilon }_0}\frac{\overrightarrow{r_1}}{r_1^2},\overrightarrow{E_2}=-\frac{\lambda }{2\pi {\epsilon }_0}\frac{\overrightarrow{r_2}}{r_2^2}\\ r_1^2={\left(x+a\right)}^2+y^2,{\overrightarrow{r}}_1=(x+a)\widehat{i}+y\widehat{j}\\ r_2^2={\left(x-a\right)}^2+y^2,{\overrightarrow{r}}_2=(x-a)\widehat{i}+y\widehat{j}\end{array}}$

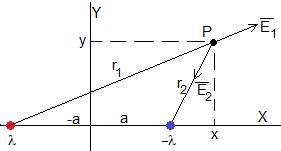
Sumamos vectorialmente los dos campos, simplificamos y obtenemos el siguiente resultado

${\displaystyle \overrightarrow{E}=\overrightarrow{E_1}+\overrightarrow{E_2}=\frac{\lambda }{\pi {\epsilon }_0}\frac{a\left(y^2+a^2-x^2\right)\widehat{i}-2axy\widehat{j}}{a^4+{\left(x^2+y^2\right)}^2+2a^2\left(y^2-x^2\right)}}$

Diferencia de potencial

${\displaystyle \begin{array}{l}{V}_1(r_1)-V(r_0)=-\frac{\lambda }{2\pi {\epsilon }_0}\ln \left(\frac{r_1}{r_0}\right)\\ V_2(r_1)-V(r_0)=\frac{\lambda }{2\pi {\epsilon }_0}\ln \left(\frac{r_2}{r_0}\right)\end{array}}$

Los potenciales son escalares y se suman

${\displaystyle V(x,y)=\frac{\lambda }{2\pi {\epsilon }_0}\ln \left(\frac{r_2}{r_1}\right)=\frac{\lambda }{4\pi {\epsilon }_0}\ln \left(\frac{{\left(x-a\right)}^2+y^2}{{\left(x+a\right)}^2+y^2}\right)}$

Equipotenciales

La ecuacón de la superficies equipotenciales o mejor, de las líneas en el plano perpendicular a los hilos rectilíneos cargados es

${\displaystyle \begin{array}{l}\frac{{\left(x-a\right)}^2+y^2}{{\left(x+a\right)}^2+y^2}=k\\ x^2+2a\frac{k+1}{k-1}x+a^2+y^2=0\end{array}}$

La expresamos como ecuación de una circunferencia con centro en (x₁, 0) y radio R

${\displaystyle \begin{array}{l}{\left(x-x_1\right)}^2+y^2=R^2\\ x^2-2x_{1}x+x_1^2+y^2=R^2\end{array}}$

Identificando términos,

${\displaystyle \begin{array}{l}\{\begin{array}{l}{x}_1=-a\frac{k+1}{k-1}\\ x_1^2-R^2=a^2\end{array}\\ {\left(x-\frac{1+k}{1-k}a\right)}^2+y^2=\frac{4k}{{\left(1-k\right)}^2}{a}^2\end{array}}$

Cuando k=1, tenemos una circunferencia de radio infinito con centro en el infinito, que representa el plano x=0

Líneas de fuerza

La ecuación diferencial de las líneas de fuerza es

${\displaystyle \frac{dy}{dx}=\frac{E_y}{E_x}}$

• la componente E_x es proporcional a y²+a²-x²
• la componente E_y es proporcional a -2xy

La ecuación de las líneas de fuerza es

${\displaystyle \begin{array}{l}\frac{dy}{dx}=\frac{-2xy}{y^2+a^2-x^2}\\ \left(y^2+a^2-x^2\right)dy+2xy·dx=0\\ \frac{d\left(x^2+y^2\right)}{a^2-\left(x^2+y^2\right)}+\frac{dy}{y}=0\end{array}}$

Integramos, llamando u=x²+y²

${\displaystyle \begin{array}{l}\frac{du}{a^2-u}+d\left(\ln y\right)=0\\ -\ln \left(a^2-u\right)+\ln y=\text{cte}\\ \frac{a^2-\left(x^2+y^2\right)}{y}=-2k\\ x^2+y^2-2k·y=a^2\end{array}}$

La expresamos como ecuación de una circunferencia de centro (0, y₁) y radio R

${\displaystyle \begin{array}{l}{x}^2+{\left(y-y_1\right)}^2=R^2\\ x^2+y^2-2y_{1}y+y_1^2=R^2\\ \{\begin{array}{l}{y}_1=k\\ R^2=k^2+a^2\end{array}\end{array}}$

Las circunferencias pasan por los puntos (-a,0) y (a,0), las posiciones de los hilos rectilíneos cargados

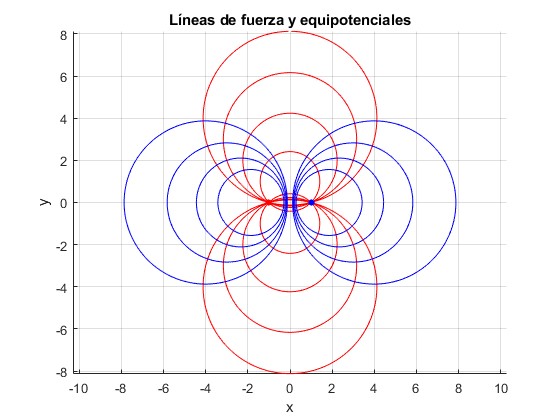
En color rojo representamos las líneas de fuerza y en azul las equipotenciales.

a=1; % 2a es la distancia entre los dos hilos
hold on
for k=[1:4, -(1:4)] %líneas de fuerza
   R=sqrt(a^2+k^2);
   y1=k;
   fplot(@(t) R*cos(t), @(t) y1+R*sin(t),[0,2*pi],'r')
end
for k=[0.3:0.1:0.6, 1./(0.3:0.1:0.6)] %equipotenciales
   R=2*a*sqrt(k)/(1-k);
   x1=(1+k)*a/(1-k);
   fplot(@(t) x1+R*cos(t), @(t) R*sin(t),[0,2*pi],'b')
end
plot(-a,0,'ro','markersize',4,'markerfacecolor','r') %hilos
plot(a,0,'bo','markersize',4,'markerfacecolor','b')
hold off
axis equal
grid on
xlabel('x')
ylabel('y');
title('Líneas de fuerza y equipotenciales')

Campo eléctrico producido por una esfera uniformemente cargada con una cavidad

Antes de resolver el problema, expresamos el campo eléctrico producido por una distribución eférica y uniforme de carga de forma vectorial

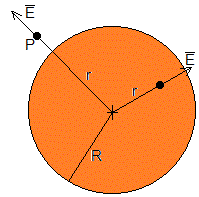
El campo eléctrico y el potencial producido por la distribución esférica y uniforme de carga en un punto P situado a una distancia r del centro, es

${\displaystyle \begin{array}{l}\overrightarrow{E}=\{\begin{array}{l}\frac{\rho }{3{\epsilon }_0}\overrightarrow{r},r<R\\ \frac{\rho }{3{\epsilon }_0}\frac{R^3}{r^3}\overrightarrow{r},r>R\end{array}\\ V(r)=\{\begin{array}{l}\frac{\rho }{6{\epsilon }_0}\left(3R^2-r^2\right),r<R\\ \frac{\rho }{3{\epsilon }_0}\frac{R^3}{r},r>R\end{array}\end{array}}$

Donde ρ en C/m³ es la densidad de carga, $\rho =\frac{Q}{\frac{4}{3}\pi R^3}$

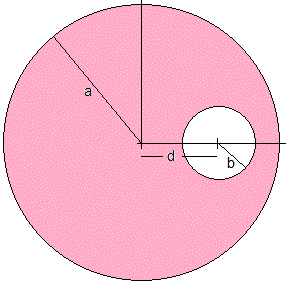
Sea una esfera de radio a uniformemente cargada con ρ C/m³ que contiene una cavidad de forma esférica de radio b. La distancia entre el centro de las esfera y el centro de la cavidad es d.

Vamos a utilizar el principio de superposición para calcular el campo eléctrico y el potencial en un punto P distante r del centro de la esfera cargada.

El campo eléctrico producido por la esfera con la cavidad es igual a la diferencia entre el campo eléctrico producido por una esfera de radio a en el punto P y el campo eléctrico producido por otra esfera de radio b en dicho punto, ambas esferas están uniformemente cargadas con densidad ρ.

Se estudian los tres casos posibles

• El punto P se encuentra dentro de la cavidad, r<a, r'<b
• El punto P se encuentra fuera de la cavidad, pero dentro de la esfera, r<a, r'>b
• El punto P se encuentra fuera de la esfera, r>a

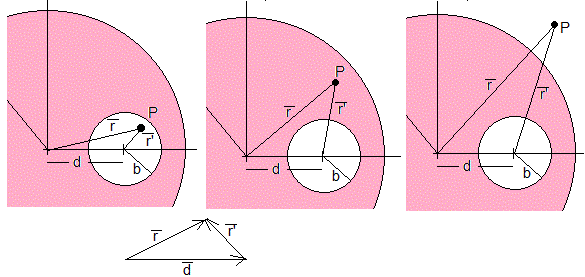
Siendo r la distancia del punto P al centro de la esfera y r' la distancia de dicho punto al centro de la cavidad. Relacionamos estas distancias

${\displaystyle \begin{array}{l}\overrightarrow{r}=\overrightarrow{r\text{'}}+\overrightarrow{d}\\ \overrightarrow{r\text{'}}=\overrightarrow{r}-\overrightarrow{d}\\ \overrightarrow{r\text{'}}·\overrightarrow{r\text{'}}=\left(\overrightarrow{r}-\overrightarrow{d}\right)·\left(\overrightarrow{r}-\overrightarrow{d}\right)\\ r{\text{'}}^2=r^2+d^2-2\overrightarrow{r}·\overrightarrow{d}\\ \overrightarrow{r}=x\widehat{i}+y\widehat{j},\overrightarrow{d}=d\widehat{i}\\ r{\text{'}}^2=x^2+y^2+d^2-2dx\end{array}}$

• El punto P se encuentra dentro de la cavidad, r<a, r'<b

${\displaystyle \begin{array}{l}\overrightarrow{E}=\frac{\rho }{3{\epsilon }_0}\overrightarrow{r}-\frac{\rho }{3{\epsilon }_0}\overrightarrow{r\text{'}}=\frac{\rho }{3{\epsilon }_0}\overrightarrow{d}\\ V=\frac{\rho }{6{\epsilon }_0}\left(3a^2-r^2\right)-\frac{\rho }{6{\epsilon }_0}\left(3b^2-r{\text{'}}^2\right)=\frac{\rho }{6{\epsilon }_0}\left(3\left(a^2-b^2\right)+r{\text{'}}^2-r^2\right)\end{array}}$

El campo eléctrico es constante en la cavidad

• El punto P se encuentra fuera de la cavidad, pero dentro de la esfera, r<a, r'>b

${\displaystyle \begin{array}{l}\overrightarrow{E}=\frac{\rho }{3{\epsilon }_0}\overrightarrow{r}-\frac{\rho }{3{\epsilon }_0}\frac{b^3}{r{\text{'}}^3}\overrightarrow{r\text{'}}=\frac{\rho }{3{\epsilon }_0}\left(\overrightarrow{r}-\frac{b^3}{{\left(r^2+d^2-2\overrightarrow{r·}\overrightarrow{d}\right)}^{3/2}}\left(\overrightarrow{r}-\overrightarrow{d}\right)\right)\\ V=\frac{\rho }{6{\epsilon }_0}\left(3a^2-r^2\right)-\frac{\rho }{3{\epsilon }_0}\frac{b^3}{r\text{'}}=\frac{\rho }{6{\epsilon }_0}\left(3a^2-r^2-2\frac{b^3}{r\text{'}}\right)\end{array}}$

• El punto P se encuentra fuera de la esfera, pero dentro de la esfera r>a

${\displaystyle \begin{array}{l}\overrightarrow{E}=\frac{\rho }{3{\epsilon }_0}\frac{a^3}{r^3}\overrightarrow{r}-\frac{\rho }{3{\epsilon }_0}\frac{b^3}{r{\text{'}}^3}\overrightarrow{r\text{'}}=\frac{\rho }{3{\epsilon }_0}\left(\frac{a^3}{r^3}\overrightarrow{r}-\frac{b^3}{{\left(r^2+d^2-2\overrightarrow{r·}\overrightarrow{d}\right)}^{3/2}}\left(\overrightarrow{r}-\overrightarrow{d}\right)\right)\\ V=\frac{\rho }{3{\epsilon }_0}\frac{a^3}{r}-\frac{\rho }{3{\epsilon }_0}\frac{b^3}{r\text{'}}=\frac{\rho }{6{\epsilon }_0}\left(2\frac{a^3}{r}-2\frac{b^3}{r\text{'}}\right)\end{array}}$

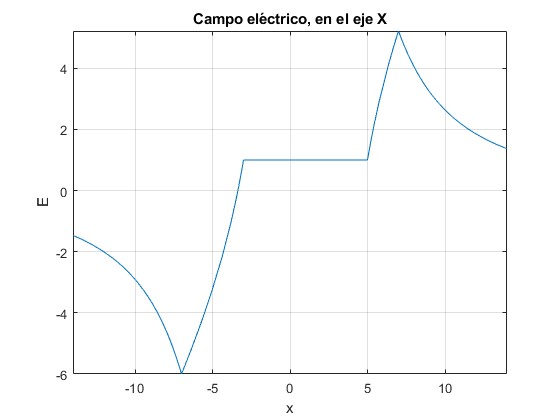
Representamos el campo eléctrico E/(ρ/3ε₀) a lo largo del eje X, con los siguientes datos: radio de la esfera a=7d, radio de la cavidad b=4d. Tomamos d como unidad de distancia

${\displaystyle \overrightarrow{d}=d\widehat{i},\overrightarrow{r}=x\widehat{i},\overrightarrow{r\text{'}}=(x-d)\widehat{i}}$

function esfera_hueca_1
    d=1; %centro del hueco
    a=7*d; %radio esfera
    b=4*d; %radio cavidad
    f=@(x) cElectrico(x);
    fplot(f ,[-2*a,2*a])
    grid on
    xlabel('x')
    ylabel('E')
    title('Campo eléctrico, en el eje X')

    function z=cElectrico(x)
        if abs(x)<a
            if x>d-b && x<d+b
                z=d;
            else
                z=x-b^3*sign(x-d)./(x-d).^2;
            end
        else
            z=a^3*sign(x)./x.^2-b^3*sign(x-d)./(x-d).^2;
        end
    end
end

Representamos las equipotenciales mediante la función contour de MATLAB. En color negro, línea gruesa, se muestra la esfera y la cavidad

d=1; %centro del hueco
a=7*d; %radio esfera
b=4*d; %radio cavidad
xx=-8:0.1:8;
n=length(xx);
[X,Y]=meshgrid(xx,xx);
Z=zeros(n,n);
for i=1:n
    for j=1:n
        r=sqrt(X(i,j)^2+Y(i,j)^2); %desde el punto P al origen
        rp=sqrt((X(i,j)-d)^2+Y(i,j)^2); %desde el punto P al centro del hueco
        if r<a
            if rp<b
                Z(i,j)=3*(a^2-b^2)+rp^2-r^2;
            else
                Z(i,j)=3*a^2-r^2-2*b^3/rp;
            end
        else
            Z(i,j)=2*a^3/r-2*b^3/rp;
        end
    end
end
hold on
fplot(@(t) a*cos(t), @(t) a*sin(t),[0,2*pi],'color','k','lineWidth',1.5) 
fplot(@(t) d+b*cos(t), @(t) b*sin(t),[0,2*pi],'color','k','lineWidth',1.5)
contour(X,Y,Z)
hold offaxis equal
xlabel('x')
ylabel('y')
title('Equipotenciales')

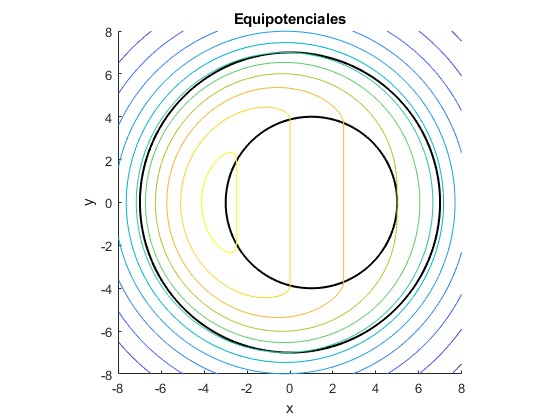
Observamos que las equipotenciales son casi circunferencias fuera de la esfera. El efecto de la cavidad se diluye un poco más allá del radio a de la esfera

Referencias

J. Pierrus. Solved Problems in Classical Electromagnetism. Analytical and numerical solutions with comments. Oxford University Press (2018). Question 2.7, pp. 61-64. Question 2.8, pp. 65-66