Equilibrio de cargas iguales situadas en una circunferencia
Equilibrio
Cuando ponemos n cargas en un circunferencia de radio R. En la configuración de equilibrio, las cargas se sitúan en los vértices de un poligono regular de n lados tal como vamos a comprobar en los siguientes ejemplos.
Sistema de n=2 cargas
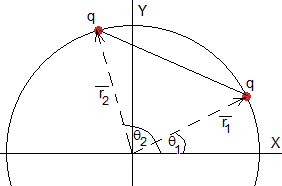
La posición angular de la primera carga es θ1 y de la segunda carga θ2
La energía eléctrostática del sistema de dos cargas es
Expresamos la energía U en términos de θ1 y θ2
En el equilibrio, la energía U deberá ser mínima
La solución es θ2-θ1=π. Como cabría esperar en el equilibrio, las cargas están situadas en los extremos de un diámetro de la circunferencia.
Sistema de n=3 cargas
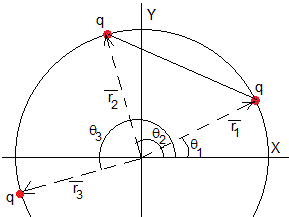
La posición angular de la primera carga es θ1, de la segunda carga θ2 y de la tercera θ3
La energía eléctrostática del sistema de tres cargas es
En el equilibrio, la energía U deberá ser mínima
La solución a este sistema es, θ2-θ1=θ, θ3-θ1=2θ, θ3-θ2=θ. Las tres ecuaciones se reducen a una única ecuación.
Llamando x=cos(θ/2), obtenemos la ecuación cúbica
>> roots([4,2,0,-1]) ans = -0.5000 + 0.5000i -0.5000 - 0.5000i 0.5000 + 0.0000i
La raíz real cúbica de esta ecuación es x=1/2, cos(θ/2)=1/2, θ=120°. Las cargas se sitúan en el vértice de un triángulo equilátero
Sistema de n=4 cargas
La posición angular de la primera carga es θ1, de la segunda carga θ2, de la tercera θ3 y de la cuarta θ4
La energía eléctrostática del sistema de cuatro cargas es
En el equilibrio la energía U deberá ser mínima
La solución a este sistema es, θ2-θ1=θ, θ3-θ2=θ, θ4-θ3=θ, θ4-θ2=2θ, θ4-θ1=3θ, θ3-θ1=2θ, θ4-θ2=2θ. Las cuatro ecuaciones se reducen a dos ecuaciones.
En el equilibrio, las cargas se sitúan en los vértices de un cuadrado
Sistema de n cargas
En general, en el equilibrio, las cargas se sitúan en los vértices de un polígono regular.
hold on n=5; %número de cargas fplot(@(t) cos(t),@(t) sin(t), [0,2*pi]) %circunferencia for i=0:n-1 plot(cos(i*2*pi/n),sin(i*2*pi/n),'o','markersize',4,'markeredgecolor', 'r','markerfacecolor','r') line([cos(i*2*pi/n),cos((i+1)*2*pi/n)],[sin(i*2*pi/n),sin((i+1)*2*pi/n)], 'lineStyle','--') end hold off axis square axis off
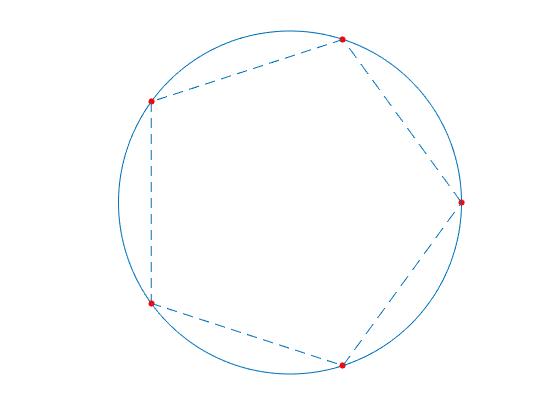
Resultante nula de las fuerzas sobre cada una de las partículas
Supongamos que tenemos n cargas iguales q situadas en los vértices de un polígono regular de n lados. Las partículas cargadas ejercen entre ellas fuerzas de repulsión. La resultante en la posición de equilibrio, tiene dirección radial. Si colocamos una carga Q de signo contrario en el centro del polígono ejercerá una fuerza de atracción sobre las partículas cargadas. En esta apartado, se calcula el valor de Q para que la resultante de las fuerzas que actúan sobre cada una de las partículas sea nula.
Vamos a estudiar varios ejemplos
Sistema de n=2 cargas
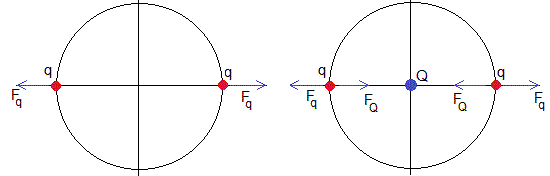
A la izquierda, en la situación de equilibrio, tenemos dos cargas iguales q en los extremos de un diámetro. Las cargas se repelen con una fuerza
Colocamos una carga Q de signo contrario en el centro de la circunferencia, que ejerce fuerzas de atraccción sobre cada una de las dos cargas q
La resultante de las fuerzas sobre cada una de las partículas es nula, cuando ambas fuerzas son iguales Fq=FQ
El resultado es Q=q/4.
Sistema de n=3 cargas
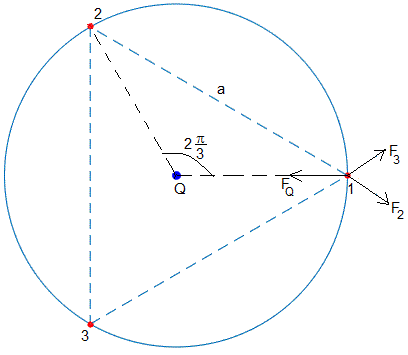
Longitud del lado a
Las fuerzas repulsivas que ejercen las cargas 1 y 3 sobre la carga 1
La resultante, Fp, es
La fuerza de atracción que ejerce la carga Q situada en el centro sobre la carga q considerada es
En el triángulo formado por el centro y las cargas 2 y 3 vemos que la longitud del lado a de un polígono regular de tres lados es, a=2Rsin(π/3).
El ángulo que forman los vectores y es π/3. La resultante tiene por módulo 2F2cos(π/6), su dirección radial
Para que se anulen ambas fuerzas, el valor de Q será
Sistema de n=4 cargas
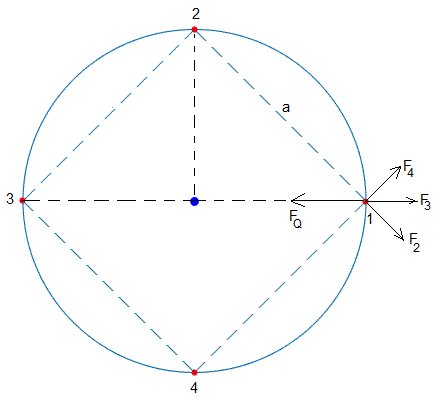
Longitud del lado a
Las fuerzas repulsivas que ejercen las cargas 2, y 4 sobre la carga 1 tienen por módulo
Las fuerza repulsiva que ejerce la carga 3 sobre la carga 1 es
La resultante, Fp, es la suma de dos contribuciones
La fuerza de atracción que ejerce la carga Q situada en el centro sobre la carga q considerada es
En el triángulo rectángulo formado por el centro y las cargas 1 y 2 vemos que la longitud del lado a de un polígono regular de cuatro lados es, .
El ángulo que forman los vectores y es π/2. La resultante tiene por módulo 2F2cos(π/4), su dirección radial
Para que se anulen ambas fuerzas, el valor de Q será
Sistema de n=5 cargas
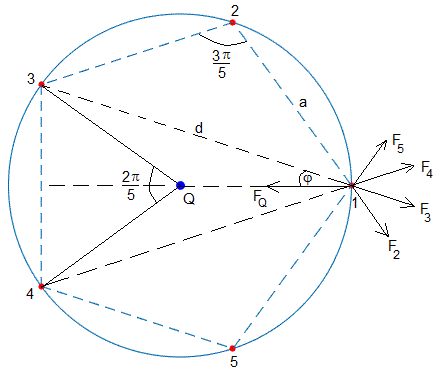
Longitud del lado a
Las fuerzas repulsivas que ejercen las cargas 2 y 5 sobre la carga 1
Las fuerzas repulsivas que ejercen las cargas 3 y 4 sobre la carga 1
En el triángulo formado por el centro y las cargas 3 y 4 vemos que la longitud del lado a de un polígono regular de cinco lados es a=2Rsin(π/5).
Los vectores y forman un ángulo de 3π/5. El módulo de la resultante de estas dos fuerzas es, 2F2cos(3π/10), su dirección radial
En el triángulo formado por las cargas 1, 2 y 3, la distancia entre las cargas 3 y 1 es d=2asin(3π/10)=4Rsin(π/5)sin(3π/10). El módulo de la fuerza vale
Los vectores y forman un ángulo de φ, tal que sinφ=(a/2)/d
>> asind(1/(4*sin(3*pi/10))) ans = 18
El módulo de la resultante de estas dos fuerzas es, 2F3cos(φ), su dirección radial
La resultante, Fp, es la suma de dos contribuciones
La fuerza de atracción que ejerce la carga Q situada en el centro sobre la carga q considerada es
Para que se anulen ambas fuerzas, el valor de Q será
Sistema de n=6 cargas
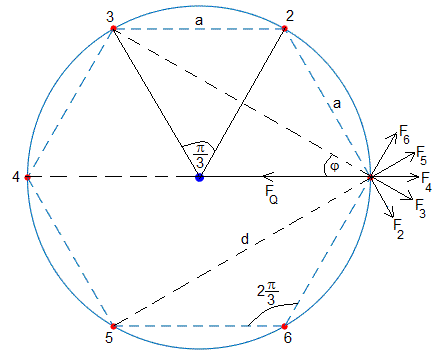
Longitud del lado a
Las fuerzas repulsivas que ejercen las cargas 2 y 6 sobre la carga 1
Las fuerzas repulsivas que ejercen las cargas 3 y 5 sobre la carga 1
Fuerza repulsiva que ejerce la carga 4 sobre la carga 1
La resultante, Fp, es la suma de tres contribuciones
La fuerza de atracción que ejerce la carga Q situada en el centro sobre la carga q considerada es
En el triángulo formado por el centro y las cargas 2 y 3 vemos que la longitud del lado a de un polígono regular de seis lados es a=2Rsin(π/6)=R.
Los vectores y forman un ángulo de 2π/3. El módulo de la resultante de estas dos fuerzas es, 2F2cos(π/3), su dirección radial
En el triángulo formado por las cargas 1, 5 y 6, la distancia entre las cargas 5 y 1 es d=2asin(π/3)=2Rsin(π/3). El módulo de la fuerza vale
Los vectores y forman un ángulo de 2φ. Sabiendo que las coordenadas de la carga 3 son (Rcos(2π/3), Rsin(2π/3))
La resultante en la dirección radial es 2F3cos(π/6)
Para que se anulen la ambas fuerzas, el valor de Q será
Sistema de n=7 cargas
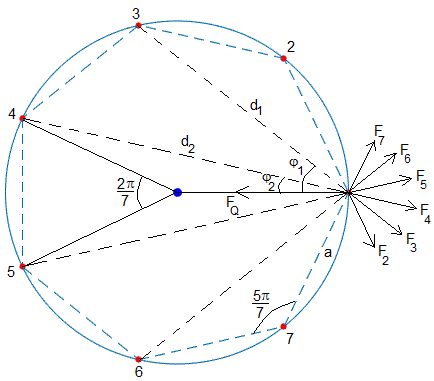
Longitud del lado a
Las fuerzas repulsivas que ejercen las cargas 2 y 7 sobre la carga 1
Las fuerzas repulsivas que ejercen las cargas 3 y 6 sobre la carga 1
Las fuerzas repulsivas que ejercen las cargas 4 y 5 sobre la carga 1
En el triángulo formado por el centro y las cargas 4 y 5 vemos que la longitud del lado a de un polígono regular de siete lados es, a=2Rsin(π/7).
Los vectores y forman un ángulo de 5π/7. El módulo de la resultante de estas dos fuerzas es, 2F2cos(5π/14), su dirección radial
En el triángulo formado por las cargas 1, 6 y 7, la distancia d1 entre las cargas 6 y 1 es d1=2asin(5π/14)=4Rsin(5π/14)sin(π/7). El módulo de la fuerza vale
Los vectores y forman un ángulo de 2φ1. Las coordendas de la carga 3 son (Rcos(4π/7), Rsin(4π/7)), por tanto,
La resultante en la dirección radial es 2F3cos(3π/14)
Las coordenadas de la carga 4 son (Rcos(6π/7), Rsin(6π/7)) y las coordenadas de 1 son (R,0), la distancia d2 es
El módulo de la fuerza es
Los vectores y forman un ángulo 2φ2, donde sinφ2=(a/2)/d2
>> asin(sin(pi/7)/(2*sin(3*pi/7))) ans = 0.2244 >> pi/14 ans = 0.2244
La resultante en la dirección radial es 2F4cos(φ)
La resultante, Fp, es la suma de tres contribuciones
La fuerza de atracción que ejerce la carga Q situada en el centro sobre la carga q considerada es
Para que se anulen la ambas fuerzas, el valor de Q será
Sistema de n=8 cargas
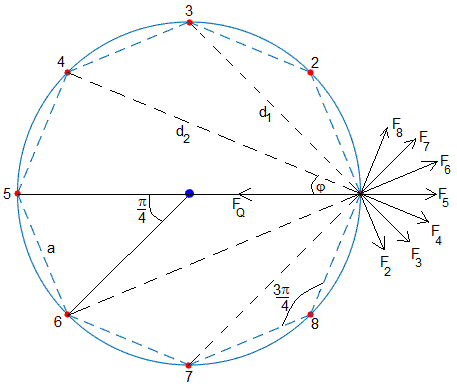
Longitud del lado a
Las fuerzas repulsivas que ejercen las cargas 2 y 8 sobre la carga 1
Las fuerzas repulsivas que ejercen las cargas 3 y 7 sobre la carga 1
Las fuerzas repulsivas que ejercen las cargas 4 y 6 sobre la carga 1
Fuerza repulsiva que ejerce la carga 5 sobre la carga 1
La resultante, Fp, es la suma de cuatro contribuciones
La fuerza de atracción que ejerce la carga Q situada en el centro sobre la carga q considerada es
En el triángulo formado por el centro y las cargas 5 y 6 vemos que la longitud del lado a de un polígono regular de ocho lados es, a=2Rsin(π/8).
Los vectores y forman un ángulo de 3π/4. El módulo de la resultante de estas dos fuerzas es, 2F2cos(3π/8), su dirección radial
Las coordenadas de la carga 3 son (Rcos(π/2), Rsin(π/2))=(0,R), las coordenadas de la carga 1 son (R,0), la distancia entre la carga 3 y 1 es . El módulo de la fuerza vale
Los vectores y forman un ángulo de π/2. La resultante en la dirección radial es 2F3cos(π/4),
Las coordenadas de la carga 4 son (Rcos(3π/4), Rsin(3π/4)) y las coordenadas de 1 son (R,0), la distancia d2 es
El módulo de la fuerza es
Los vectores y forman un ángulo 2φ, donde sinφ=(a/2)/d2
La resultante en la dirección radial es 2F4cos(φ)
Para que se anulen la ambas fuerzas, el valor de Q será
Sistema de n cargas
Para n impar, 3,5,7,9...
-
Para n par, 2, 4, 6, 8,...
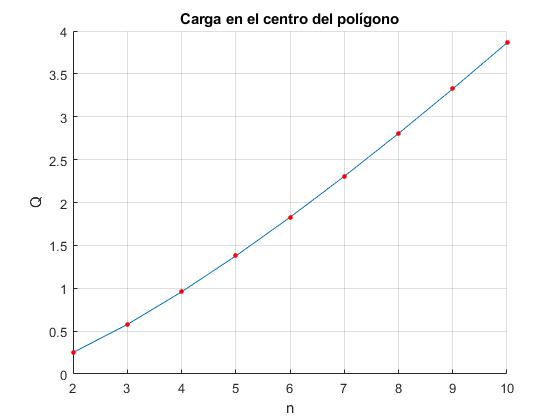
Representamos la carga en el centro Q/q en función del número n de cargas en la circunferencia de radio R
hold on
N=10;
Q=zeros(1,N-1);
Q(1)=1/4;
for n=3:N
if rem(n,2)==0
Q(n-1)=(1/2+sum(1./sin(pi*m/n)))/2;
else
m=1:(n-1)/2;
Q(n-1)=sum(1./sin(pi*m/n))/2;
end
end
plot(2:N,Q,'-o','markersize',3,'markeredgecolor','r','markerfacecolor','r')
xlabel('n')
ylabel('Q')
grid on
title('Carga en el centro del polígono')
Referencias
Norberto Helil Pasqua , Paulo Daniel Emmel. Cancelamento das Forças de Vínculo em Anel Condutor Carregado com nq Cargas por Meio de uma Carga Q de Sinal Contrário Posicionada no Centro.. Revista Brasileira de Ensino de Física, vol.23, no.2, Junho, 2001. https://www.scielo.br/j/rbef/i/2001.v23n2/

