El electroscopio

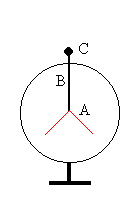
El electroscopio consta de dos láminas delgadas de oro o aluminio A que están fijas en el extremo de una varilla metálica B que pasa a través de un soporte C de ebonita, ámbar o azufre. Cuando se toca la bola del electroscopio con un cuerpo cargado, las hojas adquieren carga del mismo signo y se repelen siendo su divergencia una medida de la cantidad de carga que han recibido. La fuerza de repulsión electrostática se equilibra con el peso de las hojas.

Si se aplica una diferencia de potencial entre la bola C y la caja del mismo, las hojas también se separan. Se puede calibrar el electroscopio trazando la curva que nos da la diferencia de potencial en función del ángulo de divergencia.

Un modelo simplificado de electroscopio consiste en dos pequeñas esferas de masa m cargadas con cargas iguales q y del mismo signo que cuelgan de dos hilos de longitud l, tal como se indica la figura. A partir de la medida del ángulo θ que forma una bolita con la vertical, se calcula su carga q.

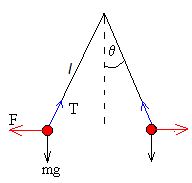
Sobre una bolita actúan tres fuerzas

El peso, mg
La tensión de la cuerda, T
La fuerza de repulsión eléctrica entre las bolitas, F

En el equilibrio

Tsinθ =F
Tcosθ =mg

Conocido el ángulo θ se determina la carga q

Dividiendo la primera ecuación entre la segunda, eliminamos la tensión T y obtenemos

F=mg·tanθ

Midiendo el ángulo θ obtenemos la fuerza de repulsión F entre las dos esferas cargadas

$F = \frac{1}{4 π ε_{0}} \frac{q^{2}}{{(2 l \sin θ)}^{2}}$

Calculamos el valor de la carga q, si se conoce la longitud l del hilo que sostiene las esferas cargadas.

Ejemplo:

Sea la masa m=50 g=0.05 kg, la longitud del hilo l=50 cm=0.5 m. Se ha medido el ángulo que hace los hilos con la vertical θ=22º, determinar la carga q de las bolitas.

La separación entre las cargas es x=2·0.5·sin(22º)=0.375 m

La fuerza F de repulsión entre las cargas vale

$F = 9 \cdot 10^{9} \frac{q^{2}}{{0.375}^{2}}$

De las ecuaciones de equilibrio

Tsin22º=F
Tcos22º=0.05·9.8

eliminamos T y despejamos la carga q, se obtiene 1.76·10^-6 C ó 1.76 μC.

Conocida la carga q se determina el ángulo θ

Eliminado T en las ecuaciones de equilibrio, obtenemos la ecuación

$\sin^{3} θ = q^{2} k \cos θ k = \frac{9}{4 l^{2} m g}$

La carga q está en μC y la masa m de la bolita en g.

Expresando el coseno en función del seno, llegamos a la siguiente ecuación cúbica

$x^{3} + (x - 1) k^{2} q^{4} = 0 x = \sin^{2} θ$

El script de MATLAB, calcula la raíz real de la ecuación cúbica

longitud=0.5;  %longitud del péndulo en metros
m=50; %gramos
k=9.0/(4*longitud*longitud*m*9.8); 
q=1.76;  %micro coulombios
%raíz real de la ecuación cúbica x^3+a*x^2+b*x+c=0
a=0;
b=q^4*k^2;
c=-b;
Q=(a^2-3*b)/9;
R=(2*a^3-9*a*b+27*c)/54;
A=-sign(R)*nthroot(abs(R)+sqrt(R^2-Q^3),3);
B=Q/A;
x=(A+B)-a/3;
%ángulo en grados
angulo=asin(sqrt(x))*180/pi

angulo =   22.0255

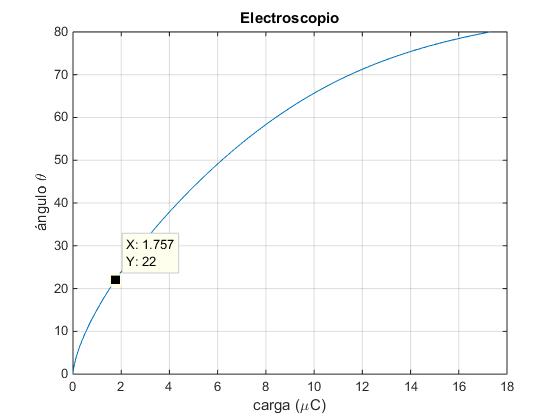
En la figura, se muestra el comportamiento de un electroscopio, para cada carga q en μC tenemos un ángulo de desviación θ en grados, del hilo respecto de la vertical. Si se mide el ángulo θ en el eje vertical obtenemos la carga q en el eje horizontal.

Representamos la función

$q = \sqrt{\frac{\sin^{3} θ}{k \cos θ}}$

Cambiamos los ejes de modo que en el eje horizontal ponemos la carga q y en el eje vertical su correspondiente ángulo θ de desviación en grados

longitud=0.5;  %longitud del péndulo en metros
m=50; %gramos
k=9.0/(4*longitud*longitud*m*9.8);
ang=0:pi/360:4*pi/9; %ángulos
x=sqrt(sin(ang).^3./(k*cos(ang))); %cargas 
plot(x,ang*180/pi)
grid on
xlabel('carga (\muC)')
ylabel('ángulo \theta')
title('Electroscopio')

Pérdidas de carga

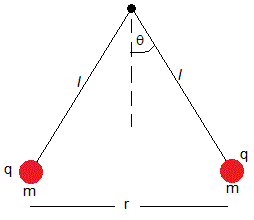
Dos bolitas de masa m cuelgan de hilos inextensibles y de masa despreciable de longitud l. Están inicialmente cargadas con una carga positiva q₀. El ángulo inicial de equilibrio es θ₀, o la separación inicial r₀=2dsinθ₀.

La carga de cada bolita disminuye con el tiempo de la forma, $q = q_{0} {(1 - b t)}^{3 / 2}$ , donde b es una constante dada. Como consecuencia, las bolas se van aproximando. Vamos a determinar el ángulo θ o la separación r en función del tiempo.

Dibujamos las fuerzas sobre cada bolita y sus componentes en la dirección tangencial

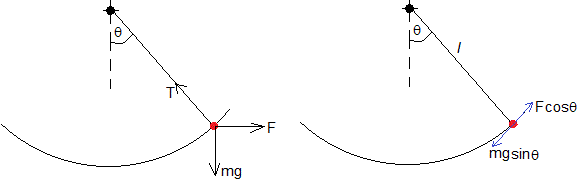
La ecuación del movimiento en la dirección tangencial es

$\begin{array}{l} m l \frac{d^{2} θ}{d t^{2}} = \frac{1}{4 π ε_{0}} \frac{q^{2}}{r^{2}} \cos θ - m g \sin θ \\ m l \frac{d^{2} θ}{d t^{2}} = \frac{1}{4 π ε_{0}} \frac{q_{0}^{2} {(1 - b t)}^{3}}{4 l^{2} \sin^{2} θ} \cos θ - m g \sin θ \\ \frac{d^{2} θ}{d t^{2}} = \frac{1}{4 π ε_{0}} \frac{q_{0}^{2} {(1 - b t)}^{3}}{4 m l^{3} \sin^{2} θ} \cos θ - \frac{g}{l} \sin θ \end{array}$

Ejemplo

Carga, q₀=7 μC
Longitud del péndulo, l=50 cm
Masa, m=50 g
Coeficiente de pérdida de carga, b=0.1 s^-1

Conocida la carga q₀ se determina el ángulo θ₀ de equilibrio

La bolita pierde su carga en el instante t=1/b

Se resuelve la ecuación diferencial por procedimientos numéricos en el intervalo de tiempo (0, 1/b), con las siguientes condiciones iniciales: en el instante t=0, la bolita parte en reposo de la posición angular θ=θ₀

q0=7; %carga inicial micro_C
m=50; %masa en gramos
longitud=0.5; %longitud en m
    
k=9.0/(4*longitud*longitud*m*9.8); 
%raíz real de la ecuación cúbica x^3+a*x^2+b*x+c=0
a=0;
b=q0^4*k^2;
c=-b;
Q=(a^2-3*b)/9;
R=(2*a^3-9*a*b+27*c)/54;
A=-sign(R)*nthroot(abs(R)+sqrt(R^2-Q^3),3);
B=Q/A;
x=(A+B)-a/3;
%ángulo inicial 
angulo=asin(sqrt(x));
disp(angulo*180/pi)
    
b=0.1; %pérdidas
f=@(t,x) [x(2);	9*(1-b*t)^3*q0^2*cos(x(1))/(4*m*longitud^3*sin(x(1))^2)
-9.8*sin(x(1))/longitud]; 
[t,x]=ode45(f,[0,1/b],[angulo,0]);
plot(t,x(:,1)*180/pi) %posición angular - tiempo
grid on
xlabel('t')
ylabel('\theta')
title('Electroscopio')

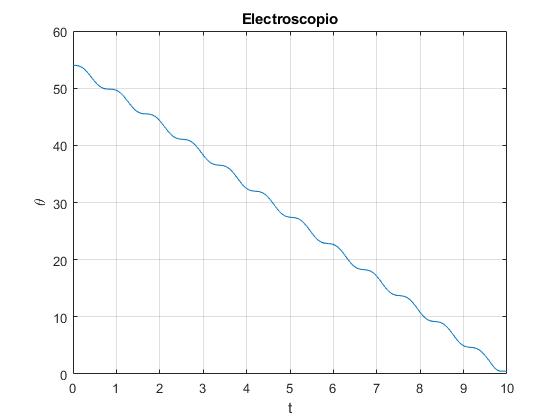
El ángulo inicial de equilibrio es θ₀=54°. La bolita pierde su carga en el instante t=10 s, la posición angular del péndulo es 0.4760°

53.9847
>> x(end,1)*180/pi
ans =    0.4760

A partir de esta posición, el péndulo se mueve hacia el origen, θ=0, bajo la acción de la componente tangencial del peso

Aproximación

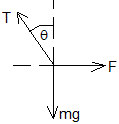
Cuando la descarga de las bolitas es muy lenta, la aceleración es aproximadamente nula, la bolita está en cada instante en equilibrio

${\begin{cases} T \cos θ = m g \\ T \sin θ = \frac{1}{4 π ε_{0}} \frac{q_{0}^{2} {(1 - b t)}^{3}}{r^{2}} \end{cases}$

Eliminamos la tensión T. Para ángulo pequeños tanθ≈sinθ

$\begin{array}{l} m g \tan θ = \frac{1}{4 π ε_{0}} \frac{q_{0}^{2} {(1 - b t)}^{3}}{r^{2}} \\ m g \frac{r}{2 l} \approx \frac{1}{4 π ε_{0}} \frac{q_{0}^{2} {(1 - b t)}^{3}}{r^{2}} \\ r = {(\frac{2 l}{4 π ε_{0}} \frac{q_{0}^{2}}{m g})}^{1 / 3} (1 - b t) \end{array}$

La velocidad de aproximación, dr/dt

$\frac{d r}{d t} = - b {(\frac{2 l}{4 π ε_{0}} \frac{q_{0}^{2}}{m g})}^{1 / 3}$

Representamos la velociad angular dθ/dt del péndulo en función del tiempo. Sustituyendo en el script las siguientes líneas de código

...
plot(t,x(:,2)) %velocidad - tiempo
v=-b*(18*longitud*q0^2/(9.8*m))^(1/3); %velocidad 'media'
line([0,1/b],[v,v],'color','r')
...

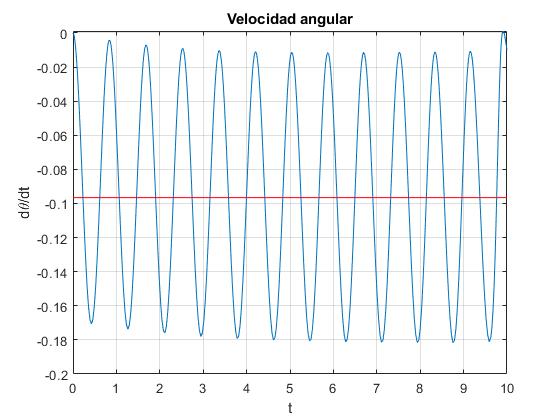
Vemos que la velocidad angular de aproximación no es constante, hay momentos en los que el péndulo casi se detiene, como apreciamos en la simulación más abajo. La línea horizontal representa, la velocidad de aproximación 'media', calculada suponiendo que el péndulo permanece en equilibrio en cada instante

Actividades

El programa interactivo genera aleatoriamente una carga q₀ medida en μC, cada vez que se pulsa el botón titulado Nuevo.

A partir de la medida de su ángulo de desviación θ₀, en la escala graduada angular, se puede calcular la carga q₀ de la bolita resolviendo las dos ecuaciones de equilibrio .

Se introduce

El valor de la masa m en gramos de la bolita, en el control titulado Masa.
El valor del coeficiente de pérdida de carga b s^-1 de la bolita, en el control titulado Pérdida de carga. El valor introducido se divide entre 100
La longitud del hilo está fijado l=50 cm.

Cuando se pulsa el botón titulado ►, las bolitas empiezan a perder carga y se aproximan una a la otra.

Cuando han perdido toda la carga, las bolitas se siguen aproximando ya que sigue actuando la componente tangencial del peso. El movimiento se detiene cuando las bolitas descargadas llegan a la posición de equilibrio estable θ=0

En la parte superior izquierda, se proporcionan los datos de

el tiempo, t
la posición angular, θ en grados
la velocidad angular, dθ/dt
la carga, q de la bolita en μC

Pérdida de carga (×0.01):
Masa (g):

Repulsión de dos partículas cargadas

Consideremos ahora, que las bolitas, suspendidas cada una de un hilo de longitud L tienen distinta carga q₁ y q₂, ambas del mismo signo y distinta masa m₁ y m₂.

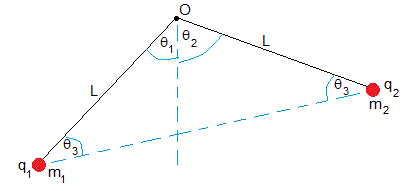
Las bolitas se repelen y forman ángulos θ₁ y θ₂ con la vertical, tal como se indica en la figura.

En la situación de equilibrio, las dos bolitas y el punto O de suspensión forman un triángulo isósceles, cuyo vértice forma un ángulo θ₁+θ₂ y la línea que une las bolitas forma con cada hilo un ángulo θ₃. Como los ángulo interiores de un triángulo suman 180 grados

$θ_{3} = \frac{π}{2} - \frac{θ_{1} + θ_{2}}{2}$

La separación de equilibrio entre las bolitas es 2Lcosθ₃

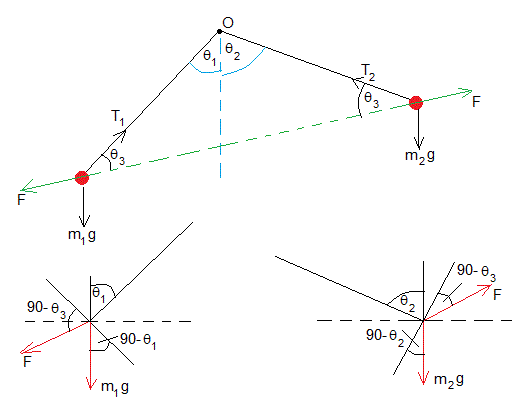
Las fuerzas sobre la bolita izquierda de masa m₁ y carga q₁ son:

El peso, m₁g
La tensión del hilo, T₁
La fuerza de repulsión F

$F = \frac{1}{4 π ε_{0}} \frac{q_{1} q_{2}}{4 L^{2} \cos^{2} θ_{3}}$

Las fuerzas sobre la bolita derecha de masa m₂ y carga q₂ son:

El peso, m₂g
La tensión del hilo, T₂
La fuerza de repulsión F, igual y de sentido contrario

No estamos interesados en las tensiones T₁ y T₂ de los hilos, por lo que proyectamos los pesos y las fuerzas de repulsión a lo largo de las direcciones perpendiculares a cada uno de los hilos, tal como se aprecia en la figura.

La condición de equilibrio en dicha dirección para la bolita izquierda, se escribe

m₁gcos(90-θ₁)=F·cos(90-θ₃)

y de modo análogo, para la bolita derecha

m₂gcos(90-θ₂)=F·cos(90-θ₃)

El sistema de dos ecuaciones con dos incógnitas, θ₁ y θ₂, se escribe

${\begin{cases} m_{1} g \sin θ_{1} = \frac{1}{4 π ε_{0}} \frac{q_{1} q_{2}}{4 L^{2} \sin^{2} ((θ_{1} + θ_{2}) / 2)} \cos \frac{θ_{1} + θ_{2}}{2} \\ m_{2} g \sin θ_{2} = \frac{1}{4 π ε_{0}} \frac{q_{1} q_{2}}{4 L^{2} \sin^{2} ((θ_{1} + θ_{2}) / 2)} \cos \frac{θ_{1} + θ_{2}}{2} \end{cases}$

Definimos los parámetros adimensionales m=m₁/m₂ y

$k = \frac{1}{4 π ε_{0}} \frac{q_{1} q_{2}}{4 L^{2} m_{1} g}$

El sistema de dos ecuaciones se reduce a otro más simple

${\begin{cases} \sin θ_{1} = k \cos \frac{θ_{1} + θ_{2}}{2} \sin^{- 2} \frac{θ_{1} + θ_{2}}{2} \\ \sin θ_{2} = m \sin θ_{1} \end{cases}$

m=1.3;
k=0.275;
x0=[pi/6,pi/3];
g=@(x) [sin(x(1))-k*cos((x(2)+x(1))/2)/(sin((x(2)+x(1))/2)^2),
sin(x(2))-m*sin(x(1))];
[x,fval]=fsolve(g,x0);
x*180/pi

ans =   32.8858   44.8987

Los ángulos de equilibrio que forman los hilos con la vertical para los valores de los parámetros adimensionales m=1.3 y k=0.275, son: θ₁=32.9° y θ₂=44.9°

Estabilidad de la solución

Vamos a comprobar que los ángulos de equilibrio calculados, corresponden a una situación de equilibrio estable, es decir, la energía potencial presenta un mínimo

La energía de este sistema de dos partículas interactuantes es igual a la suma de la energía potencial correspondiente al peso de cada bolita y la energía de interacción eléctrica

Establecemos el origen de la energía potencial gravitatoria en la posición en que se encuentran las bolitas descargadas, L por debajo del vértice O. Cuando una bolita se desplaza θ₁ se eleva L(1-cosθ₁) y su energía potencial se incrementa en m₁gL(1-cosθ₁). La energía potencial de la segunda bolita cuando se desplaza θ₂, es m₂gL(1-cosθ₂)

El nivel cero de la energía potencial correspondiente a la interacción eléctrica está en el infinito.

Cuando las cargas están separadas una distancia 2Lcosθ₃, la energía potencial total es

$\begin{array}{l} U (θ_{1}, θ_{2}) = m_{1} g L (1 - \cos θ_{1}) + m_{2} g L (1 - \cos θ_{2}) + \frac{1}{4 π ε_{0}} \frac{q_{1} q_{2}}{2 L \cos θ_{3}} \\ u (θ_{1}, θ_{2}) = m (1 - \cos θ_{1}) + (1 - \cos θ_{2}) + 2 m k \sin^{- 1} (\frac{θ_{1} + θ_{2}}{2}) \end{array}$

Con sinθ₂=m·sinθ₁

m=1.3;
k=0.275;
x0=[pi/6,pi/3];
g=@(x) [sin(x(1))-k*cos((x(2)+x(1))/2)/(sin((x(2)+x(1))/2)^2),
sin(x(2))-m*sin(x(1))];
[x,fval]=fsolve(g,x0);
 
%representa la energía potencial en un intervalo de 10º alrededor del
%mínimo
fi_1=x(1)-pi/18:0.1*pi/180:x(1)+pi/18;
fi_2=asin(m*sin(fi_1));
u=m*(1-cos(fi_1))+(1-cos(fi_2))+2*m*k./sin((fi_1+fi_2)/2);
plot(fi_1*180/pi,u)
grid on
xlabel('\theta')
ylabel('u(\theta)')
title('Energía potencial')

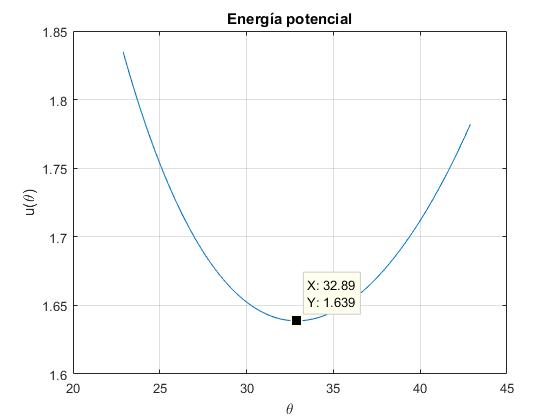
La energía potencial reducida u(θ₁) presenta un mínimo en θ₁=32.9° por tanto, se trata de una posición de equilibrio estable

Fijando m=2, trazamos la gráfica θ₁ y θ₂ según vamos incrementando el parámetro k de 0 a 2, es decir la fuerza de repulsión F o las cargas de las partículas.

m=2;
x0=[pi/6,pi/3];
ang=zeros(2,201);
i=0;
for k=0:0.01:2;
    g=@(x) [sin(x(1))-k*cos((x(2)+x(1))/2)/(sin((x(2)+x(1))/2)^2),
sin(x(2))-m*sin(x(1))];
    [x,fval]=fsolve(g,x0);
    i=i+1;
    ang(1,i)=x(1)*180/pi;
    ang(2,i)=x(2)*180/pi;
end
plot(0:0.01:2,ang(1,:),'r',0:0.01:2,ang(2,:),'b');
grid on
xlabel('f')
ylabel('\theta_1, \theta_2')
title('Angulos de equilibrio')

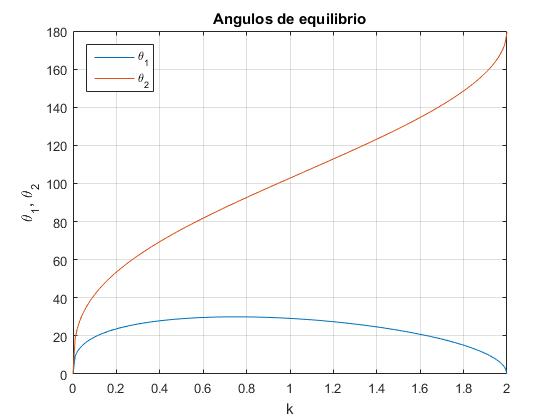
Como vemos en la gráfica, para m>1 a medida que k crece el ángulo θ₂ alcanza los 90°, entonces de la segunda ecuación θ₁=asin(1/m). Introducimos este valor en la primera ecuación y despejamos k

${\begin{cases} θ_{2} = \frac{π}{2} \sin θ_{1} = \frac{1}{m} \\ \sin^{2} \frac{θ_{1} + θ_{2}}{2} \sin θ_{1} = k \cos \frac{θ_{1} + θ_{2}}{2} \end{cases}$

Desarrollando, el seno y coseno de la suma de dos ángulos y elevando al cuadrado, despejamos k

$k = \frac{m + 1}{m \sqrt{2 m (m - 1)}}$

Para m=2, el segundo hilo se desvía θ₂=90° y el primero, θ₁=30° para k=3/4. Al aumentar k, θ₁ decrece a cero y θ₂ crece hasta el valor de 180° cuando se alcanza un valor máximo de k=2.

Las bolitas tiene la misma masa y carga

Consideremos de nuevo, el caso en el que las bolitas tienen la misma carga q₁=q₂=q, ambas del mismo signo y la misma masa m₁=m₂=m.

Entonces, θ₁=θ₂=θ, θ₃=π/2-θ. La condición de equilibrio, se escribe

$m g \sin θ = \frac{1}{4 π ε_{0}} \frac{q^{2}}{4 L^{2} \sin^{2} θ} \cos θ$

En términos del parámetro adimensional k

$\begin{array}{l} \sin^{3} θ = k \cdot \cos θ k = \frac{1}{4 π ε_{0}} \frac{q^{2}}{4 L^{2} m g} \\ x^{3} + k^{2} x - k^{2} = 0 x = \sin^{2} θ \end{array}$

Obtenemos una ecuación cúbica en x=sin²θ

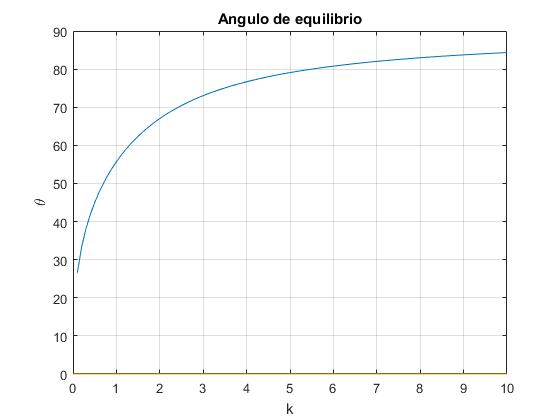
Calculamos y rerpesentamos los ángulos de equilibrio θ a medida que incrementamos el parámetro k, la carga q de las partículas. El ángulo θ tiende hacia 90°

k=0:0.1:10;
%raíz real de la ecuación cúbica x^3+a*x^2+b*x+c=0
a=0;
b=k.^2;
c=-b;
Q=(a^2-3*b)/9;
R=(2*a^3-9*a*b+27*c)/54;
A=-sign(R).*nthroot(abs(R)+sqrt(R.^2-Q.^3),3);
B=Q./A;
ang=asin(sqrt(A+B-a/3));
plot(k,ang*180/pi);
grid on
xlabel('k')
ylabel('\theta')
title('Angulo de equilibrio')

Referencias

Physics Challenges for Teachers and Students. A Slow Approach. The Physics Teacher. Vol. 42, February 2004. pp. 124

Carl E Mungan. Electrostatic repulsion of charged pith balls hanging from strings. Eur. J. Phys. 32 (2011) 207-212.

Este artículo está disponible en la dirección: https://www.usna.edu/Users/physics/mungan/Publications/Publications.php#fndtn-panel120162017