Sistema formado por dos cargas puntuales

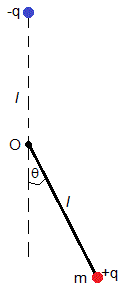
Una varilla de longitud l y masa despreciable, está sujeta por un extremo en O y en el otro extremo, está unida a una partícula de masa m y carga +q. La otra carga -q está sujeta una distancia l por encima de O.

Cuando θ es el ángulo que forma la varilla con la vertical

• La energía potencial gravitatoria es -mglcosθ tomando como referencia el punto O de suspensión de la varilla

• La energía potencial electrostática es

${\displaystyle -\frac{1}{4\pi {\epsilon }_0}\frac{q^2}{d}=-\frac{1}{4\pi {\epsilon }_0}\frac{q^2}{2l\cos \frac{\theta }{2}}}$

La energía potencial total es

${\displaystyle \begin{array}{l}{E}_p(\theta )=-mgl\cos \theta -\frac{1}{4\pi {\epsilon }_0}\frac{q^2}{2l\cos \frac{\theta }{2}}\\ e_p(\theta )=-\cos \theta -\frac{k}{\cos \frac{\theta }{2}},k=\frac{\frac{1}{4\pi {\epsilon }_0}\frac{q^2}{2l}}{mgl}\end{array}}$

k es el cociente de las energías potenciales cuando θ=0.

Representamos la energía potencial e_p(θ) en unidades mgl, para θ≥0, ya que la función es simétrica

k=0.01;
f=@(x) -cos(x)-k./cos(x/2);
fplot(f,[0,pi])
th=2*acos((k/4)^(1/3));
line([th,th],[-1,f(th)], 'lineStyle','--')
set(gca,'XTick',0:pi/6:pi)
set(gca,'XTickLabel',{'0','\pi/6','\pi/3','\pi/2','2\pi/3','5\pi/6','\pi'})
xlabel('\theta')
ylabel('e_p(\theta)')
ylim([-1.1,1])
grid on
title('Energía potencial')

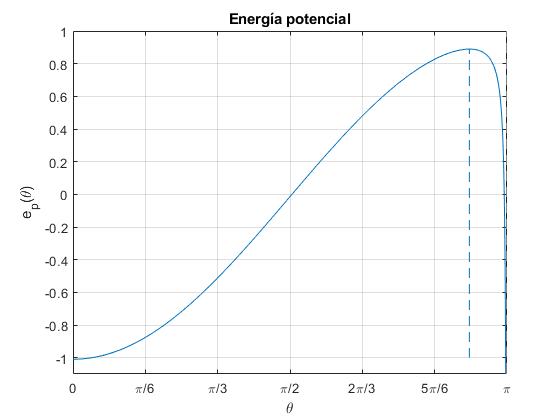
>> th*180/pi
ans =  164.3994

Vemos que tiene un mínimo en θ=0 (equilibrio estable) y un máximo (equilibrio inestable) para el ángulo θ_m que vamos a calcular

Derivamos e_p(θ) con respecto de θ e igualamos a cero

${\displaystyle \sin \theta -\frac{k}{2}\frac{\sin \frac{\theta }{2}}{{\cos }^2\frac{\theta }{2}}=\mathrm{0,}\{\begin{array}{l}\sin \frac{\theta }{2}=\mathrm{0,}{\theta }_m=0\\ {\cos }^3\frac{\theta }{2}=\frac{k}{4},{\theta }_m=2\arccos \left(\sqrt[3]{\frac{k}{4}}\right)\end{array}}$

Oscilaciones

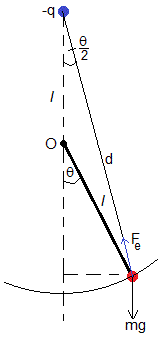
Analizamos las oscilaciones alrededor de la posición de equilibrio estable, θ=0

Las fuerzas que actúan sobre la partícula de masa m y carga +q son

• El peso, mg
• La fuerza de atracción, F_e

Calculamos las componentes tangenciales del peso y de la fuerza de atracción entre las cargas. La ecuación del movimiento en la dirección tangencial es

${\displaystyle \begin{array}{l}ml\frac{d^2\theta }{d{t}^2}=-mg\sin \theta +\frac{1}{4\pi {\epsilon }_0}\frac{q^2}{d^2}\sin \frac{\theta }{2}\\ ml\frac{d^2\theta }{d{t}^2}=-mg\sin \theta +\frac{1}{4\pi {\epsilon }_0}\frac{q^2}{4l^2{\cos }^2\frac{\theta }{2}}\sin \frac{\theta }{2}\\ \frac{d^2\theta }{d{t}^2}=-\frac{g}{l}\sin \theta +\frac{g}{l}\frac{k}{2}\frac{\sin \frac{\theta }{2}}{{\cos }^2\frac{\theta }{2}}\end{array}}$

La aceleración es nula en las posiciones de equilibrio, estable θ=0 e inestable θ=θ_m

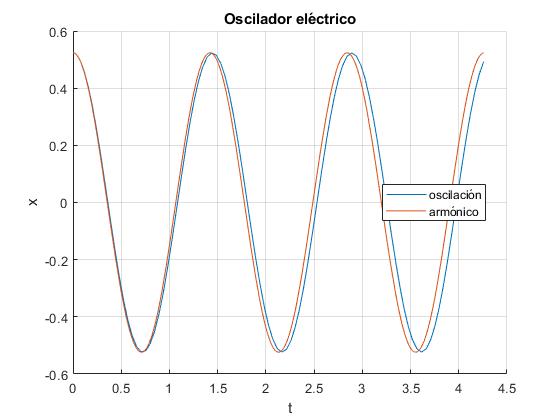
Resolvemos la ecuación diferencial para k=0.01, con la condición inicial en el instante t=0, θ=π/6, dθ/dt=0 (parte del reposo desde la posición 30°).

k=0.01;
l=0.5;
P=2*pi*sqrt(l/9.8); %periodo del péndulo simple
f=@(t,x) [x(2);-9.8*sin(x(1))/l+9.8*k*sin(x(1)/2)/(2*l*cos(x(1)/2)^2)]; 
[t,x]=ode45(f,[0,3*P],[pi/6,0]);
hold on
plot(t,x(:,1))
w=sqrt(9.8*(1-k/4)/l);
fplot(@(t) pi*cos(w*t)/6,[0,3*P])
hold off
grid on
xlabel('t')
legend('oscilación','armónico','Location','best')
ylabel('x');
title('Oscilador eléctrico')

Cuando la amplitud es pequeña, θ≈0, sin(θ/2)≈θ/2, cos(θ/2)≈1

${\displaystyle \begin{array}{l}\frac{d^2\theta }{d{t}^2}+\frac{g}{l}\left(1-\frac{k}{4}\right)\theta =0\\ {\omega }^2=\frac{g}{l}\left(1-\frac{k}{4}\right)\end{array}}$

Es la ecuación diferencial de un Movimiento Armónico Simple de frecuencia angular ω

En la gráfica, comparamos la solución numérica de la ecuación diferencial con el movimiento armónico simple θ=(π/6)cos(ωt), que parte t=0 desde la posición π/6 (30°) en reposo

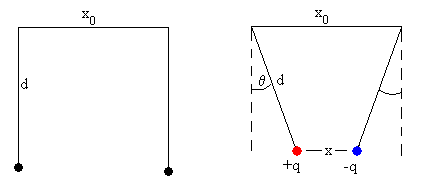
Sistema formado por dos cargas puntuales que cuelgan de hilos inextensibles

Dos partículas idénticas cargadas de masa m con cargas q iguales y opuestas se cuelgan de dos hilos inextensibles de longitud d separados inicialmente x₀

Normalmente, la separación de las cargas x es una función continua de la carga de las partículas, q. Al aumentar la carga la separación disminuye. Sin embargo, para cierto valor de la carga q_c de las partículas el sistema experimentan una transición discontinua a un nuevo estado de equilibrio en el que la separación x=0.

Equilibrio

Las cargas de distinto signo se atraen, acercándose a una distancia x. Los hilos forman un ángulo θ con la vertical.

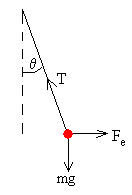
Las fuerzas sobre cada una de las partículas son:

• La fuerza que ejerce el hilo, es decir, la tensión del hilo, T

• La fuerza de atracción eléctrica, $F_e=\frac{1}{4\pi {\epsilon }_0}\frac{q·q}{x^2}$

• El peso, mg

En el equilibrio

${\displaystyle T\sin \theta =\frac{1}{4\pi {\epsilon }_0}\frac{q^2}{x^2}T\cos \theta =mg}$

Dividiendo las dos ecuaciones eliminamos la tensión T del hilo

${\displaystyle \tan \theta =\frac{1}{4\pi {\epsilon }_{0}mg}\frac{q^2}{x^2}}$

El ángulo θ está relacionado con la separación x entre las partículas, véase la primera figura

${\displaystyle \sin \theta =\frac{x_0-x}{2d}}$

Calculamos la separación de equilibrio x, hallando la raíz de la ecuación

${\displaystyle \frac{x_0-x}{\sqrt{4d^2-{(x_0-x)}^2}}=\frac{1}{4\pi {\epsilon }_{0}mg}\frac{q^2}{x^2}}$

Estabilidad

Energía potencial del sistema formado por las dos cargas es la suma de la energía potencial gravitatoria, las cargas se elevan d-d·cosθ, y la energía potencial electrostática, que es negativa por ser la fuerza atractiva.

${\displaystyle \begin{array}{l}{E}_p=2mg(d-d\cos \theta )-\frac{1}{4\pi {\epsilon }_0}\frac{q^2}{x}\\ E_p=4mgd{\sin }^2\left(\frac{\theta }{2}\right)-\frac{1}{4\pi {\epsilon }_0}\frac{q^2}{x}\end{array}}$

La posición de equilibrio es estable si la energía potencial es mínima en dicha posición, y es inestable si la energía potencial es máxima.

El signo de la derivada segunda de la energía potencial E_p(x) determina si la posición de equilibrio es estable (si es mayor que cero) o inestable (si es menor que cero).

Aproximaciones

Cuando d>>x₀, el ángulo θ es muy pequeño, hacemos las siguientes aproximaciones que simplifican notablemente los cálculos, tanθ≈sinθ≈θ

La ecuación que calcula la separación de equilibrio x se convierte en

${\displaystyle \frac{x_0-x}{2d}\approx \frac{1}{4\pi {\epsilon }_{0}mg}\frac{q^2}{x^2}}$

Tenemos que calcular las raíces de una ecuación cúbica

${\displaystyle x^3-x_0{x}^2+\frac{d{q}^2}{2\pi {\epsilon }_{0}mg}=0}$

La energía potencial se aproxima a

${\displaystyle E_p(x)=mg\frac{{(x_0-x)}^2}{4d}-\frac{1}{4\pi {\epsilon }_0}\frac{q^2}{x}}$

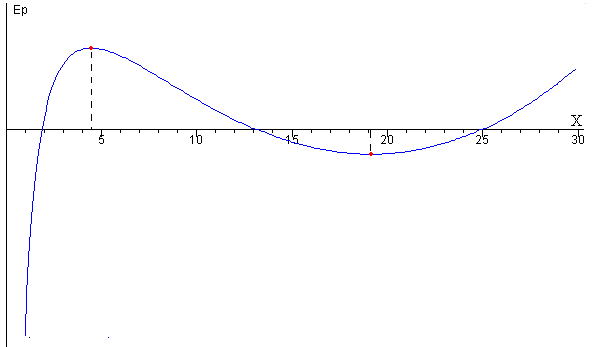
A medida que se aumenta la carga q de las partículas, el máximo y el mínimo se acercan, para un cierto valor de la carga q_c coinciden en el punto de inflexión

${\displaystyle \frac{d^2{E}_p(x)}{d{x}^2}=\frac{mg}{2d}-\frac{1}{2\pi {\epsilon }_0}\frac{q_c^2}{x^3}=0}$

Despejamos x y lo introducimos en la ecuación cúbica que nos proporciona las posiciones de equilibrio

${\displaystyle \begin{array}{l}{x}^3=\frac{q_c^{2}d}{\pi {\epsilon }_{0}mg}\\ \frac{q_c^{2}d}{\pi {\epsilon }_{0}mg}-x_0{\left(\frac{q_c^{2}d}{\pi {\epsilon }_{0}mg}\right)}^{2/3}+\frac{q_c^{2}d}{2\pi {\epsilon }_{0}mg}=0\\ q_c=\frac{2x_0}{3}\sqrt{\frac{2\pi x_0{\epsilon }_{0}mg}{3d}}\end{array}}$

Si la carga de las partículas q>q_c las dos partículas se juntan x=0.

Ejemplo:

• Masa de las partículas m=0.001 kg

• Carga de las partículas q=13·10^-9 C

• Longitud del hilo d=1.0 m

• Separación entre las partículas no cargadas x₀=0.2 m

Las raíces de la ecuación cúbica

${\displaystyle x^3-x_0{x}^2+\frac{d{q}^2}{2\pi {\epsilon }_{0}mg}=0}$

x³-0.2x²+3.276·10^-4 =0

cuyas raíces son

x₁=-0.0362, x₂=0.195, x₃=0.0447 m

La primera no es físicamente posible, la segunda corresponde a un mínimo de la energía potencial (posición de equilibrio estable) y la tercera, corresponde a un máximo (posición de equilibrio inestable).

La carga crítica q_c y la separación de equilibrio de las cargas es

${\displaystyle \begin{array}{l}{q}_c=\frac{2x_0}{3}\sqrt{\frac{2\pi x_0{\epsilon }_{0}mg}{3d}}=25.4·{10}^{-9}\text{C}\\ x=\sqrt[3]{\frac{q_c^{2}d}{\pi {\epsilon }_{0}mg}}=13.3\text{cm}\end{array}}$

Si la carga de las partículas q>q_c las dos partículas se juntan, su separación x=0.

En realidad, las partículas tienen un tamaño y no pueden ocupar la misma posición.

Actividades

Se ha fijado

• La masa de las partículas, m=0.001 kg

• La longitud del hilo, d=1.0 m

• La separación entre las partículas no cargadas x₀=0.2 m

Se introduce

• La carga q de las partículas en unidades 10^-9 C, en el control titulado Carga.

Se pulsa el botón titulado Nuevo

En la parte derecha, se representa la energía potencial en E_p en función de la separación x entre las partículas. Se señala el máximo y el mínimo, si existen.

Histéresis en un sistema electromecánico

Se produce el fenómeno de la histéresis, cuando el sistema puede existir en varios estados estables para valores dados de las variables externas (o parámetros de control), y que éstos se pueden alcanzar por una variación lenta de los parámetros.  Un ejemplo típico es la magnetización de un material ferromagnético por un campo magnético externo.

El comportamiento del sistema físico que aquí se estudia está descrito por la separación x entre los centros de las cargas. El parámetro que cambia es la carga q de cada una de las esferas. En ciertos casos, cuando se alcanzan valores críticos de la carga q, el comportamiento del sistema experimenta un salto. Por otra parte, el comportamiento del sistema no es el mismo cuando se incrementa la carga que cuando se disminuye.

En este apartado, se describe una situación más realista que se produce cuando las cargas no son puntuales sino que tienen un tamaño finito. Para evitar los problemas derivados de la polarización de la carga de una esfera metálica en el campo de la otra, o de la descarga de las esferas en el momento en que entran en contacto. Supondremos que  las cargas puntuales están el centro de dos esferas aislantes rígidas de radio r.

La diferencia por tanto, entre las cargas puntales y las esferas de radio r estriba en que la separación mínima entre cargas puntuales es cero, mientras que la separación mínima entre esferas rígidas de radio r es 2r.

• Para cada carga q comprendida entre q=0 y q=q_c, existen dos posiciones de equilibrio, una estable y otra inestable.

• Cuando q=q_c las dos posiciones de equilibrio coinciden en un punto de inflexión.

• Cuando q>q_c no hay posiciones de equilibrio para x>0

En la figura inferior, se muestra:

• En color azul, las posiciones de equilibrio estable x, para las cargas q comprendidas entre 0 y q_c

• En color rojo, las posiciones de equilibrio inestable x, para las cargas q comprendidas entre 0 y q_c

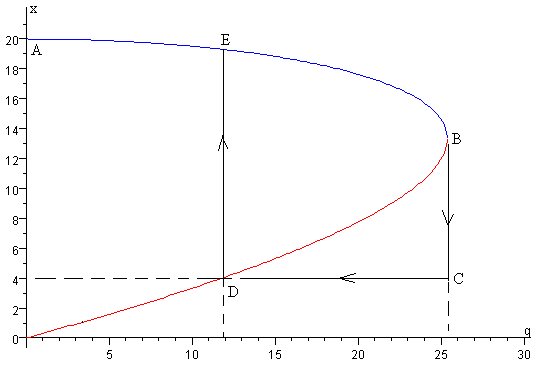
Vamos a incrementar la carga de las esferas desde q=0 y a observar la separación x entre las mismas. El comportamiento del sistema sigue el camino ABCDEA, con dos cambios bruscos BC y DE. Como vemos, el camino de ida AB cuando la carga se incrementa de 0 a q_c no coincide con el de vuelta BCDEA cuando la carga disminuye de q_c a 0. A continuación, se explica las distintas etapas:

Etapa AB

Cuando la carga q se incrementa de 0 a q_c la separación va disminuyendo desde x₀ a x_c dados por las expresiones.

${\displaystyle q_c=\frac{2x_0}{3}\sqrt{\frac{2\pi x_0{\epsilon }_{0}mg}{3d}}{x}_c=\sqrt[3]{\frac{q_c^{2}d}{\pi {\epsilon }_{0}mg}}}$

El comportamiento del sistema viene descrito por la curva de color azul AB de la figura, que corresponde a las posiciones de equilibrio estable.

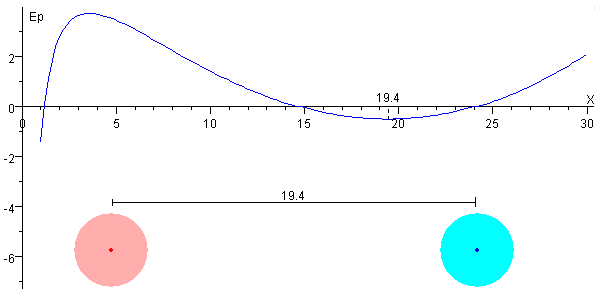
Etapa BC

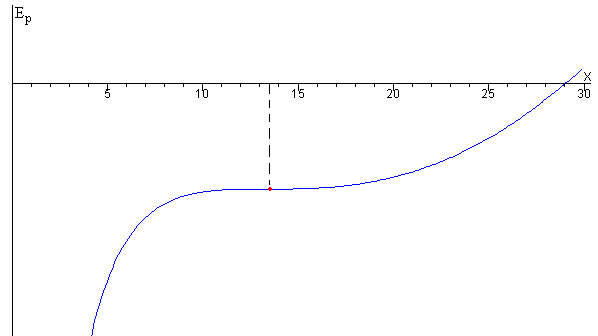
Cuando la carga q supera el valor crítico q_c se produce un cambio brusco BC, la separación entre las cargas puntuales sería cero, pero si son esferas rígidas de radio r la separación será x=2r.

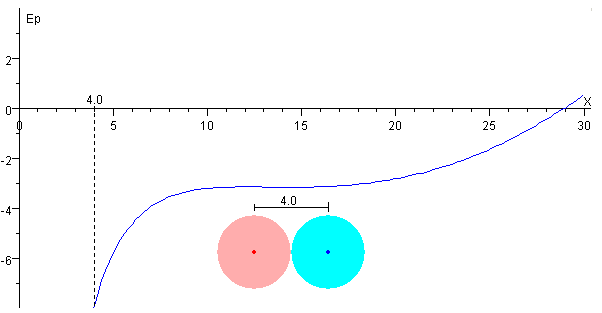
Etapa CD

Si se disminuye la carga q, la separación de las esferas seguirá siendo x=2r ya que la energía potencial de esta configuración es la mínima posible, tal como se muestra en la figura

o es inferior al máximo adyacente, tal como se muestra más abajo. Como vemos, hay un máximo interpuesto que impide que la esfera alcance una posición de menor energía, en el mínimo de la parte derecha de la curva.

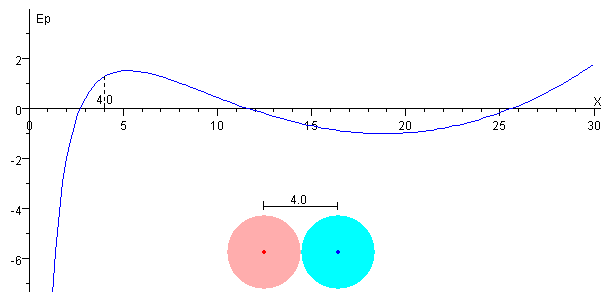
El comportamiento del sistema está descrito por la recta DE

El punto D corresponde a la carga q_l para la cual la energía potencial alcanza un valor máximo cuando la separación entre cargas es x=2r. Ponemos x=2r en la ecuación cúbica que nos proporciona las posiciones de equilibrio y despejamos q

${\displaystyle \begin{array}{l}{x}^3-x_0{x}^2+\frac{d{q}^2}{2\pi {\epsilon }_{0}mg}=0\\ q_l=r\sqrt{\frac{4\pi {\epsilon }_{0}mg}{d}(2x_0-4r)}\end{array}}$

Etapa DE

Si q<q_l se produce otro cambio brusco DE, la separación aumenta al valor correspondiente a la posición de equilibrio estable de q_l.

Como una de las raíces de la ecuación cúbica es 2r buscamos las otras dos raíces a y b

${\displaystyle \begin{array}{l}(x-2r)(x-a)(x-b)=x^3-x_0{x}^2+\frac{d{q}_l^2}{2\pi {\epsilon }_{0}mg}\\ x^3-(a+b+2r)x^2+(ab+2ra+2rb)x-2rab=x^3-x_0{x}^2+2r^2(2x_0-4r)\\ a+b=x_0-2r\\ ab=-2r(x_0-2r)\end{array}}$

Resolvemos el sistema de dos ecuaciones con dos incógnitas a y b

b²-(x₀-2r)b-2r(x₀-2r)=0

La raíz positiva la llamamos x_l

${\displaystyle x_l=\frac{x_0-2r+\sqrt{(x_0-2r)(x_0+6r)}}{2}}$

Etapa EA

Una vez que el sistema alcanza el punto E, retorna al punto de partida A a través de la porción de curva azul EA que corresponde a posiciones de equilibrio estable.

Ejemplo:

• Masa de las partículas m=0.001 kg
• Carga de las partículas q=13·10^-9 C
• Longitud del hilo d=1.0 m
• Separación entre las partículas no cargadas x₀=0.2 m

• Radio de las esferas r=2 cm =0.02 m

El primer cambio brusco ocurre en el punto B, que corresponde a la carga crítica q_c y a la separación crítica x_c calculada en el apartado Aproximaciones

q_c=25.4·10-9 C, x_c=13.3 cm

El segundo cambio brusco ocurre desde el punto D al punto E

El punto D corresponde a una separación 2r=0.04 m, y la carga q_l de las esferas es

${\displaystyle q_l=r\sqrt{\frac{4\pi {\epsilon }_{0}mg}{d}(2x_0-4r)}=11.8·{10}^{-9}\text{C}}$

El punto E corresponde a la posición de equilibrio estable de las esferas cargadas con una carga q_l

${\displaystyle x_l=\frac{x_0-2r+\sqrt{(x_0-2r)(x_0+6r)}}{2}=19.3\text{cm}}$

Actividades

Se ha fijado

• La masa de las partículas, m=0.001 kg

• La longitud del hilo, d=1.0 m

• La separación entre las partículas no cargadas x₀=0.2 m

Se introduce

• El radio r de las esferas en cm, en el control titulado Radio.

• Se activa la casilla titulada Histéresis

Se pulsa el botón titulado Nuevo

Observamos el comportamiento del sistema formado por las dos esferas cargadas, cuando la carga de aumenta y cuando disminuye. Los dos cambios bruscos de comportamiento que ocurren cuando q=q_c en el camino de ida y cuando x=2r en el camino de vuelta.

• La curva de color azul, corresponde a las posiciones x de equilibrio estable para cualquier carga comprendida entre 0 y q_c.

• La curva de color roja, corresponde a las posiciones x de equilibrio inestable para cualquier carga comprendida entre 0 y q_c.

Activamos la casilla titulada Potencial

Observamos el comportamiento del sistema formado por las dos esferas cargadas, en relación a la curva de energía potencial para cada carga q. El sistema adopta la configuración de energía potencial mínima, compatible con que la separación mínima posible es 2r.

• La carga q se da en unidades de 10^-9 C

• La energía potencial E_p(x) en unidades 10^-6 J

Referencias

Physics Challenge for Teachers and Students. Downton Abbey. The Physics Teacher, Vol. 57, March 2019, pp. 200
Solución, Phys. Teach. 57, A419 (2019)

Partensky P. D., Partensky M. B..Hanging by a thread. The Physics Teacher, 44 February 2006, pp. 88-91