Anillo

Potencial producido por el anillo cargado en el punto fuera del eje

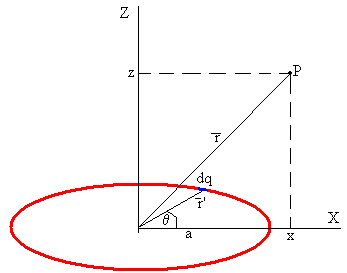
Calculamos el potencial en el punto P del plano XZ producido por un elemento diferencial de carga dq=λ·dl, donde λ=q/(2πa) es la densidad lineal de carga en C/m, dl=a·dθ es la longitud de un arco diferencial,

El vector $\overrightarrow{r}\text{'}=a\cos \theta ·\widehat{i}+a\sin \theta ·\widehat{j}$ señala la posición del elemento diferencial de carga

El vector $\overrightarrow{r}=x\widehat{i}+z\widehat{k}$ señala la posición del punto P

El potencial en el punto P vale

${\displaystyle V=\frac{1}{4\pi {\epsilon }_0}{{\displaystyle \oint }}^{\text{}}\frac{\lambda ·dl}{|\overrightarrow{r}-\overrightarrow{r}\text{'}|}}$

el denominador es la distancia entre el elemento diferencial de carga dq y el punto P.

${\displaystyle |\overrightarrow{r}-\overrightarrow{r}\text{'}|=\sqrt{{(x-a\cos \theta )}^2+a^2{\sin }^2\theta +z^2}=\sqrt{x^2+a^2+z^2-2ax\cos \theta }}$

La integral se convierte en

${\displaystyle \begin{array}{l}{\displaystyle \oint \frac{\lambda ·a·d\theta }{\sqrt{x^2+z^2+a^2-2ax\cos \theta }}}=\frac{2}{4\pi {\epsilon }_0}{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{\lambda ·a·d\theta }{\sqrt{x^2+z^2+a^2-2ax\cos \theta }}}=\\ \frac{\lambda a}{2\pi {\epsilon }_0\sqrt{2ax}}{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{d\theta }{\sqrt{b-\cos \theta }}}b=\frac{z^2+x^2+a^2}{2ax}\end{array}}$

Las tablas de integrales elípticas (Good) nos da la siguiente equivalencia

${\displaystyle {\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{d\theta }{\sqrt{b-\cos \theta }}}=\sqrt{2m}K(m)K(m)={\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{d\phi }{\sqrt{1-m{\sin }^2\phi }}}m=\frac{2}{1+b}}$

K(m) es la integral elíptica completa de primera especie

El potencial V(x,z) vale

${\displaystyle \begin{array}{l}V=\frac{\lambda }{2\pi {\epsilon }_0}\sqrt{\frac{a}{x}m}·K(m)\\ V(x,z)=\frac{q}{2{\pi }^2{\epsilon }_0}\frac{K(m)}{\sqrt{z^2+{(x+a)}^2}}m=\frac{4ax}{z^2+{(x+a)}^2}\end{array}}$

Para puntos del eje del anillo, x=0, m, K(0)=π/2, el potencial vale

${\displaystyle V(z)=\frac{q}{4\pi {\epsilon }_0}\sqrt{\frac{1}{z^2+a^2}}}$

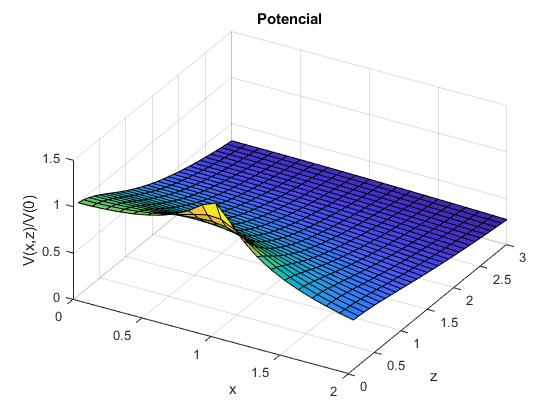
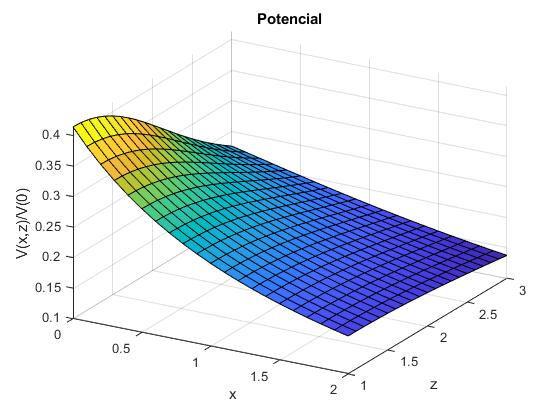
Representamos el potencial V(x,z)/V(0) de los puntos del plano XZ

a=1; %radio
[x,z]=meshgrid(0:0.1:2,0.1:0.1:3);
m=4*a*x./(z.^2+(x+a).^2);
V=2*a*ellipke(m)./sqrt(z.^2+(x+a).^2)/pi;
surf(x,z,V)
xlabel('x')
ylabel('z')
zlabel('V(x,z)')
title('Potencial')
view(30,47)

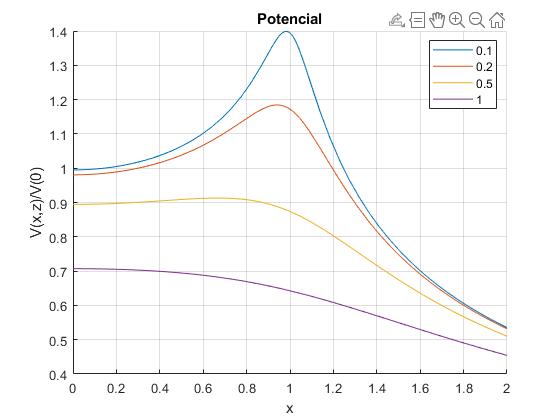
Representamos V(x,z)/V(0), para varios valores de z

a=1; %radio
hold on
for z=[0.1,0.2,0.5,1]
    m=@(x) 4*a*x./(z.^2+(x+a).^2);
    V=@(x) 2*a*ellipke(m(x))./sqrt(z.^2+(x+a).^2)/pi;
    fplot(V,[0,2], 'displayName',num2str(z))
end
hold off
grid on
xlabel('x')
legend('-DynamicLegend','location','best')
ylabel('V(x,z)')
title('Potencial')

Campo eléctrico producido por el anillo cargado en el punto fuera del eje

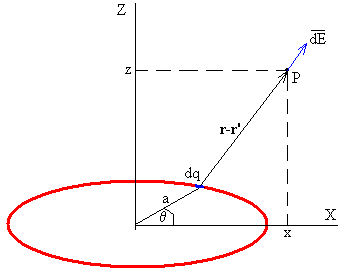
Calculamos el campo eléctrico en el punto P del plano XZ producido por un elemento diferencial de carga dq=λ·dl, donde λ=q/(2πa) es la densidad lineal de carga en C/m, dl=a·dθ es la longitud de un arco diferencial,

El vector $\overrightarrow{r}\text{'}=a\cos \theta ·\widehat{i}+a\sin \theta ·\widehat{j}$ señala la posición del elemento diferencial de carga

El vector $\overrightarrow{r}=x\widehat{i}+z\widehat{k}$ señala la posición del punto P

El campo eléctrico producido por el elemento diferencial de carga $\overrightarrow{dE}$ tiene la dirección y el sentido del vector diferencia $\overrightarrow{r}-\overrightarrow{r}\text{'}$, que une la posición de la carga y el punto P.

${\displaystyle \overrightarrow{dE}=\frac{1}{4\pi {\epsilon }_0}\frac{\lambda ·dl}{|\overrightarrow{r}-\overrightarrow{r}\text{'}{|}^2}\frac{\overrightarrow{r}-\overrightarrow{r}\text{'}}{|\overrightarrow{r}-\overrightarrow{r}\text{'}|}=\frac{1}{4\pi {\epsilon }_0}\frac{\lambda ·dl}{|\overrightarrow{r}-\overrightarrow{r}\text{'}{|}^3}\left(\overrightarrow{r}-\overrightarrow{r}\text{'}\right)}$

Las componentes del campo total son:

${\displaystyle \begin{array}{l}{E}_x=\frac{\lambda a}{4\pi {\epsilon }_0}{\displaystyle \oint \frac{x-a\cos \theta }{{(x^2+z^2+a^2-2ax\cos \theta )}^{3/2}}}d\theta \\ E_y=\frac{\lambda a}{4\pi {\epsilon }_0}{\displaystyle \oint \frac{-a\sin \theta }{{(x^2+z^2+a^2-2ax\cos \theta )}^{3/2}}}d\theta \\ E_z=\frac{\lambda a}{4\pi {\epsilon }_0}{\displaystyle \oint \frac{z}{{(x^2+z^2+a^2-2ax\cos \theta )}^{3/2}}}d\theta \end{array}}$

Por simetría, la componente Y del campo debe anularse, como puede comprobarse fácilmente resolviendo la integral inmediata.

Como cosθ es una función par, hacemos la sustitución ${\displaystyle \underset{0}{\overset{2\pi }{\int }}}\to 2{\displaystyle \underset{0}{\overset{\pi }{\int }}}$

El resultado es

${\displaystyle \begin{array}{l}{E}_x=\frac{2\lambda a}{4\pi {\epsilon }_0}{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{x-a\cos \theta }{{\left(x^2+z^2+a^2-2ax\cos \theta \right)}^{3/2}}d\theta }=\\ \frac{\lambda a}{2\pi {\epsilon }_0}\frac{1}{{\left(2ax\right)}^{3/2}}\left(x{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{d\theta }{{\left(b-\cos \theta \right)}^{3/2}}}-a{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{\cos \theta ·d\theta }{{\left(b-\cos \theta \right)}^{3/2}}}\right)\\ E_z=\frac{2\lambda a}{4\pi {\epsilon }_0}{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{z}{{\left(x^2+z^2+a^2-2ax\cos \theta \right)}^{3/2}}}d\theta =\\ \frac{\lambda a}{2\pi {\epsilon }_0}\frac{1}{{\left(2ax\right)}^{3/2}}z{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{d\theta }{{\left(b-\cos \theta \right)}^{3/2}}}\end{array}}$

Las tablas de integrales elípticas (Good) nos da las siguientes equivalencias

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{d\theta }{{\left(b-\cos \theta \right)}^{3/2}}}=\frac{m}{2-2m}\sqrt{2m}E\left(m\right)\\ E\left(m\right)={\displaystyle \underset{0}{\overset{\pi /2}{\int }}\sqrt{1-m{\sin }^2\phi }d\phi }m=\frac{2}{1+b}\\ {\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{-\cos \theta ·d\theta }{{\left(b-\cos \theta \right)}^{3/2}}}=\sqrt{2m}K\left(m\right)-\frac{2-m}{2-2m}\sqrt{2m}E\left(m\right)\\ K\left(m\right)={\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{d\phi }{\sqrt{1-m{\sin }^2\phi }}}\end{array}}$

Las expresiones de las componentes del campo son

${\displaystyle \begin{array}{l}{E}_x=\frac{q}{4{\pi }^2{\epsilon }_0}\frac{1}{{\left(2ax\right)}^{3/2}}\left(x\frac{m}{2-2m}\sqrt{2m}E(m) +a\sqrt{2m}K(m)-a\frac{2-m}{2-2m}\sqrt{2m}E(m)\right)\hfill \\ E_z=\frac{q}{4{\pi }^2{\epsilon }_0}\frac{1}{{\left(2ax\right)}^{3/2}}z\frac{m}{2-2m}\sqrt{2m}E(m)m=\frac{4ax}{z^2+{\left(x+a\right)}^2}\hfill \end{array}}$

Simplificando, obtenemos las siguientes expresiones

${\displaystyle \begin{array}{l}{E}_x=\frac{q}{4{\pi }^2{\epsilon }_0}\left\{\frac{4x}{{\left(z^2+{\left(x+a\right)}^2\right)}^{3/2}}\frac{E(m)}{2-2m}+\frac{1}{x\sqrt{z^2+{\left(x+a\right)}^2}}\left(K(m)-\frac{2-m}{2-2m}E(m)\right)\right\}\\ E_z=\frac{q}{4{\pi }^2{\epsilon }_0}\frac{4z}{{\left(z^2+{\left(x+a\right)}^2\right)}^{3/2}}\frac{E(m)}{2-2m}m=\frac{4ax}{z^2+{\left(x+a\right)}^2}\end{array}}$

Representamos el vector campo eléctrico en puntos del plano XZ

a=1; %radio
[x,z]=meshgrid(0:0.1:2,0.1:0.1:1.5);
m=4*a*x./(z.^2+(x+a).^2);
[K,E]=ellipke(m);
Ex=4*x.*E./((z.^2+(x+a).^2).^(3/2).*(2-2*m))+(K-(2-m).*E./(2-2*m)).
/(x.*sqrt(z.^2+(x+a).^2));
Ez=4*z.*E./((z.^2+(x+a).^2).^(3/2).*(2-2*m));
quiver(x,z,Ex,Ez, 2, 'color','r')
xlabel('x')
ylabel('z')
title('Campo eléctrico')   

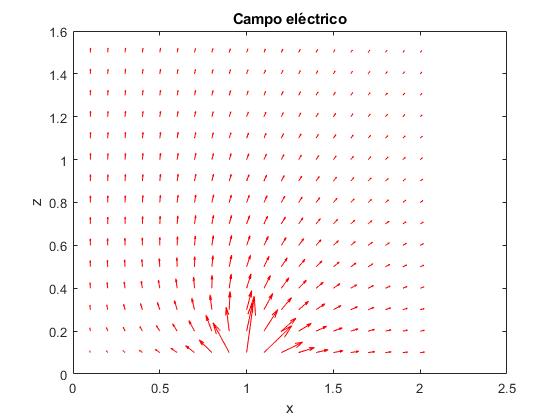
En la figura, se muestra la dirección del campo eléctrico mediante flechas, en el plano XZ, con x>0  y z>0. El módulo del campo cambia significativamente de un punto cercano al anillo a otro algo más alejado. En esta otra representación se puede apreciar mejor la dirección del campo eléctrico

Caso particular

Estudiamos el campo a lo largo del eje del anillo, x →0,

${\displaystyle m\to \frac{4ax}{z^2+a^2}}$

Las integrales elípticas tienden ambas a K(0)=E(0)=π/2. Para la componente E_x, los dos últimos términos entre paréntesis se cancelan.

${\displaystyle \begin{array}{l}{E}_x=\frac{q}{4{\pi }^2{\epsilon }_0}\frac{x}{{\left(z^2+{\left(x+a\right)}^2\right)}^{3/2}}\\ E_z=\frac{q}{4{\pi }^2{\epsilon }_0}\frac{z}{{\left(z^2+{\left(x+a\right)}^2\right)}^{3/2}}\end{array}}$

Disco cargado

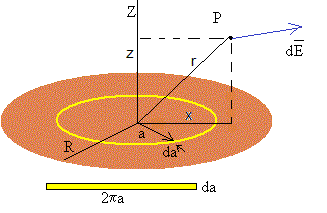
Para un disco de radio R, dividimos el disco en anillos de radio a y espesor da. Cada anillo tiene una carga dq=σ(2πa·da). El potencial producido por este anillo en P es

${\displaystyle dV=\frac{\sigma 2\pi a·da}{2{\pi }^2{\epsilon }_0}\frac{K(m)}{\sqrt{z^2+{(x+a)}^2}}m=\frac{4ax}{z^2+{(x+a)}^2}}$

El potencial V(x,z) producido por el disco cargado es

${\displaystyle V(x,z)=\frac{\sigma }{\pi {\epsilon }_0}{\displaystyle \underset{0}{\overset{R}{\int }}\frac{K(m)}{\sqrt{z^2+{(x+a)}^2}}a·da}}$

Representamos el potencial V(x,z) en unidades del potencial en el centro del disco V(0)=σR/(2ε₀)

function disco_cargado_9()
    R=1; %radio del disco
    xx=0:0.1:2;
    zz=1:0.1:3;
    V=zeros(length(xx),length(zz));
    i=0; j=0;
    for x=xx
        i=i+1;
        j=0;
        for z=zz
            j=j+1;
            V(i,j)=integral(@potencial,0,R)*2/(pi*R);
        end
    end
    [x,z]=meshgrid(xx,zz);
    surf(x,z,V)
    xlabel('x')
    ylabel('z')
    zlabel('V(x,z)/V(0)')
    title('Potencial')
    view(30,30)

    function res=potencial(a)
        m=4*a.*x./(z^2+(x+a).^2);
        res=a.*ellipke(m)./sqrt(z^2+(x+a).^2);
    end
end

Representamos V(x,z), en unidades del potencial en el centro del disco V(0)=σR/(2ε₀), para varios valores de z

function disco_cargado_10()
    R=1; %radio del disco
    hold on
    X=linspace(0,2,100);
    V=zeros(1,length(X));
    for z=[0.1,0.2,0.5,1]
        i=1;
        for x=X
            V(i)=integral(@ potencial, 0,R)*2/(pi*R);
            i=i+1;
        end
        plot(X,V, 'displayName',num2str(z))
    end
    hold off
    grid on
    xlabel('x')
    legend('-DynamicLegend','location','best')
    ylabel('V(x,z)/V(0)')
    title('Potencial')

    function res=potencial(a)
        m=4*a.*x./(z^2+(x+a).^2);
        res=a.*ellipke(m)./sqrt(z^2+(x+a).^2);
    end
end

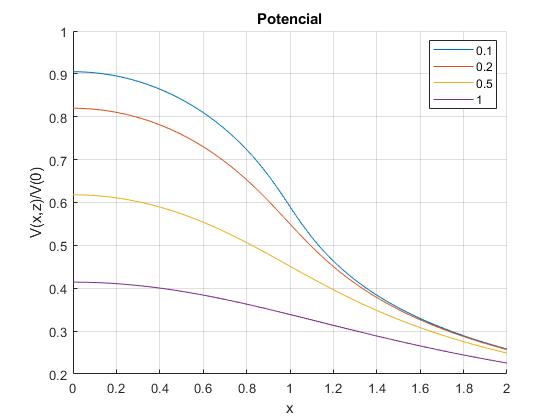
Campo eléctrico producido por el disco cargado en el punto fuera del eje

Dividimos el disco en anillos de radio a y espesor da. Cada anillo tiene una carga dq=σ(2πa·da). Las componentes del campo eléctrico producido por este anillo en P es

${\displaystyle \begin{array}{l}d{E}_x=\frac{\sigma 2\pi a·da}{4{\pi }^2{\epsilon }_0}\left\{\frac{4x}{{\left(z^2+{\left(x+a\right)}^2\right)}^{3/2}}\frac{E(m)}{2-2m}+\frac{1}{x\sqrt{z^2+{\left(x+a\right)}^2}}\left(K(m)-\frac{2-m}{2-2m}E(m)\right)\right\}\\ d{E}_z=\frac{\sigma 2\pi a·da}{4{\pi }^2{\epsilon }_0}\frac{4z}{{\left(z^2+{\left(x+a\right)}^2\right)}^{3/2}}\frac{E(m)}{2-2m}m=\frac{4ax}{z^2+{\left(x+a\right)}^2}\end{array}}$

El campo eléctrco producido por el disco cargado es

${\displaystyle \begin{array}{l}{E}_x=\frac{\sigma }{2\pi {\epsilon }_0}{\displaystyle \underset{0}{\overset{R}{\int }}\left\{\frac{4x}{{\left(z^2+{\left(x+a\right)}^2\right)}^{3/2}}\frac{E(m)}{2-2m}+\frac{1}{x\sqrt{z^2+{\left(x+a\right)}^2}}\left(K(m)-\frac{2-m}{2-2m}E(m)\right)\right\}a·da}\\ E_z=\frac{\sigma }{2\pi {\epsilon }_0}{\displaystyle \underset{0}{\overset{R}{\int }}\left\{\frac{4z}{{\left(z^2+{\left(x+a\right)}^2\right)}^{3/2}}\frac{E(m)}{2-2m}\right\}a·da}\end{array}}$

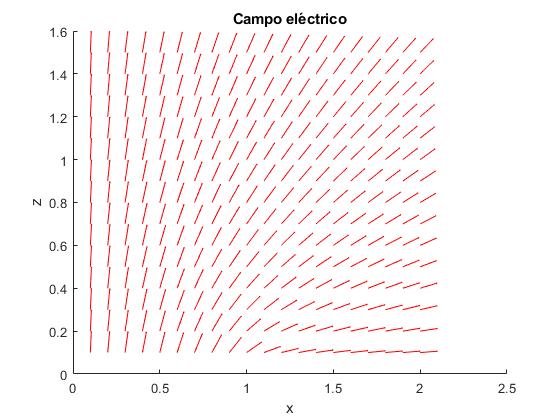
En la figura, se muestra la dirección del campo eléctrico mediante flechas, en el plano XZ, con x>0  y z>0. El módulo del campo no se puede mostrar ya que cambia significativamente de un punto cercano al disco a otro algo más alejado.

function disco_cargado_3()
    R=1; %radio del disco
    hold on
    for x=0.1:0.1:2
        for z=0.1:0.1:1.5
            Ex=integral(@campo_x,0,R)/pi;
            Ez=integral(@campo_z,0,R)/pi;
            modulo=sqrt(Ex^2+Ez^2);
            quiver(x,z,Ex/modulo,Ez/modulo, 0.1, 'color','r')
        end
    end
    hold off
    xlabel('x')
    ylabel('z')
    title('Campo eléctrico')   
    function res=campo_x(a)
        m=4*a*x./(z^2+(x+a).^2);
        [K,E]=ellipke(m);
        res=a.*(4*x*E./((z^2+(x+a).^2).^(3/2).*(2-2*m))+(K-(2-m).*E./(2-2*m)).
/(x*sqrt(z^2+(x+a).^2)));
    end
    function res=campo_z(a)
        m=4*a*x./(z^2+(x+a).^2);
        [~,E]=ellipke(m);
        res=a.*(4*z*E./((z^2+(x+a).^2).^(3/2).*(2-2*m))); 
    end
end

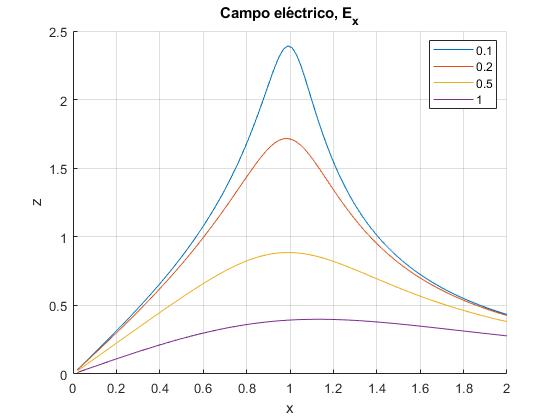
Representamos la componente E_x del campo eléctrico para varios valores de z

function disco_cargado_11()
    R=1; %radio del disco
    hold on
    X=linspace(0,2,100);
    Ex=zeros(1,length(X));
    for z=[0.1,0.2,0.5,1]
        i=1;
        for x=X
            Ex(i)=integral(@campo_x,0,R);
            i=i+1;
        end
        plot(X,Ex, 'displayName',num2str(z))
    end
    hold off
    grid on
    legend('-DynamicLegend','location','best')
    xlabel('x')
    ylabel('z')
    title('Campo eléctrico, E_x')   
    
    function res=campo_x(a)
        m=4*a*x./(z^2+(x+a).^2);
        [K,E]=ellipke(m);
        res=a.*(4*x*E./((z^2+(x+a).^2).^(3/2).*(2-2*m))+(K-(2-m).*E./(2-2*m)).
/(x*sqrt(z^2+(x+a).^2)));
    end
end

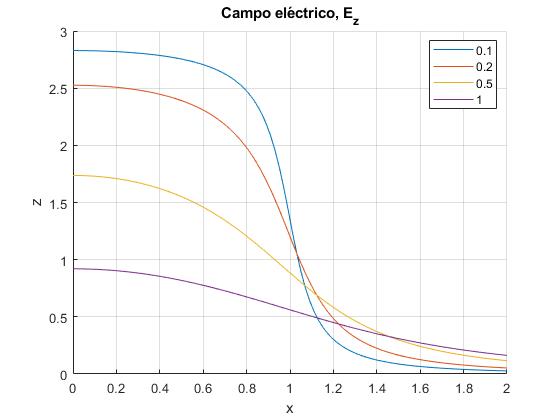
Representamos la componente E_z del campo eléctrico para varios valores de z

function disco_cargado_12()
    R=1;
    hold on
    X=linspace(0,2,100);
    Ez=zeros(1,length(X));
    for z=[0.1,0.2,0.5,1]
        i=1;
        for x=X
            Ez(i)=integral(@campo_z,0,R);
            i=i+1;
        end
        plot(X,Ez, 'displayName',num2str(z))
    end
    hold off
    grid on
    legend('-DynamicLegend','location','best')
    xlabel('x')
    ylabel('z')
    title('Campo eléctrico, E_z')   
    
    function res=campo_z(a)
        m=4*a*x./(z^2+(x+a).^2);
        [~,E]=ellipke(m);
        res=a.*(4*z*E./((z^2+(x+a).^2).^(3/2).*(2-2*m))); 
    end
end

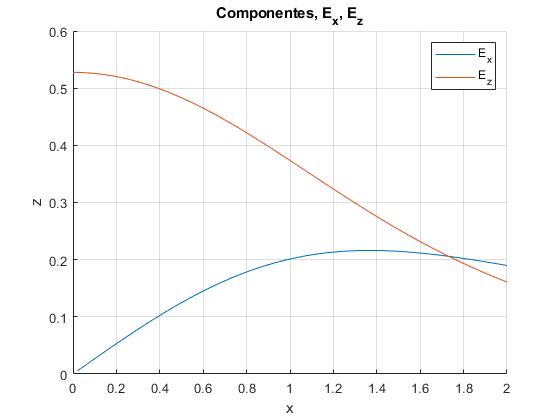
Representamos en la misma gráfica las componentes E_x y E_z para z=1.5

function disco_cargado_12()
    R=1;
    hold on
    X=linspace(0,2,100);
    Ez=zeros(1,length(X));
    Ex=zeros(1,length(X));
    z=1.5;
    i=1;
    for x=X
        Ez(i)=integral(@campo_z,0,R);
        Ex(i)=integral(@campo_x,0,R);
        i=i+1;
    end
    plot(X,Ex)
    plot(X,Ez)
    hold off
    grid on
    legend('E_x','E_z')
    xlabel('x')
    ylabel('z')
    title('Componentes, E_x, E_z')   

    function res=campo_x(a)
        m=4*a*x./(z^2+(x+a).^2);
        [K,E]=ellipke(m);
        res=a.*(4*x*E./((z^2+(x+a).^2).^(3/2).*(2-2*m))+(K-(2-m).*E./(2-2*m)).
/(x*sqrt(z^2+(x+a).^2)));
    end
    function res=campo_z(a)
        m=4*a*x./(z^2+(x+a).^2);
        [~,E]=ellipke(m);
        res=a.*(4*z*E./((z^2+(x+a).^2).^(3/2).*(2-2*m))); 
    end
end

Referencias

Zypman F. R., Electric field of a ring of charge. Am. J. Phys. 74 (4) April 2006, pp. 295-300.

Good R. H. Elliptic integrals, the forgotten functions. Eur. J. Phys. 22 (2001) pp. 119-126.