Energía de una distribución de cargas

Vamos a calcular ahora la energía necesaria para formar la distribución uniforme de carga positiva. O bien, la energía que se liberaría cuando la distribución uniforme de carga positiva explotase de modo que cada parte de ella estuviese a una distancia infinita una de la otra.

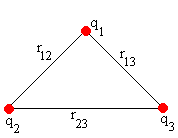
Determinaremos la expresión de la energía de un sistema de tres cargas y la generalizamos para una distribución continua de carga.

Consideremos un sistema de tres cargas puntuales fijas q₁, q₂ y q₃, tal como se indica en la figura.

La energía de este sistema U vale

${\displaystyle U=E_{p12}+E_{p13}+E_{p23}=\frac{1}{4\pi {\epsilon }_0}\frac{q_1{q}_2}{r_{12}}+\frac{1}{4\pi {\epsilon }_0}\frac{q_1{q}_3}{r_{13}}+\frac{1}{4\pi {\epsilon }_0}\frac{q_2{q}_3}{r_{23}}}$

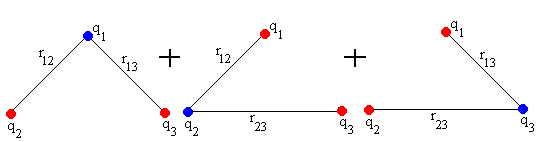
Llamando V₁ al potencial producido por las cargas q₂ y q₃ en la posición que ocupa q₁. La energía de la carga q₁ en el campo producido por las otras dos es

${\displaystyle q_1{V}_1=q_1\left(\frac{1}{4\pi {\epsilon }_0}\frac{q_3}{r_{13}}+\frac{1}{4\pi {\epsilon }_0}\frac{q_2}{r_{12}}\right)=\frac{1}{4\pi {\epsilon }_0}\frac{q_1{q}_3}{r_{13}}+\frac{1}{4\pi {\epsilon }_0}\frac{q_1{q}_2}{r_{12}}}$

Análogamente, llamando V₂ al potencial producido por las cargas q₁ y q₃ en la posición que ocupa q₂. La energía de la carga q₂ en el campo producido por las otras dos es

${\displaystyle q_2{V}_2=q_2\left(\frac{1}{4\pi {\epsilon }_0}\frac{q_1}{r_{12}}+\frac{1}{4\pi {\epsilon }_0}\frac{q_3}{r_{23}}\right)=\frac{1}{4\pi {\epsilon }_0}\frac{q_1{q}_2}{r_{12}}+\frac{1}{4\pi {\epsilon }_0}\frac{q_2{q}_3}{r_{23}}}$

Del mismo modo, llamando V₃ al potencial producido por las cargas q₁ y q₂ en la posición que ocupa q₃. La energía de la carga q₃ en el campo producido por las otras dos es

${\displaystyle q_3{V}_3=q_3\left(\frac{1}{4\pi {\epsilon }_0}\frac{q_1}{r_{13}}+\frac{1}{4\pi {\epsilon }_0}\frac{q_2}{r_{23}}\right)=\frac{1}{4\pi {\epsilon }_0}\frac{q_1{q}_3}{r_{13}}+\frac{1}{4\pi {\epsilon }_0}\frac{q_2{q}_3}{r_{23}}}$

Sumando estas tres contribuciones obtenemos el doble de la energía del sistema de partículas

${\displaystyle U=\frac{1}{2}\left(q_1{V}_1+q_2{V}_2+q_3{V}_3\right)=\frac{1}{2}{\displaystyle \sum q_i{V}_i}}$

Energía de una esfera cargada

Volviendo de nuevo a la esfera uniformemente cargada, el potencial V_i se sustituye por el potencial en la posición r, V(r) que hemos calculado en la página titulada Ley de Gauss.

La carga q_i se sustituye por la carga que hay en la capa esférica comprendida entre r y r+dr. El volumen de dicha capa esférica es 4πr²dr, y la carga que hay en este volumen vale (densidad de carga por volumen)

${\displaystyle dq=\frac{3Q{r}^2}{R^3}dr}$

La energía vale entonces

${\displaystyle U=\frac{1}{2}{\displaystyle \underset{0}{\overset{R}{\int }}V(r)dq}=\frac{1}{2}{\displaystyle \underset{0}{\overset{R}{\int }}\frac{Q}{4\pi {\epsilon }_{0}R}\left(\frac{3}{2}-\frac{1}{2}\frac{r^2}{R^2}\right)\frac{3Q{r}^2}{R^3}dr}=\frac{3}{5}\frac{Q^2}{4\pi {\epsilon }_{0}R}}$

Cálculo alternativo

${\displaystyle U={\displaystyle \underset{\text{todo el espacio}}{\int }\left(\frac{1}{2}{\epsilon }_0{E}^2\right)}dV}$

Para una esfera unifomemente cargada

${\displaystyle E=\{\begin{array}{l}\frac{Qr}{4\pi {\epsilon }_0{R}^3},r\le R\\ \frac{Q}{4\pi {\epsilon }_0{r}^2},r>R\end{array}}$

El volumen de la capa esférica comprendida entre r y r+dr es dV=4πr²dr

${\displaystyle U=\frac{1}{2}{\epsilon }_0{{\displaystyle \underset{0}{\overset{R}{\int }}\left(\frac{Qr}{4\pi {\epsilon }_0{R}^3}\right)}}^{2}4\pi r^{2}dr+\frac{1}{2}{\epsilon }_0{{\displaystyle \underset{R}{\overset{\infty }{\int }}\left(\frac{Q}{4\pi {\epsilon }_0{r}^2}\right)}}^{2}4\pi r^{2}dr=\frac{3Q^2}{20\pi {\epsilon }_{0}R}}$

Para una esfera conductora

${\displaystyle E=\{\begin{array}{l}\mathrm{0,}r<R\\ \frac{Q}{4\pi {\epsilon }_0{r}^2},r\ge R\end{array}}$

La energía U es

${\displaystyle U=\frac{1}{2}{\epsilon }_0{{\displaystyle \underset{R}{\overset{\infty }{\int }}\left(\frac{Q}{4\pi {\epsilon }_0{r}^2}\right)}}^{2}4\pi r^{2}dr=\frac{Q^2}{8\pi {\epsilon }_{0}R}}$

Posiciones de equilibrio de un sistema de tres partículas cargadas

Tres partículas de cargas q₁, q₂ y q₃ se mueven sin rozamiento a lo largo de un camino circular de radio a. Las posiciones angulares θ₁, θ₂ y θ₃, de equilibrio son aquellas que hacen mínimo la energía U

${\displaystyle U=\frac{1}{4\pi {\epsilon }_0}\frac{q_1{q}_2}{|\overrightarrow{r_2}-\overrightarrow{r_1}|}+\frac{1}{4\pi {\epsilon }_0}\frac{q_1{q}_3}{|\overrightarrow{r_3}-\overrightarrow{r_1}|}+\frac{1}{4\pi {\epsilon }_0}\frac{q_2{q}_3}{|\overrightarrow{r_3}-\overrightarrow{r_2}|}}$

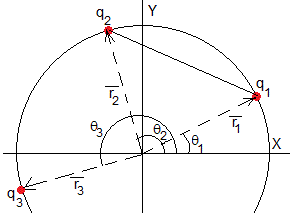
La distancia entre las partículas de carga q₁ y q₂ es

${\displaystyle {\left|\overrightarrow{r_2}-\overrightarrow{r_1}\right|}^2=r_2^2+r_1^2-2\overrightarrow{r_2}\overrightarrow{r_1}=a^2+a^2-2a^2\cos \left({\theta }_2-{\theta }_1\right)=4a^2{\sin }^2\left(\frac{{\theta }_2-{\theta }_1}{2}\right)}$

de modo similar las otras dos distancias. El resultado es

${\displaystyle U=\frac{1}{4\pi {\epsilon }_0}\frac{q_1{q}_2}{2a\sin \left(\frac{{\theta }_2-{\theta }_1}{2}\right)}+\frac{1}{4\pi {\epsilon }_0}\frac{q_1{q}_3}{2a\sin \left(\frac{{\theta }_3-{\theta }_1}{2}\right)}+\frac{1}{4\pi {\epsilon }_0}\frac{q_2{q}_3}{2a\sin \left(\frac{{\theta }_3-{\theta }_2}{2}\right)}}$

Llamando, α=θ₂-θ₁, β=θ₃-θ₂, luego θ₃-θ₁=α+β

${\displaystyle U=\frac{1}{4\pi {\epsilon }_0}\frac{q_1{q}_2}{2a\sin \left(\frac{\alpha }{2}\right)}+\frac{1}{4\pi {\epsilon }_0}\frac{q_1{q}_3}{2a\sin \left(\frac{\alpha +\beta }{2}\right)}+\frac{1}{4\pi {\epsilon }_0}\frac{q_2{q}_3}{2a\sin \left(\frac{\beta }{2}\right)}}$

En el equilibrio la energía U deberá ser mínima

${\displaystyle \begin{array}{l}\frac{\partial U}{\partial \alpha }=\mathrm{0,}-q_1{q}_2\frac{-\frac{1}{2}\cos \left(\frac{\alpha }{2}\right)}{{\sin }^2\left(\frac{\alpha }{2}\right)}-q_1{q}_3\frac{-\frac{1}{2}\cos \left(\frac{\alpha +\beta }{2}\right)}{{\sin }^2\left(\frac{\alpha +\beta }{2}\right)}=0\\ \frac{\partial U}{\partial \beta }=\mathrm{0,}-q_1{q}_3\frac{-\frac{1}{2}\cos \left(\frac{\alpha +\beta }{2}\right)}{{\sin }^2\left(\frac{\alpha +\beta }{2}\right)}-q_2{q}_3\frac{-\frac{1}{2}\cos \left(\frac{\beta }{2}\right)}{{\sin }^2\left(\frac{\beta }{2}\right)}=0\end{array}}$

Resolvemos el sistema no lineal de dos ecuaciones con dos incógnitas

${\displaystyle \begin{array}{l}\frac{\cos \left(\frac{\alpha }{2}\right)}{1-\cos \alpha }+\frac{q_3}{q_2}\frac{\cos \left(\frac{\alpha +\beta }{2}\right)}{1-\cos \left(\alpha +\beta \right)}=0\\ \frac{\cos \left(\frac{\beta }{2}\right)}{1-\cos \beta }+\frac{q_1}{q_2}\frac{\cos \left(\frac{\alpha +\beta }{2}\right)}{1-\cos \left(\alpha +\beta \right)}=0\end{array}}$

Sea un sistema tal que q₁=1, q₂=2 y q₃=3. Utilizamos la función fsolve de MATLAB para resolver el sistema de dos ecuaciones. En el código x(1) es α y x(2) es β

q1=1; %cargas
q2=2;
q3=3;
F=@(x) [cos(x(1)/2)/(1-cos(x(1)))+(q3/q2)*cos((x(1)+x(2))/2)/(1-cos((x(1)+
x(2))/2)); cos(x(2)/2)/(1-cos(x(2)))+(q1/q2)*cos((x(1)+x(2))/2)/
(1-cos((x(1)+x(2))/2))];
sol=fsolve(F,[2*pi/3, 2*pi/3]);
disp(sol) 

    1.7757    2.5008

El resultado es α=1.7757 y β=2.5008. Asignando θ₁=0, los valores de θ₂=α=1.7757 (101.7°) y θ₃=α+β=4.2765 (245.0°). Estas son las posiciones angulares de equilibrio de cada una de las tres cargas

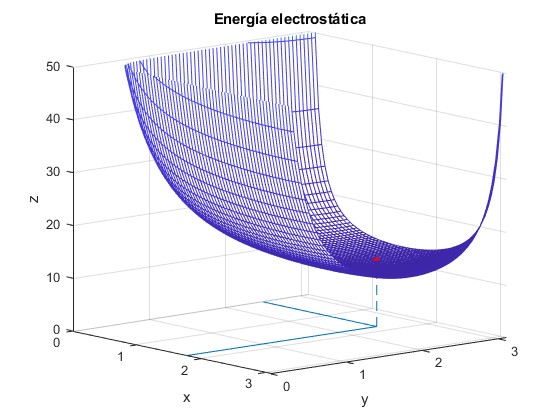
Representamos la energía potencial U(α, β) señalando el mínimo mediante un punto de color rojo

q1=1; %cargas
q2=2;
q3=3;
f=@(x,y) q1*q2./sin(x/2)+q2*q3./sin(y/2)+q1*q3./sin((x+y)/2);
x=0:0.05:pi;
y=0:0.05:pi;
[X,Y]=meshgrid(x,y);
hold on
mesh(X,Y,f(X,Y));
x_m=1.7757;  %mínimo de la energía U       
y_m=2.5008;
z_m=f(x_m,y_m);
plot3(x_m, y_m, z_m,'ro','markersize',4,'markeredgecolor','r',
'markerfacecolor','r')
line([x_m,x_m], [y_m,y_m], [0,z_m],'lineStyle','--' )
line([0,x_m], [y_m,y_m], [0,0] )
line([x_m,x_m], [0,y_m], [0,0])
hold off
grid on
xlabel('x')
ylabel('y')
zlabel('z')
zlim([0,50])
title('Energía electrostática')
view(50,12)

Ecuación del movimiento

Supongamos que las partículas se ponen en movimiento deslizando sin rozamiento a lo largo del camino circular de radio a. Calculamos la energía cinética del sistema de tres partículas

${\displaystyle E_k=\frac{1}{2}{m}_1{\left(a\frac{d{\theta }_1}{dt}\right)}^2+\frac{1}{2}{m}_2{\left(a\frac{d{\theta }_2}{dt}\right)}^2+\frac{1}{2}{m}_3{\left(a\frac{d{\theta }_3}{dt}\right)}^2}$

La lagrangiana L=E_k-U es

${\displaystyle L=\frac{1}{2}{m}_1{\left(a\frac{d{\theta }_1}{dt}\right)}^2+\frac{1}{2}{m}_2{\left(a\frac{d{\theta }_2}{dt}\right)}^2+\frac{1}{2}{m}_3{\left(a\frac{d{\theta }_3}{dt}\right)}^2-\frac{1}{4\pi {\epsilon }_0}\frac{1}{2a}\left\{\frac{q_1{q}_2}{\sin \left(\frac{{\theta }_2-{\theta }_1}{2}\right)}+\frac{q_1{q}_3}{\sin \left(\frac{{\theta }_3-{\theta }_1}{2}\right)}+\frac{q_2{q}_3}{\sin \left(\frac{{\theta }_3-{\theta }_2}{2}\right)}\right\}}$

Las ecuaciones del movimiento son

${\displaystyle \frac{d}{dt}\left(\frac{\partial L}{\partial {\dot{\theta }}_i}\right)-\frac{\partial L}{\partial {\theta }_i}=\mathrm{0,}i=\mathrm{1,2,3}}$

Un sistema de tres ecuaciones diferenciales

${\displaystyle \begin{array}{l}\frac{d^2{\theta }_1}{d{t}^2}+\frac{1}{16\pi {\epsilon }_0{m}_1{a}^3}\left\{q_1{q}_2\frac{\cos \left(\frac{{\theta }_2-{\theta }_1}{2}\right)}{1-\cos \left({\theta }_2-{\theta }_1\right)}+q_1{q}_3\frac{\cos \left(\frac{{\theta }_3-{\theta }_1}{2}\right)}{1-\cos \left({\theta }_3-{\theta }_1\right)}\right\}\\ \frac{d^2{\theta }_2}{d{t}^2}-\frac{1}{16\pi {\epsilon }_0{m}_2{a}^3}\left\{q_1{q}_2\frac{\cos \left(\frac{{\theta }_2-{\theta }_1}{2}\right)}{1-\cos \left({\theta }_2-{\theta }_1\right)}-q_2{q}_3\frac{\cos \left(\frac{{\theta }_3-{\theta }_2}{2}\right)}{1-\cos \left({\theta }_3-{\theta }_2\right)}\right\}\\ \frac{d^2{\theta }_3}{d{t}^2}-\frac{1}{16\pi {\epsilon }_0{m}_3{a}^3}\left\{q_1{q}_3\frac{\cos \left(\frac{{\theta }_3-{\theta }_1}{2}\right)}{1-\cos \left({\theta }_3-{\theta }_1\right)}+q_2{q}_3\frac{\cos \left(\frac{{\theta }_3-{\theta }_2}{2}\right)}{1-\cos \left({\theta }_3-{\theta }_2\right)}\right\}\end{array}}$

Se resuelve el sistema de tres ecuaciones diferenciales por procedimientos numéricos con los siguientes datos: q₁=2q, q₂=2q/3, q₃=2q/5. m₁=m, m₂=2m, m₃=3m. Supondremos que la constante

${\displaystyle \frac{q^2}{16\pi {\epsilon }_{0}m{a}^3}=1}$

• Las condiciones iniciales son:

${\displaystyle \begin{array}{l}{\theta }_1=\mathrm{0,}{\theta }_2=\frac{2\pi }{3},{\theta }_3=\frac{4\pi }{3}\\ {\left(\frac{d{\theta }_1}{dt}\right)}_{t=0}=\mathrm{0,}{\left(\frac{d{\theta }_2}{dt}\right)}_{t=0}=\mathrm{0,}{\left(\frac{d{\theta }_3}{dt}\right)}_{t=0}=0\end{array}}$

parte del reposo

q1=2; m1=1;
q2=2/3; m2=2;
q3=2/5; m3=3;
% x(1) es th_1, x(2) es dth_1/dt, x(3) es th_2, x(4) es dth_2/dt, x(5) es
% th_3, x(6) es dth_3/dt
f=@(t,x) [x(2);-(q1*q2*cos((x(3)-x(1))/2)/(1-cos(x(3)-x(1)))+q1*q3*
cos((x(5)-x(1))/2)/(1-cos(x(5)-x(1))))/m1; x(4); (q1*q2*cos((x(3)-x(1))/2)
/(1-cos(x(3)-x(1)))-q2*q3*cos((x(5)-x(3))/2)/(1-cos(x(5)-x(3))))/m2; x(6);
 (q1*q3*cos((x(5)-x(1))/2)/(1-cos(x(5)-x(1)))+q2*q3*cos((x(5)-x(3))/2)
/(1-cos(x(5)-x(3))))/m3]; 
[t,x]=ode45(f,[0,80],[0,0,2*pi/3,0,4*pi/3,0]);
hold on
plot(t,x(:,1))
plot(t,x(:,3))
plot(t,x(:,5))
hold off
grid on
set(gca,'YTick',0:pi/6:3*pi/2)
set(gca,'YTickLabel',{'0','\pi/6','\pi/3','pi/2','2\pi/3','5\pi/6','\pi',
'7\pi/6','4\pi/3','3\pi/2'})
xlabel('t')
legend('\theta_1','\theta_2','\theta_3','Location','best')
ylabel('\theta');
title('Oscilaciones de las cargas')



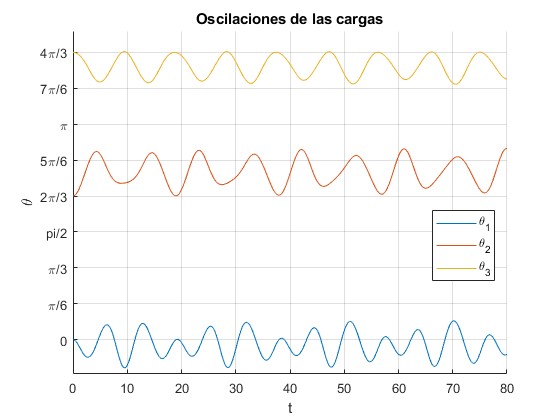
• Las condiciones iniciales son

${\displaystyle \begin{array}{l}{\theta }_1=\mathrm{0,}{\theta }_2=\frac{2\pi }{3},{\theta }_3=\frac{4\pi }{3}\\ {\left(\frac{d{\theta }_1}{dt}\right)}_{t=0}=\mathrm{1,}{\left(\frac{d{\theta }_2}{dt}\right)}_{t=0}=\mathrm{1,}{\left(\frac{d{\theta }_3}{dt}\right)}_{t=0}=1\end{array}}$

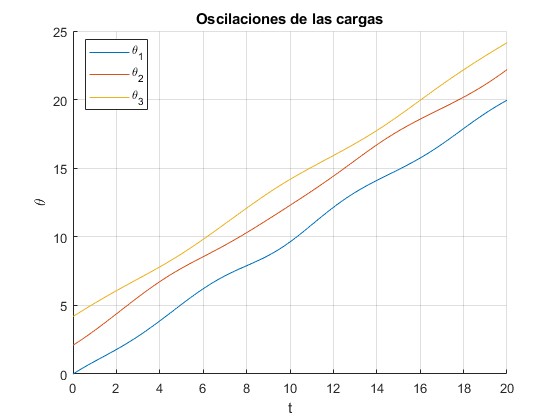
Modificamos la línea de código

...
    [t,x]=ode45(f,[0,20],[0,1,2*pi/3,1,4*pi/3,1]);
...

Referencias

J. Pierrus. Solved Problems in Classical Electromagnetism. Analytical and numerical solutions with comments. Oxford University Press (2018). Questions 2.18 y 2.19, pp. 86-89