El motor electrostático de Franklin consiste esencialmente en una rueda sin llanta que gira en el plano horizontal sobre cojinetes con un bajo coeficiente de rozamiento. Cada radio de la rueda consiste en una varilla de vidrio con un dedal de bronce en su extremo.

Para accionar el motor se guardaba una carga electrostática en una botella de Leyden, que es una versión primitiva de un condensador moderno de alta tensión. Franklin cargaba las botellas con un generador electrostático. Los terminales de dos botellas de Leyden que poseían cargas de polaridad opuesta, se situaban de manera que fuesen rozados por los dedales situados en lados opuestos de la rueda giratoria.

Desde cada terminal de la botella de Leyden saltaba una chispa al dedal que pasaba a la distancia mínima y le trasmitía una carga de la misma polaridad que la del terminal. La fuerza de repulsión entre cargas del mismo signo contribuía a proporcionar momento a la rueda. Pero también los dedales antes de cambiar de polaridad eran atraídos por el terminal de la botella de Leyden. El momento total es la suma de los momentos correspondientes a las fuerzas atractivas y repulsivas.

Existen numerosas variaciones del motor electrostático de Franklin, así como otros modelos mucho más elaborados como la máquina de Wimshurst.

El campo eléctrico de la Tierra suministra una corriente continua de intensidad relativamente pequeña a alta tensión, esta corriente puede usarse, en principio, para hacer funcionar los motores electrostáticos similares al inventado por Franklin.

Si atamos un cable a una antena situada en un globo y lo soltamos, la diferencia de potencial entre la antena y tierra aumenta a razón de 100 voltios por metro de elevación. ¿Por qué no explotar este campo para complementar las fuentes de energía tradicionales?.

Una antena situada a 20 metros suministraría alrededor de un microamperio a 2000 voltios, lo que equivale a una potencia de 0.002 vatios. Si subimos la antena, a unos 200 m la diferencia de potencial respecto de tierra del orden de 20.000 volts, pero el aire ya conduce bastante bien a esta diferencia de potencial.

Esta baja potencia es la que explica que los motores electrostáticos solamente sean un juguete para la exhibición en los museos de las ciencias.

Los motores ordinarios se basan en la fuerza que ejerce un campo magnético sobre una corriente eléctrica.

El motor electrostático

Nuestro motor está formado por 12 radios de 20 cm de longitud, de modo que el ángulo entre los radios es de 30º.

En el extremo de cada radio hay una carga puntual de valor q. Los terminales de las dos botellas de Leyden los representamos por dos cargas iguales y opuestas de valor Q.

Al girar el motor, el dedal de carga +q, roza el terminal de la botella de Leyden de carga –Q, el dedal adquiere la misma cantidad de carga pero de signo opuesto. Un proceso análogo ocurre cuando un dedal de carga –q roza el terminal de la botella de Leyden de carga +Q.

El resultado, es un cambio en el sentido de la interacción entre ambas cargas, la fuerza pasa de ser atractiva a repulsiva, lo que contribuye al momento neto respecto del eje del motor.

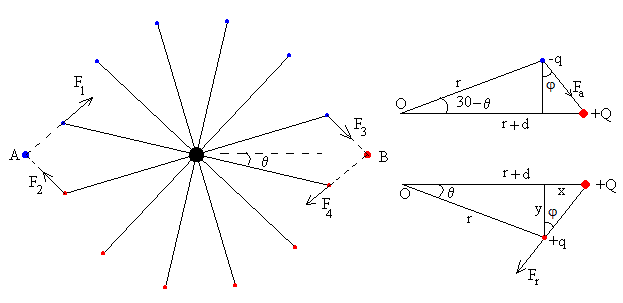
Cuando los radios del motor electrostático de Franklin han girado un ángulo θ , respecto de la posición de mínima separación con los terminales de las botellas de Leyden. La fuerza repulsiva entre la carga +Q y la carga +q vale

${\displaystyle F_r=\frac{1}{4\pi {\epsilon }_0}\frac{Qq}{x^2+y^2}}$

siendo x²+y² el cuadrado de la distancia entre las dos cargas q y Q.

y=r·sinθ
x=r+d-r·cosθ

Siendo d la mínima distancia entre las cargas puntuales q y Q, que hemos tomado como 5 cm.

${\displaystyle \tan \phi =\frac{x}{y}}$

El momento de la fuerza F_r respecto al eje del motor es

M_r=r·F_r·cos(θ-φ)

El cálculo del momento M_a de la fuerza atractiva F_a es similar al de la fuerza repulsiva, solamente hay que sustituir el ángulo θ , por 30º-θ

El momento total de las dos fuerzas atractivas y las dos repulsivas es

M=2M_a+2M_r

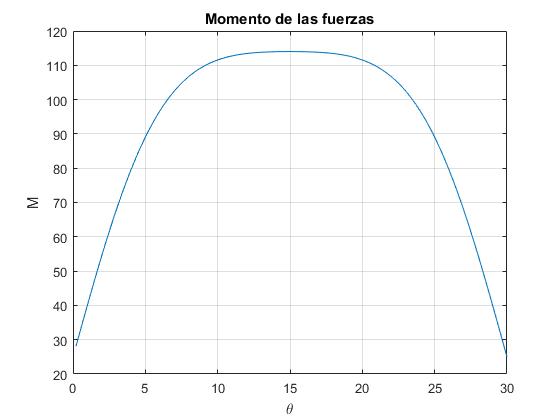
El momento será mínimo cuando las cargas q y Q estén una enfrente de la otra, y será máximo cuando θ=15º, tal como vemos en la figura de la derecha, donde se representa el momento M en función del ángulo θ

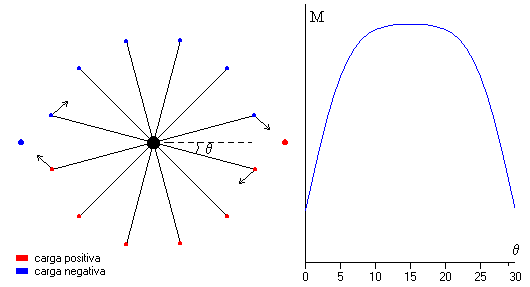
En la figura, se representa el momento de las fuerzas en función del ángulo de giro θ del radio.

R=0.2;  %radio
d=0.05; %distancia
angulo=0:0.005:pi/6;
yp=R*sin(angulo);
xp=R+d-R*cos(angulo);
m_1=R*cos(atan(xp./yp)-angulo)./(xp.^2+yp.^2);
angulo=pi/6-angulo;
yp=R*sin(angulo);
xp=R+d-R*cos(angulo);
m_2=R*cos(atan(xp./yp)-angulo)./(xp.^2+yp.^2);
plot(angulo*180/pi,2*(m_1+m_2))
grid on
xlabel('\theta');
ylabel('M')
title('Momento de las fuerzas')

La ecuación de la dinámica de rotación es

${\displaystyle I\frac{d^2\theta }{d{t}^2}=M(\theta )}$

Donde I es el momento de inercia del dispositivo respecto del eje de rotación. Se resuelve la ecuación diferencial por procedimientos numéricos con las condiciones iniciales t=0, θ=0, dθ/dt=0

p=[0.2,0.05,0.001]; %parámetros: R, d, cte
x0=[0,0]; %valores iniciales
tspan=[0 6]; 
%no pasamos nada [] en el parámetro options de ode45
[t,x]=ode45(@franklin_momento,tspan,x0,[],p);
plot(t,x(:,2))  %velocidad angular x(2)
grid on
xlabel('t')
ylabel('\omega');
title('Motor electrostático de Franklin')

function f = franklin_momento(~,x,p)
    R=p(1);
    d=p(2);
    cte=p(3); %la aceleración angular es proporcional al momento
    angulo=rem(x(1),pi/6);
    yp=R*sin(angulo);
    xp=R+d-R*cos(angulo);
    m_1=R*cos(atan(xp/yp)-angulo)/(xp^2+yp^2);
    angulo=pi/6-angulo;
    yp=R*sin(angulo);
    xp=R+d-R*cos(angulo);
    m_2=R*cos(atan(xp/yp)-angulo)/(xp^2+yp^2);
    f=[x(2); cte*2*(m_1+m_2)];
end

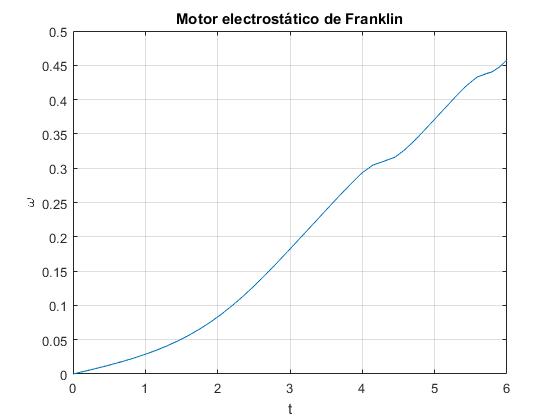
En la figura se representa la velocidad angular ω en función del tiempo t.

Ejemplo:

En la simulación se han fijado los siguientes valores de:

• la longitud de los radios r=0.2

• la distancia mínima entre los dedales de carga q y las botellas de Leyden de carga Q. d=0.05

• Las cargas q y Q son tales que

${\displaystyle \frac{qQ}{4\pi {\epsilon }_0}=1}$

1. Calculamos el momento para el ángulo θ=5º

• Momento de la fuerza de repulsión entre cargas del mismo signo



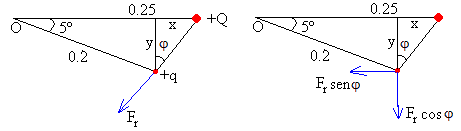
Calculamos la distancia entre las dos cargas

y=r·sinθ                        y=0.2·sin5º=0.02
x=r+d-r·cosθ                x=0.25-0.2·cos5º=0.05

La fuerza F_r de repulsión entre cargas del mismo signo vale

${\displaystyle F_r=\frac{1}{x^2+y^2}=347.1}$

tanφ=x/y  φ=71º

El momento de la fuerza de repulsión F_r respecto del origen O es la suma de los momentos de sus componentes rectangulares

(F_r·cos71)·r·cos5+ (F_r·sin71) ·r·sin5=F_r·r·cos(71-5)=28.2

• Momento de la fuerza de atracción entre cargas de distinto signo



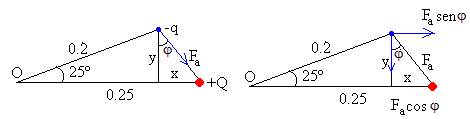
Calculamos la distancia entre las dos cargas

y=r·sinθ                       y=0.2·sin25º=0.08
x=r+d-r·cosθ                x=0.25-0.2·cos25º=0.07

La fuerza F_a de atracción entre cargas de distinto signo vale

${\displaystyle F_a=\frac{1}{x^2+y^2}=84.2}$

tanφ=x/y, φ=39º

El momento de la fuerza de atracción F_a respecto del origen O es la suma de los momentos de sus componentes rectangulares

(F_a·cos39) ·r·cos25+ (F_a·sin 39) ·r·sin25=F_a·r·cos(39-25)=16.3

El momento total es M=2(28.2+16.3)=89.1

El factor 2 se debe a que el motor consta de dos botellas de Leyden dispuestas simétricamente, los valores de los momentos calculados hay que multiplicarlos por dos.

2. El momento máximo se produce para θ=15º

El momento de la fuerza de atracción es igual al momento de la la fuerza de repulsión

y=r·sinθ                       y=0.2·sin15º=0.05
x=r+d-r·cosθ                x=0.25-0.2·cos15º=0.06

La fuerza F_a de atracción entre cargas de distinto signo vale

${\displaystyle F_a=\frac{1}{x^2+y^2}=169.3}$

El momento de la fuerza de atracción F_a respecto del origen O es la suma de los momentos de sus componentes rectangulares

F_a·cosφ·r·cos15º+F_a·sin φ ·r·sin15º=F_a·r·cos(φ-15)=28.5

donde tanφ=x/y, φ=48º

El momento total es M=2(28.5+28.5)=114.0

Actividades

El motor de Franklin es un ejemplo ilustrativo de la interacción entre cargas. Desde el punto de vista de la Mecánica, nos permite revisar el concepto de momento de una fuerza respecto de un punto, como producto de dos magnitudes: el módulo de la fuerza y el brazo o distancia de la dirección de la fuerza a dicho punto.

Las cargas positivas se representan por pequeños círculos de color rojo, las negativas por círculos de color azul.

Cuando pulsamos el botón titulado Nuevo, los radios del motor empiezan a girar. Activando el control titulado Fuerzas vemos las fuerzas de atracción y repulsión entre las cargas, cuyo momento hace girar el motor

Observamos que hay dos fuerzas atractivas y dos fuerzas repulsivas. Las fuerzas son atractivas entre cargas de distinto signo y son repulsivas entre cargas del mismo signo.

Cuando un dedal roza al correspondiente terminal de la botella de Leyden, la fuerza es máxima (ya que la distancia entre cargas es mínima), el brazo de la fuerza es cero (la dirección de la fuerza, pasa por el eje del motor) y el momento es cero.

Referencias

Stong C. L. El campo eléctrico de la tierra aporta energía a los motores electrostáticos. Investigación y Ciencia. nº 11 Agosto1977. págs 108-115.

Oleg Jefimenko Franklin's Electric Motors. Am. J. Phys. 39, October 1971, pp. 1139-1140