Caída libre antes de la apertura del paracaídas

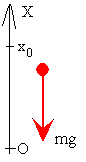
El paracaidista está sometido a la acción de su propio peso. El empuje del aire se considera despreciable ya que la densidad del aire es mucho menor que la del cuerpo. Por otra parte, consideramos que el rozamiento del paracaidista con el aire es pequeño.

Las ecuaciones del movimiento serán

${\displaystyle a=-gv=-gtx=x_0+\frac{1}{2}(-g)t^2}$

Cuando se ha abierto el paracaídas

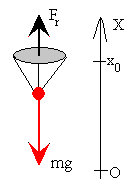
El paracaidista está sometido a la acción de su peso y de una fuerza de rozamiento proporcional al cuadrado de la velocidad.

ma=-mg+kv²

La constante de proporcionalidad $k=\frac{\rho A\delta }{2}$

• ρ es la densidad del aire. Aunque la densidad del aire varía con la altura, en este cálculo aproximado se utilizará su valor al nivel del mar de 1.29 kg/m³.
• A es el área de la sección transversal frontal expuesta al aire,
• δ es un coeficiente que depende de la forma del objeto

En la siguiente tabla, se proporcionan los coeficientes de arrastre para varios objetos

Como el paracaidista es menos aerodinámico que una esfera, pero más aerodinámico que un disco de frente, tomamos para el coeficiente de forma el promedio de los valores dados para estas dos formas en la tabla, es decir, δ=0.8.

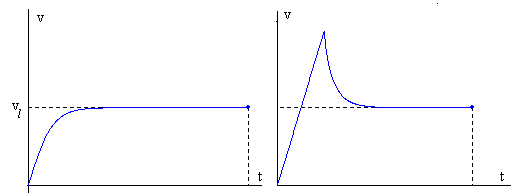
Cuando el paracaidista en caída libe abre el paracaídas, reduce bruscamente su velocidad hasta alcanzar una velocidad límite constante v_l, que se obtiene cuando el peso es igual a la fuerza de rozamiento, es decir, cuando la aceleración es cero.

-mg+kv²=0

El valor de la velocidad límite es independiente de la velocidad del paracaidista en el momento de abrir el paracaídas.

${\displaystyle v_l=\sqrt{\frac{mg}{k}}}$

Ecuación del movimiento

Escribimos la ecuación del movimiento cuando se ha abierto el paracaídas

${\displaystyle \frac{dv}{dt}=-g+\frac{k}{m}{v}^2}$

Integramos la ecuación del movimiento para obtener la velocidad v del móvil en cualquier instante t. Las condiciones iniciales son: v₀ es la velocidad del paracaidista en el instante t₀ en el que abre el paracaídas.

${\displaystyle {\displaystyle \underset{v_0}{\overset{v}{\int }}\frac{dv}{-g+\frac{k}{m}{v}^2}}={\displaystyle \underset{t_0}{\overset{t}{\int }}dt}}$

Para integrar se hace el cambio v=z·v_l.

${\displaystyle \frac{v_l}{g}{\displaystyle \underset{z_0}{\overset{z}{\int }}\frac{dz}{z^2-1}=}\frac{v_l}{2g}\left({\displaystyle \underset{z_0}{\overset{z}{\int }}\frac{dz}{z-1}-}{\displaystyle \underset{z_0}{\overset{z}{\int }}\frac{dz}{z+1}-=}\frac{v_l}{2g}\ln \frac{(z-1)(z_0+1)}{(z+1)(z_0-1)}\right)}$

Se deshace el cambio y se despeja v en función del tiempo (t-t₀), Se llega después de algunas operaciones a la expresión.

${\displaystyle v=-v_l\frac{(v_0-v_l)\exp \left(\frac{g}{v_l}(t-t_0)\right)+(v_0+v_l)\exp \left(\frac{-g}{v_l}(t-t_0)\right)}{(v_0-v_l)\exp \left(\frac{g}{v_l}(t-t_0)\right)-(v_0+v_l)\exp \left(\frac{-g}{v_l}(t-t_0)\right)}}$

Ejemplo

• Masa del paracaidista de m=72 kg,
• Área del paracaídas A=0.6 m².
• El paracaidista parte del reposo t₀=0 y abre el paracaídas v₀=0

k=(1.29·0.6·0.8)/2=0.3096

>> syms g k m v t;
>> v=dsolve('Dv=-g+k*v^2/m','v(0)=0')
v =-(g^(1/2)*m^(1/2)*tanh((g^(1/2)*k^(1/2)*t)/m^(1/2)))/k^(1/2)
>> vv=subs(v,{g,k,m},{9.8,0.3096,72});
>> ezplot(-vv,[0,40])
>> xlabel('t(s)')
>> ylabel('v(m/s)')
>> grid on
>> title('Descenso de un paracaidista')

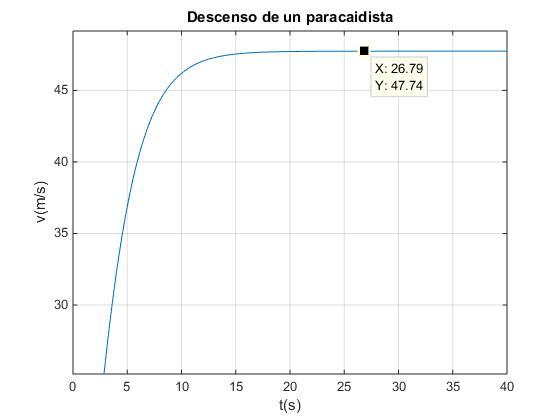
La velocidad límite constante es

${\displaystyle v=\sqrt{\frac{mg}{k}}=\sqrt{\frac{72·9.8}{0.3096}}=47.74\text{m/s}}$

Obtenemos también la expresión de la posición del móvil en función de la velocidad, haciendo un cambio de variable

${\displaystyle \frac{dv}{dt}=\frac{dv}{dx}\frac{dx}{dt}=\frac{dv}{dx}v}$

La ecuación del movimiento se transforma en

${\displaystyle v\frac{dv}{dx}=g-\frac{k}{m}{v}^2}$

Que se puede integrar de forma inmediata

${\displaystyle {\displaystyle \underset{v_0}{\overset{v}{\int }}\frac{vdv}{g-\frac{k}{m}{v}^2}}={\displaystyle \underset{x_0}{\overset{x}{\int }}dx}}$

La altura x del paracaidista en función de su velocidad v es

${\displaystyle x-x_0=\frac{v_l^2}{2g}\ln \frac{v^2-v_l^2}{v_0^2-v_l^2}}$

Despejamos la velocidad v en función de la posición x del paracaidista.

${\displaystyle v^2=v_l^2+(v_0^2-v_l^2)\exp \left(\frac{2g}{v_l^2}(x-x_0)\right)}$

Ejemplo:

• Masa del paracaidista de m=72 kg,
• Área del paracaídas A=0.6 m²
• El paracaidista parte del reposo desde la posición h=2000 m
• Abre el paracaídas en la posición x₀=1000 m, sobre el suelo.

Calcular la velocidad con la que llega al suelo

Los datos para calcular la velocidad límite v_l son:

• Densidad del aire ρ=1.29 kg/m3
• Coeficiente de forma δ =0.8

${\displaystyle k=\frac{1.29·0.6·0.8}{2}{v}_l=\sqrt{\frac{72·9.8}{k}}=47.7\text{m/s}}$

Aplicando las ecuaciones de caída de los cuerpos, calculamos la velocidad cuando el paracaidista alcanza la posición x=1000 m

1000=2000-9.8·t²/2
v=9.8·t

v=140 m/s

Esta es la velocidad inicial para la siguiente etapa del movimiento, v₀=140 m/s en la posición x₀=1000 m

La velocidad del paracaidista en la posición x=0, cuando llega al suelo, es

${\displaystyle v^2={47.7}^2+({140}^2-{47.7}^2)\exp \left(\frac{2·9.8}{{47.7}^2}(0-1000)\right)}$

v=47.7 m/s

m=72; %masa del paraciadista
area=0.6; %área del paracaídas
k=1.29*area*0.8/2;
h=2000; %altura de caida
x0=1000; %abre el paracaídas
%caída libre
x=h:-10:x0;
v2=2*(h-x)/9.8;
hold on
plot(x,sqrt(v2))
v0=sqrt(2*(h-x0)/9.8); %velocidad final de la caida libre
%abre el paracaídas
Vl=sqrt(m*9.8/k); %velocidad límite
x=x0:-10:0;
v2=Vl^2+(v0^2-Vl^2)*exp(2*9.8*(x-x0)/Vl^2);
plot(x,sqrt(v2))
hold off
xlabel('x(m)')
ylabel('v(m/s)')
title('Descenso de un paracaidista')

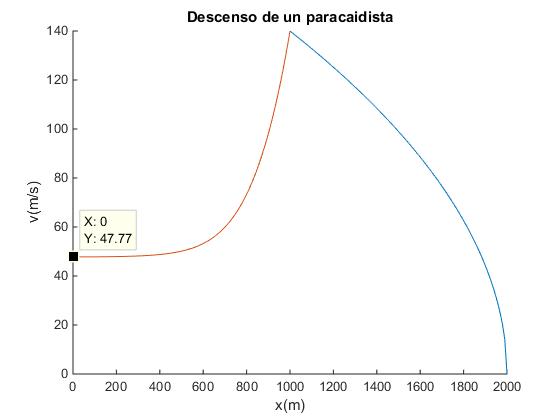
La curva de color azul representa la velocidad del paracidista en caída libre. La curva de color rosa, cuando ha abierto el paracaídas. Cuando llega al suelo ha alcanzado una velocidad próxima a la límite

Actividades

Se introduce

• La masa m del paracaidista en el control titulado Masa del paracaidista
• El área del paracaídas en el control titulado Área

Se pulsa el botón titulado Nuevo y a continuación, ►

Se pulsa el botón titulado Abre para que el paracaidista frene su caída libre al abrir el paracaídas.

El círculo rojo representa al paracaidista en caída libre, el mismo círculo rodeado de un contorno de color azul indica que ha abierto el paracaídas. Se representa las fuerzas sobre el móvil:

• En color rojo, la fuerza constante del peso.
• En color azul, la fuerza de rozamiento proporcional al cuadrado de la velocidad.

Cuando ambas flechas son iguales, la velocidad del paracaidista es constante e igual a la velocidad límite. Observar que la velocidad límite es independiente de la altura a la que abre el paracaídas.

Para determinar la dependencia del valor final de la velocidad con el peso del paracaidista y el área del paracaídas.

• Se mantiene constante el peso del paracaidista, incrementando el área del paracaídas
  
• Se mantiene constante el área del paracaídas, incrementando el peso del paracaidista.