En primer lugar, estudiamos las oscilaciones que se producen en un circuito LC

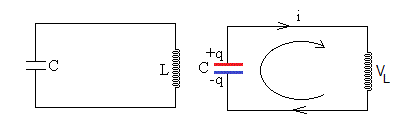
La ecuación del circuito (no hay resistencia) es

${\displaystyle \begin{array}{l}{V}_L+\frac{q}{C}=0\\ \left(-L\frac{di}{dt}\right)+\frac{q}{C}=\mathrm{0,}i=-\frac{dq}{dt}\\ \frac{d^{2}q}{d{t}^2}+\frac{1}{LC}q=0\end{array}}$

La corriente i extrae carga de la placa positiva por lo que i=-dq/dt

Obtenemos la ecuación diferencial de un Movimiento Armónico Simple (M.A.S.) de frecuencia angular propia o natural

${\displaystyle {\omega }_0=\frac{1}{\sqrt{LC}}}$

• Carga:

La solución de la ecuación diferencial es

q=Q·sin(ω₀t+φ)

donde la amplitud Q y la fase inicial φ se determinan a partir de las condiciones iniciales, la carga del condensador q₀ y la intensidad de la corriente eléctrica en el circuito i₀ en el instante inicial t=0.

• Intensidad:

Derivando la expresión de la carga q obtenemos la intensidad i

${\displaystyle i=\frac{dq}{dt}=Q{\omega }_0\cos ({\omega }_{0}t+\phi )}$

• Energía:

La energía del circuito en el instante t es la suma de la energía del campo eléctrico en el condensador y la energía del campo magnético en la bobina.

${\displaystyle E=E_E+E_B=\frac{1}{2}\frac{q^2}{C}+\frac{1}{2}L{i}^2}$

Se puede fácilmente comprobar que la suma de ambas energías es constante e independiente del tiempo.

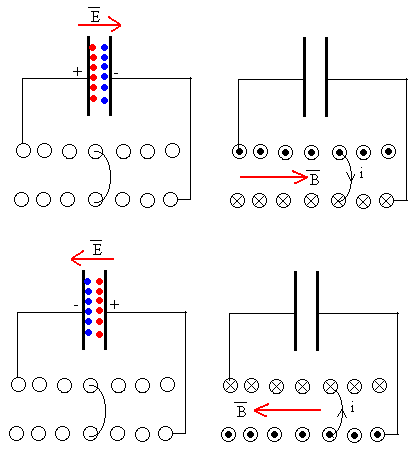
Las figuras representan el estado del oscilador cada cuarto de periodo.

1. En un instante inicial el condensador está completamente cargado con una carga Q. Toda la energía está acumulada en el condensador en forma de campo eléctrico.

2. El condensador se empieza a descargar, la intensidad aumenta, en la bobina se produce una fem autoinducida que se opone al incremento de intensidad. Al cabo de un cuarto de periodo, se alcanza la intensidad máxima i=Q·ω₀

3. La intensidad empieza a disminuir, en la bobina se produce una fem que se opone a que la intensidad disminuya. El condensador se empieza a cargar, el campo en el condensador cambia de sentido. Al cabo de un cuarto de periodo más, el condensador ha adquirido la carga máxima Q y la intensidad en la bobina se ha reducido a cero.

4. Comienza de nuevo a descargarse el condensador, la intensidad aumenta, el campo en la bobina cambia de sentido. Al cabo de un cuarto de periodo más, la intensidad alcanza su valor máximo (en valor absoluto).

5. La intensidad decrece, el condensador empieza a cargarse, el campo eléctrico en el condensador cambia de sentido. Al cabo de un cuarto de periodo más, se ha alcanzado la situación inicial de partida.

Actividades

Se introduce

• La capacidad C del condensador, en el control titulado Condensador
• La autoinducción L, en el control titulado Autoinducción
• La carga inicial del condensador se ha fijado en el programa

Se pulsa el botón titulado Nuevo

Se observa la carga del condensador, su color pasa gradualmente de rojo (carga positiva) y azul (carga negativa) a blanco (sin carga), luego se invierten gradualmente los colores. A la derecha, se traza la gráfica de la intensidad i en función del tiempo.

Circuito LCR. Oscilaciones amortiguadas

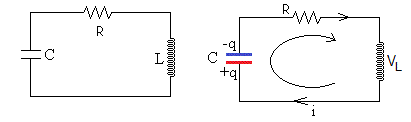
Las oscilaciones libres no se producen en un circuito real ya que todo circuito presenta una resistencia.

La ecuación del circuito es

${\displaystyle \begin{array}{l}{V}_L-\frac{q}{C}=iR\\ \left(-L\frac{di}{dt}\right)-\frac{q}{C}=iR,i=\frac{dq}{dt}\\ \frac{d^{2}q}{d{t}^2}+\frac{R}{L}\frac{dq}{dt}+\frac{1}{LC}q=0\end{array}}$

La corriente i añade carga de la placa positiva por lo que i=dq/dt

La solución de la ecuación diferencial de las oscilaciones amortiguadas es

${\displaystyle q=Q\exp (-\gamma t)\sin \left(\omega t+\phi \right){\omega }^{\text{2}}={\omega }_0^2-{\gamma }^2\gamma =\frac{R}{2L}}$

donde la amplitud Q y la fase inicial φ se determinan a partir de las condiciones iniciales, la carga del condensador q₀ y la intensidad de la corriente eléctrica en el circuito i₀ en el instante inicial t=0.

En las oscilaciones amortiguadas, la amplitud disminuye exponencialmente con el tiempo. La carga máxima del condensador va disminuyendo. La energía del sistema disminuye debido a que se disipa en la resistencia por efecto Joule.

• Cuando γ=ω₀, entonces la frecuencia de la oscilación ω =0, se denomina oscilación crítica

• Cuando γ>ω₀, entonces la frecuencia de la oscilación ω es un número imaginario, y se denomina oscilación sobreamortiguada.

Es fácil encontrar las relaciones que debe cumplir la capacidad C, resistencia R, y autoinducción L del circuito, para que se presenten los distintos casos de oscilación

• Amortiguadas
• Críticas
• Sobreamortiguadas

Circuito LCR conectado a un fem alterna. Oscilaciones forzadas

Las oscilaciones amortiguadas desaparecen al cabo de cierto tiempo, para mantener la oscilación en el circuito podemos conectarla a una fem alterna de frecuencia ω_f .

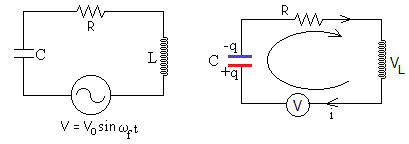
La ecuación del circuito es

${\displaystyle \begin{array}{l}{V}_L+V-\frac{q}{C}=iR\\ \left(-L\frac{di}{dt}\right)+V-\frac{q}{C}=iR,i=\frac{dq}{dt}\\ \frac{d^{2}q}{d{t}^2}+\frac{R}{L}\frac{dq}{dt}+\frac{1}{LC}q=V_0\sin \left({\omega }_{f}t\right)\end{array}}$

La corriente i añade carga de la placa positiva por lo que i=dq/dt

Ecuación similar a la estudiada para describir las oscilaciones forzadas de una masa unida a un muelle elástico.

Ejemplos

Vamos a estudiar dos ejemplos de circuitos que contienen condensadores y bobinas

Ejemplo 1

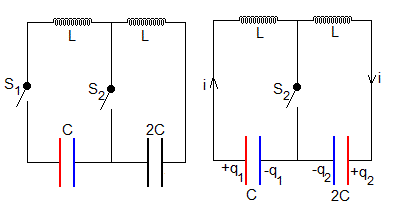
La figura muestra un circuito formado por dos condensadores de capacidades C y 2C y dos bobinas iguales de autoinducción L. En el instante t=0, el condensador C está cargado al potencial V y el condensador 2C está descargado.

Cuestión 1

Se cierra el interruptor S₁. Calculamos la carga q₁ y q₁ de cada condensador y la intensidad i

La carga inicial del condensador C es q₁₀=C·V.y la corriente inicial es nula

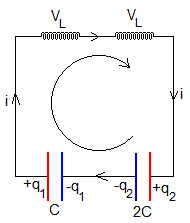
La ecuación del circuito es

${\displaystyle \begin{array}{l}2V_L-\frac{q_2}{2C}+\frac{q_1}{C}=0\\ 2\left(-L\frac{di}{dt}\right)-\frac{q_2}{2C}+\frac{q_1}{C}=\mathrm{0,}i=\frac{d{q}_2}{dt}=-\frac{d{q}_1}{dt}\end{array}}$

i=dq₂/dt, indica que la corriente i añade carga a la placa positiva del condensador 2C. i=-dq₁/dt, indica que la corriente extrae carga de la placa positiva del condensador C.

La conservación de la carga implica que, q₁+q₂=CV, que es la carga inicial.

Escribimos la ecuación diferencial en términos de q₁

${\displaystyle \begin{array}{l}2L\frac{d^2{q}_1}{d{t}^2}-\frac{CV-q_1}{2C}+\frac{q_1}{C}=0\\ \frac{d^2{q}_1}{d{t}^2}+\frac{3}{4CL}{q}_1=\frac{V}{4L}\end{array}}$

La solución particular es una constante c, tal que

${\displaystyle \frac{3}{4CL}c=\frac{V}{4L},c=\frac{CV}{3}}$

La solución de la ecuación diferencial homogénea es conocida Asin(ωt)+Bcos(ωt), con

${\displaystyle \omega =\sqrt{\frac{3}{4CL}}}$

La solución completa es

${\displaystyle \begin{array}{l}{q}_1=A\sin \left(\omega t\right)+B\cos \left(\omega t\right)+\frac{CV}{3}\\ i=-\frac{d{q}_1}{dt}=-A\omega \cos \left(\omega t\right)+B\omega \sin \left(\omega t\right)\end{array}}$

Los coeficientes A y B se determinan a partir de las condiciones iniciales

${\displaystyle \begin{array}{l}\{\begin{array}{l}CV=B+\frac{CV}{3}\\ 0=-A\omega \end{array}\\ A=\mathrm{0,}B=\frac{2}{3}CV\end{array}}$

Las cargas q₁ y q₂ y la intensidad i varían con el tiempo t de la forma

${\displaystyle \begin{array}{l}{q}_1=\frac{2}{3}CV\cos \left(\omega t\right)+\frac{1}{3}CV=\frac{1}{3}CV\left(2\cos \left(\omega t\right)+1\right)\\ q_2=CV-q_1=\frac{2}{3}CV\left(1-\cos \left(\omega t\right)\right)\\ i=\frac{d{q}_2}{dt}=\frac{2}{3}CV\sqrt{\frac{3}{4CL}}\sin \left(\omega t\right)=V\sqrt{\frac{C}{3L}}\sin \left(\omega t\right)\end{array}}$

Cuestión 2

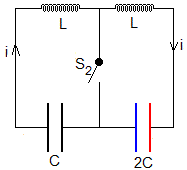
Se cierra el interruptor S₂ en el instante en el que la carga q₁ se anula. Determinar las cargas q₁ y q₂ de los condensadores y las intensidades i₁, i₂ y i₃ en función del tiempo, tomando t=0, cuando se cierra el interruptor

La carga q₁ se hace cero en el instante tal que cos(ωt)=-1/2, ωt=2π/3 (120°). La carga q₂=C·V y la intensidad $i=\frac{V}{2}\sqrt{\frac{C}{L}}$

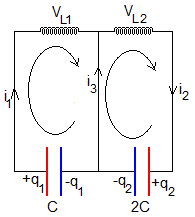
Las ecuaciones del circuito son

${\displaystyle \begin{array}{l}-L\frac{d{i}_1}{dt}+\frac{q_1}{C}=\mathrm{0,}{i}_1=-\frac{d{q}_1}{dt}\\ -L\frac{d{i}_2}{dt}-\frac{q_2}{2C}=\mathrm{0,}{i}_2=\frac{d{q}_2}{dt}\\ i_2=i_3+i_1,i_3=\frac{d{q}_1}{dt}+\frac{d{q}_2}{dt}\end{array}}$

Que se transforman en

${\displaystyle \begin{array}{l}L\frac{d^2{q}_1}{d{t}^2}+\frac{q_1}{C}=0\\ L\frac{d^2{q}_2}{d{t}^2}+\frac{q_2}{2C}=0\end{array}}$

• Solución de la primera ecuación diferencial: q₁ e i₁

${\displaystyle \begin{array}{l}{q}_1=A\sin \left({\omega }_{1}t\right)+B\cos \left({\omega }_{1}t\right),\\ i_1=-\frac{d{q}_1}{dt}=-A{\omega }_1\cos \left({\omega }_{1}t\right)+B{\omega }_1\sin \left({\omega }_{1}t\right)\end{array}\}{\omega }_1=\frac{1}{\sqrt{LC}}}$

Donde A y B se determinan a partir de las condiciones iniciales, en el instante t=0 (se cierra el interruptor S₂) q₁=0, y la intensidad $i_1=\frac{V}{2}\sqrt{\frac{C}{L}}$

${\displaystyle \begin{array}{l}\{\begin{array}{l}0=B\\ \frac{V}{2}\sqrt{\frac{C}{L}}=-A{\omega }_1\end{array}\\ \frac{V}{2}\sqrt{\frac{C}{L}}=-A\sqrt{\frac{1}{LC}},A=-\frac{CV}{2}\end{array}}$

El resultado es

${\displaystyle \begin{array}{l}{q}_1=-\frac{CV}{2}\sin \left({\omega }_{1}t\right)\\ i_1=\frac{CV}{2}{\omega }_1\cos \left({\omega }_{1}t\right)=\frac{CV}{2}\sqrt{\frac{1}{CL}}\cos \left({\omega }_{1}t\right)=\frac{V}{2}\sqrt{\frac{C}{L}}\cos \left({\omega }_{1}t\right)\end{array}}$

• Solución de la segunda ecuación diferencial: q₂ e i₂

${\displaystyle \begin{array}{l}{q}_2=A\sin \left({\omega }_{2}t\right)+B\cos \left({\omega }_{2}t\right),\\ i_2=\frac{d{q}_2}{dt}=A{\omega }_2\cos \left({\omega }_{2}t\right)-B{\omega }_2\sin \left({\omega }_{2}t\right)\end{array}\}{\omega }_2=\frac{1}{\sqrt{2LC}}}$

Donde A y B se determinan a partir de las condiciones iniciales, en el instante t=0 (se cierra el interruptor S₂) q₂=C·V, y la intensidad $i_2=\frac{V}{2}\sqrt{\frac{C}{L}}$

${\displaystyle \begin{array}{l}\{\begin{array}{l}CV=B\\ \frac{V}{2}\sqrt{\frac{C}{L}}=A{\omega }_2\end{array}\\ \frac{V}{2}\sqrt{\frac{C}{L}}=A\sqrt{\frac{1}{2LC}},A=\frac{CV}{\sqrt{2}}\end{array}}$

El resultado es

${\displaystyle \begin{array}{l}{q}_2=CV\left(\frac{1}{\sqrt{2}}\sin \left({\omega }_{2}t\right)+\cos \left({\omega }_{2}t\right)\right)=CV\sqrt{\frac{3}{2}}\sin \left({\omega }_{2}t+\phi \right),\tan \phi =\sqrt{2}\\ i_2=CV\sqrt{\frac{3}{2}}\frac{1}{\sqrt{2LC}}\cos \left({\omega }_{2}t+\phi \right)=\frac{\sqrt{3}}{2}V\sqrt{\frac{C}{L}}\cos \left({\omega }_{2}t+\phi \right)\end{array}}$

• La corriente i₃

${\displaystyle i_3=i_2-i_1=\frac{V}{2}\sqrt{\frac{C}{L}}\left\{\sqrt{3}\cos \left({\omega }_{2}t+\phi \right)-\cos \left({\omega }_{1}t\right)\right\}}$

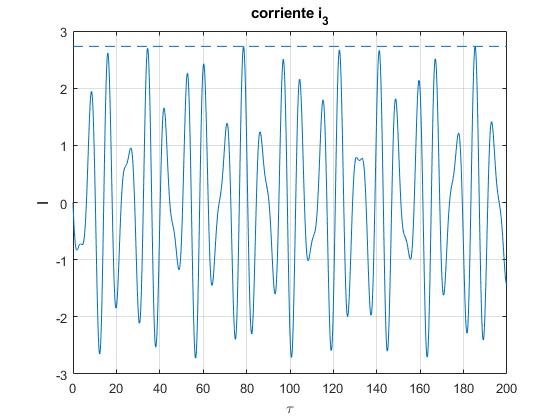
El máximo valor de la corriente es

${\displaystyle I_3=\frac{\sqrt{3}+1}{2}V\sqrt{\frac{C}{L}}}$

Representamos la corriente i₃ en unidades $\frac{V}{2}\sqrt{\frac{C}{L}}$, en función de$\frac{t}{\sqrt{LC}}$. La línea horizontal a trazos marca el máximo $\sqrt{3}+1$, del término entre corchetes

phi=atan(sqrt(2));
f=@(t) sqrt(3)*cos(t/sqrt(2)+phi)-cos(t);
fplot(f,[0,200])
line([0,200],[1+sqrt(3),1+sqrt(3)],'lineStyle','--')
grid on
ylim([-3,3])
xlabel('\tau')
ylabel('I')
title('corriente i_3')

Ejemplo 2

Sea el circuito de la figura, formado por una batería de fem V₀, dos condensadores de capacidades C y 2C y una bobina cuyo coeficiente de autoinducción es L.

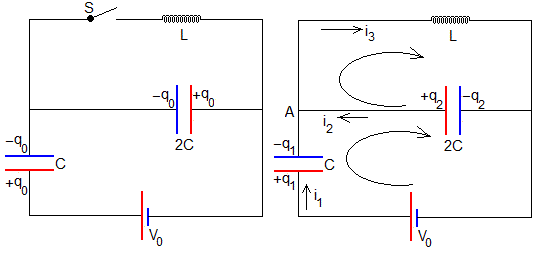
En la situación inicial, con el interruptor S abierto, la batería está unida a dos condensadores en serie. La capacidad equivalente es

${\displaystyle \frac{1}{C_e}=\frac{1}{C}+\frac{1}{2C},C_e=\frac{2}{3}C}$

Los condensadores en serie tienen la misma carga

${\displaystyle q_0=\frac{2}{3}C·V_0}$

Se cierra el circuito S, las ecuaciones del circuito (parte derecha de la figura) son

${\displaystyle \{\begin{array}{l}\left(-L\frac{d{i}_3}{dt}\right)+\frac{q_2}{2C}=0\\ V_0-\frac{q_1}{C}-\frac{q_2}{2C}=0\end{array}}$

• la intensidad i₂ extrae carga del condensador 2C, i₂=-dq₂/dt
• la intensidad i₁ añade carga al condensador C, i₁=dq₁/dt

En el nudo A las intensidades cumplen,

${\displaystyle \begin{array}{l}{i}_3=i_1+i_2\\ i_3=\frac{d{q}_1}{dt}-\frac{d{q}_2}{dt}\end{array}}$

La primera ecuación del circuito se expresa

${\displaystyle -L\frac{d^2{q}_1}{d{t}^2}+L\frac{d^2{q}_2}{d{t}^2}+\frac{q_2}{2C}=0}$

• Carga q₁ e intensidad i₁

La segunda ecuación del circuito, relaciona q₁ y q₂, q₂=2(CV₀-q₁), quedando una ecuación diferencial en q₁

${\displaystyle \frac{d^2{q}_1}{d{t}^2}+\frac{q_1}{3CL}=\frac{V_0}{3L}}$

La solución particular de la ecuación diferencial es una constante c, tal que

${\displaystyle \frac{c}{3CL}=\frac{V_0}{3L},c=C{V}_0}$

La solución de la ecuación diferencial homogénea es Asin(ωt)+Bcos(ωt). Donde A y B se determinan a partir de las condiciones iniciales. La solución completa es

${\displaystyle \begin{array}{l}{q}_1=C{V}_0+A\sin \left(\omega t\right)+B\cos \left(\omega t\right),\omega =\frac{1}{\sqrt{3CL}}\\ i_1=\frac{d{q}_1}{dt}=A\omega \cos \left(\omega t\right)-B\omega \sin \left(\omega t\right)\end{array}}$

En el instante t=0, q₁=q₀, la intensidad es nula i₁=0.

${\displaystyle \begin{array}{l}t=0\{\begin{array}{l}\frac{2}{3}C{V}_0=C{V}_0+B\\ 0=A\end{array}\\ B=-\frac{3}{3}C{V}_0\end{array}}$

La carga q₁ del condensador C y la intensidad i₁ son

${\displaystyle \begin{array}{l}{q}_1=C{V}_0-\frac{1}{3}C{V}_0\cos \left(\omega t\right),\omega =\frac{1}{\sqrt{3CL}}\\ i_1=\frac{d{q}_1}{dt}=\frac{1}{3\sqrt{3}}{V}_0\sqrt{\frac{C}{L}}\sin \left(\omega t\right)\end{array}}$

La diferencia de potencial entre las placas del condensador C es

${\displaystyle V_1=\frac{q_1}{C}=V_0\left(1-\frac{1}{3}\cos \left(\omega t\right)\right)}$

• Carga q₂ e intensidad i₂

La carga q₂ del condensador 2C y la intensidad i₂ son

${\displaystyle \begin{array}{l}{q}_2=2\left(C{V}_0-q_1\right)=\frac{2}{3}C{V}_0\cos \left(\omega t\right)\\ i_2=-\frac{d{q}_2}{dt}=\frac{2}{3\sqrt{3}}{V}_0\sqrt{\frac{C}{L}}\sin \left(\omega t\right)\end{array}}$

i₂ es el doble de i₁

La diferencia de potencial entre las placas del condensador 2C es

${\displaystyle V_2=\frac{q_2}{2C}=\frac{1}{3}{V}_0\cos \left(\omega t\right)}$

• Intensidad i₃ que pasa por la bobina

${\displaystyle i_3=i_1+i_2=\frac{1}{\sqrt{3}}{V}_0\sqrt{\frac{C}{L}}\sin \left(\omega t\right)}$

i₃ es el triple de i₁

Ejemplo

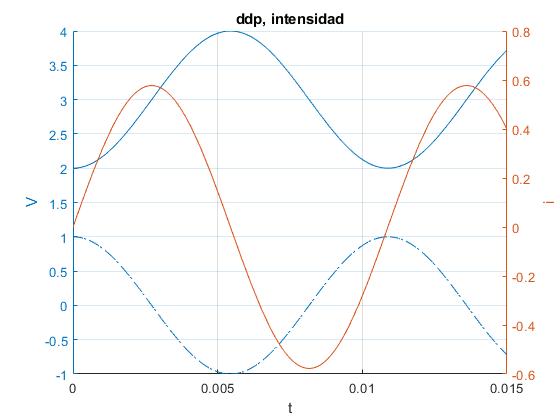
Sea V₀=3 V, C=1 mF, y L=1 mH

Representamos V₁ y V₂, diferencia de potencial entre las placas de los dos condensadores. En el mismo gráfico, representamos la intensidad i₁

C=1e-3; %capacidad
L=1e-3; %autoinducción
w=1/sqrt(3*C*L); %frecuencia angular
V0=3; %fem batería
i0=V0*sqrt(C/L)/(3*sqrt(3));
hold on
yyaxis left
fplot(@(t) V0*(1-cos(w*t)/3),[0,15/1000]) %V1
fplot(@(t) V0*cos(w*t)/3,[0,15/1000]) %V2
yyaxis right
fplot(@(t) i0*sin(w*t),[0,15/1000]) %i1
hold off
xlabel('t')
yyaxis left
ylabel('V')
yyaxis right
ylabel('i')
grid on
title('ddp, intensidad')

Referencias

Physics Challenge for Teachers and Students. An amplitude with an attitude. The Physics Teacher, Vol. 59, April 2021. pp. 302
Solution to the April, 2021 Challenge. The Physics Teacher, 59, 09, June 2021, AB382

Physics Challenge for Teachers and Students. May the charge grow large. The Physics Teacher, Vol. 58, May 2020. pp. 359
Solution to the April, 2021 Challenge. The Physics Teacher, Phys. Teach. 58, A444 (2020)