Fuerza de rozamiento proporcional a la velocidad y al cuadrado de la velocidad
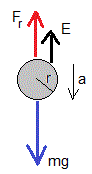
Sea una esfera de radio r, densidad ρs que se deja caer en el seno de un fluido de densidad ρf y viscosidad η. Las fuerzas sobre la esfera son
- El peso, mg
- El empuje, E
- La fuerza de rozamiento, Fr
La ecuación del movimiento es
La aceleración de la gravedad efectiva es
La fórmula de Stokes, fuerza de rozamiento proporcional a la velocidad es
La fuerza de rozamiento proporcional al cuadrado de la velocidad. Para una esfera el coeficiente de arrastre, CD=0.4
Velocidad de caída de la esfera
Supondremos que la esfera parte del reposo, integramos la ecuación del movimiento
Teniendo en cuenta la relación
La velocidad tiende a un valor límite constante, v∞ cuando t→∞
Expresamos la velocidad en términos de otro parámetro, k
Teniendo en cuenta esta relación, llegamos a la expresión final de la velocidad v
Comprobamos que para t=0, v=0
Casos particulares
Fuerza de rozamiento proporcional al cuadrado de la velocidad, b=0, k=0
Fuerza de rozamiento proporcional a la velocidad, c=0, k=∞
Aplicamos la regla de L'Hôpital, para los límites indeterminados ∞/∞ y 0/0
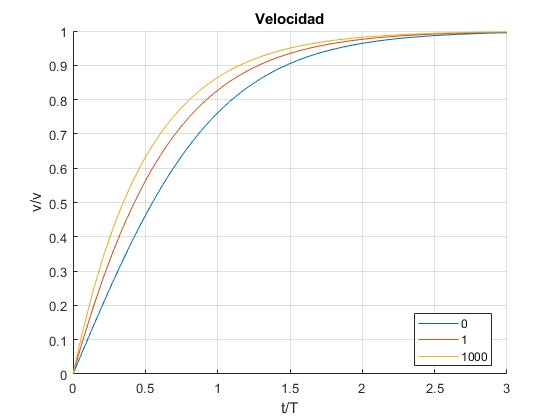
Representamos el cociente v/v∞ para tres valores del parámtero k, 0, 1, 1000 (infinito)
hold on
for k=[0,1,1000]
v=@(t) 1-(2+2*k)./((1+2*k)*exp(2*t)+1);
fplot(v,[0,3])
end
hold off
grid on
xlabel('t/T')
ylabel('v/v_')
legend('0','1','1000','location','best')
title('Velocidad')
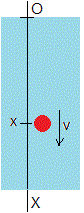
Altura de la esfera
Integramos la expresión de la velocidad, para obtener la altura x en función del tiempo t. Supondremos que la esfera parte del origen y el eje X apunta hacia abajo
Resolvemos la integral
El resultado es
Casos particulares
Fuerza de rozamiento proporcional al cuadrado de la velocidad, b=0, k=0
Fuerza de rozamiento proporcional a la velocidad, c=0, k=∞
Utilizamos Math Symbolic de MATLAB para calcular el límite de la expresión.
>> syms a k; >> limit((1+k)*log((2*k+1+a)/(2*k+2)),k,inf) ans =a/2 - 1/2
El resultado es
Resultados
Régimen lineal, k·v
Se ha utilizado una esfera de r=1.5 mm de radio, de densidad, ρs=1130 kg/m3. La densidad del líquido es ρf=920 kg/m3 y su viscosidad η= 70 mPa·s
Las medidas de la altura de la esfera x en función del tiempo t son
| t (s) | 0.672 | 1.130 | 1.672 | 2.145 | 2.664 | 3.160 | 3.664 | 4.153 | 4.687 | 5.191 | 5.702 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| x (cm) | 0.768 | 1.536 | 2.304 | 3.532 | 4.300 | 5.068 | 5.836 | 6.604 | 7.833 | 9.215 | 10.290 |
Representamos la función x(t) y los datos experimentales
t=[0.672, 1.130, 1.672, 2.145, 2.664, 3.160, 3.664, 4.153, 4.687, 5.191,
5.702];
y=[0.768, 1.536, 2.304, 3.532, 4.300, 5.068, 5.836, 6.604, 7.833, 9.215,
10.290];
r=1.5e-3; %radio
rho_s=1130; %densidad esfera
rho_f=920; %densidad líquido
eta=70e-3; %viscosidad
ge=9.8*(1-rho_f/rho_s); %gravedad efectiva
b=9*eta/(2*rho_s*r^2);
c=3*rho_f/(20*rho_s*r);
T=2/sqrt(4*c*ge+b^2);
v_lim=1/(c*T)-b/(2*c);
k=b*T/(2-b*T);
hold on
plot(t,y,'ro','markersize',3,'markerfacecolor','r')
x=@(t) v_lim*(t+(1+k)*T*log((2*k+1+exp(-2*t/T))/(2*k+2)))*100; %en cm
fplot(x,[0,5])
hold off
grid on
xlabel('t (s)')
ylabel('x (cm)')
title('Altura')
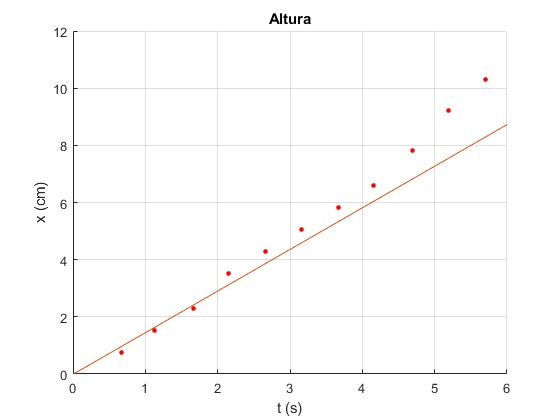
El número de Reynolds Re=0.57 cuando la esfera ha alcanzado ha alcanzado la velocidad límite constante
>> Re=rho_f*2*r*v_lim/eta >>0.5741
Régimen cuadrático, k·v2
Se ha utilizado una esfera de r=2.38 mm de radio, de densidad, ρs=7800 kg/m3. La densidad del líquido es ρf=1000 kg/m3 y su viscosidad η= 0.98 mPa·s
Las medidas de la altura de la esfera x en función del tiempo t son
| t (s) | 0.041 | 0.091 | 0.142 | 0.193 | 0.243 |
|---|---|---|---|---|---|
| x (cm) | 0.685 | 2.900 | 6.591 | 10.808 | 14.921 |
Representamos la función x(t) y los datos experimentales
t=[0.041, 0.091, 0.142, 0.193, 0.243];
y=[0.685, 2.900, 6.591, 10.808, 14.921];
r=2.38e-3; %radio
rho_s=7800; %densidad esfera
rho_f=1000; %densidad líquido
eta=0.98e-3; %viscosidad
ge=9.8*(1-rho_f/rho_s); %gravedad efectiva
b=9*eta/(2*rho_s*r^2);
c=3*rho_f/(20*rho_s*r);
T=2/sqrt(4*c*ge+b^2);
v_lim=1/(c*T)-b/(2*c);
k=b*T/(2-b*T);
hold on
plot(t,y,'ro','markersize',3,'markerfacecolor','r')
x=@(t) v_lim*(t+(1+k)*T*log((2*k+1+exp(-2*t/T))/(2*k+2)))*100; %en cm
fplot(x,[0,0.25])
hold off
grid on
xlabel('t (s)')
ylabel('x (cm)')
title('Altura')
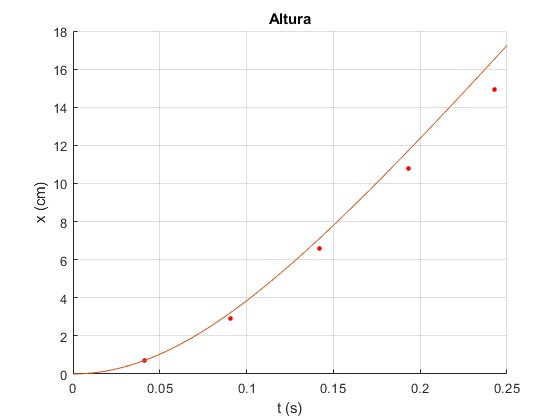
El número de Reynolds Re=4 964 cuando la esfera ha alcanzado la velocidad límite constante
>> Re=rho_f*2*r*v_lim/eta >>4.9646e+03
Régimen intermedio
Se ha utilizado una esfera de r=2.38 mm de radio, de densidad, ρs=7800 kg/m3. La densidad del líquido es ρf=920 kg/m3 y su viscosidad η=70 mPa·s
Las medidas de la altura de la esfera x en función del tiempo t son
| t (s) | 0.024 | 0.051 | 0.076 | 0.101 | 0.125 | 0.151 | 0.175 |
|---|---|---|---|---|---|---|---|
| x (cm) | 0.256 | 0.872 | 1.865 | 2.692 | 3.923 | 5.026 | 6.231 |
Representamos la función x(t) y los datos experimentales
t=[0.024, 0.051, 0.076, 0.101, 0.125, 0.151, 0.175];
y=[0.256, 0.872, 1.865, 2.692, 3.923, 5.026, 6.231];
r=2.38e-3; %radio
rho_s=7800; %densidad esfera
rho_f=920; %densidad líquido
eta=70e-3; %viscosidad
ge=9.8*(1-rho_f/rho_s); %gravedad efectiva
b=9*eta/(2*rho_s*r^2);
c=3*rho_f/(20*rho_s*r);
T=2/sqrt(4*c*ge+b^2);
v_lim=1/(c*T)-b/(2*c);
k=b*T/(2-b*T);
hold on
plot(t,y,'ro','markersize',3,'markerfacecolor','r')
x=@(t) v_lim*(t+(1+k)*T*log((2*k+1+exp(-2*t/T))/(2*k+2)))*100; %en cm
fplot(x,[0,0.20])
hold off
grid on
xlabel('t (s)')
ylabel('x (cm)')
title('Altura')
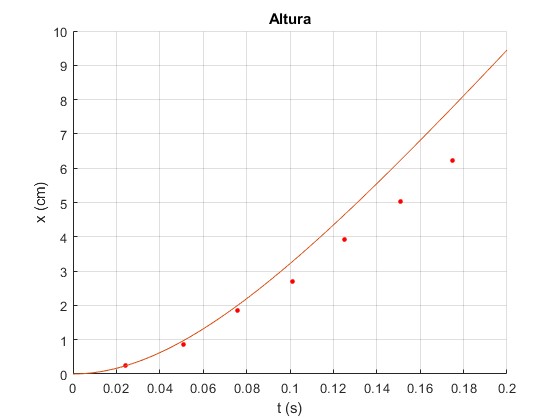
El número de Reynolds Re=44 cuando la esfera ha alcanzado la velocidad límite constante
>> Re=rho_f*2*r*v_lim/eta >>43.8308
Los datos experimentales no se ajustan al modelo de fuerza de rozamiento descrito en esta página
Otro modelo de fuerza de rozamiento
Existen fórmulas que describen con mayor o menor aproximación las medidas del coeficiente de arrastre CD para un objeto de forma esférica en un amplio intervalo de números de Reynolds, Re.
El modelo de fuerza de rozamiento descrito en esta página, Fr=mbv+mcv2, corresponde a la siguiente coeficiente de arrastre CD
De la definición de número de Reynolds, Re
Representamos los coeficientes CD en función del número de Reynolds, Re
c1=@(x) 24./x+2.6*(x/5.0)./(1+(x/5.0).^1.52)+
0.411*((x/263000).^-7.94)./(1+(x/263000).^-8.00)+0.25*(x/1e6)/(1+x/1e6);
c2=@(x) 24./x+0.4;
re=logspace(-2,6,100);
loglog(re,c1(re),re,c2(re))
grid on
xlabel('Re')
ylabel('C_D')
title('Coeficiente C_D de arrastre')
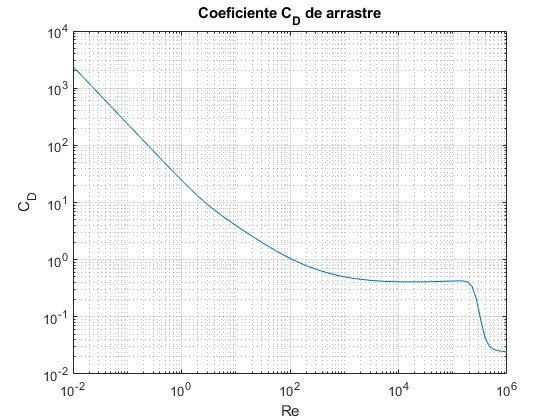
No hay mucha diferencia, entre el primero (en azul) y el segundo (en rojo), excepto a valores intermedios del número de Reynolds
La fuerza de rozamiento vale
La ecuación del movimiento se escribe
Donde el coeficiente de arrastre CD no es constante, sino una función del número de Reynolds, Re, que a su vez, depende de la velocidad v
Resolvemos la ecuación diferencial por el procedimiento numérico
Consideremos de nuevo el tercer caso (régimen intermedio). Representamos la altura de la esfera x en cm en función del tiempo t en s. Representamos los datos experimentales de la tercera tabla
function roza_fluidos_4
tt=[0.024, 0.051, 0.076, 0.101, 0.125, 0.151, 0.175];
y=[0.256, 0.872, 1.865, 2.692, 3.923, 5.026, 6.231];
r=2.38e-3; %radio
rho_s=7800; %densidad esfera
rho_f=920; %densidad líquido
eta=70e-3; %viscosidad
ge=9.8*(1-rho_f/rho_s); %gravedad efectiva
[t,x]=ode45(@fuerza,[0,0.175],[0,eps]);
hold on
plot(t,x(:,1)*100)
plot(tt,y,'ro','markersize',3,'markerfacecolor','r')
hold off
grid on
xlabel('t (s)')
ylabel('x (cm)')
title('Altura')
function tp=Re(v)
tp=2*rho_f*r*v/eta;
end
function dr=fuerza(~, x)
dr=zeros(2,1);
cD=@(v) 24./Re(v)+2.6*(Re(v)/5.0)./(1+(Re(v)/5.0).^1.52)+0.411*
((Re(v)/263000).^-7.94)./(1+(Re(v)/263000).^-8.00)+0.25*(Re(v)/1e6)/(1+Re(v)/1e6);
dr(1)=x(2);
dr(2)=ge-3*cD(x(2))*rho_f*x(2)^2/(8*r*rho_s);
end
end
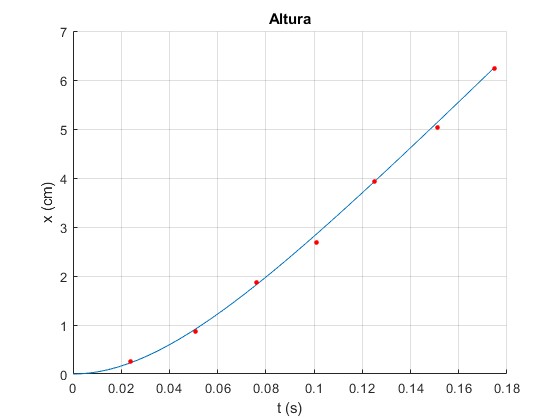
El ajuste entre el modelo de fuerza de rozamiento descrito y los datos experimentales es muy bueno
Nota, si la velocidad inicial es nula, se produce un error por división entre cero. Para evitarlo, se sustituye 0 por
Referencias
Aldo Mayme, Carl E Mungan. Vertical fall of a sphere opposed by fluid buoyancy and drag. Eur. J. Phys. 46 (2025) 035004

