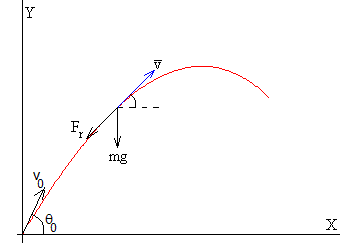
Un proyectil de masa m se dispara desde el origen con velocidad v₀, haciendo un ángulo θ₀ con la horizontal

Las componentes de la velocidad inicial son

v_0x=v₀·cosθ
v_0y=v₀·sinθ

Si despreciamos el empuje, las fuerzas que actúan sobre el cuerpo de masa m son:

• El peso mg
• La fuerza de rozamiento F_r, que es sentido contrario al vector velocidad (tangente a la trayectoria). $\overrightarrow{F_r}=-mb\overrightarrow{v}$

Las ecuaciones del movimiento del cuerpo serán por tanto.

${\displaystyle \begin{array}{l}m\frac{d{v}_x}{dt}=-mb{v}_x\\ m\frac{d{v}_y}{dt}=-mg-mb{v}_y\end{array}}$

La solución de estas ecuaciones con las condiciones iniciales t=0, v_x=v_0x, v_y=v_0y, son

${\displaystyle \begin{array}{l}{\displaystyle \underset{v_{0x}}{\overset{v_x}{\int }}\frac{d{v}_x}{v_x}=-b}{\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ \ln v_x-\ln v_{0x}=-bt\\ v_x=v_{0x}\exp (-bt)\\ {\displaystyle \underset{v_{0y}}{\overset{v_y}{\int }}\frac{d{v}_y}{g+b{v}_y}=-}{\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ \frac{1}{b}\left(\ln \left(g+b{v}_y\right)-\ln \left(g+b{v}_{0y}\right)\right)=-t\\ v_y=\left(\frac{g}{b}+v_{0y}\right)\exp (-bt)-\frac{g}{b}\end{array}}$

Integrando de nuevo, con las condiciones iniciales t=0, x=0, y=0, tenemos

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{x}{\int }}dx}={\displaystyle \underset{0}{\overset{t}{\int }}\left(v_{0x}\exp (-bt)\right)dt}\\ x=\frac{v_{0x}}{b}\left(1-\exp (-bt)\right)\\ {\displaystyle \underset{0}{\overset{x}{\int }}dy}={\displaystyle \underset{0}{\overset{t}{\int }}\left(\left(\frac{g}{b}+v_{0y}\right)\exp (-bt)-\frac{g}{b}\right)dt}\\ y=\frac{1}{b}\left(\frac{g}{b}+v_{0y}\right)\left(1-\exp (-bt)\right)-\frac{g}{b}t\end{array}}$

Alcance del proyectil y tiempo de vuelo

El proyectil llega al suelo y=0, a una distancia x=R del origen. R se denomina alcance del proyectil.

En la primera ecuación, ponemos x=R y despejamos el tiempo de vuelo t,

${\displaystyle t=-\frac{1}{b}\ln \left(1-\frac{Rb}{v_{0x}}\right)}$

sustituyéndola en la segunda ecuación con y=0.

${\displaystyle \left(\frac{g}{b}+v_{0y}\right)\frac{R}{v_{0x}}+\frac{g}{b^2}\ln \left(1-\frac{Rb}{v_{0x}}\right)=0}$

Esta es una ecuación transcendente en R, que se resolverá por procedimientos numéricos

Representamos el alcance R en función del ángulo de tiro θ₀ para la velocidad de disparo v₀=60 m/s. El parámetro de la fuerza de rozamiento b=0.05 s^-1

b=0.05; %parámetro
v0=60;  %velocidad incial
R=zeros(1,70);
i=0;
for angulo=(10:80)*pi/180 %ángulos de tiro
    i=i+1;
    v0x=v0*cos(angulo);
    v0y=v0*sin(angulo);
    f=@(x) (9.8/b+v0y)*x/v0x+9.8*log(1.0-x*b/v0x)/b^2;
    R0=v0^2*sin(2*angulo)/9.8; %alcance sin rozamiento
    R(i)=fzero(f,R0);  %alcance 
end
plot(10:80,R)
grid on
ylabel('Alcance (m)')
xlabel('\theta')
title('Tiro parabólico con rozamiento')

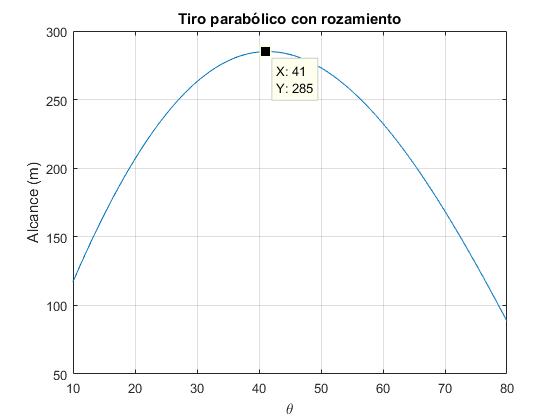
El alcance máximo ya no se produce para el ángulo θ=45°

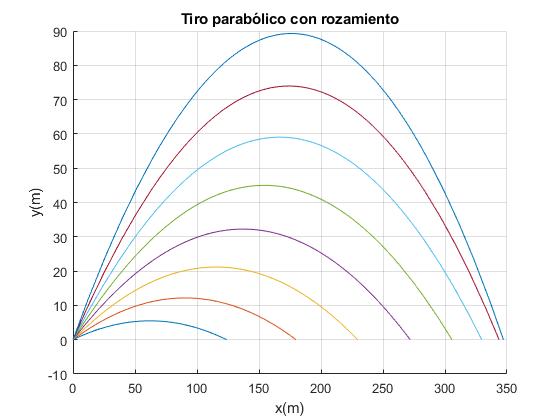
Representamos las trayectorias de proyectiles disparados con la misma velocidad inicial v₀ y con ángulos de tiro θ de 10, 15, 20, 25, 30, 35, 40 y 45°

b=0.01; %parámetro
v0=60;  %velocidad incial

hold on
for angulo=(10:5:45)*pi/180
    v0x=v0*cos(angulo);
    v0y=v0*sin(angulo);

    f=@(x) (9.8/b+v0y)*x/v0x+9.8*log(1.0-x*b/v0x)/b^2;
    R0=v0^2*sin(2*angulo)/9.8; %sin rozamiento
    R=fzero(f,R0);  %alcance 
    T=-log(1-b*R/v0x)/b; %tiempo de vuelo
    fplot(@(t) v0*cos(angulo)*(1-exp(-b*t))/b, @(t) (9.8/b^2+v0*sin(angulo)/b)
*(1-exp(-b*t))-9.8*t/b,[0,T]);
end
grid on
hold off
xlabel('x(m)')
ylabel('y(m)')
title('Tiro parabólico con rozamiento')

Aproximaciones

Si la resistencia del aire es pequeña b~0, el término ln(1-bR/v_0x) se puede desarrollar en serie hasta potencias de tercer orden en b en la ecuación trascendente

${\displaystyle \begin{array}{l}\ln \left(1-\frac{bR}{v_{0x}}\right)\approx \ln (1)+{\frac{1}{1!}\frac{-R/v_{0x}}{1-bR/v_{0x}}|}_{b=0}b+{\frac{1}{2!}\frac{-R^2/v_{0x}^2}{{\left(1-bR/v_{0x}\right)}^2}|}_{b=0}{b}^2\\ +{\frac{1}{3!}\frac{-2R^3/v_{0x}^3}{{\left(1-bR/v_{0x}\right)}^3}|}_{b=0}{b}^3=-\frac{R}{v_{0x}}b-\frac{1}{2}\frac{R^2}{v_{0x}^2}{b}^2-\frac{1}{3}\frac{R^3}{v_{0x}^3}{b}^3\end{array}}$

Haciendo algunas operaciones obtenemos la ecuación de segundo grado en R

${\displaystyle \frac{2b}{3v_0\cos \theta }{R}^2+R-R_0=0R_0=\frac{2v_{0x}{v}_{0y}}{g}=\frac{v_0^2\sin (2\theta )}{g}}$

Donde R₀ es el alcance cuando no se considera el rozamiento del aire.

Ejemplo: Sea v₀=60 m/s, θ=45º y b=0.01

v0=60; %velocidad inicial
g=9.8; %aceleración de la gravedad
b=0.01; %rozamiento proporcional a la velocidad
angulo=pi/4; %45º
v0x=v0*cos(angulo);
v0y=v0*sin(angulo);
f=@(x) (9.8/b+v0y)*x/v0x+9.8*log(1.0-x*b/v0x)/b^2;
R0=v0^2*sin(2*angulo)/9.8; %sin rozamiento
R=fzero(f,R0);  %alcance con rozamiento 
%aproximación
Ra=(-1+sqrt(1+8*R0*b/(3*v0x)))/(4*b/(3*v0x));
fprintf('ideal %3.2f, exacto %3.2f, aproximado %3.2f\n',R0,R,Ra)

ideal 367.35, exacto 347.16, aproximado 348.29

Cuando hay un pequeño rozamiento con el aire b=0.01, el alcance aproximado se obtiene resolviendo la ecuación de segundo grado en R, cuya raíz positiva es R=348.29 m

Tiempo de vuelo y alcance. Solución analítica

El tiempo de vuelo es el tiempo que tarda el proyectil desde que es disparado hasta que llega al suelo y=0.

${\displaystyle \begin{array}{l}y=\frac{1}{b}\left(\frac{g}{b}+v_{0y}\right)\left(1-\exp (-bt)\right)-\frac{g}{b}t\hfill \\ \begin{array}{l}\frac{g}{b}+v_0\sin \theta -gt=\left(\frac{g}{b}+v_0\sin \theta \right)\exp (-bt)\hfill \\ e^{-bt}=-\frac{g}{\frac{g}{b}+v_0\sin \theta }t+1\hfill \end{array}\hfill \end{array}}$

Se trata de un caso particular de la ecuación a^b·x+c=d·x+f, cuya solución se expresa en términos de la función W de Lambert

${\displaystyle x=\frac{-1}{b\ln a}W\left(\frac{-b}{d}\left(\ln a\right)a^{c-bf/d}\right)-\frac{f}{d}}$

Haciendo la sustitución

${\displaystyle \begin{array}{l}x\to t\\ a\to e\\ b\to -b\\ c\to 0\\ d\to -\frac{g}{\frac{g}{b}+v_0\sin \theta }\\ f\to 1\end{array}}$

El tiempo t de vuelo es exactamente

${\displaystyle \begin{array}{l}t=\frac{1}{b}\left(-u+W\left(u{e}^u\right)\right)\\ u=-1-\frac{b{v}_0}{g}\sin \theta \end{array}}$

Dado el tiempo de vuelo t, calculamos el alcance x del proyectil que denominamos R

${\displaystyle R=\frac{v_0\cos \theta }{b}\left(1-\exp \left(u-W\left(u{e}^u\right)\right)\right)}$

Teniendo en cuenta que z=W(z)exp(W(z)), con z=ue^u, el alcance R es

${\displaystyle R=\frac{v_0\cos \theta }{b}\left(1-\frac{W\left(u{e}^u\right)}{u}\right)}$

En el apartado anterior, calculamos, utilizando procedimientos numéricos, el valor aproximado del alcance R, obteniendo una gráfica similar del alcance del proyectil R en función del ángulo de tiro θ, fijada la velocidad de disparo v₀ y la constante de proporcionalidad b de la fuerza de rozamiento. Ahora, realizamos un cálculo exacto utilizando la función W de Lambert

b=0.05; %parámetro
v0=60;  %velocidad incial
R=zeros(1,70);
i=0;
for angulo=(10:80)*pi/180
    i=i+1;
    u=-1-b*v0*sin(angulo)/9.8;
    R(i)=(v0*cos(angulo)/b)*(1-lambertw(0,u*exp(u))/u); %alcance 
end
plot(10:80,R)
grid on
ylabel('Alcance (m)')
xlabel('\theta')
title('Tiro parabólico con rozamiento')

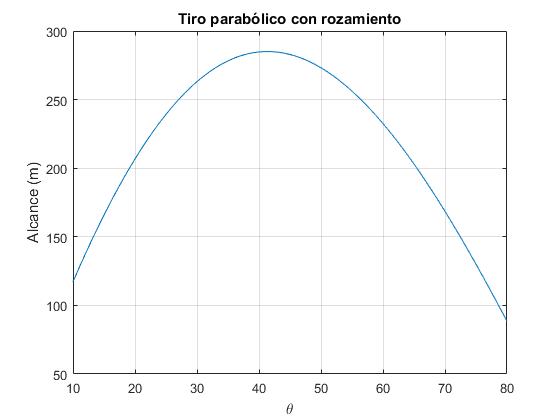
>> [M,I]=max(R)
M =  285.0226
I =    32 %índice
>> ang=10:80;
>> ang(I)
ans =    41

El alcance máximo R_m=285.0 m se produce para el ángulo de tiro óptimo θ_m=41°

Ejemplo: Sea v₀=60 m/s, θ=45º y b=0.01

v0=60; %velocidad inicial
g=9.8; %aceleración de la gravedad
b=0.01; %rozamiento proporcional a la velocidad
angulo=pi/4; %45º
u=-1-b*v0*sin(angulo)/g;
R=(v0*cos(angulo)/b)*(1-lambertw(0,u*exp(u))/u); %alcance 
disp(R)

347.1646

El mismo valor que obtuvimos empleando procedimientos numéricos

Trabajo y energía

Definimos la velocidad v_t=g/b. Que es la velocidad límite constante dv_y/dt=0, en el movimiento vertical

• Variación de energía potencial

${\displaystyle \begin{array}{l}\Delta E_p=mgy=m\left\{\frac{g}{b}\left(\frac{g}{b}+v_{0y}\right)\left(1-\exp (-bt)\right)-\frac{g^2}{b}t\right\}\\ \Delta E_p=m\left\{v_t\left(v_t+v_{0y}\right)\left(1-\exp \left(-\frac{g}{v_t}t\right)\right)-v_{t}gt\right\}\end{array}}$

• Variación de energía cinética

${\displaystyle \begin{array}{l}\Delta E_k=\frac{1}{2}m{v}^2-\frac{1}{2}m{v}_0^2=\frac{1}{2}m\left(v_x^2+v_y^2\right)=\frac{1}{2}m\left(v_{0x}^2\exp (-2bt)+{\left(\left(\frac{g}{b}+v_{0y}\right)\exp (-bt)-\frac{g}{b}\right)}^2\right)=\\ =\frac{1}{2}m\left\{\left(v_0^2+v_t^2+2v_{0y}{v}_t\right)\exp \left(-\frac{2g}{v_t}t\right)+v_t^2-2v_t\left(v_{0y}+v_t\right)\exp \left(-\frac{g}{v_t}t\right)-v_0^2\right\}\end{array}}$

La energía cinética tiende hacia un valor constante

La suma es

${\displaystyle \begin{array}{l}\Delta E=\Delta E_k+\Delta E_p=\\ m\left\{\frac{1}{2}\left(v_0^2+v_t^2+2v_t{v}_{0y}\right)\exp \left(-\frac{2g}{v_t}t\right)-g{v}_{t}t-2v_t\left(v_t+v_{0y}\right)\exp \left(-\frac{g}{v_t}t\right)-\frac{v_0^2}{2}+\frac{3}{2}{v}_t^2+v_t{v}_{0y}\right\}\end{array}}$

• Trabajo de la fuerza de rozamiento

${\displaystyle \begin{array}{l}W=-{\displaystyle \underset{0}{\overset{t}{\int }}mb{v}^{2}dt=}-mb{\displaystyle \underset{0}{\overset{t}{\int }}\left\{v_{0x}^2\exp (-2bt)+{\left(\left(\frac{g}{b}+v_{0y}\right)\exp (-bt)-\frac{g}{b}\right)}^2\right\}dt=}\\ -mb\left\{-\frac{1}{2b}\left(v_0^2+\frac{g^2}{b^2}+2\frac{g}{b}{v}_{0y}\right)\exp (-2bt)+\frac{g^2}{b^2}t+2\frac{g}{b^2}\left(\frac{g}{b}+v_{0y}\right)\exp (-bt)+\frac{v_0^2}{2b}-\frac{3}{2}\frac{g^2}{b^3}-\frac{g}{b^2}{v}_{0y}\right\}=\\ m\left\{\frac{1}{2}\left(v_0^2+v_t^2+2v_t{v}_{0y}\right)\exp \left(-2bt\right)-g{v}_{t}t-2v_t\left(v_t+v_{0y}\right)\exp \left(-bt\right)-\frac{v_0^2}{2}+\frac{3}{2}{v}_t^2+v_t{v}_{0y}\right\}\end{array}}$

El trabajo de la fuerza de rozamiento es igual a la variación de energía (cinética más potencial)

Llamando $\tau =\frac{gt}{v_t}=bt$, el trabajo de la fuerza de rozamiento, la variación de energía cinética y la variación de energía potencial, en unidades de la energía cinética inicial

${\displaystyle \begin{array}{l}\frac{W}{\frac{1}{2}m{v}_0^2}=\left(1+\frac{v_t^2}{v_0^2}+2\frac{v_t}{v_0}\sin \theta \right)\exp \left(-2\tau \right)-2\frac{v_t^2}{v_0^2}\tau -4\frac{v_t}{v_0}\left(\frac{v_t}{v_0}+\sin \theta \right)\exp \left(-\tau \right)-1+3\frac{v_t^2}{v_0^2}+2\frac{v_t}{v_0}\sin \theta \\ \frac{\Delta E_k}{\frac{1}{2}m{v}_0^2}=\left(1+\frac{v_t^2}{v_0^2}+2\frac{v_t}{v_0}\sin \theta \right)\exp \left(-2\tau \right)+\frac{v_t^2}{v_0^2}-2\frac{v_t}{v_0}\left(\frac{v_t}{v_0}+\sin \theta \right)\exp \left(-\tau \right)-1\\ \frac{\Delta E_p}{\frac{1}{2}m{v}_0^2}=2\left\{\frac{v_t}{v_0}\left(\frac{v_t}{v_0}+\sin \theta \right)\left(1-\exp \left(-\tau \right)\right)-\frac{v_t^2}{v_0^2}\tau \right\}\end{array}}$

El tiempo de vuelo se calcula cuando y=0. Expresamos la ecuación trascendente en términos de las magnitudes adimensionales τ y v_t/v₀

${\displaystyle \begin{array}{l}\frac{1}{b}\left(\frac{g}{b}+v_{0y}\right)\left(1-\exp (-bt)\right)-\frac{g}{b}t=0\\ v_t\left(v_t+v_{0y}\right)\left(1-\exp (-\tau )\right)-v_t^2\tau =0\\ \frac{v_t}{v_0}\left(\frac{v_t}{v_0}+\sin \theta \right)\left(1-\exp (-\tau )\right)-\frac{v_t^2}{v_0^2}\tau =0\end{array}}$

Representamos la variación de energía potencial, la variación de energía cinética y el trabajo de la fuerza de rozamiento en unidades de la energía inicial de la partícula

th=pi/6; %ángulo de tiro
k=980/60; %cociente vt/v0
hold on
f=@(t) k*(k+sin(th))*(1-exp(-t))-k^2*t;
tf=fzero(f,2*sin(th)/k); %tiempo de vuelo adimensional
fP=@(t) 2*(k*(k+sin(th))*(1-exp(-t))-k^2*t);
fK=@(t) (1+k^2+2*k*sin(th))*exp(-2*t)+k^2-2*k*(k+sin(th))*exp(-t)-1;
fW=@(t) (1+k^2+2*k*sin(th))*exp(-2*t)-2*k^2*t-4*k*(k+sin(th))*exp(-t)
-1+3*k^2+2*k*sin(th);
fplot(fP, [0,tf]) %potencial
fplot(fK, [0,tf]) %cinética
fplot(fW, [0,tf]) %trabajo
hold off
xlabel('gt/v_t')
ylabel ('E/(mv_0^2/2)')
grid on
legend('E_p','E_k','W','location','best')
title('Trabajo y energías')

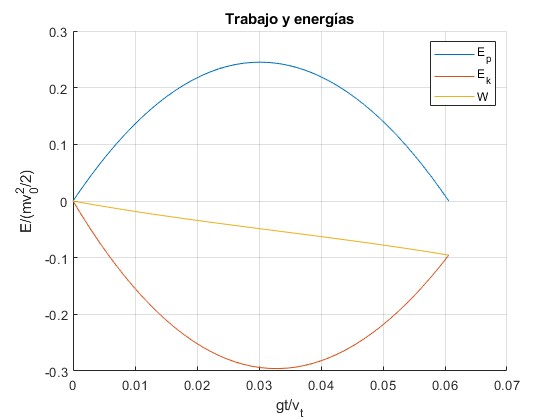
El proyectil sale del origen y llega al eje X, la variación de altura es cero, por tanto ΔE_p=0. El trabajo de la fuerza de rozamiento W es negativo. La energía cinética E_k disminuye al aumentar la altura del proyectil, se hace mínima cuando alcanza la altura máxima y luego, aumenta. La energía cinética final es menor que la inicial a causa del trabajo de la fuerza de rozamiento

Angulo de tiro óptimo

El ángulo de tiro óptimo es el que produce un alcance máximo. Cuando no hay rozamiento, el ángulo es 45°. Cuando hay rozamiento, como vemos en la gráfica anterior, es menor que 45°. En este apartado vamos a obtener el ángulo de tiro óptimo θ_m que produce el alcance máximo R_m

Partimos de la ecuación transcendente, a partir de la cual, calculamos el alcance R dado el ángulo de tiro θ

${\displaystyle \left(\frac{g}{b}+v_0\sin \theta \right)\frac{R}{v_0\cos \theta }+\frac{g}{b^2}\ln \left(1-\frac{Rb}{v_0\cos \theta }\right)=0}$

Expresamos de forma alternativa

${\displaystyle \begin{array}{l}\ln \left(1-\frac{Rb}{v_0\cos \theta }\right)=-\frac{b^2}{g}\left(\frac{g}{b}+v_0\sin \theta \right)\frac{R}{v_0\cos \theta }\\ R=\frac{v_0\cos \theta }{b}\left\{1-\exp \left(-\left(\frac{b}{v_0\cos \theta }+\frac{b^2}{g}\tan \theta \right)R\right)\right\}\end{array}}$

El alcance máximo R_m, se obtiene cuando dR/dθ=0

${\displaystyle \begin{array}{l}0=-\frac{v_0\sin {\theta }_m}{b}\left\{1-\exp \left(-\left(\frac{b}{v_0\cos {\theta }_m}+\frac{b^2}{g}\tan {\theta }_m\right)R_m\right)\right\}+\\ \frac{v_0\cos {\theta }_m}{b}\left\{\frac{b\sin {\theta }_m}{v_0{\cos }^2{\theta }_m}+\frac{b^2}{g}\frac{1}{{\cos }^2{\theta }_m}\right\}\exp \left(-\left(\frac{b}{v_0\cos {\theta }_m}+\frac{b^2}{g}\tan {\theta }_m\right)R_m\right)\\ -\frac{v_0\sin {\theta }_m}{b}\left\{\frac{b{R}_m}{v_0\cos {\theta }_m}\right\}+\frac{v_0\cos {\theta }_m}{b}\left\{\frac{b\sin {\theta }_m}{v_0{\cos }^2{\theta }_m}+\frac{b^2}{g}\frac{1}{{\cos }^2{\theta }_m}\right\}\left(1-\frac{b{R}_m}{v_0\cos {\theta }_m}\right)=0\end{array}}$

Simplificando

${\displaystyle R_m=\frac{v_0^2\cos {\theta }_m}{g\sin {\theta }_m+b{v}_0}}$

Introducimos el alcance R_m, en la ecuación transcendente que relaciona el alcance R y el ángulo de tiro θ

${\displaystyle \begin{array}{l}R=\frac{v_0\cos \theta }{b}\left\{1-\exp \left(-\left(\frac{b}{v_0\cos \theta }+\frac{b^2}{g}\tan \theta \right)R\right)\right\}\\ \frac{v_0^2\cos {\theta }_m}{g\sin {\theta }_m+b{v}_0}=\frac{v_0\cos {\theta }_m}{b}\left\{1-\exp \left(-\left(\frac{b}{v_0\cos {\theta }_m}+\frac{b^2}{g}\tan {\theta }_m\right)\frac{v_0^2\cos {\theta }_m}{g\sin {\theta }_m+b{v}_0}\right)\right\}\\ \frac{\sin {\theta }_m}{\sin {\theta }_m+\frac{b{v}_0}{g}}=\exp \left(-\frac{v_{0}b}{g}\frac{1+\frac{v_{0}b}{g}\sin {\theta }_m}{\sin {\theta }_m+\frac{v_{0}b}{g}}\right)\end{array}}$

Llamamos u=sinθ_m y c=v₀b/g

La ecuación transcendente que nos permite calcular el ángulo de tiro óptimo θ_m es

${\displaystyle \frac{u}{u+c}=\exp \left(-c\frac{1+cu}{u+c}\right)}$

Cuando c=1, la ecuación tiene una solución sencilla

${\displaystyle \frac{u}{u+1}=\frac{1}{e},\sin {\theta }_m=\frac{1}{e-1}}$

>> asind(1/(exp(1)-1))
ans =   35.5897

El ángulo de tiro óptimo es θ_m=35.6° para c=1

Cuando c≠1, vamos expresar el ángulo de tiro óptimo θ_m en función del parámetro c=v₀b/g. Teniendo en cuenta la propiedad de la función W de Lambert, W(z)exp(W(z))=z

${\displaystyle \begin{array}{l}\frac{u}{u+c}\exp \left(c\frac{1+cu}{u+c}\right)=1\\ \frac{u}{u+c}\exp \left(\frac{(u+c)+c^{2}u-u}{u+c}\right)=1\\ \frac{u}{u+c}e·\exp \left(\left(c^2-1\right)\frac{u}{u+c}\right)=1\\ \left(c^2-1\right)\frac{u}{u+c}\exp \left(\left(c^2-1\right)\frac{u}{u+c}\right)=\frac{c^2-1}{e}\{\begin{array}{l}z=\frac{c^2-1}{e}\\ W(z)=\left(c^2-1\right)\frac{u}{u+c}\end{array}\end{array}}$

Despejamos u=sinθ_m

${\displaystyle \begin{array}{l}u=\frac{cW(z)}{c^2-1-W(z)}\\ \sin {\theta }_m=\frac{cW\left(\frac{c^2-1}{e}\right)}{c^2-1-W\left(\frac{c^2-1}{e}\right)}\end{array}}$

Una vez que se ha calculado el ángulo de tiro óptimo θ_m, se determina el alcance máximo R_m

${\displaystyle R_m=\frac{v_0^2\cos {\theta }_m}{g\sin {\theta }_m+b{v}_0}}$

v0=60; %velocidad inicial
g=9.8; %aceleración de la gravedad
b=0.05; %rozamiento proporcional a la velocidad

c=v0*b/g;
lw=lambertw(0,(c^2-1)/exp(1));
ang=asin(c*lw/(c^2-1-lw));
Rm=v0^2*cos(ang)/(g*sin(ang)+b*v0);
fprintf('ángulo de tiro óptimo %2.1f, alcance máximo %3.1f\n',ang*180/pi,Rm)

ángulo de tiro óptimo 41.4, alcance máximo 285.0

Máximo de la trayectoria

En la posición del máximo, la componente vertical de la velocidad, v_y=dy/dt=0, despejamos el tiempo t y se introduce en la expresión de x e y

${\displaystyle \begin{array}{l}\exp \left(-bt\right)=\frac{1}{1+\frac{b{v}_{0y}}{g}},t=\frac{1}{b}\ln \left(1+\frac{b{v}_{0y}}{g}\right)\\ \{\begin{array}{l}{x}_m=\frac{v_0^2}{g}\frac{\sin \theta \cos \theta }{1+\frac{b{v}_0}{g}\sin \theta }\\ y_m=\frac{v_0}{b}\sin \theta -\frac{g}{b^2}\ln \left(1+\frac{b{v}_0}{g}\sin \theta \right)\end{array}\end{array}}$

Representamos las trayectorias de los proyectiles disparados con la misma velocidad v₀ para varios ángulos de tiro comprendidos entre 0 y 180°. Marcamos el máximo (x_m, y_m) de la trayectoria

v0=60; %velocidad inicial
g=9.8; %aceleración de la gravedad
b=0.01; %rozamiento proporcional a la velocidad
hold on
for ang=(15:15:175)*pi/180
    %trayectorias
    u=-1-b*v0*sin(ang)/g;
    T=(-u+lambertw(0,u*exp(u)))/b
    fplot(@(t) v0*cos(ang)*(1-exp(-b*t))/b, @(t) (g/b^2+v0*sin(ang)/b)
*(1-exp(-b*t))-g*t/b,[0,T]);
    %máximos
    xm=v0^2*sin(ang)*cos(ang)/(g+b*v0*sin(ang)); 
    ym=v0*sin(ang)/b-g*log(1+b*v0*sin(ang)/g)/b^2;
    plot(xm,ym,'ro','markersize',3,'markeredgecolor','r','markerfacecolor','r')
end
hold off
grid on
xlabel('x')
ylabel('y')
title('Máximos de la trayectoria')

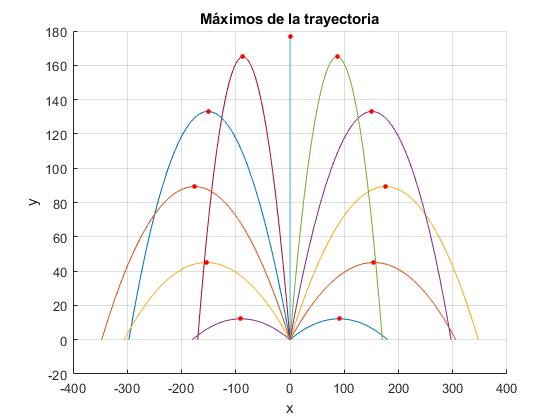
La forma explícita de la curva que une los puntos correspondientes al máximo de la trayectoria es muy complicada

Actividades

Se introduce:

• El valor del parámetro b en unidades s^-1, el control titulado Parámetro b
• La velocidad inicial v₀ en el control titulado Velocidad inicial.

Se pulsa el botón titulado Nuevo

El programa interactivo traza las trayectorias y calcula el alcance de los proyectiles disparados con ángulos de 10, 15, 20, 25, 30, 35, 40 y 45º (en color rojo)

Compara estas trayectorias con la que seguiría el mismo proyectil disparado con un ángulo de 45º en el vacío (en color azul).

En la parte superior derecha, se muestra el alcance R de cada uno de los proyectiles que se ha calculado resolviendo la ecuación trascendente en R. Observamos que el máximo alcance no se obtiene siempre para el ángulo de disparo de 45º.

Referencias

Apartado 'Angulo de tiro óptimo'

Seán M Stewart. On the trajectories of projectiles depicted in early ballistic woodcuts. Eur. J. Phys. 33 (2012) pp. 149-166