Para pequeños números Re<1, la fuerza de rozamiento sobre un cuerpo de forma esférica de radio R es

${\displaystyle F_r=6\pi \eta Rv}$

Que es la conocida fórmula de Stokes. La fuerza de rozamiento sobre una esfera que se mueve en régimen laminar en un medio es proporcional a la velocidad.

Para grandes números Re, el coeficiente de arrastre C_d es aproximadamente constante C_d≈ 0.4. La fuerza de rozamiento para una esfera de radio R vale

${\displaystyle F_r=0.2{\rho }_f\pi R^2{v}^2}$

La fuerza de rozamiento es proporcional al cuadrado de la velocidad.

Vamos a resolver el problema del lanzamiento de un cuerpo de forma esférica verticalmente hacia arriba con velocidad inicial v₀. Supondremos que el cuerpo tiene forma esférica de radio R, de masa m (o densidad del sólido ρ), y que se mueve en un medio de densidad ρ_f . Tomaremos como medida de la aceleración de la gravedad g=9.81 m/s²

Movimiento en el vacío.

La única fuerza que actúa es el peso. El movimiento del cuerpo es uniformemente acelerado.

${\displaystyle \begin{array}{l}v=v_0-gt\\ x=v_{0}t-\frac{1}{2}g{t}^2\end{array}}$

Fuerza de rozamiento proporcional a la velocidad

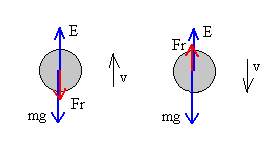
Sobre el cuerpo actúan tres fuerzas, el peso, el empuje y la fuerza de rozamiento.

La ecuación en su movimiento ascendente es

${\displaystyle m\frac{dv}{dt}={\rho }_f\frac{4}{3}\pi R^{3}g-\rho \frac{4}{3}\pi R^{3}g-6\pi \eta Rv}$

Escribimos esta ecuación de forma más sencilla

${\displaystyle \frac{dv}{dt}=-G-\alpha vG=\left(1-\frac{{\rho }_f}{\rho }\right)g\alpha =\frac{9\eta }{2R^2\rho }}$

Hemos denominado a G la aceleración efectiva de la gravedad

Integrando esta ecuación con la condición inicial de que en el instante t=0, la velocidad v=v₀.

${\displaystyle v=\left(v_0+\frac{G}{\alpha }\right)\exp \left(-\alpha t\right)-\frac{G}{\alpha }}$

Integrando nuevamente, obtenemos la posición del móvil (altura) en función del tiempo. En el instante inicial t=0, el cuerpo parte del origen x=0.

${\displaystyle x=\frac{G}{{\alpha }^2}\left(1+\frac{\alpha v_0}{G}\right)\left(1-\exp (-\alpha t)\right)-\frac{G}{\alpha }t}$

Cuando el cuerpo desciende no tenemos que volver a plantear la ecuación del movimiento ya que la velocidad cambia de signo.

Ejemplo

Un grano de arena de radio R=0.02 mm=0.00002 m se lanza verticalmente en el agua con una velocidad inicial de v₀=0.01 m/s.

Datos: densidad de la arena ρ=2670 kg/m³, densidad del agua ρ_f = 1000 kg/m³,  viscosidad η =0.001 kg/(m·s).

El valor de G=6.14 m/s² y el de α =4213 s^-1.

El número Re se mantiene inferior a 1, (en el instante inicial) por lo que se puede aplicar la fórmula de Stokes.

${\displaystyle \mathrm{Re}=\frac{{\rho }_{f}2·Rv}{\eta }=\frac{1000·2·0.02·{10}^{-3}·0.01}{0.001}=0.4}$

Comparamos el movimiento de una partícula lanzada verticalmente hacia arriba en el vacío con la velocidad inicial v₀=0.01 m/s y el movimiento vertical hacia arriba y hacia abajo del grano de arena en el agua.

Observamos cómo el grano de arena adquiere rápidamente una velocidad constante.

rho=1000; %densidad del agua
eta=0.001; %viscosidad
rho_s=2670; %densidad de la arena
r=0.02e-3; %%radio del grano de arena

alpha=9*eta/(2*r^2*rho_s);
G=(1-rho/rho_s)*9.8;

v0=0.01; %velocidad inicial
t=linspace(0,0.002,100);
v=v0-9.8*t; %vacío
vv=(v0+G/alpha)*exp(-alpha*t)-G/alpha; %agua
plot(t,v,t,vv);
legend('vacío','agua')
grid on
xlabel('t(s)')
ylabel('v(m/s)')
title('Movimiento vertical de una esfera')

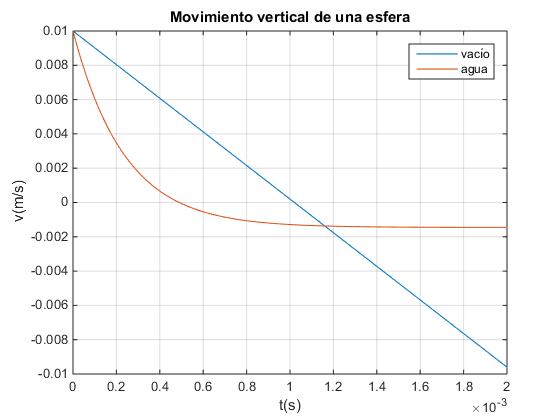
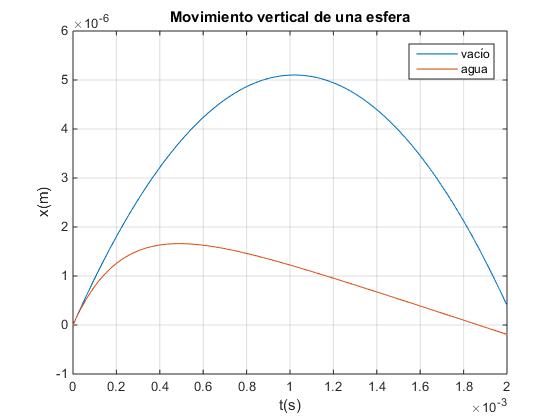
Creamos un script similar para comparar la posición del grano de arena en el agua y en el vacío, lanzando hacia arriba con la misma velocidad inicial v₀

rho=1000; %densidad del agua
eta=0.001; %viscosidad
rho_s=2670; %densidad de la arena
r=0.02e-3; %%radio del grano de arena

alpha=9*eta/(2*r^2*rho_s);
G=(1-rho/rho_s)*9.8;

v0=0.01; %velocidad inicial
t=linspace(0,0.002,100);
x=v0*t-9.8*t.^2/2;  %vacío
xx=(G/alpha^2)*(1+alpha*v0/G)*(1-exp(-alpha*t))-G*t/alpha; %agua
plot(t,x,t,xx);
legend('vacío','agua')
grid on
xlabel('t(s)')
ylabel('x(m)')
title('Movimiento vertical de una esfera')

Trabajo y energía

Se deja caer un cuerpo

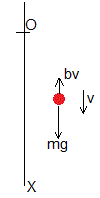
Se deja caer un cuerpo de masa m situado en el origen. La ecuación del movimiento, despreciando el empuje del fluido es

${\displaystyle m\frac{dv}{dt}=mg-bv}$

La velocidad límite constante se alcanza cuando la aceleración es nula, dv/dt=0, la fuerza de rozamiento bv se hace igual al peso, mg

${\displaystyle v_t=\frac{mg}{b}}$

Integrando obtenemos la velocidad v en función del tiempo

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{v}{\int }}\frac{dv}{g-\frac{b}{m}v}}={\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ -\frac{m}{b}\left\{\ln \left(g-\frac{b}{m}v\right)-\ln g\right\}=t\\ v=\frac{mg}{b}\left(1-\exp \left(-\frac{bt}{m}\right)\right)\\ v=v_t\left(1-\exp \left(-\frac{gt}{v_t}\right)\right)\end{array}}$

Integrando obtenemos la altura x en función del tiempo

${\displaystyle \begin{array}{l}v=\frac{dx}{dt}\\ {\displaystyle \underset{0}{\overset{x}{\int }}dx}=v_t{\displaystyle \underset{0}{\overset{t}{\int }}\left(1-\exp \left(-\frac{gt}{v_t}\right)\right)}dt\\ x=v_t\left(t+\frac{v_t}{g}\exp \left(-\frac{gt}{v_t}\right)\right)-\frac{v_t^2}{g}\end{array}}$

Trabajo y energías

• Variación de energía potencial

${\displaystyle \Delta E_p=-mgx=m{v}_t^2-mg{v}_t\left(t+\frac{v_t}{g}\exp \left(-\frac{gt}{v_t}\right)\right)}$

• Variación de energía cinética

${\displaystyle \Delta E_k=\frac{1}{2}m{v}^2=\frac{1}{2}m{v}_t^2{\left(1-\exp \left(-\frac{gt}{v_t}\right)\right)}^2}$

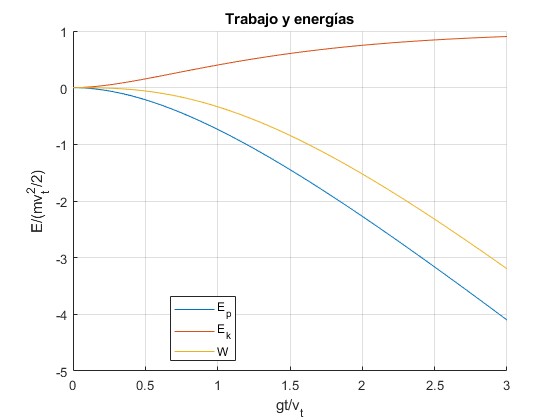
La energía cinética tiende hacia un valor constante

La suma es

${\displaystyle \begin{array}{l}\Delta E=\Delta E_k+\Delta E_p=\frac{3}{2}m{v}_t^2-mg{v}_{t}t-2m{v}_t^2\exp \left(-\frac{gt}{v_t}\right)+\frac{1}{2}m{v}_t^2\exp \left(-\frac{2gt}{v_t}\right)=\\ m{v}_t\left\{\frac{3}{2}{v}_t-gt-2v_t\exp \left(-\frac{gt}{v_t}\right)+\frac{v_t}{2}\exp \left(-\frac{2gt}{v_t}\right)\right\}\end{array}}$

• Trabajo de la fuerza de rozamiento

${\displaystyle \begin{array}{l}W=-{\displaystyle \underset{0}{\overset{x}{\int }}bvdx=}-{\displaystyle \underset{0}{\overset{t}{\int }}b{v}^{2}dt=-b{v}_t^2{\displaystyle \underset{0}{\overset{t}{\int }}{\left(1-\exp \left(-\frac{gt}{v_t}\right)\right)}^{2}dt}}=\\ -b{v}_t^2\left\{t+2\frac{v_t}{g}\exp \left(-\frac{gt}{v_t}\right)-\frac{v_t}{2g}\exp \left(-\frac{2gt}{v_t}\right)-\frac{3}{2}\frac{v_t}{g}\right\}=\\ m{v}_t\left\{\frac{3}{2}{v}_t-gt-2v_t\exp \left(-\frac{gt}{v_t}\right)+\frac{v_t}{2}\exp \left(-\frac{2gt}{v_t}\right)\right\}\end{array}}$

El trabajo de la fuerza de rozamiento es igual a la variación de energía (cinética más potencial)

Llamando $\tau =\frac{gt}{v_t}$, representamos el trabajo de la fuerza de rozamiento, la variación de energía cinética y la variación de energía potencial en unidades de la energía cinética final

${\displaystyle \begin{array}{l}\frac{W}{\frac{1}{2}m{v}_t^2}=3-2\tau -4e^{-\tau }+e^{-2\tau }\\ \frac{\Delta E_p}{\frac{1}{2}m{v}_t^2}=-2\left(\tau +e^{-\tau }-1\right)\\ \frac{\Delta E_k}{\frac{1}{2}m{v}_t^2}={\left(1-e^{-\tau }\right)}^2\end{array}}$

hold on
tf=3;
fplot(@(x) -2*(x+exp(-x)-1), [0,tf]) %potencial
fplot(@(x) (1-exp(-x)).^2, [0,tf]) %cinética
fplot(@(x) 3-2*x-4*exp(-x)+exp(-2*x), [0,tf]) %trabajo
hold off
xlabel('gt/v_t')
ylabel ('E/(mv_t^2/2)')
grid on
legend('E_p','E_k','W','location','best')
title('Trabajo y energías')

Se lanza hacia arriba

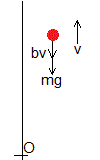
La partícula de masa m situada en el origen, se le proporciona una velocidad inicial v₀. La ecuación del movimiento, despreciando el empuje del fluido es

${\displaystyle m\frac{dv}{dt}=-mg-bv}$

Integrando obtenemos la velocidad v en función del tiempo

${\displaystyle \begin{array}{l}{\displaystyle \underset{v_0}{\overset{v}{\int }}\frac{dv}{g+\frac{b}{m}v}}=-{\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ \frac{m}{b}\left\{\ln \left(g+\frac{b}{m}v\right)-\ln \left(g+\frac{b}{m}{v}_0\right)\right\}=-t\\ v=\left(v_t+v_0\right)\exp \left(-\frac{gt}{v_t}\right)-v_t\end{array}}$

Integrando obtenemos la altura x en función del tiempo

${\displaystyle \begin{array}{l}v=\frac{dx}{dt}\\ {\displaystyle \underset{0}{\overset{x}{\int }}dx}={\displaystyle \underset{0}{\overset{t}{\int }}\left(\left(v_t+v_0\right)\exp \left(-\frac{gt}{v_t}\right)-v_t\right)}dt\\ x=\frac{v_t}{g}\left(v_t+v_0\right)\left(1-\exp \left(-\frac{gt}{v_t}\right)\right)-v_{t}t\end{array}}$

La partícula regresa al origen, cuando x=0, en el instante τ tal que

${\displaystyle \begin{array}{l}{v}_t\left(v_t+v_0\right)\left(1-\exp \left(-\frac{gt}{v_t}\right)\right)-v_{t}gt=0\\ \frac{v_t}{v_0}\left(1+\frac{v_t}{v_0}\right)\left(1-\exp \left(-\tau \right)\right)-\frac{v_t^2}{v_0^2}\tau =0\end{array}}$

Se resuelve la ecuación trascendente utilizando la función fzero de MATLAB

Trabajo y energías

• Variación de energía potencial

${\displaystyle \Delta E_p=mgx=m\left(v_t\left(v_t+v_0\right)\left(1-\exp \left(-\frac{gt}{v_t}\right)\right)-v_{t}gt\right)}$

• Variación de energía cinética

${\displaystyle \Delta E_k=\frac{1}{2}m{v}^2-\frac{1}{2}m{v}_0^2=\frac{1}{2}m{\left(\left(v_t+v_0\right)\exp \left(-\frac{gt}{v_t}\right)-v_t\right)}^2-\frac{1}{2}m{v}_0^2}$

La suma es

${\displaystyle \begin{array}{l}\Delta E=\Delta E_k+\Delta E_p=\\ m\left\{\frac{3}{2}{v}_t^2+v_0{v}_t-\frac{v_0^2}{2}-2v_t\left(v_t+v_0\right)\exp \left(-\frac{gt}{v_t}\right)+\frac{{\left(v_t+v_0\right)}^2}{2}\exp \left(-\frac{2gt}{v_t}\right)-v_{t}gt\right\}\end{array}}$

• Trabajo de la fuerza de rozamiento

${\displaystyle \begin{array}{l}W=-{\displaystyle \underset{0}{\overset{x}{\int }}bvdx=}-{\displaystyle \underset{0}{\overset{t}{\int }}b{v}^{2}dt=-b{\displaystyle \underset{0}{\overset{t}{\int }}{\left(\left(v_t+v_0\right)\exp \left(-\frac{gt}{v_t}\right)-v_t\right)}^{2}dt}}=\\ -b{v}_t\left\{-\frac{{\left(v_t+v_0\right)}^2}{2g}\exp \left(-\frac{2gt}{v_t}\right)+2\frac{v_t\left(v_t+v_0\right)}{g}\exp \left(-\frac{gt}{v_t}\right)+v_{t}t+\frac{{\left(v_t+v_0\right)}^2}{2g}-2\frac{v_t\left(v_t+v_0\right)}{g}\right\}=\\ m\left\{\frac{{\left(v_t+v_0\right)}^2}{2}\exp \left(-\frac{2gt}{v_t}\right)-2v_t\left(v_t+v_0\right)\exp \left(-\frac{gt}{v_t}\right)-v_{t}gt+\frac{3}{2}{v}_t^2-\frac{v_0^2}{2}+v_0{v}_t\right\}\end{array}}$

El trabajo de la fuerza de rozamiento es igual a la variación de energía (cinética más potencial)

Llamando $\tau =\frac{gt}{v_t}$, el trabajo de la fuerza de rozamiento, la variación de energía cinética y la variación de energía potencial en unidades de la energía cinética inicial

${\displaystyle \begin{array}{l}\frac{W}{\frac{1}{2}m{v}_0^2}={\left(\frac{v_t}{v_0}+1\right)}^2\exp \left(-2\tau \right)-4\frac{v_t}{v_0}\left(\frac{v_t}{v_0}+1\right)\exp \left(-\tau \right)-2\frac{v_t^2}{v_0^2}\tau +3\frac{v_t^2}{v_0^2}-1+2\frac{v_t}{v_0}\\ \frac{\Delta E_p}{\frac{1}{2}m{v}_0^2}=2\left\{\frac{v_t}{v_0}\left(\frac{v_t}{v_0}+1\right)\left(1-\exp \left(-\tau \right)\right)-\frac{v_t^2}{v_0^2}\tau \right\}\\ \frac{\Delta E_k}{\frac{1}{2}m{v}_0^2}={\left\{\left(\frac{v_t}{v_0}+1\right)\exp \left(-\tau \right)-\frac{v_t}{v_0}\right\}}^2-1\end{array}}$

Representamos estas magnitudes para b/m=0.01 s^-1, la velocidad inicial es v₀=60 m/s. v_t=mg/b=980 m/s, k=v_t/v₀=980/60

k=980/60; %cociente vt/v0
hold on
f=@(t) k*(k+1)*(1-exp(-t))-k^2*t;
tf=fzero(f,2/k); %tiempo de vuelo adimensional
fP=@(t) 2*(k*(k+1)*(1-exp(-t))-k^2*t);
fK=@(t) ((k+1)*exp(-t)-k).^2-1;
fW=@(t) (k+1)^2*exp(-2*t)-4*k*(k+1)*exp(-t)-2*k^2*t+3*k^2-1+2*k;
fplot(fP, [0,tf]) %potencial
fplot(fK, [0,tf]) %cinética
fplot(fW, [0,tf]) %trabajo
hold off
xlabel('gt/v_t')
ylabel ('E/(mv_0^2/2)')
grid on
legend('E_p','E_k','W','location','best')
title('Trabajo y energías')

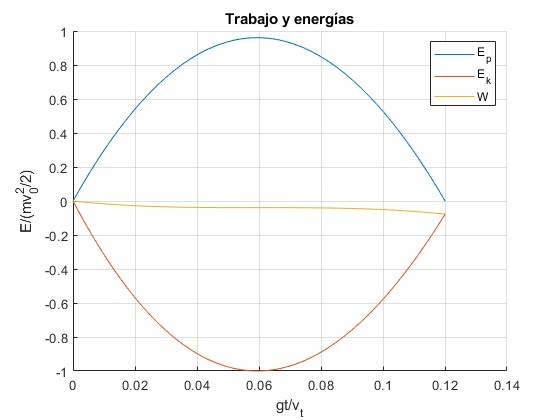
El proyectil sale del origen y retorna después de un tiempo de vuelo τ, la variación de altura es cero, por tanto ΔE_p=0. El trabajo de la fuerza de rozamiento W es negativo. La energía cinética E_k disminuye al aumentar la altura del proyectil, se hace mínima cuando alcanza la altura máxima y luego, aumenta. La energía cinética final es menor que la inicial debido al trabajo de la fuerza de rozamiento

Fuerza de rozamiento proporcional al cuadrado de la velocidad

Como la fuerza de rozamiento es proporcional al cuadrado de la velocidad, no cambia de signo cuando el cuerpo pasa de moverse hacia arriba a moverse hacia abajo. Por tanto, tenemos que plantear las ecuaciones del movimiento en dos etapas, cuando el cuerpo asciende y cuando el cuerpo desciende.

• Movimiento vertical hacia arriba

${\displaystyle m\frac{d{v}_{\uparrow }}{dt}={\rho }_f\frac{4}{3}\pi R^{3}g-\rho \frac{4}{3}\pi R^{3}g-0.2{\rho }_f\pi R^2{v}_{\uparrow }^2}$

Se puede escribir de una forma más simple

${\displaystyle \frac{d{v}_{\uparrow }}{dt}=-G\left(1+{\gamma }^2{v}_{\uparrow }^2\right)G=\left(1-\frac{{\rho }_f}{\rho }\right)g\gamma =\sqrt{0.15\frac{{\rho }_f}{\rho RG}}}$

Integrando esta ecuación con la condición inicial de que en el instante t=0, la velocidad v=v₀.

${\displaystyle \begin{array}{l}{\displaystyle \underset{v_0}{\overset{v_{\uparrow }}{\int }}\frac{d{v}_{\uparrow }}{1+{\gamma }^2{v}_{\uparrow }^2}}=-G{\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ {\frac{1}{\gamma }\arctan (\gamma v_{\uparrow })|}_{v_0}^{v_{\uparrow }}=-Gt\\ v_{\uparrow }=\frac{1}{\gamma }\tan \left(-\gamma Gt+\arctan (\gamma v_0)\right)\end{array}}$

Integrando nuevamente, obtenemos la posición del móvil (altura) en función del tiempo. En el instante inicial t=0, el cuerpo parte del origen x=0.

${\displaystyle \begin{array}{l}{x}_{\uparrow }={\displaystyle \underset{0}{\overset{t}{\int }}{v}_{\uparrow }dt}={\displaystyle \underset{0}{\overset{t}{\int }}\frac{1}{\gamma }}\tan \left(-\gamma Gt+\arctan \left(\gamma v_0\right)\right)dt\\ {\displaystyle \int \tan u·du=-\ln \left(\cos u\right)+C}\\ x_{\uparrow }={\frac{1}{{\gamma }^{2}G}\ln \left(\cos \left(-\gamma Gt+\arctan \left(\gamma v_0\right)\right)\right)|}_0^t=\\ x_{\uparrow }=\frac{1}{{\gamma }^{2}G}\ln \left(\cos \left(-\gamma Gt+\arctan \left(\gamma v_0\right)\right)\right)+\frac{1}{{\gamma }^{2}G}\ln \sqrt{1+{\left(\gamma v_0\right)}^2}\end{array}}$

Tiempo de ascenso y altura máxima alcanzada

${\displaystyle \begin{array}{l}{v}_{\uparrow }=0\\ t_{\uparrow }=\frac{1}{\gamma G}\arctan (\gamma v_0)\\ x_{máx}=\frac{1}{{\gamma }^{2}G}\ln \sqrt{1+{(\gamma v_0)}^2}\end{array}}$

• Movimiento vertical hacia abajo

La ecuación del movimiento es ahora

${\displaystyle \frac{d{v}_{\downarrow }}{dt}=-G\left(1-{\gamma }^2{v}_{\downarrow }^2\right)}$

Integrando esta ecuación con la condición inicial de que en el instante t=t_↑, la velocidad inicial v=0.

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{v_{\downarrow }}{\int }}\frac{d{v}_{\downarrow }}{1-{\gamma }^2{v}_{\downarrow }^2}}=-G{\displaystyle \underset{t_{\uparrow }}{\overset{t}{\int }}dt}\\ {\displaystyle \underset{0}{\overset{v_{\downarrow }}{\int }}\left(\frac{\frac{1}{2}}{1-\gamma v_{\downarrow }}+\frac{\frac{1}{2}}{1+\gamma v_{\downarrow }}\right)d{v}_{\downarrow }}=-G\left(t-t_{\uparrow }\right)\\ {\frac{1}{2\gamma }\ln \frac{1+\gamma v_{\downarrow }}{1-\gamma v_{\downarrow }}|}_0^{v_{\downarrow }}=-G\left(t-t_{\uparrow }\right)\\ \frac{1}{2\gamma }\ln \frac{1+\gamma v_{\downarrow }}{1-\gamma v_{\downarrow }}=-G\left(t-t_{\uparrow }\right)\\ v_{\downarrow }=-\frac{1}{\gamma }\tanh \left(\gamma G(t-t_{\uparrow })\right)\end{array}}$

donde t_↑ es el tiempo que tarda el cuerpo en ascender hasta la máxima altura v=0.

Integrando nuevamente, obtenemos la posición del móvil (altura) en función del tiempo. En el instante t=t_↑, el cuerpo parte de la altura máxima x_máx

${\displaystyle \begin{array}{l}{x}_{\downarrow }-x_{máx}={\displaystyle \underset{t_{\uparrow }}{\overset{t}{\int }}{v}_{\downarrow }dt}={\displaystyle \underset{t_{\uparrow }}{\overset{t}{\int }}-\frac{1}{\gamma }\tanh \left(\gamma G(t-t_{\uparrow })\right)dt=}\\ {\displaystyle \int \tanh u·du=\ln \cosh u+C}\\ x_{\downarrow }=x_{máx}-\frac{1}{{\gamma }^{2}G}\ln \left(\cosh \left(\gamma G(t-t_{\uparrow })\right)\right)=\\ \frac{1}{{\gamma }^{2}G}\ln \sqrt{1+{(\gamma v_0)}^2}-\frac{1}{{\gamma }^{2}G}\ln \left(\cosh \left(\gamma G(t-t_{\uparrow })\right)\right)=\frac{1}{{\gamma }^{2}G}\ln \frac{\sqrt{1+{(\gamma v_0)}^2}}{\cosh \left(\gamma G(t-t_{\uparrow })\right)}\end{array}}$

Tiempo de descenso

${\displaystyle \begin{array}{l}{x}_{\downarrow }=0\\ \cosh \left(\gamma G{t}_{\downarrow }\right)=\sqrt{1+{(\gamma v_0)}^2}\\ t_{\downarrow }=\frac{1}{\gamma G}\text{arccosh}\sqrt{1+{(\gamma v_0)}^2}=\frac{1}{\gamma G}\text{arcsinh}(\gamma v_0)=\\ \frac{1}{\gamma G}\ln \left(\gamma v_0+\sqrt{1+{(\gamma v_0)}^2}\right)\end{array}}$

Para llegar a estas relaciones se ha tenido en cuenta que

${\displaystyle \begin{array}{l}{\cosh }^{2}x-{\sinh }^{2}x=1\\ \sinh x=ux=\text{arcsinh}u\\ \frac{e^x-e^{-x}}{2}=u{e}^{2x}-2u{e}^x-1=0\\ e^x=u+\sqrt{u^2+1}x=\ln \left(u+\sqrt{u^2+1}\right)\end{array}}$

La suma del tiempo de ascenso t_↑ y el tiempo de descenso t_↓ es el tiempo de vuelo T.

T=t_↑+t_↓

El tiempo que tarda una partícula lanzada con velocidad v₀ en ascender y descender en ausencia de rozamiento es T=2v₀/g.

Ejemplo:

Consideremos una pelota de plástico que se lanza hacia arriba con una velocidad inicial v₀=5 m/s. Supongamos que su masa es de m=78.3 g y su radio de R=15 cm. Los datos de la densidad del aire es ρ_f =1.293 kg/m³ y su viscosidad es η=17.1 10^-6 kg/(m·s).

El valor de G=7.53 m/s² y el de γ =0.176 s/m. El número de Reynolds es en el momento del lanzamiento de la pelota vale

${\displaystyle \mathrm{Re}=\frac{1.293·2·0.15·5}{17.1·{10}^{-6}}=113421}$

El número Re está en el intervalo de validez de la fórmula de la fuerza de rozamiento, salvo cuando se aproxima a la máxima altura, la velocidad es próxima a cero. Ahora bien, en la mayor parte de la trayectoria la velocidad de la pelota es suficientemente alta para que se el número de Reynolds esté dentro del intervalo 1000<Re<200000.

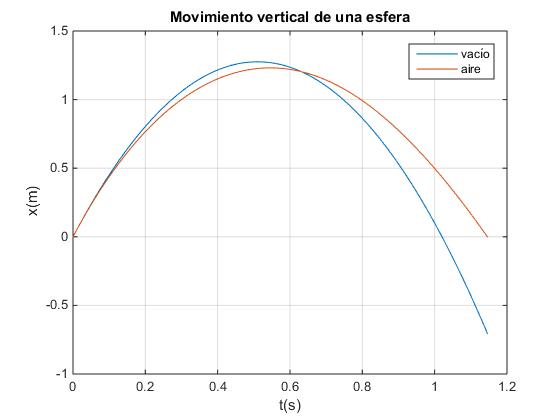
Comparamos el movimiento de una pelota lanzada verticalmente hacia arriba en el vacío con la velocidad inicial v₀=5 m/s , y el movimiento vertical hacia arriba y hacia abajo de la pelota en el aire .

rho=1.293; %densidad del aire
eta=17.1e-6; %viscosidad
masa=78.3e-3; %masa de la pelota
r=15e-2; %radio de la pelota
rho_s=masa/(4*pi*r^3/3); %densidad de la pelota

G=(1-rho/rho_s)*9.8;
gamma=sqrt(0.15*rho/(rho_s*r*G));

v0=5; %velocidad inicial
t_up=atan(gamma*v0)/(gamma*G);
t_down=log(gamma*v0+sqrt(1+(gamma*v0)^2))/(gamma*G);
t=linspace(0,t_up+t_down,100);
vv=(tan(-gamma*G*t+atan(gamma*v0))/gamma).*(t<t_up)
+(-tanh(gamma*G*(t-t_up))/gamma).*(t>t_up);
v=v0-9.8*t;  %vacío
plot(t,v, t,vv);
legend('vacío','aire')
grid on
xlabel('t(s)')
ylabel('v(m/s)')
title('Movimiento vertical de una esfera')

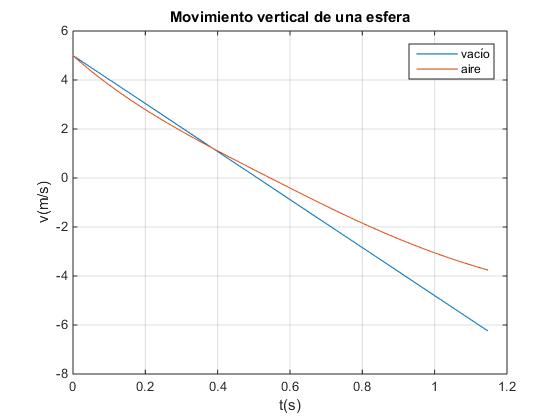
Creamos un script similar para comparar la posición de la pelota en el aire y en el vacío, lanzando hacia arriba con la misma velocidad inicial v₀

rho=1.293; %densidad del aire
eta=17.1e-6; %viscosidad
masa=78.3e-3; %masa de la pelota
r=15e-2; %radio de la pelota
rho_s=masa/(4*pi*r^3/3); %densidad de la pelota

G=(1-rho/rho_s)*9.8;
gamma=sqrt(0.15*rho/(rho_s*r*G));

v0=5; %velocidad inicial
t_up=atan(gamma*v0)/(gamma*G);
t_down=log(gamma*v0+sqrt(1+(gamma*v0)^2))/(gamma*G);
t=linspace(0,t_up+t_down,100);
xx=(log(sqrt(1.0+(gamma*v0)^2)*cos(-gamma*G*t+atan(gamma*v0)))
/(G*gamma^2)).*(t<t_up)
+(log(sqrt(1.0+(gamma*v0)^2)./cosh(gamma*G*(t-t_up)))
/(G*gamma^2)).*(t>t_up);           
x=v0*t-9.8*t.^2/2;  %vacío
plot(t,x, t,xx);
legend('vacío','aire')
grid on
xlabel('t(s)')
ylabel('x(m)')
title('Movimiento vertical de una esfera')

Actividades

En esta animación, vemos el movimiento de una esfera que es lanzada hacia arriba con velocidad v₀=5 m/s

• Se mueve en el aire que ejerce una fuerza de rozamiento proporcional al cuadrado de su velocidad (en color rojo)
• Se mueve en el vacío (en color azul)

Seleccionado Posición, se representa la altura de cada una de las esferas en función del tiempo. Seleccionado Velocidad, se representa la velocidad de cada una de las esferas en función del tiempo

Observamos que las representaciones gráficas coinciden con las trazadas mediante utilizando código MATLAB

Trabajo y energía

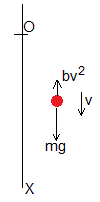
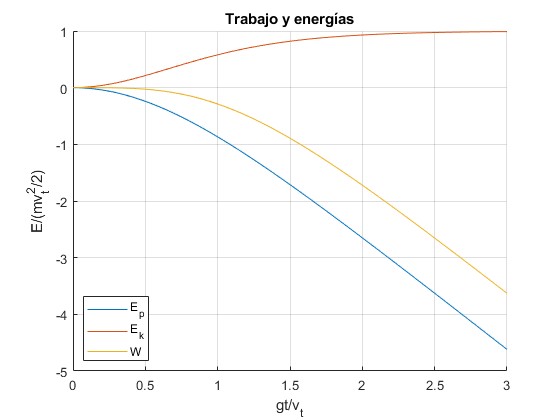
Se deja caer un cuerpo de masa m desde el origen, la ecuación del movimiento, despreciando el empuje del fluido es

${\displaystyle m\frac{dv}{dt}=mg-b{v}^2}$

La velocidad límite constante se alcanza cuando la aceleración es nula, dv/dt=0, la fuerza de rozamiento bv² se hace igual al peso, mg

${\displaystyle v_t=\sqrt{\frac{mg}{b}}}$

Integrando obtenemos la velocidad v en función del tiempo

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{v}{\int }}\frac{dv}{\frac{b}{m}{v}^2-g}}=-{\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ -\sqrt{\frac{m}{bg}}\text{arctanh}\left(\sqrt{\frac{b}{mg}}v\right)=-t\\ v=v_t\tanh \left(\frac{gt}{v_t}\right)\end{array}}$

Integrando obtenemos la altura x en función del tiempo

${\displaystyle \begin{array}{l}v=\frac{dx}{dt}\\ {\displaystyle \underset{0}{\overset{x}{\int }}dx}=v_t{\displaystyle \underset{0}{\overset{t}{\int }}\tanh \left(\frac{gt}{v_t}\right)dt}\\ x=\frac{v_t^2}{g}\ln \left(\cosh \left(\frac{gt}{v_t}\right)\right)\end{array}}$

Trabajo y energías

• Variación de energía potencial

${\displaystyle \Delta E_p=-mgx=-m{v}_t^2\ln \left(\cosh \left(\frac{gt}{v_t}\right)\right)}$

• Variación de energía cinética

${\displaystyle \Delta E_k=\frac{1}{2}m{v}^2=\frac{1}{2}m{v}_t^2{\tanh }^2\left(\frac{gt}{v_t}\right)}$

La energía cinética tiende hacia un valor constante

La suma es

${\displaystyle \Delta E=\Delta E_k+\Delta E_p=m{v}_t^2\left\{\frac{1}{2}{\tanh }^2\left(\frac{gt}{v_t}\right)-\ln \left(\cosh \left(\frac{gt}{v_t}\right)\right)\right\}}$

• Trabajo de la fuerza de rozamiento

${\displaystyle W=-{\displaystyle \underset{0}{\overset{x}{\int }}b{v}^{2}dx=}-{\displaystyle \underset{0}{\overset{t}{\int }}b{v}^{3}dt=-b{v}_t^3{\displaystyle \underset{0}{\overset{t}{\int }}{\tanh }^3\left(\frac{gt}{v_t}\right)dt}}}$

Teniendo en cuenta el resultado de la integral

${\displaystyle \begin{array}{l}{\displaystyle \int {\tanh }^3\left(ax\right)dx}={\displaystyle \int \left(1-\frac{1}{{\cosh }^2\left(ax\right)}\right)\tanh \left(ax\right)dx}\\ ={\displaystyle \int \tanh \left(ax\right)dx}-{\displaystyle \int \frac{\sinh \left(ax\right)}{{\cosh }^3\left(ax\right)}dx=}\\ \frac{1}{a}\ln \left(\cosh \left(ax\right)\right)+\frac{1}{2a}\frac{1}{{\cosh }^2\left(ax\right)}+C\\ \frac{1}{a}\ln \left(\cosh \left(ax\right)\right)-\frac{1}{2a}{\tanh }^2\left(ax\right)+C\text{'}\end{array}}$

El trabajo es

${\displaystyle \begin{array}{l}W=-b{v}_t^3\left\{\frac{v_t}{g}\ln \left(\cosh \left(\frac{g}{v_t}t\right)\right)-\frac{v_t}{2g}{\tanh }^2\left(\frac{g}{v_t}t\right)\right\}=\\ b\frac{v_t^4}{g}\left\{-\ln \left(\cosh \left(\frac{g}{v_t}t\right)\right)+\frac{1}{2}{\tanh }^2\left(\frac{g}{v_t}t\right)\right\}=\\ m{v}_t^2\left\{\frac{1}{2}{\tanh }^2\left(\frac{g}{v_t}t\right)-\ln \left(\cosh \left(\frac{g}{v_t}t\right)\right)\right\}\end{array}}$

El trabajo de la fuerza de rozamiento es igual a la variación de energía (cinética más potencial)

Llamando $\tau =\frac{gt}{v_t}$, representamos el trabajo de la fuerza de rozamiento, la variación de energía cinética y la variación de energía potencial en unidades de la energía cinética final

${\displaystyle \begin{array}{l}\frac{W}{\frac{1}{2}m{v}_t^2}={\tanh }^2\tau -\ln \left(\cosh \tau \right)\\ \frac{\Delta E_p}{\frac{1}{2}m{v}_t^2}=-2\ln \left(\cosh \tau \right)\\ \frac{\Delta E_k}{\frac{1}{2}m{v}_t^2}={\tanh }^2\tau \end{array}}$

hold on
tf=3;
fplot(@(x) -2*log(cosh(x)), [0,tf]) %potencial
fplot(@(x) 2*tanh(x).^2/2, [0,tf]) %cinética
fplot(@(x) tanh(x).^2-2*log(cosh(x)),[0,tf]) %trabajo
hold off
xlabel('gt/v_t')
ylabel ('E/(mv_t^2/2)')
grid on
legend('E_p','E_k','W','location','best')
title('Trabajo y energías')

Movimiento de caída de esferas en el agua

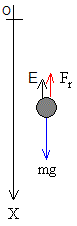
La densidad del agua es ρ_f=1 kg/m³. El coeficiente C_d≈ 0.5. La fuerza de rozamiento para una esfera de radio R en el agua vale

${\displaystyle F_r=0.25{\rho }_f\pi R^2{v}^2}$

La ecuación del movimiento es ma=mg-E-F_r. mg es el peso, E es el empuje y F_r es la fuerza de rozamiento en sentido contario de la velocidad v

${\displaystyle \begin{array}{l}m\frac{dv}{dt}=mg-E-F_r\\ m\frac{dv}{dt}=\rho \frac{4}{3}\pi R^{3}g-{\rho }_f\frac{4}{3}\pi R^{3}g-0.25{\rho }_f\pi R^2{v}^2\end{array}}$

Se puede escribir de una forma más simple,

${\displaystyle \frac{dv}{dt}=G(1-{\gamma }^2{v}^2)G=\left(1-\frac{{\rho }_f}{\rho }\right)g\gamma =\sqrt{0.1875\frac{{\rho }_f}{\rho RG}}}$

La velocidad límite v_T constante se alcanza cuando la aceleración es nula, dv/dt=0

${\displaystyle v_T^2=\frac{1}{{\gamma }^2}=\frac{1}{0.1875}R\left(\frac{\rho }{{\rho }_f}-1\right)g}$

Integrando esta ecuación con la condición inicial de que en el instante t=0, la velocidad inicial v=0.

${\displaystyle \begin{array}{l}\underset{0}{\overset{v}{{\displaystyle \int }}}\frac{dv}{1-{\gamma }^2{v}^2}=-G\underset{0}{\overset{t}{{\displaystyle \int }}}dt\\ \underset{0}{\overset{v}{{\displaystyle \int }}}\left(\frac{\frac{1}{2}}{1-\gamma v}+\frac{\frac{1}{2}}{1+\gamma v}\right)dv=-Gt\\ {\frac{1}{2\gamma }\ln \frac{1+\gamma v}{1-\gamma v}|}_0^v=-Gt\\ v=\frac{1}{\gamma }\tanh (\gamma Gt)\end{array}}$

Bolas de acero

Se dejan caer balas de acero de densidad ρ=7800 kg/m³ y de radios: 0.9, 2.0,8.2, 32.8 mm. Representamos la velocidad v de la bolas en función del tiempo t

k=7.8; %cociente densidad bola acero/densidad agua 
G=(1-1/k)*9.8;

hold on
disp('  radio (mm)    velocidad límite (m/s)') 
for R=[0.9,2.0,8.2,32.8]/1000
    gamma=sqrt(0.1875/(R*G*k));
    v=@(t) tanh(gamma*G*t)/gamma;
    fplot(v,[0,0.6],'displayName',num2str(R*1000))
    vT=sqrt(R*(k-1)*9.8/0.1875);
    disp([R*1000,vT])
end
hold off
grid on
legend('-DynamicLegend','location','northwest')
xlabel('t')
ylabel('v')
title('Bolas de acero')

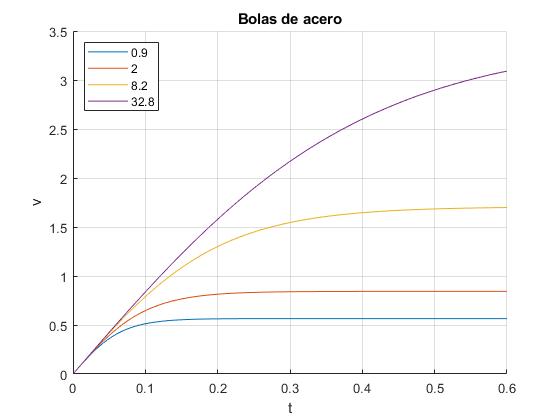
  radio (mm)  velocidad límite (m/s)
    0.9000    0.5656
    2.0000    0.8431
    8.2000    1.7072
   32.8000    3.4143

Bolas de plástico

Se dejan caer balas de plástico de densidad ρ=1200 kg/m³ y de radios: 1.1, 2.55, 10.2, 40.8 mm. Representamos la velocidad v de la bolas en función del tiempo t

k=1.2; %cociente densidad bola plástico/densidad agua 
G=(1-1/k)*9.8;

hold on
disp('  radio (mm)    velocidad límite (m/s)') 
for R=[1.1,2.55,10.2,40.8]/1000
    gamma=sqrt(0.1875/(R*G*k));
    v=@(t) tanh(gamma*G*t)/gamma;
    fplot(v,[0,0.6], 'displayName',num2str(R*1000))
    vT=sqrt(R*(k-1)*9.8/0.1875);
    disp([R*1000,vT])
end
hold off
grid on
legend('-DynamicLegend','location','northwest')
xlabel('t')
ylabel('v')
title('Bolas de plástico')

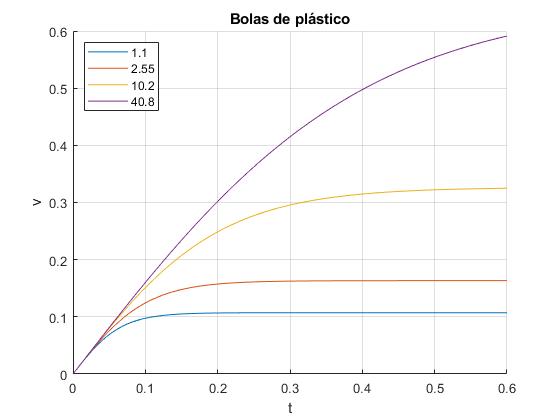
  radio (mm)  velocidad límite (m/s)
    1.1000    0.1072
    2.5500    0.1633
   10.2000    0.3265
   40.8000    0.6531

Movimiento de caída de esferas en el aire

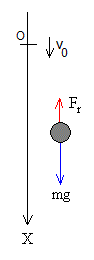
Al ser la densidad del aire ρ_f=1.225 kg/m³, pequeña, podemos despreciar el empuje frente al peso del cuerpo. La ecuación del movimiento de un cuerpo esférico de radio R y masa m es

${\displaystyle m\frac{dv}{dt}=mg-0.2{\rho }_f\pi R^2{v}^2}$

Se ha tomado la dirección positiva hacia abajo

A medida que el cuerpo cae, se incrementa la velocidad, la fuerza de rozamiento crece hasta que se iguala al peso. El cuerpo se mueve con velocidad constante denominada velocidad límite v_T

${\displaystyle v_T^2=\frac{mg}{0.2{\rho }_f\pi R^2}}$

La ecuación del movimiento se escribe

${\displaystyle \frac{dv}{dt}=g\left(1-\frac{v^2}{v_T^2}\right)}$

Integramos la ecuación diferencial con la condición inicial siguiente: en el instante t=0, la velocidad del cuerpo es v₀.

${\displaystyle \begin{array}{l}{\displaystyle \underset{v_0}{\overset{v}{\int }}\frac{dv}{1-v^2/v_T^2}}=g{\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ {\displaystyle \underset{v_0}{\overset{v}{\int }}\left(\frac{\frac{1}{2}}{1-v/v_T}+\frac{\frac{1}{2}}{1+v/v_T}\right)dv}=gt\\ {\frac{v_T}{2}\ln \frac{1+v/v_T}{1-v/v_T}|}_{v_0}^v=gt\\ \frac{1+v/v_T}{1-v/v_T}=\frac{1+v_0/v_T}{1-v_0/v_T}\exp (2gt/v_T)\\ \frac{1+v/v_T}{1-v/v_T}=\exp (2gt/v_T+2\alpha )\\ v=v_T\frac{\exp (gt/v_T+\alpha )-\exp (-gt/v_T-\alpha )}{\exp (gt/v_T+\alpha )+\exp (-gt/v_T-\alpha )}\\ v=v_T\tanh (gt/v_T+\alpha )\\ \exp (2\alpha )=\frac{1+v_0/v_T}{1-v_0/v_T}\\ \frac{v_0}{v_T}=\tanh \alpha \\ v=v_T\tanh \left(\left(\frac{gt}{v_T}\right)+{\tanh }^{-1}\left(\frac{v_0}{v_T}\right)\right)\end{array}}$

Integramos de nuevo para calcular la posición del cuerpo que cae en función del tiempo, sabiendo que en el instante t=0, parte del origen x=0.

${\displaystyle \begin{array}{l}x=\underset{0}{\overset{t}{{\displaystyle \int }}}v·dt=\underset{0}{\overset{t}{{\displaystyle \int }}}{v}_T\tanh \left(\frac{gt}{v_T}+{\tanh }^{-1}\left(\frac{v_0}{v_T}\right)\right)·dt\\ {{\displaystyle \int }}^{\text{}}\tanh u·du=\ln \cosh u+C\\ x=\frac{v_T^2}{g}\ln \frac{\cosh \left(\frac{gt}{v_T}+{\tanh }^{-1}\left(\frac{v_0}{v_T}\right)\right)}{\cosh \left({\tanh }^{-1}\left(\frac{v_0}{v_T}\right)\right)}\end{array}}$

Expresamos este resultado de forma más compacta

${\displaystyle \begin{array}{l}\frac{\cosh (u+\alpha )}{\cosh \alpha }=\frac{\exp (u+\alpha )-\exp (-u-\alpha )}{\exp (\alpha )-\exp (-\alpha )}=\frac{\exp (u)·\exp (2\alpha )-\exp (-u)+\exp (u)-\exp (-u)·\exp (-2\alpha )}{\exp (2\alpha )-\exp (-2\alpha )}=\\ =\frac{\exp (u)\frac{1+v_0/v_T}{1-v_0/v_T}-\exp (-u)+\exp (u)-\exp (-u)\frac{1-v_0/v_T}{1+v_0/v_T}}{\frac{1+v_0/v_T}{1-v_0/v_T}-\frac{1v_0/v_T}{1+v_0/v_T}}=\frac{\left(\exp (u)-\exp (-u)\right)+\frac{v_0}{v_T}\left(\exp (u)+\exp (-u)\right)}{2\frac{v_0}{v_T}}=\\ \frac{v_0}{v_T}\sinh (u)+\cosh (u)\end{array}}$

Obtenemos finalmente.

${\displaystyle x=\frac{v_T^2}{g}\ln \left(\frac{v_0}{v_T}\sinh \left(\frac{gt}{v_T}\right)+\cosh \left(\frac{gt}{v_T}\right)\right)}$

Aproximaciones

Desarrollo en serie de la función x(t)

${\displaystyle \begin{array}{l}x(t)\approx x(0)+{\frac{dx}{dt}|}_{t=0}t+\frac{1}{2!}{\frac{d^{2}x}{d{t}^2}|}_{t=0}{t}^2+\frac{1}{3!}{\frac{d^{3}x}{d{t}^3}|}_{t=0}{t}^3+\frac{1}{4!}{\frac{d^{4}x}{d{t}^4}|}_{t=0}{t}^4+\mathrm{...}\\ x=\frac{v_T^2}{g}\ln \left(\frac{v_0}{v_T}\sinh \left(\frac{gt}{v_T}\right)+\cosh \left(\frac{gt}{v_T}\right)\right)\\ \frac{dx}{dt}=\frac{v_T^2}{g}\frac{\frac{g{v}_0}{v_T^2}\cosh \left(\frac{gt}{v_T}\right)+\frac{g}{v_T}\sinh \left(\frac{gt}{v_T}\right)}{\frac{v_0}{v_T}\sinh \left(\frac{gt}{v_T}\right)+\cosh \left(\frac{gt}{v_T}\right)}=v_T\frac{\frac{v_0}{v_T}\cosh \left(\frac{gt}{v_T}\right)+\sinh \left(\frac{gt}{v_T}\right)}{\frac{v_0}{v_T}\sinh \left(\frac{gt}{v_T}\right)+\cosh \left(\frac{gt}{v_T}\right)}\\ \frac{d^{2}x}{d{t}^2}=\frac{g\left(1-\frac{v_0^2}{v_T^2}\right)}{{\left(\frac{v_0}{v_T}\sinh \left(\frac{gt}{v_T}\right)+\cosh \left(\frac{gt}{v_T}\right)\right)}^2}\\ \frac{d^{3}x}{d{t}^3}=-\frac{2g^2}{v_T}\left(1-\frac{v_0^2}{v_T^2}\right)\frac{\frac{v_0}{v_T}\cosh \left(\frac{gt}{v_T}\right)+\sinh \left(\frac{gt}{v_T}\right)}{{\left(\frac{v_0}{v_T}\sinh \left(\frac{gt}{v_T}\right)+\cosh \left(\frac{gt}{v_T}\right)\right)}^3}\\ \frac{d^{4}x}{d{t}^4}=-\frac{2g^3}{v_T^2}\left(1-\frac{v_0^2}{v_T^2}\right)\frac{1-2{\sinh }^2\left(\frac{gt}{v_T}\right)-4\frac{v_0}{v_T}\sinh \left(\frac{gt}{v_T}\right)\cosh \left(\frac{gt}{v_T}\right)-\frac{v_0^2}{v_T^2}\left(1+2{\cosh }^2\left(\frac{gt}{v_T}\right)\right)}{{\left(\frac{v_0}{v_T}\sinh \left(\frac{gt}{v_T}\right)+\cosh \left(\frac{gt}{v_T}\right)\right)}^4}\\ x(t)\approx v_{0}t+\frac{1}{2}g\left(1-\frac{v_0^2}{v_T^2}\right)t^2-\frac{g^2{v}_0}{3v_T^2}\left(1-\frac{v_0^2}{v_T^2}\right)t^3-\frac{g^3}{12v_T^2}\left(1+3\frac{v_0^4}{v_T^4}-4\frac{v_0^2}{v_T^2}\right)t^4+\mathrm{...}\end{array}}$

Cuando el cuerpo se deja caer, v₀=0, parte del reposo

${\displaystyle x(t)\approx \frac{1}{2}g{t}^2-\frac{g^3}{12v_T^2}{t}^4+\mathrm{...}}$

Utilizamos Math Symbolic de MATLAB para obtener estas aproximaciones

>> syms vT v0 g t;
>> v=vT*tanh(g*t/vT+atanh(v0/vT));
>> vv=taylor(x,t,0,'Order',3)
>> simplify(vv)
ans =(g^2*t^2*v0^3 - g^2*t^2*v0*vT^2 - g*t*v0^2*vT^2 + g*t*vT^4 + v0*vT^4)/vT^4

>> x=vT^2*log(v0*sinh(g*t/vT)/vT+cosh(g*t/vT))/g;
>>xx=taylor(x,t,0,'Order',3)
>> simplify(xx)
ans =(t*(2*g^2*t^2*v0^3 - 2*g^2*t^2*v0*vT^2 - 3*g*t*v0^2*vT^2 + 3*g*t*vT^4 + 
6*v0*vT^4))/(6*vT^4)

Utilizamos el comando latex en combinación con el programa MathType, para visualizar y arreglar el resultado

${\displaystyle \begin{array}{l}v\approx v_0+\left(1-\frac{v_0^2}{v_T^2}\right)gt+\left(\frac{v_0^2}{v_T^2}-1\right)\frac{v_0}{v_T^2}{g}^2{t}^2+\mathrm{...}\hfill \\ x\approx v_{0}t+\frac{g}{2}\left(1-\frac{v_0^2}{v_T^2}\right)t^2+\frac{1}{3}\frac{v_0}{v_T^2}\left(\frac{v_0^2}{v_T^2}-1\right)g^2{t}^3+\mathrm{...}\hfill \end{array}}$

Cuando el cuerpo parte del reposo, se hacen nulos varios términos del desarrollo en serie

Medida del coeficiente C_d

Supongamos un cuerpo de densidad ρ, de volumen V, sección trasversal A (perpendicular a la dirección del movimiento). La fuerza de rozamiento vale

${\displaystyle F_r=\frac{1}{2}{C}_d{\rho }_{f}A{v}^2}$

ρ_f es la densidad del medio y C_d se denomina coeficiente de arrastre, es una función del número de Reynolds, Re. Para grandes números Re, es aproximadamente constante

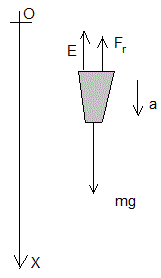
La ecuación del movimiento es ma=mg-E-F_r. mg es el peso, E es el empuje y F_r es la fuerza de rozamiento en sentido contario de la velocidad v

${\displaystyle \rho V\frac{dv}{dt}=\rho Vg-{\rho }_{f}Vg-\frac{1}{2}{C}_d{\rho }_{f}A{v}^2}$

Que escribimos de forma de forma alternativa

${\displaystyle \begin{array}{l}\frac{dv}{dt}=G\left(1-{\gamma }^2{v}^2\right)\\ G=g\left(1-\frac{{\rho }_f}{\rho }\right)\gamma =\sqrt{\frac{1}{2}\frac{{\rho }_f}{\rho }\frac{A}{V}\frac{C_d}{G}}\end{array}}$

Integramos la velocidad v respecto del tiempo t y a continuación, el desplazamiento x, sabiendo que en el instante inicial, t=0, x=0, v=0.

${\displaystyle \begin{array}{l}v=\frac{1}{\gamma }\tanh \left(\gamma Gt\right)\\ x=\frac{1}{{\gamma }^{2}G}\ln \left(\cosh (\gamma Gt)\right)\end{array}}$

Resultados que hemos obtenido en la sección 'Fuerza de rozamiento proporcional al cuadrado de la velocidad', tomando t_↑=0

Velocidad límite constante se obtiene cuando la aceleración es cero

${\displaystyle v_{\infty }=\frac{1}{\gamma }=\sqrt{2g\frac{V}{C_{d}A}\left(\frac{\rho }{{\rho }_f}-1\right)}}$

Midiendo la velocidad límite constante v_∞ obtenemos el coeficiente de arrastre C_d. En la práctica es complicado decidir cuando el cuerpo ha alcanzado aproximadamente esta velocidad. Una alternativa, consiste en medir el desplazamiento x del cuerpo durante un tiempo t.

Dado el desplazamiento x del cuerpo durante un tiempo t, resolvemos la ecuación trascendente

${\displaystyle x{\gamma }^{2}G=\ln \left(\cosh (\gamma Gt)\right)}$

Definimos las variables, z=γGt y k=xGγ²

${\displaystyle k{z}^2=\ln \left(\cosh (z)\right)}$

>> k=0.35;
>> f=@(z) k*z^2-log(cosh(z));
>> raiz=fzero(f,1)
 raiz =    1.7994   

Dado el valor de k obtenemos la raíz z, calculamos γ y despejamos el coeficiente de arrastre C_d

Referencias

Peter Timmerman, Jacobus P. van der Weele. On the rise and fall of a ball with linear or quadratic drag. Am. J. Phys. 67(6) June 1999, pp 538-546

Lindemuth J. The effect of air resistance on falling balls. Am. J. Phys. 39, July 1971, pp. 757-759

Ahmed Houari. Determining the drag coefficient of rotational symmetric objects falling through liquids. Eur. J. Phys. 33 (2012) 947-954.

Rod Cross. Terminal velocity of spheres in water. Phys. Educ. 55 (2020) 065003