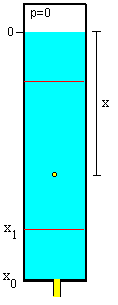
Se dispone de un tubo de vidrio parcialmente lleno de un fluido viscoso (aceite) de densidad ρ y viscosidad η. Por la parte superior, se conecta a una bomba de vacío, que reduce la presión a un valor pequeño p≈0. De modo, que la presión en el interior del fluido a una profundidad x es debida solamente a la altura de la columna de fluido ρgx.

Las burbujas de aire se inyectan por la parte inferior. El movimiento ascendente de las burbujas cuyo radio está comprendido entre 0.1 y 0.3 cm es suficientemente lento para que sigan una trayectoria rectilínea. Otras burbujas de radio mayor empiezan a oscilar a medida que ascienden, perdiendo su forma esférica a medida que se acercan a la superficie del líquido.

Transformación isotérmica

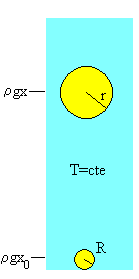
Consideremos una burbuja de forma esférica de radio r, que está a una profundidad x. La presión del aire en el interior de la burbuja es igual a la presión debida a la columna de fluido de altura x. La burbuja se expande isotérmicamente a medida que asciende. Si suponemos que el aire es un gas ideal de densidad ρ_a, tendremos que.

${\displaystyle {\rho }_{a}gx·\frac{4}{3}\pi r^3={\rho }_{a}g{x}_0·\frac{4}{3}\pi R^3,r=\sqrt[3]{\frac{x_0}{x}}R}$

Siendo R el radio de la burbuja a la profundidad x₀, cuando entra en el recipiente de vidrio.

Se desprecia la presión debido a la tensión superficial de la burbuja 2γ/r frente a la presión hidrostática. Para el agua, γ=72.8·10^-3 N/m.

Ecuación del movimiento

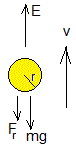
El peso de la burbuja, mg

La fuerza de empuje E. De acuerdo al principio de Arquímedes

${\displaystyle E=\rho g\frac{4}{3}\pi r^3}$

Supondremos que la velocidad de ascenso de la burbuja es suficientemente lenta para que el flujo sea laminar. La burbuja experimenta una fuerza de rozamiento F_r que se opone a su velocidad v. De acuerdo con la ley de Stokes

F_r=6πrη·v

La ecuación del movimiento es

${\displaystyle \begin{array}{l}m\frac{dv}{dt}=-mg+E-F_r,m={\rho }_a\frac{4}{3}\pi r^3\\ \frac{dv}{dt}=-g+\frac{\rho }{{\rho }_a}g-\frac{9\eta r}{2{\rho }_a{r}^3}v\end{array}}$

Integramos, suponiendo que la burbuja parte del reposo en el instante t=0

${\displaystyle {\displaystyle \underset{0}{\overset{v}{\int }}\frac{dv}{g\left(\frac{\rho }{{\rho }_a}-1\right)-\frac{9\eta }{2{\rho }_a{r}^2}v}}={\displaystyle \underset{0}{\overset{t}{\int }}dt}}$

Es una integral del tipo

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{x}{\int }}\frac{dx}{a-bx}=t}\\ -{\frac{1}{b}\ln \left(a-bx\right)|}_0^x=t\\ \ln \frac{a-bx}{a}=-bt\\ x=\frac{a}{b}\left(1-e^{-bt}\right)\end{array}}$

La velocidad de la burbuja de radio, supuesto constante, r es

${\displaystyle \begin{array}{l}v=\frac{g\left(\frac{\rho }{{\rho }_a}-1\right)}{\frac{9\eta r}{2{\rho }_a{r}^3}}\left(1-\exp \left(-\frac{9\eta }{2{\rho }_a{r}^2}t\right)\right)\\ v=\frac{2r^{2}g\left(\rho -{\rho }_a\right)}{9\eta }\left(1-\exp \left(-\frac{9\eta }{2{\rho }_a{r}^2}t\right)\right)\end{array}}$

Que tiende a una velocidad límite constante

${\displaystyle v_{\infty }=\frac{2r^2\left(\rho -{\rho }_a\right)g}{9\eta }\approx \frac{2r^2\rho g}{9\eta }}$

Con los datos

• Densidad del agua, ρ=1000 kg/m³
• Densidad del aire, ρ_a=1.2 kg/m³
• Viscosidad del agua, η=0.00105 kg/(m·s)
• El radio de la burbuja r=10^-3R, donde R es el radio de la burbuja en mm

${\displaystyle \exp \left(-\frac{9\eta }{2{\rho }_a{r}^2}t\right)=\exp \left(-\frac{9·0.00105}{2·1.2·{10}^{-6}{R}^2}t\right)=\exp \left(-3.94·{10}^3\frac{t}{R^2}\right)}$

En un tiempo muy pequeño, del orden de 10^-3 s la burbuja alcanza casi la velocidad límite constante

Deducción aproximada

La masa m y el peso mg de la burbuja de aire son despreciables. La segunda ley de Newton se escribe

E-F_r=ma≈0

${\displaystyle \rho g\frac{4}{3}\pi r^3+6\pi r\eta \frac{dx}{dt}=0}$

Cuando un cuerpo se mueve en el seno de un fluido viscoso en régimen laminar, al cabo de un cierto tiempo alcanza una velocidad límite constante, la resultante de las fuerzas que actúan sobre dicho cuerpo es cero.

Supondremos que la burbuja permanece en estado de equilibrio, el empuje y la fuerza de rozamiento son prácticamente iguales y de sentido contrario, la burbuja alcanza en cada momento la velocidad límite, aunque esta velocidad cambie con el tiempo.

Como el radio r de la burbuja es función de la profundidad x, la ecuación del movimiento se escribe en forma diferencial

${\displaystyle \frac{dx}{dt}+\frac{2}{9}\frac{\rho g}{\eta }{\left(\frac{x_0}{x}\right)}^{2/3}{R}^2=0}$

Separando variables e integrando, con la condición de que se empieza a contar el tiempo t=0 en el instante en el que la burbuja pasa por la marca situada a una profundidad x₁.

${\displaystyle \begin{array}{l}{\displaystyle \underset{x_1}{\overset{x}{\int }}{x}^{2/3}dx}=-\frac{2\rho g{x}_0^{2/3}{R}^2}{9\eta }{\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ x^{5/3}=x_1^{5/3}-\frac{10}{27}\frac{\rho g}{\eta }{x}_0^{2/3}{R}^{2}t\end{array}}$

Ejemplo1:

• Densidad ρ=870 kg/m³
• Viscosidad η=1.18 Pa·s
• Supongamos que el radio de la burbuja en la posición x₀=0.25 m es R=0.0015 m

Calculamos el tiempo t que tarda la burbuja en desplazarse desde la posición x₁=0.2  hasta la posición x=0.05 m

${\displaystyle {0.05}^{5/3}={0.2}^{5/3}-\frac{10}{27}\frac{870·9.8}{1.18}{0.25}^{2/3}{0.0015}^{2}tt=25.8\text{s}}$

Ejemplo 2:

El programa interactivo no nos proporciona el valor del radio inicial R de la burbuja a la profundidad x₀=0.25 cm. Midiendo con un cronómetro el tiempo t que tarda la burbuja en desplazarse entre las posiciones x₁=0.2 y x=0.05 m, despejamos en esta ecuación el radio R.

• Densidad ρ=870 kg/m3
• Viscosidad η=1.18 Pa·s

El tiempo t medido es de 14.60 s calcular el radio inicial R de la burbuja.

${\displaystyle {0.05}^{5/3}={0.2}^{5/3}-\frac{10}{27}\frac{870·9.8}{1.18}{0.25}^{2/3}{R}^2·14.6R=0.2\text{cm}}$

Actividades

Se introduce

• La viscosidad η del fluido (aceite) en Pa·s, en el control titulado Viscosidad.

• La densidad ρ del fluido en kg/m³, en el control titulado Densidad

• El programa interactivo fija el radio R de la burbuja a la profundidad x₀=0.25 en un valor aleatorio comprendido entre 0.001 y 0.003 m.

Se pulsa el botón titulado Nuevo

En la parte derecha, observamos como la burbuja se expande a medida que asciende y las dos fuerzas que actúan sobre la burbuja:

• El empuje que se incrementa al aumentar el volumen

• La fuerza de rozamiento que se incrementa al aumentar el radio y la velocidad de la burbuja

Ambas fuerzas se equilibran, alcanzando en cada instante la velocidad límite, aunque ésta aumenta a medida que la burbuja asciende.

En la experiencia real, si la velocidad de la burbuja se hace grande el flujo laminar desaparece y empieza a oscilar a medida que asciende, siguiendo una trayectoria compleja.

Utilizamos los botones pausa || y paso a paso >| para medir el tiempo que tarda la burbuja en desplazarse entre las dos marcas rojas en el tubo

Referencias

Vermillon R. A look at some rising bubbles. Am. J. Phys. 43 (2) February 1975, pp. 177-179