La fuerza de rozamiento sobre un cuerpo que se mueve en el seno de un fluido viscoso depende del número de Reynolds

${\displaystyle \mathrm{Re}=\frac{D{\rho }_{f}v}{\eta }}$

Donde D=2r es el diámetro de la esfera, ρ_f es la densidad del fluido, η es la viscosidad y v es la velocidad relativa entre el cuerpo y el fluido.

Para pequeños números de Reynolds, la fuerza de rozamiento es proporcional a la velocidad y viene dada por la fórmula de Stokes

${\displaystyle F_r=6\pi r\eta v}$

Sin embargo, la fórmula de Stokes no produce buenos resultados en las experincias de medida de la viscosidad del fluido que se describen en esta página

Oscilaciones verticales de la esfera

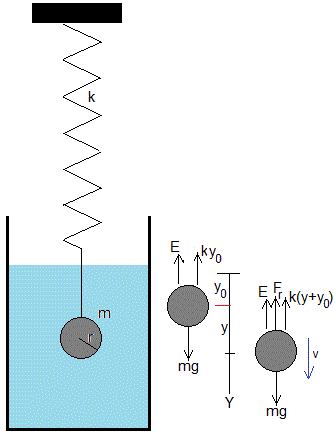
Una esfera de masa m, radio r y densidad ρ, m=ρ4πr³/3, está completamente sumergida en un fluido de densidad ρ_f y viscosidad η

La esfera cuega de una muelle elástico de constante k

Sitación de equilibrio

Las fuerza sobre la esfera son

• El peso, mg
• El empuje, ${\rho }_{f}g\frac{4}{3}\pi r^3$
• La fuerza que ejerce el muelle elástico deformado, ky₀

${\displaystyle k{y}_0=mg-{\rho }_{f}g\frac{4}{3}\pi r^3}$

Movimiento

Cuando la esfera se desplaza y de la posición de equilibrio y se mueve con velocidad v. Las fuerzas son

• El peso, mg
• El empuje, ${\rho }_{f}g\frac{4}{3}\pi r^3$
• La fuerza que ejerce el muelle elástico deformado, k(y+y₀)
• La fuerza de rozamiento F_r, de sentido contrario a la velocidad

La ecuación del movimiento es

${\displaystyle \begin{array}{l}m\frac{d^{2}y}{d{t}^2}=mg-{\rho }_{f}g\frac{4}{3}\pi r^3-F_r-k(y_0+y)\\ m\frac{d^{2}y}{d{t}^2}+F_r+ky=0\end{array}}$

Fórmula de Stokes

Para Re<1, la fuerza de rozamiento F_r=6πηrv

${\displaystyle \begin{array}{l}\frac{d^{2}y}{d{t}^2}+\frac{6\pi r\eta }{\rho \frac{4}{3}\pi r^3}\frac{dy}{dt}+\frac{k}{m}y=0\\ \frac{d^{2}y}{d{t}^2}+2\gamma \frac{dy}{dt}+{\omega }_0^{2}y=\mathrm{0,}\gamma =\frac{9\eta }{4\rho r^2},{\omega }_0^2=\frac{k}{m}\end{array}}$

La solución de esta ecuación diferencial para γ<ω₀

${\displaystyle y=A_0\exp \left(-\gamma t\right)\sin \left(\omega t+\phi \right),{\omega }^2={\omega }_0^2-{\gamma }^2}$

La constante A₀ y la fase φ se determinan a partir de las condiciones iniciales

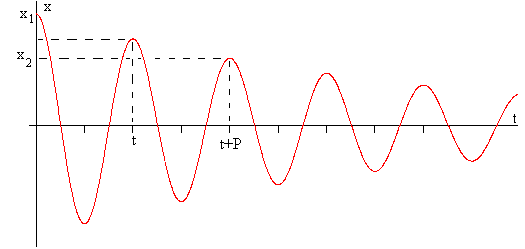
La amplitud, A₀exp(-γt) decrece exponencialmente con el tiempo. Se mide γ y obtenemos la viscosidad del fluido

${\displaystyle \gamma =\frac{9\eta }{4\rho r^2}}$

donde r es el radio de la esfera ρ su densidad y η la viscosidad del fluido. Los valores obtenidos de la viscosidad distan de los valores reales por lo que hemos de emplear otras aproximaciones

Fórmula de Landau–Lifshitz

La expresión general para la fuerza de rozamiento F_r sobre una esfera de radio r que oscila en un fluido de viscosidad η y densidad ρ_f es

${\displaystyle F_r=6\pi \eta r\left(1+\frac{r}{\delta }\right)v+3\pi r^2\left(1+\frac{2r}{9\delta }\right){\rho }_f\delta \frac{dv}{dt},\delta =\sqrt{\frac{2\eta }{{\rho }_f{\omega }_0}}}$

Obtenemos la fórmula de Stokes, F_r=6πηrv, si la esfera se mueve con velocidad constante y ω₀=0. Si el radio de la esfera r>>δ

${\displaystyle F_r\approx \frac{6\pi \eta r^2}{\delta }v+\frac{2\pi r^3}{3}{\rho }_f\frac{dv}{dt}}$

Que se aplica cuando las dimensiones del recipiente son grandes, para un recipiente cilíndrico de radio d, la fórmula aproximada es

${\displaystyle F_r\approx \left(\frac{6\pi \eta r^2}{\delta }v+\frac{2\pi r^3}{3}{\rho }_f\frac{dv}{dt}\right)\left(1+2.1\frac{r}{d}\right)}$

La ecuación diferencial del movimiento para esta expresión de la fuerza de rozamiento

${\displaystyle \begin{array}{l}m\frac{d^{2}y}{d{t}^2}+\left(\frac{6\pi \eta r^2}{\delta }\frac{dy}{dt}+\frac{2\pi r^3}{3}{\rho }_f\frac{d^{2}y}{d{t}^2}\right)\left(1+2.1\frac{r}{d}\right)+ky=0\\ \left(m+\frac{2\pi r^3}{3}{\rho }_f\left(1+2.1\frac{r}{d}\right)\right)\frac{d^{2}y}{d{t}^2}+\frac{6\pi \eta r^2}{\delta }\left(1+2.1\frac{r}{d}\right)\frac{dy}{dt}+ky=0\\ \frac{d^{2}y}{d{t}^2}+2\gamma \frac{dy}{dt}+{\omega }_0^{2}y=\mathrm{0,}\{\begin{array}{l}{m}_e=m+\frac{2\pi r^3}{3}{\rho }_f\left(1+2.1\frac{r}{d}\right)\\ \gamma =\frac{3\pi \eta r^2}{\delta m_e}\left(1+2.1\frac{r}{d}\right)\\ {\omega }_0^2=\frac{k}{m_e}\end{array}\end{array}}$

donde m_e es la masa efectiva

Si el recipiente es grande r<<d

${\displaystyle m_e\approx \rho \frac{4\pi r^3}{3}+{\rho }_f\frac{2\pi r^3}{3},r<<d}$

En la práctica real, ajustamos los datos experimentales (t_i, y_i), i=1,2,3... a la ecuación de las oscilaciones amortiguadas

${\displaystyle y=A_0\exp \left(-\gamma t\right)\sin \left(\omega t+\phi \right),\omega =\sqrt{{\omega }_0^2-{\gamma }^2}}$

calculando la constante de amortiguamiento γ, determinamos mediante la fórmula anterior, la viscosidad η.

Péndulo sumergido

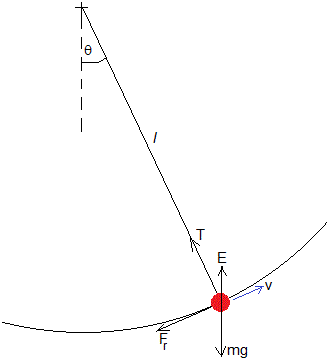
El péndulo consiste en una esfera de masa m, radio r y densidad ρ, m=ρ4πr³/3, unida a un hilo inextensible y de msas despreciable, de longitud l. La esfera está completamente sumergida en un fluido de densidad ρ_f y viscosidad η

Cuando la esfera se desplaza θ de la posición de equilibrio y se mueve con velocidad v. Las fuerzas son

• El peso, mg
• El empuje, ${\rho }_{f}g\frac{4}{3}\pi r^3$
• La tensión T del hilo
• La fuerza de rozamiento F_r, de sentido contrario a la velocidad

La ecuación del movimiento en la dirección tangencial es

${\displaystyle ml\frac{d^2\theta }{d{t}^2}=-\left(mg-{\rho }_{f}g\frac{4}{3}\pi r^3\right)\sin \theta -F_r}$

Cuando la amplitud es pequeña, θ≈sinθ

${\displaystyle ml\frac{d^2\theta }{d{t}^2}+F_r+\left(mg-{\rho }_{f}g\frac{4}{3}\pi r^3\right)\theta =0}$

Fórmula de Stokes

La fórmula de la fuerza de rozamiento es

${\displaystyle F_r\approx 6\pi \eta rv}$

La ecuación del movimiento se escribe

${\displaystyle \begin{array}{l}ml\frac{d^2\theta }{d{t}^2}+6\pi \eta rl\frac{d\theta }{dt}+\left(mg-{\rho }_{f}g\frac{4}{3}\pi r^3\right)\theta =0\\ \frac{d^2\theta }{d{t}^2}+2\gamma \frac{d\theta }{dt}+{\omega }_0^2\theta =\mathrm{0,}\{\begin{array}{l}\gamma =\frac{3\pi \eta r}{m}=\frac{9\eta }{4\rho r^2}\\ {\omega }_0^2=\frac{g}{l}\frac{m-{\rho }_f\frac{4}{3}\pi r^3}{m}\end{array}\end{array}}$

La expresión de la constante de amortiguamiento γ es la misma que en el primer apartado

Fórmula de Landau–Lifshitz

La fuerza de rozamiento, inluyendo el efecto del tamaño finito del recipiente (radio d), es

${\displaystyle F_r=\left(6\pi \eta r\left(1+\frac{r}{\delta }\right)l\frac{d\theta }{dt}+3\pi r^2\left(1+\frac{2r}{9\delta }\right){\rho }_f\delta l\frac{d^2\theta }{d{t}^2}\right)\left(1+2.1\frac{r}{d}\right),\delta =\sqrt{\frac{2\eta }{{\rho }_f{\omega }_0}}}$

La ecuación del movimiento

${\displaystyle \begin{array}{l}ml\frac{d^2\theta }{d{t}^2}+\left(6\pi \eta r\left(1+\frac{r}{\delta }\right)l\frac{d\theta }{dt}+3\pi r^2\left(1+\frac{2r}{9\delta }\right){\rho }_f\delta l\frac{d^2\theta }{d{t}^2}\right)\left(1+2.1\frac{r}{d}\right)+\left(mg-{\rho }_{f}g\frac{4}{3}\pi r^3\right)\theta =0\\ l\left(m+3\pi r^2\left(1+\frac{2r}{9\delta }\right){\rho }_f\delta \left(1+2.1\frac{r}{d}\right)\right)\frac{d^2\theta }{d{t}^2}+6\pi \eta r\left(1+\frac{r}{\delta }\right)\left(1+2.1\frac{r}{d}\right)l\frac{d\theta }{dt}+\left(mg-{\rho }_{f}g\frac{4}{3}\pi r^3\right)\theta =0\end{array}}$

que es la ecuación diferencial de las oscilaciones amortiguadas

${\displaystyle \frac{d^2\theta }{d{t}^2}+2\gamma \frac{d\theta }{dt}+{\omega }_0^2\theta =\mathrm{0,}\{\begin{array}{l}\gamma =\frac{3\pi \eta r\left(1+\frac{r}{\delta }\right)\left(1+2.1\frac{r}{d}\right)}{m+3\pi r^2\left(1+\frac{2r}{9\delta }\right){\rho }_f\delta \left(1+2.1\frac{r}{d}\right)}\\ {\omega }_0^2=\frac{mg-{\rho }_{f}g\frac{4}{3}\pi r^3}{l\left(m+3\pi r^2\left(1+\frac{2r}{9\delta }\right){\rho }_f\delta \left(1+2.1\frac{r}{d}\right)\right)}\end{array}}$

En la práctica real, ajustamos los datos experimentales (t_i, y_i), i=1,2,3... a la ecuación de las oscilaciones amortiguadas

${\displaystyle y=A_0\exp \left(-\gamma t\right)\sin \left(\omega t+\phi \right),\omega =\sqrt{{\omega }_0^2-{\gamma }^2}}$

calculando la constante de amortiguamiento γ, determinamos mediante la fórmula anterior, la viscosidad η.

Referencias

Sohaib Shamim, Wasif Zia, Muhammad Sabieh Anwar. Investigating viscous damping using a webcam.. Am. J. Phys. 7 (4), April 2010, pp. 433-436

José Costa Leme, Agostinho Oliveira. Pendulum Underwater – An Approach for Quantifying Viscosity. The Physics Teacher. Vol.55, December 2017. pp. 555-557