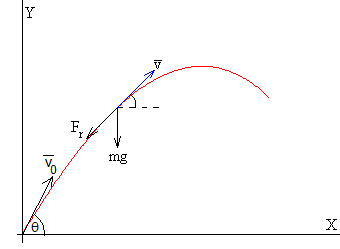
Un proyectil de masa m que se dispara desde el origen con velocidad v₀, haciendo un ángulo θ₀ con la horizontal

Si despreciamos el empuje, las fuerzas que actúan sobre el cuerpo de masa m son:

• El peso mg
• La fuerza de rozamiento F_r, que es de sentido contrario al vector velocidad (tangente a la trayectoria). ${\overrightarrow{F}}_r=-mbv\overrightarrow{·v}$

Las ecuaciones del movimiento del cuerpo serán por tanto.

${\displaystyle \begin{array}{l}\{\begin{array}{l}m\frac{d{v}_x}{dt}=-mb{v}_x\sqrt{v_x^2+v_y^2}\\ m\frac{d{v}_y}{dt}=-mg-mb{v}_y\sqrt{v_x^2+v_y^2}\end{array}\\ \{\begin{array}{l}\frac{d^{2}x}{d{t}^2}+b\frac{dx}{dt}\sqrt{{\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2}=0\\ \frac{d^{2}y}{d{t}^2}+b\frac{dy}{dt}\sqrt{{\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2}+g=0\end{array}\end{array}}$

Las condiciones iniciales son t=0, velocidad inicial: v_0x=v₀·cosθ, v_0y=v₀·sinθ, posición inicial: x=0, y=0.

Se resuelve este sistema de ecuaciones diferenciales mediante el procedimiento ode45 de MATLAB para mostrar las trayectorias del proyectil disparado con velocidad v₀=60 m/s para varios ángulo de tiro, θ=20, 40, 60, 80°.

function cuadrado_1
    b=0.0025; %parámetro
    v0=60;  %velocidad incial
    
    % x(1) es x, x(2) es dx/dt, x(3) es y, x(4) es dy/dt
    fg=@(t,x)[x(2);-b*sqrt(x(2)^2+x(4)^2)*x(2); x(4);
-9.8-b*sqrt(x(2)^2+x(4)^2)*x(4)];
    opts=odeset('events',@stop_proyectil);
    hold on
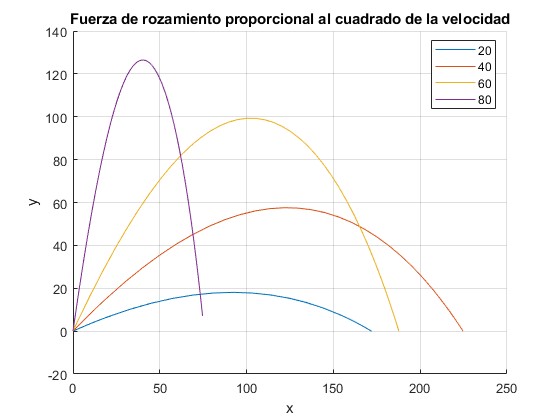
    for th_0=(20:20:80); %ángulo de tiro
        [~,x]=ode45(fg,[0,10],[0,v0*cosd(th_0),0,v0*sind(th_0)], opts);
        plot(x(:,1),x(:,3),'displayName',num2str(th_0)) %trayectoria
    end
    hold off
    grid on
    xlabel('x')
    legend('-DynamicLegend','location','best')
    ylabel('y')
    title('Fuerza de rozamiento proporcional al cuadrado de la velocidad')

    function [detect,stopin,direction]=stop_proyectil(t,x)
        detect=x(3); 
        stopin=1; 
        direction=-1; 
    end
end

Hemos definido una función stop_proyectil, para que se detenga el proceso de integración cuando el proyectil llega al suelo, ordenada y=0, en el código x(3)

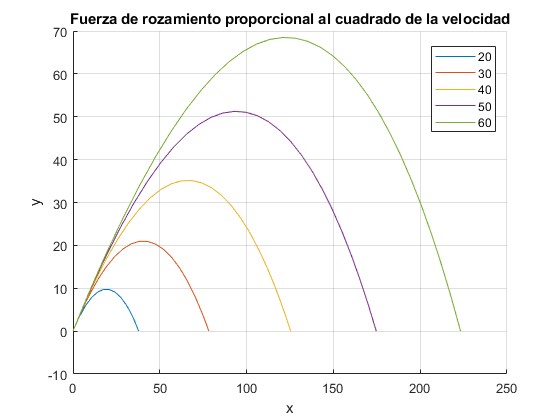
Mostramos las trayectorias de los proyectiles disparados con velocidad v₀=20,30, 40, 50, 60 m/s y con ángulo de tiro, θ=45°.

function cuadrado_2
    b=0.0025; %parámetro
    th_0=pi/4;  %ángulo de tiro (45)
    % x(1) es x, x(2) es dx/dt, x(3) es y, x(4) es dy/dt
    fg=@(t,x)[x(2);-b*sqrt(x(2)^2+x(4)^2)*x(2); x(4);
-9.8-b*sqrt(x(2)^2+x(4)^2)*x(4)];
    opts=odeset('events',@stop_proyectil_v2);
    hold on
    for v0=(20:10:60); %velocidad de disparo
        [~,x]=ode45(fg,[0,10],[0,v0*cos(th_0),0,v0*sin(th_0)], opts);
        plot(x(:,1),x(:,3),'displayName',num2str(v0)) %trayectoria
    end
    hold off
    grid on
    xlabel('x')
    legend('-DynamicLegend','location','best')
    ylabel('y')
    title('Fuerza de rozamiento proporcional al cuadrado de la velocidad')

    function [detect,stopin,direction]=stop_proyectil_v2(t,x)
        detect=x(3); 
        stopin=1; 
        direction=-1; 
    end
end

Actividades

Introducimos:

• El valor del parámetro b en unidades m^-1, en el control titulado b
• La velocidad inicial v₀ en el control titulado Velocidad inicial.

El programa interactivo traza y calcula el alcance de los proyectiles disparados con ángulos de 10, 15, 20, 25, 30, 35, 40 y 45º (en color rojo).

Compara estas trayectorias con la que seguiría el mismo proyectil disparado con un ángulo de 45º en el vacío (en color azul).

En la parte superior derecha, se muestra el alcance (aproximado) de cada uno de los proyectiles. Observamos que el máximo alcance del proyectil no se obtiene para el ángulo de disparo de 45º sino para un ángulo inferior. Y como cabía esperar, el alcance del proyectil disparado con 45º es inferior en un medio como el aire que en el vacío.

Experiencia

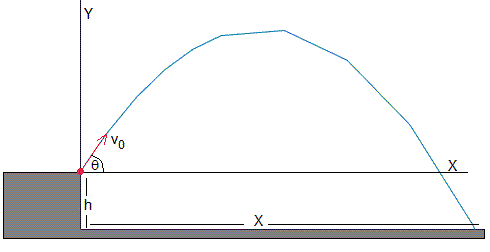
Se dispone de un dispositivo lanzador de proyectiles, por ejemplo el ME-6800 de PASCO que lanza bolas de acero de D=2.5 cm de diámetro con velocidades iniciales variables. Se pone el dispositivo sobre una mesa de h=1 m de altura, se ajusta el ángulo de tiro θ, se dispara y se mide el tiempo de vuelo T y el alcance horizontal X del proyectil.

Se compara las medidas con la del mismo proyectil describiendo una trayectoria parabólica con la misma velocidad inicial y en la misma dirección.

Datos:

• Densidad del aire, ρ_f=1.293 kg/m³ (0° C y 760 mm Hg de presión)
• Densidad del acero, ρ, de 7700 a 7900 kg/m³ (a 20° C)
• Viscosidad del aire, η=18.37·10^-6 kg/(m·s) (a 25° C)

Fuente: N.I. Koshkin , M. G. Shirkévich. Manual de física elemental. Editorial Mir (1975), págs, 36, 39 y 57

El número de Reynolds para un proyectil de forma esférica que se mueve a la velocidad v= 7 m/s es

${\displaystyle \mathrm{Re}=\frac{{\rho }_{f}Dv}{\eta }=\frac{1.293·0.025·7}{18.37·{10}^{-6}}=1.2318·{10}^4}$

Para números de Reynolds del orden de 10⁴ hasta 2·10⁵ el coeficiente de arrastre se mantiene casi constante y próximo a C_D=0.4

La expresión de la fuerza de rozamiento proporcional al cuadrado de la velocidad es

${\displaystyle F_r=C_D\frac{1}{2}{\rho }_{f}A{v}^2=0.4\frac{1}{2}1.293·\frac{\pi ·{0.025}^2}{4}{v}^2=1.2694·{10}^{-4}{v}^2}$

En el aparatado anterior, el módulo de fuerza de rozamiento se escribe F_r=mb·v². Donde m es la masa (producto de la densidad del acero por el volumen de la esfera). El parámetro b vale

${\displaystyle b=\frac{1.2694·{10}^{-4}}{7700\frac{1}{6}\pi {0.025}^3}=0.0020{\text{m}}^{\text{-1}}}$

El valor que se proporciona en el artículo de Pirooz Mohazzabi citado en las referencias es b=0.002141 m^-1

Dibujamos las trayectorias de los proyectiles disparados con velocidad v₀=10 m/s y con ángulos de tiro 0, 10, 20, ...90°.

function rozamiento
    b=0.002141; %parámetro
    v0=10;  %velocidad incial
    h=1; %altura 
    fg=@(t,x)[x(2);-b*sqrt(x(2)^2+x(4)^2)*x(2); x(4);
-9.8-b*sqrt(x(2)^2+x(4)^2)*x(4)];
    opts=odeset('events',@stop_proyectil_v2);
    hold on
    for th_0=(0:10:90)*pi/180 %ángulo de tiro
        [t,x]=ode45(fg,0:0.01:10,[0,v0*cos(th_0),0,v0*sin(th_0)], opts);
        plot(x(:,1),x(:,3)) %trayectoria
        disp([th_0*180/pi, t(end), x(end,1)])
    end
    grid on
    ylim([-1,5])
    xlabel('x(m)')
    ylabel('y(m)');
    title('Tiro con rozamiento')
    hold off

    function [detect,stopin,direction]=stop_proyectil_v2(~,x)
        detect=x(3)+h; 
        stopin=1; 
        direction=-1; 
    end
end

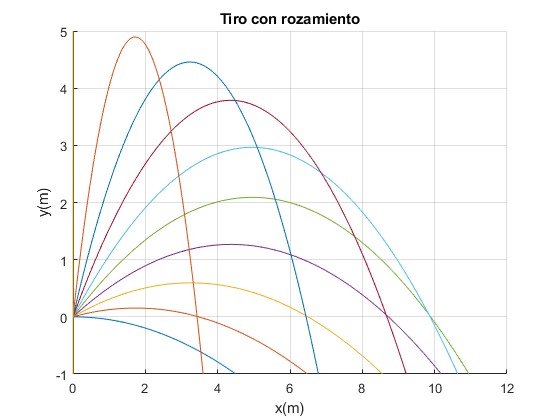
En esta tabla, la primera columna es el ángulo de tiro, la segunda, el tiempo de vuelo y la tercera, el alcance horizontal

         0    0.4525    4.5029
   10.0000    0.6629    6.4824
   20.0000    0.9192    8.5569
   30.0000    1.1893   10.1815
   40.0000    1.4479   10.9482
   50.0000    1.6782   10.6395
   60.0000    1.8682    9.2139
   70.0000    2.0097    6.7847
   80.0000    2.0969    3.5975
   90.0000    2.1263    0.0000

Actividades

Se introduce

• La velocidad inicial, v₀ entre 5 y 10 m/s, en el control titulado Velocidad inicial
• El ángulo de tiro, θ entre 0 y 90°, en el control titulado Angulo de tiro
• Se ha fijado el valor del parámetro b=0.002141 m^-1

Se resuelve por el procedimiento de Runge-Kutta, el sistema de dos ecuaciones diferenciales hasta que el proyectil choca con el suelo y=-h. Se traza la trayectoria del poyectil en color rojo.

Se traza la trayectoria parabólica (sin rozamiento) en color azul

${\displaystyle \{\begin{array}{l}{a}_x=0\\ a_y=-g\end{array}\{\begin{array}{l}{v}_x=v_0\cos \theta \\ v_y=v_0\sin \theta -gt\end{array}\{\begin{array}{l}x=v_0\cos \theta ·t\\ y=v_0\sin \theta ·t-\frac{1}{2}g{t}^2\end{array}}$

Cuando el proyectil llega al suelo y=-h, el tiempo de vuelo T y el alcance X son

${\displaystyle \begin{array}{l}T=\frac{v_0\sin \theta +\sqrt{v_0^2{\sin }^2\theta +2gh}}{g}\\ X=v_0\cos \theta ·T\end{array}}$

Soluciones analíticas aproximadas

Las ecuaciones del movimiento del cuerpo son:

${\displaystyle \begin{array}{l}\frac{d{v}_x}{dt}=-bv·v_x\\ \frac{d{v}_y}{dt}=-g-bv·v_y\\ v=\sqrt{v_x^2+v_y^2}\end{array}}$

Vamos a considerar tres casos:

• Para ángulos de tiro θ pequeños, v_x>>v_y, v=v_x. Se cumple en todos los puntos de la trayectoria

• Para ángulos de tiro θ grandes, próximos a 90°, |v_y|>>v_x, v=|v_y|. v_y es positivo en la rama ascendente, es negativo en la rama descendente y es nulo en el punto más alto de la trayectoria. Esta condición se cumple en la mayor parte de la trayectoria

• Para ángulos de tiro θ próximos a 45° se cumple que|v_y|≈v_x, $v=\sqrt{2}{v}_x=\sqrt{2}\left|v_y\right|$. Esta condición no se cumple en toda la trayectoria, así, v_y=0 en el punto más alto

En este apartado, vamos a obtener soluciones analíticas para estos tres casos

Angulos de tiro θ pequeños

Para ángulos de tiro θ pequeños, v_x>>v_y, v=v_x. Se cumple en todos los puntos de la trayectoria. Las ecuaciones del movimiento se escriben

${\displaystyle \begin{array}{l}\frac{d{v}_x}{dt}=-b{v}_x^2\\ \frac{d{v}_y}{dt}=-g-b{v}_x·v_y\end{array}}$

Integramos la primera ecuación diferencial, con la condición inicial de que en el instante t=0, v_x=v_0x=v₀·cosθ

${\displaystyle \begin{array}{l}{\displaystyle \underset{v_{0x}}{\overset{v_x}{\int }}\frac{d{v}_x}{v_x^2}=-{\displaystyle \underset{0}{\overset{t}{\int }}bdt}}\\ v_x=\frac{v_{0x}}{1+v_{0x}bt}\end{array}}$

Integramos la segunda ecuación diferencial, con la condición inicial de que en el instante t=0, v_y=v_0y=v₀·sinθ

${\displaystyle \frac{d{v}_y}{dt}+b\frac{v_{0x}}{1+v_{0x}bt}{v}_y=-g}$

Llamando z=v_y y a=b·v_0x. Escribimos la ecuación diferencial de la forma equivalente

${\displaystyle \frac{dz}{dt}+\frac{a}{1+at}z=-g}$

Probamos la solución z=u·v

${\displaystyle \begin{array}{l}\frac{du}{dt}v+\frac{dv}{dt}u+\frac{a}{1+at}u·v=-g\\ v\left(\frac{du}{dt}+\frac{a}{1+at}u\right)+\frac{dv}{dt}u=-g\end{array}}$

• Solución u. Igualamos el paréntesis a cero y obtenemos la expresión de u

${\displaystyle \begin{array}{l}\frac{du}{dt}+\frac{a}{1+at}u=0\\ \frac{du}{u}=-\frac{a}{1+at}dt\\ \ln u=-\ln (1+at)\\ u=\frac{1}{1+at}\end{array}}$

• Solución v

${\displaystyle \begin{array}{l}\frac{1}{1+at}\frac{dv}{dt}=-g\\ v=-g{\displaystyle \int \left(1+at\right)dt+C}\\ v=-\frac{g}{2a}{\left(1+at\right)}^2+C\end{array}}$

• Solución completa, z=u·v

${\displaystyle \begin{array}{l}z=uv=-\frac{1}{1+at}\left(\frac{g}{2a}{\left(1+at\right)}^2+C\right)\\ v_y=-\frac{g}{2b{v}_{0x}}\left(1+b{v}_{0x}t\right)-\frac{C}{1+b{v}_{0x}t}\end{array}}$

donde la constante C de integración de determina a partir de las condiciones iniciales, para t=0, v_y=v0y=v₀·sinθ

${\displaystyle v_y=\frac{v_{0y}-gt/2}{1+b{v}_{0x}t}-\frac{g}{2}t}$

>> syms z a t g v0y;
>> dsolve('Dz+a*z/(1+a*t)=-g','z(0)=v0y')
ans =v0y/(a*t + 1) - (g*t*(a*t + 2))/(2*(a*t + 1))
>> simplify(ans)
ans =-(a*g*t^2 + 2*g*t - 2*v0y)/(2*(a*t + 1))

Conocidas las componentes v_x=dx/dt y v_y=dy/dt de la velocidad en función del tiempo, integramos para obtener la posición x e y de la partícula en función del tiempo t, sabiendo que parte del origen en el instante t=0

• Abscisa x

${\displaystyle \begin{array}{l}x={\displaystyle \underset{0}{\overset{t}{\int }}\frac{v_{0x}}{1+v_{0x}bt}}dt\\ x=\frac{1}{b}\ln \left(1+v_{0x}bt\right)\end{array}}$

• Ordenada y

${\displaystyle \begin{array}{l}y={\displaystyle \underset{0}{\overset{t}{\int }}\left(\frac{v_{0y}-gt/2}{1+b{v}_{0x}t}-\frac{g}{2}t\right)}dt\\ y={\displaystyle \underset{0}{\overset{t}{\int }}\left(\frac{v_{0y}+\frac{g}{2b{v}_{0x}}}{1+b{v}_{0x}t}-\frac{g}{2b{v}_{0x}}-\frac{g}{2}t\right)}dt\\ y=\frac{1}{b{v}_{0x}}\left(v_{0y}+\frac{g}{2b{v}_{0x}}\right)\ln \left(1+b{v}_{0x}t\right)-\frac{g}{2b{v}_{0x}}t-\frac{g}{4}{t}^2\end{array}}$

Ecuación de la trayectoria. Despejamos el tiempo en la primera ecuación y sustituimos en la segunda

${\displaystyle \begin{array}{l}t=\frac{1}{b{v}_{0x}}\left(e^{bx}-1\right)\\ y=\left(v_{0y}+\frac{g}{2b{v}_{0x}}\right)\frac{x}{v_{0x}}-\frac{g}{4b^2{v}_{0x}^2}\left(e^{2bx}-1\right)\end{array}}$

El rango R, se obtiene cuando y=0.

${\displaystyle \begin{array}{l}\left(v_{0y}+\frac{g}{2b{v}_{0x}}\right)\frac{R}{v_{0x}}-\frac{g}{4b^2{v}_{0x}^2}\left(e^{2bR}-1\right)=0\\ e^{2bR}=2b\left(1+\frac{2b{v}_{0x}{v}_{0y}}{g}\right)R+1\end{array}}$

Expresamos el rango en términos de la función W de Lambert, solución de la ecuación trascendente a^b·x+c=d·x+f con a→e, b→2b, c→0, $d\to 2b\left(1+\frac{2b{v}_{0x}{v}_{0y}}{g}\right)$, f→1

${\displaystyle \begin{array}{l}R=-\frac{1}{2b}\left\{W\left(-\frac{1}{1+\beta }\exp \left(-\frac{1}{1+\beta }\right)\right)+\frac{1}{(1+\beta )}\right\}\\ \beta =\frac{2b{v}_{0x}{v}_{0y}}{g}\end{array}}$

Altura máxima, se obtiene dy/dx=0. La abscisa del máximo de y es

${\displaystyle \begin{array}{l}h=\left(v_{0y}+\frac{g}{2b{v}_{0x}}\right)\frac{1}{2b{v}_{0x}}\ln \left(\frac{2b{v}_{0x}{v}_{0y}}{g}+1\right)-\frac{v_{0y}}{2b{v}_{0x}}\\ h=\frac{v_{0y}}{2b{v}_{0x}}\left\{\left(\frac{\beta +1}{\beta }\right)\ln \left(\beta +1\right)-1\right\}\end{array}}$

Poniendo x=R, obtenemos el tiempo de vuelo

${\displaystyle \begin{array}{l}t=\frac{1}{b{v}_{0x}}\left(e^{bx}-1\right)\\ T=\frac{1}{b{v}_{0x}}\left\{\exp \left(-\frac{1}{2}\left\{W\left(-\frac{1}{1+\beta }\exp \left(-\frac{1}{1+\beta }\right)\right)+\frac{1}{(1+\beta )}\right\}\right)-1\right\}\end{array}}$

Lanzamos un proyectil con velocidad inicial v₀=9.8 m/s, con un ángulo de tiro θ=20°. Supondremos que el parámetro b=0.1 m^-1

b=0.1; %parámetro
v0=9.8;  %velocidad incial
angulo=20*pi/180; %ángulo de tiro
%solución analítica aproximada 
beta=2*b*v0*cos(angulo)*v0*sin(angulo)/9.8;
z=-exp(-1/(1+beta))/(1+beta);
R=-(lambertw(-1,z)+1/(1+beta))/(2*b); %alcance
f=@(x) (v0*sin(angulo)+9.8/(2*b*v0*cos(angulo)))*x/(v0*cos(angulo))-
9.8*(exp(2*b*x)-1)/(2*b*v0*cos(angulo))^2;

%procedimiento numérico
x0=[0,v0*cos(angulo),0,v0*sin(angulo)];
tspan=[0,2*v0*sin(angulo)/9.8]; %tiempo de vuelo sin rozamiento
%x(1) es x, x(2) es v_x, x(3) es y, x(4) es v_y
fg=@(t,x)[x(2);-b*sqrt(x(2)^2+x(4)^2)*x(2); x(4);-9.8-b*sqrt(x(2)^2+x(4)^2)*x(4)];
opts=odeset('events',@stop_proyectil_v2);
[t,x]=ode45(fg,tspan,x0,opts);

hold on
plot(x(:,1),x(:,3)) %trayectoria
fplot(f,[0,R])
grid on
legend('numérico','ángulo pequeño')
xlabel('x(m)')
ylabel('y(m)');
title('Tiro con rozamiento')
hold off

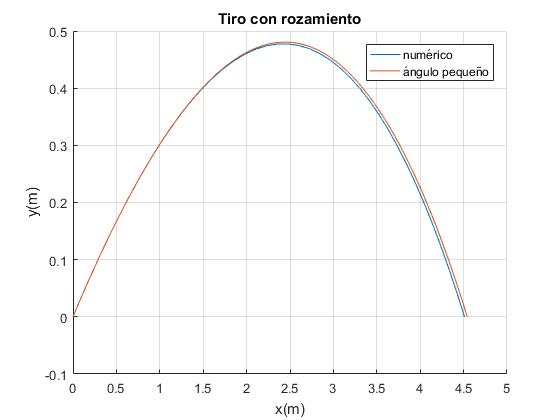
Comparamos la altura máxima h con el valor obtenido integrando las ecuaciones del movimiento por procedimientos numéricos, max(x(:,3)), el tiempo de vuelo T con t(end), y el rango R con x(end,1), tal como se aprecia en el código más abajo

>> h=v0*sin(angulo)*((beta+1)*log(beta+1)/beta-1)/(2*b*v0*cos(angulo))
h =    0.4806
>> max(x(:,3))
ans =    0.4773
>> T=(exp(-(lambertw(-1,z)+1/(1+beta))/2)-1)/(b*v0*cos(angulo))
T=    0.6246
>> t(end)
ans =    0.6228
>> R 
R =    4.5436
>> x(end,1)
ans =    4.5106

La solución numérica se aproxima a la solución analítica para ángulos pequeños de tiro

Angulos de tiro grandes, próximos a 90°

Para ángulos de tiro θ grandes, próximos a 90°, |v_y|>>v_x, v=|v_y|. v_y es positivo en la rama ascendente, es negativo en la rama descendente y es nulo en el punto más alto de la trayectoria. Las ecuaciones del movimiento se escriben

${\displaystyle \begin{array}{l}\frac{d{v}_x}{dt}=-mb\left|v_y\right|v_x\\ \frac{d{v}_y}{dt}=-g-b\left|v_y\right|v_y\end{array}}$

Debido a que v_y cambia de signo de la trayectoria ascendente a la descendente, hay que resolver este sistema de ecuaciones diferenciales en dos etapas

Trayectoria ascendente v_y>0

${\displaystyle \begin{array}{l}\frac{d{v}_x}{dt}=-b{v}_y{v}_x\\ \frac{d{v}_y}{dt}=-g-b{v}_y^2\end{array}}$

Integramos la segunda ecuación diferencial

${\displaystyle \begin{array}{l}{\displaystyle \underset{v_{0y}}{\overset{v_y}{\int }}\frac{d{v}_y}{g+b{v}_y^2}}=-{\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ \arctan \left(\sqrt{\frac{b}{g}}{v}_y\right)-\arctan \left(\sqrt{\frac{b}{g}}{v}_{0y}\right)=-\sqrt{bg}t\\ v_y=\sqrt{\frac{g}{b}}\tan \left(\phi -\sqrt{bg}t\right)\\ \phi =\arctan \left(\sqrt{\frac{b}{g}}{v}_{0y}\right)\end{array}}$

Conocido v_y, integramos la primera ecuación diferencial para obtener la expresión de v_x

${\displaystyle \begin{array}{l}{\displaystyle \underset{v_{0x}}{\overset{v_x}{\int }}\frac{d{v}_x}{v_x}}=-{\displaystyle \underset{0}{\overset{t}{\int }}b\sqrt{\frac{g}{b}}\tan \left(\phi -\sqrt{bg}t\right)dt}\\ \ln \frac{v_x}{v_{0x}}=-\ln \left(\frac{\cos \left(\phi -\sqrt{bg}t\right)}{\cos \phi }\right)\\ v_x=\frac{v_{0x}\cos \phi }{\cos \left(\phi -\sqrt{bg}t\right)}\end{array}}$

Conocidas las componentes v_x y v_y de la velocidad en función del tiempo, integramos para obtener la posición x, y, sabiendo que en el instante t=0, el proyectil parte del origen

• Abscisa x

${\displaystyle \begin{array}{l}\frac{dy}{dt}=\sqrt{\frac{g}{b}}\tan \left(\phi -\sqrt{bg}t\right)\\ y=\frac{1}{b}\ln \left(\frac{\cos \left(\phi -\sqrt{bg}t\right)}{\cos \phi }\right)\end{array}}$

• Ordenada y

${\displaystyle \begin{array}{l}\frac{dx}{dt}=\frac{v_{0x}\cos \phi }{\cos \left(\phi -\sqrt{bg}t\right)}\\ x=\frac{v_{0x}\cos \phi }{\sqrt{bg}}\ln \left(\frac{\tan \left(\phi /2+\pi /4\right)}{\tan \left(\phi /2-\sqrt{bg}t/2+\pi /4\right)}\right)\end{array}}$

Se ha utilizado el resultado de la integral de la inversa del coseno

Vértice de la trayectoria

Denominamos τ al tiempo que tarda la partícula en alcanzar la altura máxima, el vértice de la trayectoria

${\displaystyle \tau =\frac{\phi }{\sqrt{bg}}}$

Las coordenadas del vértice de la trayectoria son

${\displaystyle \begin{array}{l}{y}_1=-\frac{\ln \left(\cos \phi \right)}{b}\\ x_1=\frac{v_{0x}\cos \phi }{\sqrt{bg}}\ln \left(\tan \left(\frac{\pi }{4}+\frac{\phi }{2}\right)\right)\end{array}}$

Las componentes de velocidad v_1x y v_1y son

${\displaystyle \begin{array}{l}{v}_{1x}=v_{0x}\cos \phi \\ v_{1y}=0\end{array}}$

El vértice de la trayectoria es el punto de partida para la trayectoria descendente

Trayectoria descendente v_y<0

Las ecuaciones del movimiento se escriben

${\displaystyle \begin{array}{l}\frac{d{v}_x}{dt}=b{v}_y{v}_x\\ \frac{d{v}_y}{dt}=-g+b{v}_y^2\end{array}}$

Integramos la segunda ecuación diferencial

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{v_y}{\int }}\frac{d{v}_y}{-g+b{v}_y^2}}={\displaystyle \underset{\tau }{\overset{t}{\int }}dt}\\ -\frac{1}{\sqrt{gb}}{\displaystyle \underset{0}{\overset{u}{\int }}\frac{du}{1-u^2}}=(t-\tau )u=\sqrt{\frac{b}{g}}{v}_y\\ {\displaystyle \int \frac{du}{1-u^2}=\frac{1}{2}}\left\{{\displaystyle \int \frac{du}{1+u}+{\displaystyle \int \frac{du}{1-u}}}\right\}=\frac{1}{2}\ln \left(\frac{1+u}{1-u}\right)\\ -\frac{1}{2\sqrt{gb}}\ln \left(\frac{1+\sqrt{\frac{b}{g}}{v}_y}{1-\sqrt{\frac{b}{g}}{v}_y}\right)=(t-\tau )\\ v_y=\sqrt{\frac{g}{b}}\frac{\exp \left(-2\sqrt{gb}(t-\tau )\right)-1}{\exp \left(-2\sqrt{gb}(t-\tau )\right)+1}\end{array}}$

Conocida v_y, integramos la primera ecuación diferencial para obtener la expresión de v_x

${\displaystyle \begin{array}{l}{\displaystyle \underset{v_{1x}}{\overset{v_x}{\int }}\frac{d{v}_x}{v_x}}=b{\displaystyle \underset{\tau }{\overset{t}{\int }}\sqrt{\frac{g}{b}}\frac{\exp \left(-2\sqrt{gb}(t-\tau )\right)-1}{\exp \left(-2\sqrt{gb}(t-\tau )\right)+1}dt}\\ {\displaystyle \int \frac{e^{-2u}-1}{e^{-2u}+1}du=-{\displaystyle \int \tanh \left(u\right)}}·du=-\ln \left(\cosh \left(u\right)\right)\\ \ln \left(\frac{v_x}{v_{1x}}\right)=-\ln \left(\cosh \left(\sqrt{gb}(t-\tau )\right)\right)\\ v_x=\frac{v_{0x}\cos \phi }{\cosh \left(\sqrt{gb}(t-\tau )\right)}\end{array}}$

Conocidas las componentes v_x y v_y de la velocidad en función del tiempo, integramos para obtener las expresiones de x e y

• Abscisa x

${\displaystyle \begin{array}{l}\frac{dx}{dt}=\frac{v_{0x}\cos \phi }{\cosh \left(\sqrt{gb}(t-\tau )\right)}\\ {\displaystyle \int \frac{du}{\cosh u}}=2\arctan \left(e^u\right)\\ x-x_1=v_{0x}\cos \phi {\displaystyle \underset{\tau }{\overset{t}{\int }}\frac{dt}{\cosh \left(\sqrt{gb}(t-\tau )\right)}}\\ x=2\frac{v_{0x}\cos \phi }{\sqrt{gb}}\left\{\arctan \left(\exp \left(\sqrt{gb}(t-\tau )\right)\right)-\frac{\pi }{4}\right\}+\frac{v_{0x}\cos \phi }{\sqrt{bg}}\ln \left(\tan \left(\frac{\pi }{4}+\frac{\phi }{2}\right)\right)\end{array}}$

• Ordenada y

${\displaystyle \begin{array}{l}\frac{dy}{dt}=\sqrt{\frac{g}{b}}\frac{\exp \left(-2\sqrt{gb}(t-\tau )\right)-1}{\exp \left(-2\sqrt{gb}(t-\tau )\right)+1}\\ {\displaystyle \int \frac{e^{-2u}-1}{e^{-2u}+1}}du=-{\displaystyle \int \tanh (u)·du=-\ln \left(\cosh (u)\right)}\\ y-y_1=-\frac{1}{b}\ln \left(\cosh \left(\sqrt{gb}(t-\tau )\right)\right)\\ y=-\frac{1}{b}\ln \left(\cosh \left(\sqrt{gb}(t-\tau )\right)\cos \phi \right)\end{array}}$

Tiempo de vuelo, T que tarda en llegar al suelo, y=0

${\displaystyle \begin{array}{l}\cosh \left(\sqrt{gb}(t-\tau )\right)\cos \phi =1\\ \frac{e^u+e^{-u}}{2}=\frac{1}{\cos \phi }\\ e^{2u}-2\cos \phi e^u+1=0\\ T=\tau +\frac{1}{\sqrt{gb}}\ln \left(\frac{1}{\cos \phi }+\tan \phi \right)\end{array}}$

Introduciendo este tiempo T en la expresión de x obtenemos el rango R

Lanzamos un proyectil con velocidad inicial v₀=9.8 m/s, con un ángulo de tiro θ=70°. Supondremos que el parámetro b=0.1 m^-1

b=0.1; %parámetro
v0=9.8;  %velocidad incial
angulo=70*pi/180; %ángulo de tiro
%solución analítica aproximada 
phi=atan(sqrt(b/9.8)*v0*sin(angulo));
%coordendas del vértice de la trauyectoria
tau=phi/sqrt(9.8*b); %tiempo 
y1=-log(cos(phi))/b;
x1=v0*cos(angulo)*cos(phi)*log(tan(pi/4+phi/2))/sqrt(9.8*b);
f_X=@(t) v0*cos(angulo)*cos(phi)*log(tan(phi/2+pi/4)./
tan(phi/2+pi/4-sqrt(9.8*b)*t/2))/sqrt(9.8*b);
f_Y=@(t) log(cos(phi-sqrt(9.8*b)*t)/cos(phi))/b;
g_X=@(t) 2*v0*cos(angulo)*cos(phi)*
(atan(exp(sqrt(9.8*b)*(t-tau)))-pi/4)/sqrt(9.8*b)+x1;
g_Y=@(t) -log(cosh(sqrt(9.8*b)*(t-tau))*cos(phi))/b;
tFin=tau+log(1/cos(phi)+tan(phi))/sqrt(9.8*b); %tiempo total de vuelo

%procedimiento numérico
x0=[0,v0*cos(angulo),0,v0*sin(angulo)];
tspan=[0,2*v0*sin(angulo)/9.8]; %tiempo de vuelo sin rozamiento
fg=@(t,x)[x(2);-b*sqrt(x(2)^2+x(4)^2)*x(2); x(4);-9.8-b*sqrt(x(2)^2+x(4)^2)*x(4)];
opts=odeset('events',@stop_proyectil_v2);
[t,x]=ode45(fg,tspan,x0,opts);

hold on
plot(x(:,1),x(:,3)) %trayectoria
fplot(f_X,f_Y,[0,tau])
fplot(g_X,g_Y,[tau,tFin])
grid on
legend('numérico','ángulo grande')
xlabel('x(m)')
ylabel('y(m)');
title('Tiro con rozamiento')
hold off

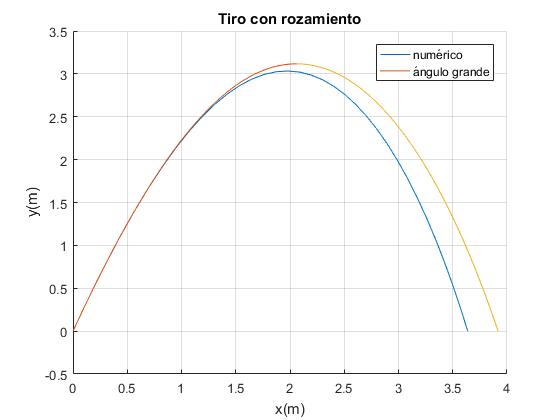
Comparamos la altura máxima y₁ con el valor obtenido integrando las ecuaciones del movimiento por procedimientos numéricos, max(x(:,3)), el tiempo de vuelo tFin con t(end), y el rango R con x(end,1), tal como se aprecia en el código más abajo

>> y1
y1 =    3.1173
>> max(x(:,3))
ans =    3.0336
>> tFin
tFin =    1.5965
>> t(end)
ans =    1.5732
>> R=2*v0*cos(angulo)*cos(phi)*(atan(exp(sqrt(9.8*b)*(T-tau)))-pi/4)/sqrt(9.8*b)+x1
R =    3.9180
>> x(end,1)
ans =    3.6386

Vemos que la solución numérica y la aproximación analítica para ángulos próximos a 90° se alejan bastante en comparación con el caso anterior, para ángulos de tiro pequeños

Angulos de tiro próximos a 45°

El módulo de la velocidad en la dirección horizontal es $v=\sqrt{2}{v}_x$, y en la dirección vertical $v=\sqrt{2}\left|v_y\right|$

Las ecuaciones del movimiento se escriben

${\displaystyle \begin{array}{l}\frac{d{v}_x}{dt}=-\sqrt{2}b{v}_x^2\\ \frac{d{v}_y}{dt}=-g-\sqrt{2}b\left|v_y\right|v_y\end{array}}$

Debido a que v_y cambia de signo de la trayectoria ascendente a la descendente, hay que resolver este sistema de ecuaciones diferenciales en dos etapas

Trayectoria ascendente v_y>0

${\displaystyle \begin{array}{l}\frac{d{v}_x}{dt}=-\sqrt{2}b{v}_x^2\\ \frac{d{v}_y}{dt}=-g-\sqrt{2}b{v}_y^2\end{array}}$

Trayectoria desscendente v_y<0

${\displaystyle \begin{array}{l}\frac{d{v}_x}{dt}=-\sqrt{2}b{v}_x^2\\ \frac{d{v}_y}{dt}=-g+\sqrt{2}b{v}_y^2\end{array}}$

La solución de la primera ecuación diferencial es la misma que hemos obtenido para ángulos de tiro pequeños, cambiando $b\to \sqrt{2}b$. La solución de la segunda ecuación diferencial es la misma que hemos obtenido para ángulos de tiro grandes, haciendo el mismo cambio

Lanzamos un proyectil con velocidad inicial v₀=9.8 m/s, con un ángulo de tiro θ=45°. Supondremos que el parámetro b=0.1 m^-1

b=0.1*sqrt(2); % (b=0.1), parámetro para la solución analítica
v0=9.8;  %velocidad incial
%solución analítica aproximada 
angulo=45*pi/180; %ángulo de tiro
phi=atan(sqrt(b/9.8)*v0*sin(angulo));
%coordendas del vértice de la trayectoria
tau=phi/sqrt(9.8*b); %tiempo 
y1=-log(cos(phi))/b;
x1=log(1+b*v0*cos(angulo)*tau)/b;
f_X=@(t) log(1+b*v0*cos(angulo)*t)/b;
f_Y=@(t) log(cos(phi-sqrt(9.8*b)*t)/cos(phi))/b;
g_X=@(t) log(1+b*v0*cos(angulo)*t)/b;
g_Y=@(t) -log(cosh(sqrt(9.8*b)*(t-tau))*cos(phi))/b;
tFin=tau+log(1/cos(phi)+tan(phi))/sqrt(9.8*b); %tiempo total de vuelo

%procedimiento numérico
b=0.1; %parámetro para la solución numérica
x0=[0,v0*cos(angulo),0,v0*sin(angulo)];
tspan=[0,2*v0*sin(angulo)/9.8]; %tiempo de vuelo sin rozamiento
fg=@(t,x)[x(2);-b*sqrt(x(2)^2+x(4)^2)*x(2); x(4);-9.8-b*sqrt(x(2)^2+x(4)^2)*x(4)];
opts=odeset('events',@stop_proyectil_v2);
[t,x]=ode45(fg,tspan,x0,opts);

hold on
plot(x(:,1),x(:,3)) %trayectoria
fplot(f_X,f_Y,[0,tau])
fplot(g_X,g_Y,[tau,tFin])
grid on
legend('numérico','ángulo medio')
xlabel('x(m)')
ylabel('y(m)');
title('Tiro con rozamiento')
hold off

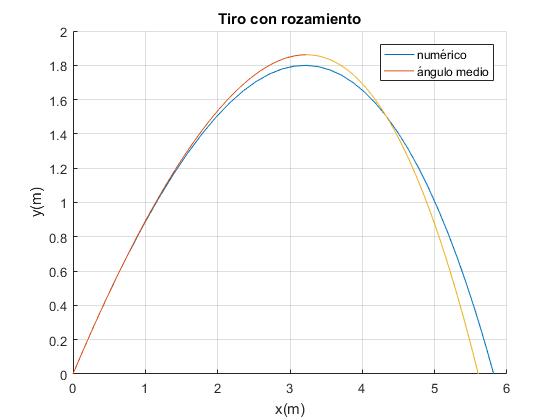
Comparamos la altura máxima y₁ con el valor obtenido integrando las ecuaciones del movimiento por procedimientos numéricos, max(x(:,3)), el tiempo de vuelo tFin con t(end), y el rango R con x(end,1), tal como se aprecia en el código más abajo

>> y1
y1 =    1.8614
>> max(x(:,3))
ans =    1.7997
>> tFin
tFin =    1.2334
>> t(end)
ans =    1.2078
>> R=log(1+b*v0*cos(angulo)*tFin)/b
R =    5.6032
>> x(end,1)
ans =    5.8162

Referencias

Al final de la siguiente página, titulada Fuerza de rozamiento proporcional al cuadrado de la velocidad (II)