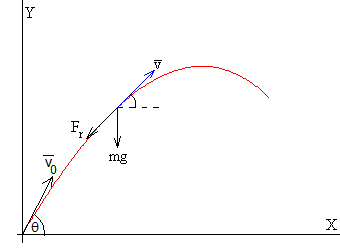
Un proyectil de masa m que se dispara desde el origen con velocidad v₀, haciendo un ángulo θ₀ con la horizontal

Si despreciamos el empuje, las fuerzas que actúan sobre el cuerpo de masa m son:

• El peso mg
• La fuerza de rozamiento constante F_r, que es de sentido contrario al vector velocidad (tangente a la trayectoria). ${\overrightarrow{F}}_r=-mb\frac{\overrightarrow{v}}{v}$

Las ecuaciones del movimiento del cuerpo serán por tanto.

${\displaystyle \begin{array}{l}m\frac{d{v}_x}{dt}=-mb\frac{v_x}{\sqrt{v_x^2+v_y^2}}\hfill \\ m\frac{d{v}_y}{dt}=-mg-mb\frac{v_y}{\sqrt{v_x^2+v_y^2}}\hfill \end{array}}$

Las condiciones iniciales son t=0, velocidad inicial: v_0x=v₀·cosθ₀, v_0y=v₀·sinθ₀, posición inicial: x=0, y=0.

Este sistema de ecuaciones diferenciales se resuelve aplicando procedimientos numéricos.

b=0.25*9.8; %parámetro
v0=50;  %velocidad incial

x0=zeros(1,4);
x0(1)=0;  % x
x0(3)=0; % y
tspan=[0,10];
fg=@(t,x)[x(2);-b*x(2)/sqrt(x(2)^2+x(4)^2); x(4);-9.8-b*x(4)/sqrt(x(2)^2+x(4)^2)];
opts=odeset('events',@stop_proyectil_v2);
hold on
for angulo=(10:5:45)*pi/180; %ángulo de tiro
    x0(2)=v0*cos(angulo); % vx
    x0(4)=v0*sin(angulo); % vy
    [t,x]=ode45(fg,tspan,x0,opts);
    plot(x(:,1),x(:,3)) %trayectoria
end
hold off
grid on
xlabel('x(m)')
ylabel('y(m)');
title('tiro con rozamiento')

Definimos una función para que se detenga el proceso de integración cuando el proyectil llega al suelo, ordenada y=0, en el código x(3)

function [detect,stopin,direction]=stop_proyectil_v2(t,x)
    detect=x(3); 
    stopin=1; 
    direction=-1; 
end

Actividades

Introducimos:

• El valor del parámetro b, en el control titulado b
• La velocidad inicial v₀ en el control titulado Velocidad inicial.

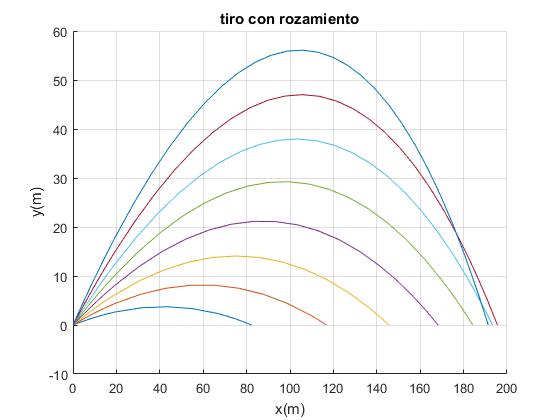
El programa interactivo traza y calcula el alcance de los proyectiles disparados con ángulos de 10, 15, 20, 25, 30, 35, 40 y 45º (en color rojo).

Compara estas trayectorias con la que seguiría el mismo proyectil disparado con un ángulo de 45º en el vacío (en color azul).

En la parte superior derecha, se muestra el alcance (aproximado) de cada uno de los proyectiles. Observamos que el máximo alcance del proyectil no se obtiene para el ángulo de disparo de 45º sino para un ángulo inferior. Y como cabía esperar, el alcance del proyectil disparado con 45º es inferior en un medio como el aire que en el vacío.

Solución analítica

Consideremos un proyectil de masa m, que es lanzado desde el origen O con velocidad v₀ haciendo un ángulo θ₀ con el eje X. En un momento dado, la posición del proyectil es (x,y), su vector velocidad v es tangente a la trayectoria y forma un ángulo θ con el eje X.

Las fuerzas que actúan sobre el proyectil son:

• el peso, mg
• la fuerza de rozamiento F_r=fg, tiene la dirección de la velocidad y de sentido contrario

La razón para escribir la fuerza de rozamiento como producto b=fg es la de mantener la misma notación que en la página titulada Proyectil que desliza sobre un plano inclinado

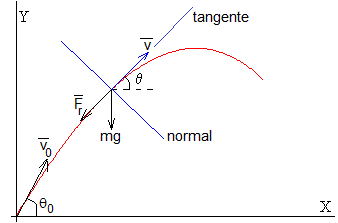
Escribimos las ecuaciones del movimiento en la dirección tangencial y en la dirección normal

${\displaystyle \begin{array}{l}m\frac{dv}{dt}=-mg\sin \theta -fg\\ m\frac{v^2}{\rho }=mg\cos \theta \end{array}}$

donde ρ es el radio de curvatura de la trayectoria.

En el intervalo de tiempo comprendido entre t y t+dt, la dirección del vector velocidad cambia un ángulo dθ, que es el ángulo entre las tangentes o entre las normales. El móvil se desplaza en este intervalo de tiempo un arco ds=ρ·dθ, tal como se aprecia en la figura.

${\displaystyle \frac{dv}{dt}=\frac{dv}{ds}\frac{ds}{dt}=v\frac{dv}{ds}=\frac{v}{\rho }\frac{dv}{d\theta }}$

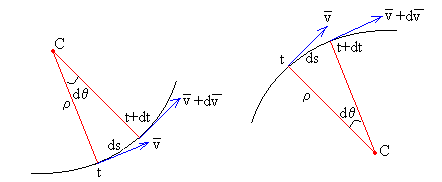
Hemos de tener en cuenta que la curvatura de la trayectoria es negativa (figura de la derecha). La curva queda a la derecha de la tangente tomada en sentido de las x crecientes. La igualdad anterior se escribe para este caso

${\displaystyle \frac{dv}{dt}=-\frac{v}{\rho }\frac{dv}{d\theta }}$

Las ecuaciones del movimiento en la dirección tangencial y en la dirección normal se convierten en una única ecuación diferencial de primer orden.

${\displaystyle \begin{array}{l}-\frac{g\cos \theta }{v}\frac{dv}{d\theta }=-g\sin \theta -fg\hfill \\ \frac{1}{v}\frac{dv}{d\theta }=\tan \theta +\frac{f}{\cos \theta }\hfill \end{array}}$

Velocidad del proyectil

Integramos la ecuación diferencial, teniendo en cuenta que en el cuerpo se lanza del origen con velocidad v₀ haciendo un ángulo θ₀ con la horizontal

${\displaystyle \begin{array}{l}{\displaystyle \underset{v_0}{\overset{v}{\int }}\frac{dv}{v}}={\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}\left(\tan \theta +\frac{f}{\cos \theta }\right)}d\theta \\ \ln \left(\frac{v}{v_0}\right)=-\ln \left(\frac{\cos \theta }{\cos {\theta }_0}\right)+f\ln \left(\frac{(1+\sin \theta )\cos {\theta }_0}{\cos \theta (1+\sin {\theta }_0)}\right)\\ v=v_0{\left(\frac{\cos {\theta }_0}{\cos \theta }\right)}^{f+1}{\left(\frac{1+\sin \theta }{1+\sin {\theta }_0}\right)}^f\end{array}}$

Se ha utilizado el resultado de la integral de la inversa del coseno

Tiempo de vuelo

ds=v·dt
ρdθ= v·dt

${\displaystyle \begin{array}{l}dt=-\frac{v}{g\cos \theta }d\theta =\\ t=-\frac{v_0}{g}\frac{{\left(\cos {\theta }_0\right)}^{f+1}}{{\left(1+\sin {\theta }_0\right)}^f}{\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}{\left(\frac{1+\sin \theta }{\cos \theta }\right)}^f\frac{d\theta }{{\cos }^2\theta }}\end{array}}$

Haciendo los cambios de variable

${\displaystyle \begin{array}{l}u=\tan \theta du=\frac{d\theta }{{\cos }^2\theta }\\ {{\displaystyle \int \left(\sqrt{1+u^2}+u\right)}}^{f}du\\ u=\sinh z\\ {{\displaystyle \int \left(\cosh z+\sinh z\right)}}^f\cosh z·dz=\frac{1}{2}{\displaystyle \int \left(e^{(f+1)z}+e^{(f-1)z}\right)}dz=\frac{e^{fz}}{2}\left(\frac{e^z}{f+1}+\frac{e^{-z}}{f-1}\right)\\ e^z=\frac{1+\sin \theta }{\cos \theta }{e}^{-z}=\frac{1-\sin \theta }{\cos \theta }\end{array}}$

llegamos al siguiente resultado

${\displaystyle \begin{array}{l}t={-\frac{v_0}{g}\frac{{\left(\cos {\theta }_0\right)}^{f+1}}{{\left(1+\sin {\theta }_0\right)}^f}\left\{\frac{{\left(1+\sin \theta \right)}^f}{{\left(\cos \theta \right)}^f}\frac{\left(f-\sin \theta \right)}{\left(f^2-1\right)\cos \theta }\right\}|}_{{\theta }_0}^{\theta }=\\ \frac{1}{f^2-1}\frac{v_0}{g}\left\{\left(f-\sin {\theta }_0\right)-{\left(\frac{\cos {\theta }_0}{\cos \theta }\right)}^{f+1}{\left(\frac{1+\sin \theta }{1+\sin {\theta }_0}\right)}^f\left(f-\sin \theta \right)\right\}\end{array}}$

Abscisa x

dx=ds·cosθ=ρdθ·cosθ

${\displaystyle \begin{array}{l}dx=-\frac{v^2}{g\cos \theta }\cos \theta ·d\theta =-\frac{v^2}{g\sin \alpha }d\theta \hfill \\ x=-\frac{v_0^2}{g}\frac{{\left(\cos {\theta }_0\right)}^{2f+2}}{{\left(1+\sin {\theta }_0\right)}^{2f}}\underset{{\theta }_0}{\overset{\theta }{{\displaystyle \int }}}{\left(\frac{1+\sin \theta }{\cos \theta }\right)}^{2f}\frac{d\theta }{{\cos }^2\theta }\hfill \end{array}}$

Haciendo los cambios de variable

${\displaystyle \begin{array}{l}u=\tan \theta du=\frac{d\theta }{{\cos }^2\theta }\\ {{\displaystyle \int \left(\sqrt{1+u^2}+u\right)}}^{2f}du\\ u=\sinh z\\ {{\displaystyle \int \left(\cosh z+\sinh z\right)}}^{2f}\cosh z·dz=\frac{1}{2}{\displaystyle \int \left(e^{(2f+1)z}+e^{(2f-1)z}\right)}dt=\frac{e^{2fz}}{2}\left(\frac{e^z}{2f+1}+\frac{e^{-z}}{2f-1}\right)\\ e^z=\frac{1+\sin \theta }{\cos \theta }{e}^{-z}=\frac{1-\sin \theta }{\cos \theta }\end{array}}$

Llegamos al siguiente resultado

${\displaystyle \begin{array}{l}x={-\frac{v_0^2}{g}\frac{{\left(\cos {\theta }_0\right)}^{2f+2}}{{\left(1+\sin {\theta }_0\right)}^{2f}}\left\{\frac{{\left(1+\sin \theta \right)}^{2f}}{{\left(\cos \theta \right)}^{2f}}\frac{\left(2f-\sin \theta \right)}{\left(4f^2-1\right)\cos \theta }\right\}|}_{{\theta }_0}^{\theta }=\\ \frac{1}{4f^2-1}\frac{v_0^2}{g}\left\{\left(2f-\sin {\theta }_0\right)\cos {\theta }_0-{\left(\frac{\cos {\theta }_0}{\cos \theta }\right)}^{2f+2}{\left(\frac{1+\sin \theta }{1+\sin {\theta }_0}\right)}^{2f}\cos \theta \left(2f-\sin \theta \right)\right\}\end{array}}$

Ordenada y

dy=ds·sinθ=ρdθ·sinθ

${\displaystyle \begin{array}{l}dy=-\frac{v^2}{g\cos \theta }\sin \theta ·d\theta =-\frac{v^2}{g\sin \alpha }\tan \theta d\theta \hfill \\ y=-\frac{v_0^2}{g}\frac{{\left(\cos {\theta }_0\right)}^{2f+2}}{{\left(1+\sin {\theta }_0\right)}^{2f}}\underset{{\theta }_0}{\overset{\theta }{{\displaystyle \int }}}{\left(\frac{1+\sin \theta }{\cos \theta }\right)}^{2f}\frac{\tan \theta }{{\cos }^2\theta }d\theta \hfill \end{array}}$

Haciendo los cambios de variable

${\displaystyle \begin{array}{l}u=\tan \theta du=\frac{d\theta }{{\cos }^2\theta }\\ {{\displaystyle \int \left(\sqrt{1+u^2}+u\right)}}^{2f}u·du\\ u=\sinh z\\ {{\displaystyle \int \left(\cosh z+\sinh z\right)}}^{2f}\sinh z·\cosh z·dz=\frac{1}{4}{\displaystyle \int \left(e^{(2f+2)z}-e^{(2f-2)z}\right)}dt=\frac{e^{2fz}}{8}\left(\frac{e^{2z}}{f+1}-\frac{e^{-2z}}{f-1}\right)\\ e^z=\frac{1+\sin \theta }{\cos \theta }{e}^{-z}=\frac{1-\sin \theta }{\cos \theta }\end{array}}$

llegamos al siguiente resultado

${\displaystyle \begin{array}{l}y={\frac{v_0^2}{g}\frac{{\left(\cos {\theta }_0\right)}^{2f+2}}{{\left(1+\sin {\theta }_0\right)}^{2f}}\left\{{\left(\frac{1+\sin \theta }{\cos \theta }\right)}^{2f}\frac{\left(2f\sin \theta -1-{\sin }^2\theta \right)}{4\left(f^2-1\right){\cos }^2\theta }\right\}|}_{{\theta }_0}^{\theta }=\\ \frac{1}{4\left(f^2-1\right)}\frac{v_0^2}{g}\left\{\left(2f\sin {\theta }_0-1-{\sin }^2{\theta }_0\right)-{\left(\frac{\cos {\theta }_0}{\cos \theta }\right)}^{2f+2}{\left(\frac{1+\sin \theta }{1+\sin {\theta }_0}\right)}^{2f}\left(2f\sin \theta -1-{\sin }^2\theta \right)\right\}\end{array}}$

Trayectorias

El punto de impacto del proyectil es (R,0), donde R es el alcance. Poniendo y=0, resolvemos la ecuación trascendente para obtener el ángulo θ.

${\displaystyle \left(2f\sin {\theta }_0-1-{\sin }^2{\theta }_0\right)-{\left(\frac{\cos {\theta }_0}{\cos \theta }\right)}^{2f+2}{\left(\frac{1+\sin \theta }{1+\sin {\theta }_0}\right)}^{2f}\left(2f\sin \theta -1-{\sin }^2\theta \right)=0}$

Conocido θ calculamos el alcance R y el tiempo de vuelo T

${\displaystyle \begin{array}{l}R=\frac{1}{4f^2-1}\frac{v_0^2}{g}\left\{\left(2f-\sin {\theta }_0\right)\cos {\theta }_0-{\left(\frac{\cos {\theta }_0}{\cos \theta }\right)}^{2f+2}{\left(\frac{1+\sin \theta }{1+\sin {\theta }_0}\right)}^{2f}\cos \theta \left(2f-\sin \theta \right)\right\}\\ T=\frac{1}{f^2-1}\frac{v_0}{g}\left\{\left(f-\sin {\theta }_0\right)-{\left(\frac{\cos {\theta }_0}{\cos \theta }\right)}^{f+1}{\left(\frac{1+\sin \theta }{1+\sin {\theta }_0}\right)}^f\left(f-\sin \theta \right)\right\}\end{array}}$

Se dispara un proyectil con velocidad v₀=50 m/s, haciendo un ángulo θ₀=π/4 (45°). Supondremos que el parámetro f=0.25. Calculamos el ángulo θ que hace la dirección de la velocidad del proyectil con el eje X en el momento en el que llega al suelo y=0, utilizando la función fzero. Dibujamos la trayectoria del proyectil y calculamos el tiempo T de vuelo y el alcance R

f=0.25; %rozamiento
v0=50; %velocidad de disparo
ang=pi/4; %ángulo de tiro

x=@(th) v0^2*((2*f-sin(ang))*cos(ang)-((cos(ang)./cos(th)).^(2*f+2)).Ç
*(((1+sin(th))/(1+sin(ang))).^(2*f)).*cos(th).*(2*f-sin(th)))/(9.8*(4*f^2-1));
y=@(th) v0^2*((2*f*sin(ang)-1-sin(ang)^2)-((cos(ang)./cos(th)).^(2*f+2)).
*(((1+sin(th))/(1+sin(ang))).^(2*f)).*(2*f*sin(th)-1-sin(th).^2))/(4*(f^2-1)*9.8);
t=@(th) v0*((f-sin(ang))-((cos(ang)./cos(th)).^(f+1)).*(((1+sin(th))/
(1+sin(ang))).^f).*(f-sin(th)))/((f^2-1)*9.8);
aFinal=fzero(y,-ang);
fplot(x,y,[aFinal,ang])
grid on
xlabel('x')
ylabel('y')
title('trayectorias')

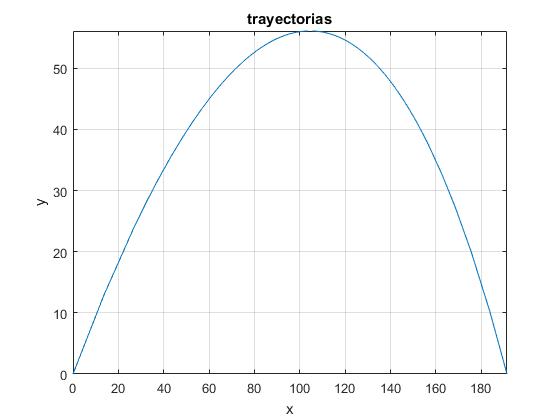
>> t(aFinal)
ans =    6.8081
>> x(aFinal)
ans =  191.3394

Mediante este script comparamos las trayectorias para tres valores diferentes del parámetro f, 0.05, 0.15 y 0.25. La velocida dde disparo es v₀=50 m/s y el ángulo de tiro θ₀=π/4 (45°)

v0=50; %velocidad de disparo
ang=pi/4; %ángulo de tiro
hold on
for f=[0.05,0.15,0.25]
    x=@(th) v0^2*((2*f-sin(ang))*cos(ang)-((cos(ang)./cos(th)).^(2*f+2)).
*(((1+sin(th))/(1+sin(ang))).^(2*f)).*cos(th).*(2*f-sin(th)))/(9.8*(4*f^2-1));
    y=@(th) v0^2*((2*f*sin(ang)-1-sin(ang)^2)-((cos(ang)./cos(th)).^(2*f+2)).
*(((1+sin(th))/(1+sin(ang))).^(2*f)).*(2*f*sin(th)-1-sin(th).^2))/(4*(f^2-1)*9.8);
    aFinal=fzero(y,-ang);
    fplot(x,y,[aFinal,ang], 'displayName',num2str(f))
end
hold off
grid on
legend('-DynamicLegend','location','northeast')
xlabel('x')
ylabel('y')
title('trayectorias')

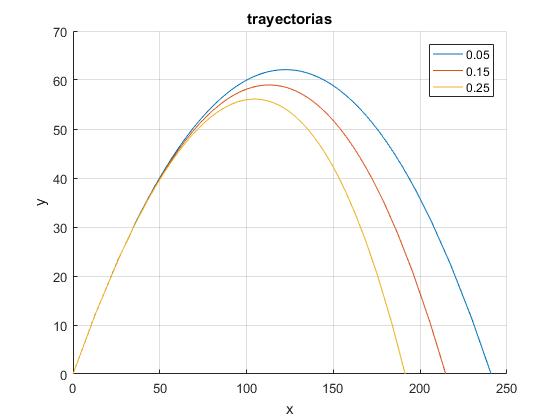
Altura máxima

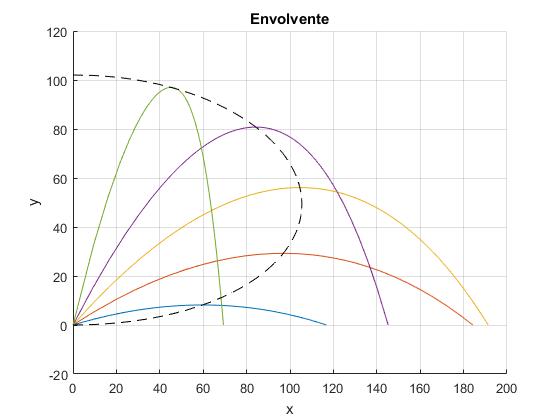
La altura máxima del proyectil se obtiene cuando el ángulo θ=0. Las coordenadas del vértice (x₁, y₁) son

${\displaystyle \begin{array}{l}{x}_1=\frac{1}{4f^2-1}\frac{v_0^2}{g}\left\{\left(2f-\sin {\theta }_0\right)\cos {\theta }_0-2f{\cos }^2{\theta }_0{\left(\frac{\cos {\theta }_0}{1+\sin {\theta }_0}\right)}^{2f}\right\}\\ y_1=\frac{1}{4\left(f^2-1\right)}\frac{v_0^2}{g}\left\{\left(2f\sin {\theta }_0-1-{\sin }^2{\theta }_0\right)+{\cos }^2{\theta }_0{\left(\frac{\cos {\theta }_0}{1+\sin {\theta }_0}\right)}^{2f}\right\}\end{array}}$

Representamos la curva que une los vértices de las trayectorias mediante una línea a trazos, junto con las trayectorias de ángulos de tiro 15°, 30°, 45°, 60°, 75°, disparados con la misma velocidad v₀=50 m/s. El parámetro f=0.25

f=0.25; %rozamiento
v0=50; %velocidad de disparo
hold on
for ang=pi/12:pi/12:pi/2-pi/12;
    x=@(th) v0^2*((2*f-sin(ang))*cos(ang)-((cos(ang)./cos(th)).^(2*f+2)).
*(((1+sin(th))/(1+sin(ang))).^(2*f)).*cos(th).*(2*f-sin(th)))/(9.8*(4*f^2-1));
    y=@(th) v0^2*((2*f*sin(ang)-1-sin(ang)^2)-((cos(ang)./cos(th)).^(2*f+2)).
*(((1+sin(th))/(1+sin(ang))).^(2*f)).*(2*f*sin(th)-1-sin(th).^2))/(4*(f^2-1)*9.8);
    aFinal=fzero(y,-ang);
    fplot(x,y,[aFinal,ang])
end
x1=@(th) v0^2*cos(th).*((2*f-sin(th))-2*f*cos(th).*(cos(th)./
(1+sin(th))).^(2*f))/(9.8*(4*f^2-1));
y1=@(th) v0^2*((2*f*sin(th)-1-sin(th).^2)+(cos(th).^2).
*(cos(th)./(1+sin(th))).^(2*f))/(9.8*4*(f^2-1));
fplot(x1,y1,[0,pi/2], 'color','k','linestyle','--')
hold off
grid on
xlabel('x')
ylabel('y')
title('Envolvente')

Casos especiales f=1 y f=0.5

En los ejemplos anteriores, el rozamiento f se mantiene pequeño, inferior a 0.5. Cuando f=0.5. El denominador de la abscisa x contiene el término (4f²-1), que se hace cero cuando f=0.5. Es preciso volver a calcular la abscisa x

Del mismo modo, para f=1, tenemos que volver a calcular la expresión del tiempo t y la expresión de la ordenada y, debido a que en el denominador contienen el término (f²-1) que se hace cero

Estos dos casos, se estudian en la página titulada Proyectil que desliza sobre un plano inclinado

Referencias