Supongamos un cuerpo simétrico como un cilindro, como vemos en la figura, las líneas de corriente se reparten simétricamente. La velocidad del fluido es nula en los extremos de su diámetro horizontal y máxima en los extremos de su diámetro vertical, pasando por valores intermedios para diámetros que tengan otra orientación.

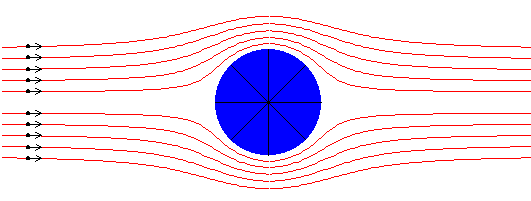
Si el fluido es ideal, las presiones se distribuyen simétricamente alrededor del cuerpo de modo que las fuerzas debidas a la presión se anulan de dos en dos en los extremos de cada diámetro. La resultante de las fuerzas que ejerce el fluido sobre el cuerpo es nula. Por tanto, se dará la paradoja de que un cuerpo simétrico no es arrastrado cuando se coloca en el seno de una corriente de un fluido perfecto.

Como hemos visto al explicar la fórmula de Stokes, en un fluido real, el cuerpo sufre por parte del medio una resistencia que depende de su velocidad relativa y de su forma.

Efecto Magnus

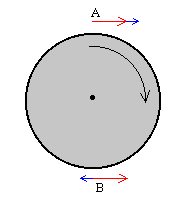
Sea un cilindro que gira en el sentido de las agujas del reloj, y que está colocado perpendicularmente a las líneas de corriente de un fluido en régimen laminar con velocidad constante.

Por efecto de la viscosidad, los elementos de un fluido que se encuentran en contacto con la superficie límite, son arrastrados por el movimiento de giro del cilindro, de tal forma que en la parte superior del cilindro A los elementos de fluido aumentarán de velocidad y en cambio, en la parte inferior B su velocidad disminuirá tal como se ve en la figura.

De acuerdo con la ecuación de Bernoulli la presión en A será menor que en B, el mismo razonamiento se aplica a otros puntos del fluido por encima y por debajo de la línea horizontal que pasa por el centro del cilindro. La resultante de todas las fuerzas que actúan sobre el cilindro debido a la presión del fluido es una fuerza vertical denominada sustentación que tiende a desplazar al cilindro en una dirección perpendicular a las líneas de corriente.

El efecto Magnus se explica en términos de la función corriente Ψ(x, y). Las líneas de corriente, (en color rojo), son aquellas para las que Ψ(x, y)=cte.

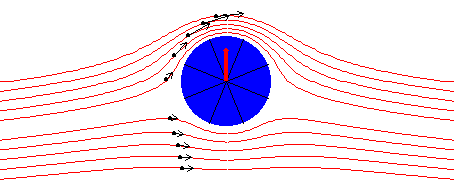
El campo de velocidades se obtiene derivando (derivada parcial) la función corriente. La velocidad tangencial se obtiene

${\displaystyle v_{\theta }=\frac{1}{r}\frac{\partial \Psi }{\partial r}}$

que se representa mediante flechas de color negro que acompañan a las partículas de fluido.

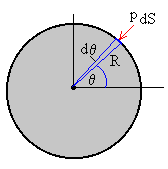
De acuerdo al teorema de Bernoulli la presión de un fluido con velocidad v es p=ρv²/2. Donde ρ es la densidad constante de un fluido incompresible. La fuerza debida a la presión se aplica perpendicularmente a la superficie, de modo que la componente vertical de la fuerza es -sinθ·p(θ)·dS tal como se ve en la figura.

Siendo dS el elemento de superficie dS=L·R·dθ , para un cilindro de longitud L y radio R. La fuerza neta se obtiene integrando respecto del ángulo θ entre 0 y 2π .

La fuerza neta por unidad de longitud del cilindro denominada sustentación, viene dada por la fórmula de Kutta-Joukowski

F=ρ v₀Γ

Siendo v₀ la velocidad del fluido en el infinito (cuando no experimenta la influencia del cilindro) y Γ se denomina circulación del campo de velocidades alrededor de cualquier línea cerrada que rodee al cuerpo sólido.

Actividades

Mostramos las líneas de corriente de un fluido en régimen laminar y un cilindro que gira con velocidad angular ω, en sentido horario.

Se introduce

• el valor de un parámetro que representa la circulación que se añade a un fluido en régimen laminar.

Se pulsa el botón titulado Nuevo

Así, podemos comparar el trazado de las líneas de corriente cuando el valor de la circulación es cero (el cilindro no gira), con las líneas de corriente cuando la circulación Γ es distinta de cero (el cilindro gira con una velocidad angular proporcional al parámetro circulación). Apreciamos que los puntos de estancamiento (velocidad nula del fluido) se han desplazado hacia la parte inferior del cilindro.

Cuando se hace girar el cilindro, se representa mediante una flecha con origen en el centro del cilindro la sustentación F.

Movimiento de una esfera

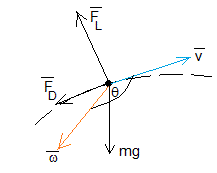
Cuando un cuerpo de forma esférica (una pelota de tenis, beisbol, etc.), se mueve en el aire experimenta tres fuerzas

• El peso, mg
• Una fuerza de rozamiento, F_D proporcional al cuadrado de la velocidad, cuya dirección es la de la velocidad y de sentido contrario
• Si la esfera tiene un movimiento de rotación con velocidad angular ω alrededor de un eje, experimenta una fuerza de sustentación debida al efecto Magnus, F_L, en una dirección que es perpendicular al producto vectorial $\overrightarrow{\omega }\times \overrightarrow{v}$

Fuerza de rozamiento

La fuerza de rozamiento F_D proporcional al cuadrado de la velocidad es

${\displaystyle F_D=\frac{1}{2}\rho A{C}_D{v}^2}$

Donde C_D se denomina coeficiente de arrastre, ρ es la densidad del fluido, A es el área de la sección transversal a la dirección del movimiento (en el caso de una esfera es πd²/4) y v es la velocidad relativa del objeto respecto del fluido.

El coeficiente de arrastre es una función del número de Reynolds, Re. Para números de Reynolds en el intervalo aproximadamente 10³ a 3·10⁵, C_D es casi constante y vale 0.45, a partir de Re 3·10⁵, C_D disminuye rápidamente ya que capa de fluido que rodea al cuerpo que se mueve experimenta una transición del régimen laminar al turbulento. C_D cambia en general, con la velocidad v de traslación y con la velocidad ω de rotación del cuerpo esférico.

En forma vectorial, la fuerza de rozamiento es

${\displaystyle \overrightarrow{F_r}=-\frac{1}{2}\rho A{C}_{D}v·\overrightarrow{v}}$

Fuerza de sustentación

La fuerza de sustentación F_L debida al efecto Magnus es proporcional al cuadrado de la velocidad

${\displaystyle F_L=\frac{1}{2}\rho A{C}_L{v}^2}$

Donde C_L es un coeficiente que depende, en general, de la velocidad angular de rotación ω. Para las pelotas de golf

${\displaystyle C_L=0.319\left(1-\exp (-0.00248·\omega \right)}$

La dirección de la fuerza F_L es la que corresponde al producto vectorial $\overrightarrow{\omega }\times \overrightarrow{v}$. En forma vectorial

${\displaystyle \overrightarrow{F_L}=\frac{1}{2}\rho A{C}_{L}v\left(\frac{\overrightarrow{\omega }\times \overrightarrow{v}}{\omega }\right)}$

Ecuaciones del movimiento

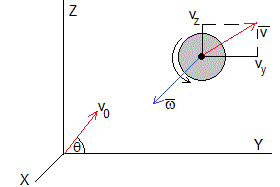
Sea $\overrightarrow{v}$, la velocidad del proyectil y $\overrightarrow{W}$, la velocidad del viento. La velocidad del proyectil relativa a la del viento, $\overrightarrow{v}-\overrightarrow{W}$ determina la magnitud y dirección de la fuerza de rozamiento $\overrightarrow{F_D}$ y la fuerza de sustentación, $\overrightarrow{F_L}$

La ecuación del movimiento se escribe

${\displaystyle \begin{array}{l}m\frac{d^2\overrightarrow{r}}{d{t}^2}=m\overrightarrow{g}+\overrightarrow{F_D}+\overrightarrow{F_L}\\ m\frac{d^2\overrightarrow{r}}{d{t}^2}=m\overrightarrow{g}-\frac{1}{2}\rho A{C}_D\left|\overrightarrow{v}-\overrightarrow{W}\right|\left(\overrightarrow{v}-\overrightarrow{W}\right)+\frac{1}{2}\rho A{C}_L\left|\overrightarrow{v}-\overrightarrow{W}\right|\left\{\frac{\overrightarrow{\omega }\times \left(\overrightarrow{v}-\overrightarrow{W}\right)}{\omega }\right\}\end{array}}$

que equivale a tres ecuaciones diferenciales

${\displaystyle \begin{array}{l}m\frac{d^{2}x}{d{t}^2}=-\frac{1}{2}\rho A\left|\overrightarrow{v}-\overrightarrow{W}\right|\left\{C_D\left(v_x-W_x\right)-C_L\frac{{\omega }_y(v_z-W_z)-{\omega }_z(v_y-W_y)}{\omega }\right\}\\ m\frac{d^{2}y}{d{t}^2}=-\frac{1}{2}\rho A\left|\overrightarrow{v}-\overrightarrow{W}\right|\left\{C_D\left(v_y-W_y\right)-C_L\frac{{\omega }_z(v_x-W_x)-{\omega }_x(v_z-W_z)}{\omega }\right\}\\ m\frac{d^{2}z}{d{t}^2}=-\frac{1}{2}\rho A\left|\overrightarrow{v}-\overrightarrow{W}\right|\left\{C_D\left(v_z-W_z\right)-C_L\frac{{\omega }_x(v_y-W_y)-{\omega }_y(v_x-W_x)}{\omega }\right\}-mg\\ \left|\overrightarrow{v}-\overrightarrow{W}\right|=\sqrt{{\left(v_x-W_x\right)}^2+{\left(v_y-W_y\right)}^2+{\left(v_z-W_z\right)}^2}\end{array}}$

Para resolver este sistema de ecuaciones diferenciales, precisamos:

• La posición inicial del proyectil, x(0), y(0) y z(0) en el instante t=0
• La velocidad inicial del proyectil, v_x(0), v_y(0) y v_z(0) en el instante t=0
• Las componentes W_x, W_y y W_z de la velocidad del viento que se supondrá constante en todos los puntos (x,y,z) y que no cambiará con el tiempo t.
• Las componentes de la velocidad angular de rotación del cuerpo esférico, ω_x, ω_y y ω_z que se supondrán constantes para todos los valores de t. Es decir, el módulo de la velocidad angular de rotación y la dirección del eje de rotación permanecerán invariables.

Ejemplos

Supondremos en todos los casos que que no hay viento, de modo que $\overrightarrow{W}=0$. El sistema de tres ecuaciones diferenciales se convierte en

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}=-\frac{1}{2m}\rho Av\left\{C_D{v}_x-C_L\frac{{\omega }_y{v}_z-{\omega }_z{v}_y}{\omega }\right\}\\ \frac{d^{2}y}{d{t}^2}=-\frac{1}{2m}\rho Av\left\{C_D{v}_y-C_L\frac{{\omega }_z{v}_x-{\omega }_x{v}_z}{\omega }\right\}\\ \frac{d^{2}z}{d{t}^2}=-\frac{1}{2m}\rho Av\left\{C_D{v}_z-C_L\frac{{\omega }_x{v}_y-{\omega }_y{v}_x}{\omega }\right\}-g\\ v=\sqrt{v_x^2+v_y^2+v_z^2}\omega =\sqrt{{\omega }_x^2+{\omega }_y^2+{\omega }_z^2}\end{array}}$

Creamos una función para integrar el sistema de tres ecuaciones diferenciales mediante el procedimiento ode45. Cuando la velocidad angular de rotación ω=0, se produce un cociente 0/0 en el término correspondiente a la fuerza de sustentación, que hay que evitarlo tal como se muestra en el código

function der = magnus_proyectil(~,x)
    global w;  %vector velocidad angular de rotación paralela al eje X 
    D=7.2008e-2; % diámetro
    m=1.5947e-1; % masa
    k=1.22*pi*D^2/(8*m);
    Cd=0.45;
    wRot=sqrt(w(1)^2+w(2)^2+w(3)^2);
    Cl=0.3187*(1-exp(-2.483e-3*wRot));
    %x(1) es y, x(2) es  dy/dt, x(3) es z, x(4) es dz/dt
    v=sqrt(x(2)^2 + x(4)^2+x(6)^2); %velocidad
    if wRot~=0
        der = [x(2); -k*v*(Cd*x(2)-Cl*(w(2)*x(6)-w(3)*x(4))/wRot); x(4);
 -k*v*(Cd*x(4)-Cl*(w(3)*x(2)-w(1)*x(6))/wRot); x(6);
-9.8-k*v*(Cd*x(6)-Cl*(w(1)*x(4)-w(2)*x(2))/wRot)];
    else
        der = [x(2); -k*v*Cd*x(2); x(4); -k*v*Cd*x(4); x(6);-9.8-k*v*Cd*x(6)];
end

Movimiento en el plano Y-Z

Estudiamos primero, los casos más sencillos

• El eje de rotación es paralelo al eje X, ω_y=0, ω_z=0
• La velocidad inicial a lo largo del eje X es nula, v_x=0

Consideremos dos casos: en el primero, la dirección de la velocidad incial es paralela al eje Y, en el segundo, la dirección de velocidad inicial es paralela al eje Z

Creamos un script en el que llamamos al procedimiento ode45 para integrar el sistema de tres ecuaciones diferenciales, y representar gráficamente, la posición (y,z) del proyectil en función del tiempo t.

En primer lugar, definimos el vector velocidad angular de rotación w: [ω_x, ω_y, ω_z];

Especificamos las condiciones iniciales, en un vector x0 de dimensión 6: x0=[x(0), v_x(0), y(0), v_y(0), z(0), v_z(0)];

global w;
w=[600,0,0]; %velocidad angular de rotación paralela al eje X
%condiciones iniciales, parte del origen con vy(0)=60 m/s
%x0=[x(0),vx(0),y(0),vy(0),z(0),vz(0)];
x0=[0,0,0,60,0,0];
[t,x]=ode45(@magnus_proyectil,[0,1.2],x0);
hold on
plot(t, x(:,3)) %y-t
plot(t, x(:,5)) %z-t
hold off
grid on
ylim([-5,20])
legend('y','z')
xlabel('t')
ylabel('y,z');
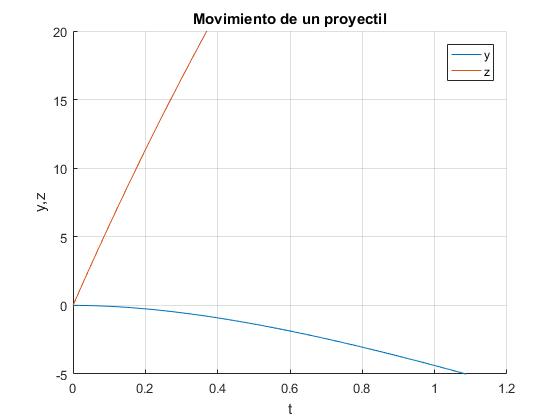
title('Movimiento de un proyectil')

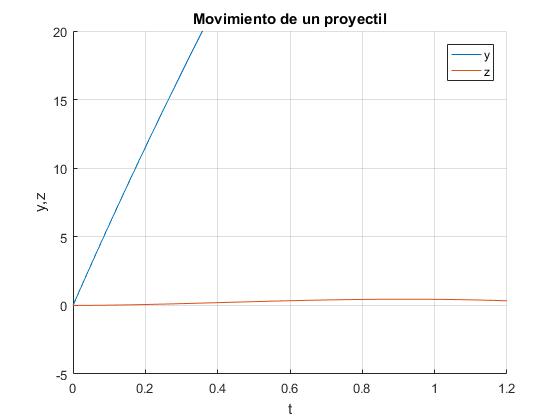
• Sea v_y(0)=60 m/s, v_z(0)=0, ω_x=600 rad/s

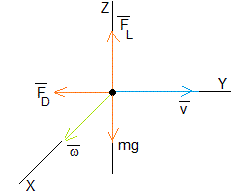
En la figura, se representan las fuerzas sobre el proyectil. La fuerza de rozamiento F_D disminuye el desplazamiento a lo largo del eje Y, y la fuerza de sustentación F_L provoca un pequeño desplazamiento a lo largo del eje Z





• Sea v_y(0)=0, v_z(0)=60 m/s, ω_x=600 rad/s

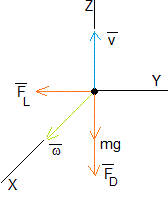
En la figura, se representan las fuerzas sobre el proyectil. La fuerza de sustentación F_L provoca un desplazamiento a lo largo del eje Y en sentido negativo

Trayectorias

Para trazar la trayectoria interrumpimos el proceso de integración del sistema de ecuaciones diferenciales cuando el proyectil llega al suelo, z=0. Para ello, definimos la siguiente función que se la pasamos al procedimiento ode45

function [detect,stopin,direction]=stop_magnus_1(~,x)
    detect=x(5); %z
    stopin=1; 
    direction=-1; 
end

Creamos un script para trazar la trayectoria de un proyectil disparado con velocidad v₀=60 m/s haciendo un ángulo de tiro θ=12°. La velocidad angular de rotación es paralela al eje Y, en un caso ω_y=+300 rad/s en en otro caso, ω_y=-300 rad/s. Comparamos estas dos trayectorias con la que seguiría un proyectil con velocidad angular de rotación nula ω=0, es decir, bajo la acción de un fuerza de rozamiento proporcional al cuadrado de la velocidad y también, con la trayectoria que seguiría un proyectil sin rozamiento, es decir, la trayectoria parabólica ideal. En una sola imagen, apreciamos el efecto de la velocidad angular de rotación (y del sentido de la misma) y de la fuerza de rozamiento proporcional al cuadrado de la velocidad en comparación con la trayectoria ideal parabólica

global w;
%x0=[x(0),vx(0),y(0),vy(0),z(0),vz(0)];
%condiciones iniciales, 
th=12*pi/180; % ángulo de disparo 
v0=60; %velocidad inicial
x0=[0,v0*cos(th),0,0,0,v0*sin(th)]; 
T=v0*sin(th)/4.9; %tiempo sin rozamiento

opts=odeset('events',@stop_magnus_1);
w=[0,300,0]; %velocidad angular de rotación paralela al eje Y
[t,x]=ode45(@magnus_proyectil,[0,2*T],x0, opts);
w=[0,-300,0]; %velocidad angular de rotación paralela al eje Y
[t,x1]=ode45(@magnus_proyectil,[0,2*T],x0, opts);
w=[0,0,0]; %sin rotación
[t,xp]=ode45(@magnus_proyectil,[0,2*T],x0, opts);

hold on
plot(x(:,1), x(:,5)) %x-z con rotación wy=+300
plot(x1(:,1), x1(:,5)) %x-z con rotación wy=-300
plot(xp(:,1), xp(:,5)) %x-z sin rotación w=0
fplot(@(t) v0*cos(th)*t, @(t) v0*sin(th)*t-4.9*t.^2, [0,T]) %parabólica
hold off
grid on
ylim([0,12])
legend('\omega=+300','\omega=-300','\omega=0','ideal')
xlabel('x')
ylabel('z');
title('Trayectoria del proyectil')

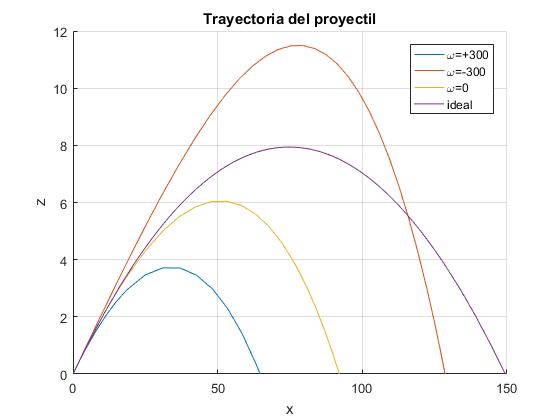
Con las mismas condiciones iniciales que en el ejemplo anterior, se comparan trayectorias con distintas velocidades angulares y direcciones: ω_y=-300 rad/s (representada en la figura anterior), ω_y=212 rad/s y ω_z=212 rad/s, ω_z=300 rad/s, ω_y=-212 rad/s y ω_z=-212 rad/s, ω_z=-300 rad/s

global w;
%x0=[x(0),vx(0),y(0),vy(0),z(0),vz(0)];
%condiciones iniciales, 
th=12*pi/180; % ángulo de disparo 
v0=60; %velocidad inicial
x0=[0,v0*cos(th),0,0,0,v0*sin(th)]; 
T=v0*sin(th)/4.9; %tiempo sin rozamiento

opts=odeset('events',@stop_magnus_1);
w=[0,-300,0]; %velocidad angular de rotación paralela al eje Y
[t,x]=ode45(@magnus_proyectil,[0,2*T],x0, opts);
w=[0,212,212]; %velocidad angular de rotación 
[t,x1]=ode45(@magnus_proyectil,[0,2*T],x0, opts);
w=[0,0, 300]; %velocidad angular de rotación paralela al eje Z
[t,x2]=ode45(@magnus_proyectil,[0,2*T],x0, opts);
w=[0,-212,-212]; %velocidad angular de rotación 
[t,x3]=ode45(@magnus_proyectil,[0,2*T],x0, opts);
w=[0,0,-300]; %velocidad angular de rotación paralela al eje Z
[t,x4]=ode45(@magnus_proyectil,[0,2*T],x0, opts);

hold on
plot(x(:,1), x(:,5)) 
plot(x1(:,1), x1(:,5)) 
plot(x2(:,1), x2(:,5)) 
plot(x3(:,1), x3(:,5)) 
plot(x4(:,1), x4(:,5)) 
fplot(@(t) v0*cos(th)*t, @(t) v0*sin(th)*t-4.9*t.^2, [0,T]) %parabólica
hold off
grid on
%ylim([0,12])
legend('\omega_y=-300','\omega_y=212,\omega_z=212','\omega_z=300',
'\omega_y=-212,\omega_z=-212','\omega_z=-300','ideal')
xlabel('x')
ylabel('z');
title('Trayectoria del proyectil')

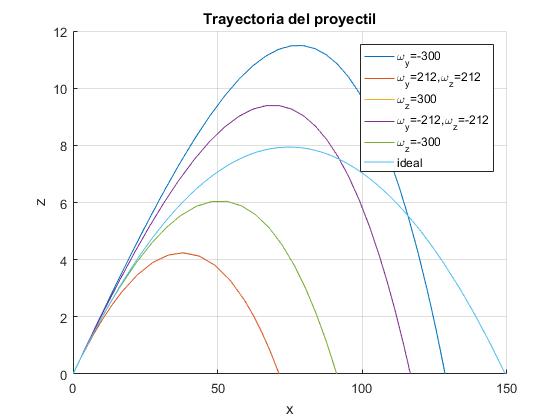
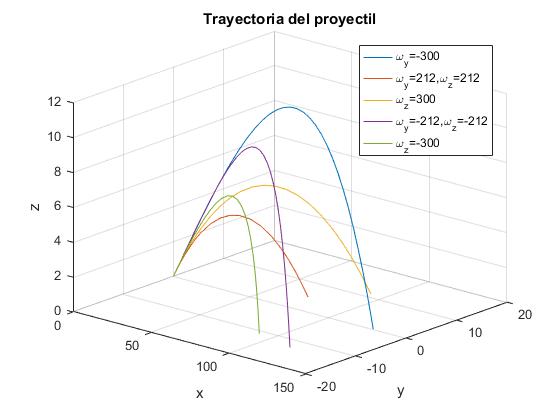
Las trayectorias correspondientes a ω_z=+300 rad/s y ω_z=-300 rad/s se superponen en el plano X-Z, pero no coinciden en el espacio (son simétricas). Véase la figura más abajo.

Mostramos estas mismas trayectorias (excepto la que corresponde a la trayectoria ideal parabólica) en tres dimensiones

global w;
%x0=[x(0),vx(0),y(0),vy(0),z(0),vz(0)];
%condiciones iniciales, 
th=12*pi/180; % ángulo de disparo 
v0=60; %velocidad inicial
x0=[0,v0*cos(th),0,0,0,v0*sin(th)]; 
T=v0*sin(th)/4.9; %tiempo sin rozamiento

opts=odeset('events',@stop_magnus_1);
w=[0,-300,0]; %velocidad angular de rotación paralela al eje Y
[t,x]=ode45(@magnus_proyectil,[0,2*T],x0, opts);
w=[0,212,212]; %velocidad angular de rotación 
[t,x1]=ode45(@magnus_proyectil,[0,2*T],x0, opts);
w=[0,0, 300]; %velocidad angular de rotación paralela al eje Z
[t,x2]=ode45(@magnus_proyectil,[0,2*T],x0, opts);
w=[0,-212,-212]; %velocidad angular de rotación 
[t,x3]=ode45(@magnus_proyectil,[0,2*T],x0, opts);
w=[0,0,-300]; %velocidad angular de rotación paralela al eje Z
[t,x4]=ode45(@magnus_proyectil,[0,2*T],x0, opts);

hold on
plot3(x(:,1), x(:,3), x(:,5)) 
plot3(x1(:,1), x1(:,3), x1(:,5)) 
plot3(x2(:,1), x2(:,3), x2(:,5)) 
plot3(x3(:,1), x3(:,3), x3(:,5)) 
plot3(x4(:,1), x4(:,3), x4(:,5)) 
hold off
grid on
zlim([0,12])
legend('\omega_y=-300','\omega_y=212,\omega_z=212','\omega_z=300',
'\omega_y=-212,\omega_z=-212','\omega_z=-300')
xlabel('x')
ylabel('y');
zlabel('z')
title('Trayectoria del proyectil')
view(50,20)

Otras expresiones para los coeficientes C_D y C_L

En general, los coeficientes C_D=f(w/v,Re) y C_L=g(w/v,Re) son funciones de w/v y Re, donde Re es el número de Reynolds, w=ωR es la velocidad (lineal) en el ecuador de la esfera que gira y v es la velocidad del centro de la esfera.

En el segundo artículo citado en las referencias, se proporcionan dos expresiones para los coeficientes C_D y C_L, válidas para los siguientes intervalos de velocidades 13.6<v<28 m/s y velocidades angulares de rotación 800<ω<3250 rpm, el ajuste no lineal a los datos experimentales, produjo los siguientes modelos de función

${\displaystyle \begin{array}{l}{C}_D=0.508+\frac{1}{{\left(22.503+4.196{\left(w/v\right)}^{-5/2}\right)}^{2/5}}\\ C_L=\frac{1}{2.202+0.981{\left(w/v\right)}^{-1}}\end{array}}$

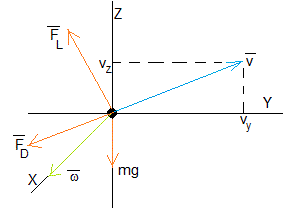
En muchos casos:

• El eje de rotación es paralelo al eje X, ω_y=0, ω_z=0
• La velocidad inicial a lo largo del eje X es nula, v_x=0

Las fuerzas sobre la esfera se muestran en la figura, el movimiento se produce en el plano Y-Z y las ecuaciones del movimiento son

${\displaystyle \begin{array}{l}\frac{d^{2}y}{d{t}^2}=-\frac{1}{2m}\rho Av\left\{C_D{v}_y+C_L\frac{{\omega }_x}{\omega }{v}_z\right\}\\ \frac{d^{2}z}{d{t}^2}=-\frac{1}{2m}\rho Av\left\{C_D{v}_z-C_L\frac{{\omega }_x}{\omega }{v}_y\right\}-g\end{array}}$

La componente ω_x, puede ser positiva o negativa, pero el módulo ω es siempre positivo. El cociente ω_x/ω es el signo de la velocidad angular de rotación.

Para integrar el sistema de dos ecuaciones diferenciales, mediante el procedimiento ode45, definimos la función

function der=pelota_tenis(~,x)
    global alpha w signo
    v = sqrt(x(2)^2 + x(4)^2);
    Cd = (0.508 + 1/(22.503 + 4.196*(v/w)^2.5)^0.4)*alpha*v;
    Cl = alpha*v/(2.022+ 0.981*v/w);
    %x(1) es y, x(2) es  dy/dt, x(3) es z, x(4) es dz/dt
    der = [x(2); -Cd*x(2)-signo*Cl*x(4); x(4);-9.8-Cd*x(4)+signo*Cl*x(2)];
  end

Para detener el proceso de integración cuando la esfera llegue al suelo, definimos la siguiente función y se la pasamos al procedimiento ode45

function [detect,stopin,direction]=stop_pelota_tenis(~,x)
    detect=x(3); 
    stopin=1; 
    direction=-1; 
end

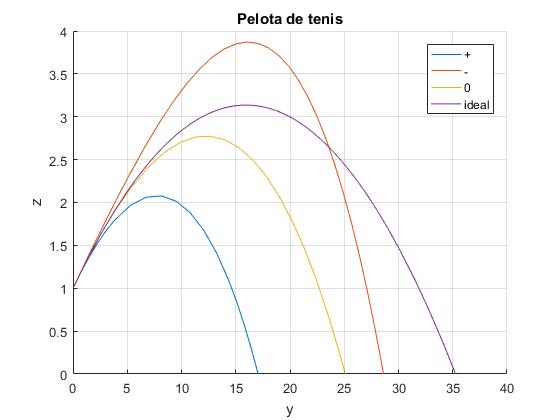
Consideremos una pelota de diámetro d=0.063 m, de masa m=0.05 kg. La densidad del aire es ρ=1.29 kg/m³. Lanzamos la pelota desde una altura h=1 m con una velocidad de v₀=25 m/s, haciendo un ángulo θ=15° con la horizontal. Le proporcionamos un movimiento de rotación de modo que el eje de giro es paralelo al eje X y la velocidad en el ecuador de la pelota es constante e igual a w=20 m/s.

Elaboramos un script, para representar gráficamente la trayectoria de la pelota

• Cuando gira con velocidad angular constante en un sentido
• Cuando gira con la misma velocidad angular constante en sentido contrario
• Cuando no gira, ω=0, su movimiento está afectado por la fuerza de rozamiento proporcional al cuadrado de la velocidad
• Cuando describe una parábola, sin rozamiento ni giro

function magnus
    d=0.063; %diámetro 
    m=0.05; %masa
    rho=1.29; %densidad del aire
    w=20; %velocidad angular de rotación constante
    alpha=pi*d^2*rho/(8*m);
    
    %condiciones iniciales,
    th=15*pi/180; % ángulo de disparo 
    v0=25; %velocidad inicial
    h=1; %altura de disparo
    x0=[0,v0*cos(th),h,v0*sin(th)];
    T=(v0*sin(th)+sqrt((v0*sin(th))^2+2*9.8*h))/9.8; %tiempo sin rozamiento
   
    opts=odeset('events',@stop_pelota_tenis);
    signo=-1;
    [~,x]=ode45(@pelota_tenis,[0,2*T],x0,opts);
    signo=1;
    [~,x1]=ode45(@pelota_tenis,[0,2*T],x0,opts);
    w=0;
    [~,x2]=ode45(@pelota_tenis,[0,2*T],x0,opts);
    hold on
    plot(x(:,1),x(:,3)) %gira en un sentido
    plot(x1(:,1),x1(:,3)) %gira en sentido opuesto
    plot(x2(:,1),x2(:,3)) %sin rotación
    fplot(@(t) v0*cos(th)*t, @(t) h+v0*sin(th)*t-4.9*t.^2, [0,T]) %parabólica
    hold off
    legend('+','-','0','ideal')
    grid on
    xlabel('y')
    ylabel('z');
    title('Pelota de tenis')

    function der=pelota_tenis(~,x)
        v = sqrt(x(2)^2 + x(4)^2);
        Cd = (0.508 + 1/(22.503 + 4.196*(v/w)^2.5)^0.4)*alpha*v;
        Cl = alpha*v/(2.022+ 0.981*v/w);
        %x(1) es y, x(2) es  dy/dt, x(3) es z, x(4) es dz/dt
        der = [x(2); -Cd*x(2)-signo*Cl*x(4); x(4);-9.8-Cd*x(4)+signo*Cl*x(2)];
      end
    
    function [detect,stopin,direction]=stop_pelota_tenis(~,x)
        detect=x(3); 
        stopin=1; 
        direction=-1; 
    end
end

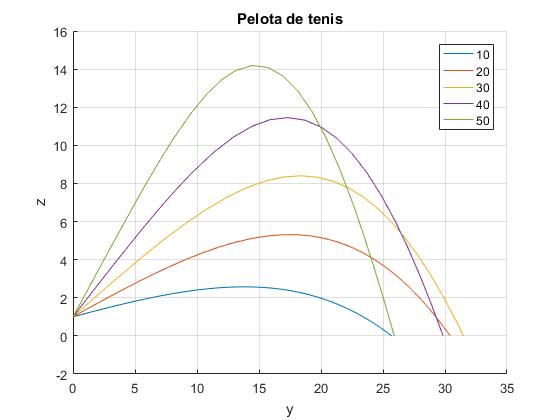
Dibujamos las trayectorias para varios ángulos de tiro, cuando la pelota gira con la misma velocidad angular constante en un sentido

function magnus_2
    d=0.063; %diámetro 
    m=0.05; %masa
    rho=1.29; %densidad del aire
    w=20; %velocidad angular de rotación constante
    alpha=pi*d^2*rho/(8*m);
    
    %condiciones iniciales,
    v0=25; %velocidad inicial
    h=1; %altura de disparo
    opts=odeset('events',@stop_pelota_tenis);
    signo=1;
    hold on
    for th=(10:10:50)*pi/180
        x0=[0,v0*cos(th),h,v0*sin(th)];
        T=(v0*sin(th)+sqrt((v0*sin(th))^2+2*9.8*h))/9.8; %tiempo sin rozamiento
        [~,x]=ode45(@pelota_tenis,[0,2*T],x0,opts);
        plot(x(:,1),x(:,3),'displayName',num2str(th*180/pi)) %gira en un sentido
    end
    legend('-DynamicLegend','location','northeast')
    hold off
    grid on
    xlabel('y')
    ylabel('z');
    title('Pelota de tenis')

    function der=pelota_tenis(~,x)
        v = sqrt(x(2)^2 + x(4)^2);
        Cd = (0.508 + 1/(22.503 + 4.196*(v/w)^2.5)^0.4)*alpha*v;
        Cl = alpha*v/(2.022+ 0.981*v/w);
        %x(1) es y, x(2) es  dy/dt, x(3) es z, x(4) es dz/dt
        der = [x(2); -Cd*x(2)-signo*Cl*x(4); x(4);-9.8-Cd*x(4)+signo*Cl*x(2)];
      end
    
    function [detect,stopin,direction]=stop_pelota_tenis(~,x)
        detect=x(3); 
        stopin=1; 
        direction=-1; 
    end
end

Trayectorias de una pelota de béisbol

Consideremos una pelota de beísbol de radio r=37 mm y masa m=0.145 kg. La densidad del aire es ρ=1.21 kg/m³ y la aceleración de la gravedad local es g=9.807 m/s²

Supondremos que no hay viento en el momento del lanzamiento de la pelota

Supondremos que el eje de rotación de la pelota es paralelo al eje X, de modo que la trayectoria de la pelota está contenida en el plano YZ

Rozamiento

La fuerza de rozamiento es proporcional al cuadrado de la velocidad, su dirección es la misma que la del vector velocidad y de sentido contrario

${\displaystyle \begin{array}{l}\overrightarrow{F_r}=-\frac{1}{2}\rho A{C}_{D}v·\overrightarrow{v}\\ \{\begin{array}{l}{F}_{ry}=-\frac{1}{2}\rho A{C}_{D}v{v}_y\\ F_{rz}=-\frac{1}{2}\rho A{C}_{D}v{v}_z\end{array}\\ C_D=0.5-\frac{0.277}{1+\exp \left(-\frac{3.28v-104.5}{20.2}\right)}\end{array}}$

A=πr² es la sección trasversal de la pelota de forma esférica de radio r

Efecto Magnus

${\displaystyle \begin{array}{l}\overrightarrow{F_L}=\frac{1}{2}\rho A{C}_{L}v\left(\frac{\overrightarrow{\omega }\times \overrightarrow{v}}{\omega }\right)\\ \overrightarrow{\omega }\times \overrightarrow{v}=\left|\begin{array}{ccc}\widehat{i}& \widehat{j}& \widehat{k}\\ \omega & 0& 0\\ 0& v_y& v_z\end{array}\right|=\omega \left(-v_z\widehat{j}+v_y\widehat{k}\right)\\ \overrightarrow{F_L}=\frac{1}{2}\rho A{C}_{L}v\left(-v_z\widehat{j}+v_y\widehat{k}\right)\\ \{\begin{array}{l}{F}_{Ly}=-\frac{1}{2}\rho A{C}_{L}v{v}_z\\ F_{Lz}=\frac{1}{2}\rho A{C}_{L}v{v}_y\end{array}\\ C_L=\frac{1.120·s}{0.583+2.333·s},s=\frac{r\omega }{v}\end{array}}$

Ecuaciones del movimiento de la pelota

${\displaystyle \begin{array}{l}\{\begin{array}{l}m\frac{d^{2}y}{d{t}^2}=-\frac{1}{2}\rho A{C}_{D}v{v}_y-\frac{1}{2}\rho A{C}_{L}v{v}_z\\ m\frac{d^{2}z}{d{t}^2}=-mg-\frac{1}{2}\rho A{C}_{D}v{v}_z+\frac{1}{2}\rho A{C}_{L}v{v}_y\end{array}\\ \{\begin{array}{l}\frac{d^{2}y}{d{t}^2}=-\frac{\rho Av}{2m}\left(C_D{v}_y+C_L{v}_z\right)\\ \frac{d^{2}z}{d{t}^2}=-g-\frac{\rho Av}{2m}\left(C_D{v}_z-C_L{v}_y\right)\end{array}\end{array}}$

Nota: las fórmulas de C_D y C_L, (3) y (5) no son las mismas en el texto del artículo de Donald C. Warren que en el material suplementario. Se reproduce la figura 3 del artículo con las fórmulas del código

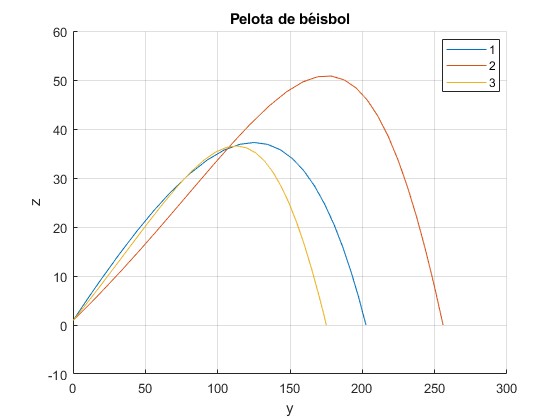
Representamos las trayectorias de la pelota lanzada desde una altura h=0.9 m, para tres casos

1. v₀=73.6 m/s, θ=24° y ω=500 rpm;
2. v₀=86.7 m/s, θ=16° y ω=2000 rpm;
3. v₀=58.8 m/s, θ=20° y ω=3000 rpm;

function magnus_1
    r=37/1000; %radio  pelota
    m=0.145; %masa
    rho=1.21; %densidad del aire
    %condiciones iniciales,
    h=0.9; %altura de disparo
   
    opts=odeset('events',@stop_pelota_tenis);
    v0=73.6; th=24*pi/180; w=500*2*pi/60;
    x0=[0,v0*cos(th),h,v0*sin(th)];
    T=(v0*sin(th)+sqrt((v0*sin(th))^2+2*9.8*h))/9.8; %tiempo sin rozamiento    
    [~,x]=ode45(@pelota_beisbol,[0,2*T],x0,opts);
     
    v0=86.7; th=16*pi/180; w=2000*2*pi/60;
    x0=[0,v0*cos(th),h,v0*sin(th)];
    T=(v0*sin(th)+sqrt((v0*sin(th))^2+2*9.8*h))/9.8; %tiempo sin rozamiento    
    [~,x1]=ode45(@pelota_beisbol,[0,3*T],x0,opts);
    
    v0=58.8; th=20*pi/180; w=3000*2*pi/60;
    x0=[0,v0*cos(th),h,v0*sin(th)];
    T=(v0*sin(th)+sqrt((v0*sin(th))^2+2*9.8*h))/9.8; %tiempo sin rozamiento    
    [~,x2]=ode45(@pelota_beisbol,[0,3*T],x0,opts);
    hold on
    plot(x(:,1),x(:,3)) 
    plot(x1(:,1),x1(:,3)) 
    plot(x2(:,1),x2(:,3)) 
    hold off
    grid on
    legend('1','2','3','location','best')
    xlabel('y')
    ylabel('z');
    title('Pelota de béisbol')

    function der=pelota_beisbol(~,x)
        v=sqrt(x(2)^2 + x(4)^2);
        A=pi*r^2; %área frontal
        Cd=0.5-0.227/(1+exp(-(v*3.28-104.5)/20.2));
        s=r*w/v;
        Cl=1.120*s/(0.583 + 2.333*s);
        %x(1) es y, x(2) es  dy/dt, x(3) es z, x(4) es dz/dt
        der=[x(2); -rho*A*v*(Cd*x(2)+Cl*x(4))/(2*m); x(4);
-9.807-rho*A*v*(Cd*x(4)-Cl*x(2))/(2*m)];
      end
    
    function [detect,stopin,direction]=stop_pelota_tenis(~,x)
        detect=x(3); 
        stopin=1; 
        direction=-1; 
    end
end

Referencias

Garry Robinson, Ian Robinson. The motion of an arbitrary rotating spherical projectile and its application to ball games. Physica Scripta 88 (2013) 018101

Antonín Štĕpánek. The aerodynamics of a tennis ball - The topspin lob. Am. J. Phys. 56 (2) February 1988, pp 138-142

Donald C. Warren. The hardest-hit home run?. Am. J. Phys. 92 (11), November 2024. pp. 834-840