Una varilla vertical penetra en el agua

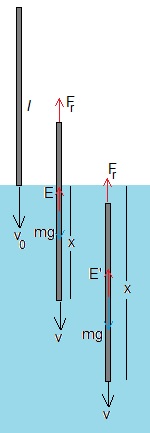
Una varilla en posición vertical de longitud l y sección S hecha de un material de densidad ρ, penetra en el agua de densidad ρ_f con velocidad inicial v₀, tal como se muestra en la figura. Supondremos que la densidad de la varilla es mayor que la del agua

Vamos a estudiar el movimiento de la varilla, suponiendo que el medio ejerce una fuerza de rozamiento proporcional a la velocidad

Las fuerzas que actúan sobre la varilla son:

El peso, mg=ρSl·g
La fuerza de rozamiento, F_r=kv, de sentido contario a la velocidad
El empuje

E=ρ_f·xS·g, cuando la varilla está parcialmente sumergida.
E'=ρ_f·lS·g, cuando la varilla está totalmente sumergida

La varilla está parcialmente sumergida x<l

Sea x la posición del extremo inferior de la varilla. Estudiamos el movimiento de la varilla parcialmente sumergida, x<l

$\begin{array}{l} m \frac{d^{2} x}{d t^{2}} = m g - (ρ_{f} S x) g - k \frac{d x}{d t} \\ \frac{d^{2} x}{d t^{2}} + \frac{k}{m} \frac{d x}{d t} + \frac{ρ_{f}}{ρ} g \frac{x}{l} = g \end{array}$

La ecuación característica tiene dos raíces reales negativas

$\begin{array}{l} r^{2} + \frac{k}{m} r + \frac{ρ_{f}}{ρ} \frac{g}{l} = 0 \\ r_{1} = \frac{- \frac{k}{m} + \sqrt{\frac{k^{2}}{m^{2}} - 4 \frac{ρ_{f}}{ρ} \frac{g}{l}}}{2}, r_{2} = \frac{- \frac{k}{m} - \sqrt{\frac{k^{2}}{m^{2}} - 4 \frac{ρ_{f}}{ρ} \frac{g}{l}}}{2} \end{array}$

La solución de la ecuación diferencial homogénea es

$x_{h} = A_{1} \exp (r_{1} t) + B_{1} \exp (r_{2} t)$

La solución particular es una cosntante C tal que

$\begin{array}{l} \frac{ρ_{f}}{ρ} g \frac{C}{l} = g \\ C = \frac{ρ}{ρ_{f}} l \end{array}$

La solución completa es la suma de las dos

$\begin{array}{l} x = A_{1} \exp (r_{1} t) + B_{1} \exp (r_{2} t) + \frac{ρ}{ρ_{f}} l \\ \frac{d x}{d t} = r_{1} A_{1} \exp (r_{1} t) + r_{2} B_{1} \exp (r_{2} t) \end{array}$

Los coeficientes A₁ y B₁ se determinan a partir de las condiciones iniciales, en el instante t=0, la posición del extremo inferior de la varilla es x=0 y su velocidad es dx/dt=v₀

$\begin{array}{l} {\begin{cases} 0 = A_{1} + B_{1} + \frac{ρ}{ρ_{f}} l \\ v_{0} = r_{1} A_{1} + r_{2} B_{1} \end{cases} \\ A_{1} = \frac{v_{0} + r_{2} \frac{ρ}{ρ_{f}} l}{r_{1} - r_{2}}, B_{1} = - \frac{v_{0} + r_{1} \frac{ρ}{ρ_{f}} l}{r_{1} - r_{2}} \end{array}$

La varilla está completamente sumergida x=l en el instante t₀, raíz de la ecuación transcendente

$\begin{array}{l} l = A_{1} \exp (r_{1} t) + B_{1} \exp (r_{2} t) + \frac{ρ}{ρ_{f}} l \\ (1 - \frac{ρ}{ρ_{f}}) l = A_{1} \exp (r_{1} t) + B_{1} \exp (r_{2} t) \end{array}$

En dicho instante la velocidad de la varilla es

$v_{01} = r_{1} A_{1} \exp (r_{1} t_{0}) + r_{2} B_{1} \exp (r_{2} t_{0})$

La varilla está completamente sumergida x>l

La ecuación del movimiento es ahora

$\begin{array}{l} m \frac{d^{2} x}{d t^{2}} = m g - (ρ_{f} S l) g - k \frac{d x}{d t} \\ \frac{d^{2} x}{d t^{2}} + \frac{k}{m} \frac{d x}{d t} = g (1 - \frac{ρ_{f}}{ρ}) \end{array}$

La ecuación característica tiene dos raíces reales

$\begin{array}{l} r^{2} + \frac{k}{m} r = 0 \\ r_{1} = 0, r_{2} = - \frac{k}{m} \end{array}$

La solución de la ecuación diferencial homogénea es

$x_{h} = A_{2} + B_{2} \exp (r_{2} (t - t_{0}))$

La solución particular ya no es una constante, sino C(t-t₀), introduciendo en la ecuación diferencial

$\begin{array}{l} \frac{k}{m} C = g (1 - \frac{ρ_{f}}{ρ}) \\ C = (1 - \frac{ρ_{f}}{ρ}) \frac{m g}{k} \end{array}$

La solución completa para t>t₀ es

$\begin{array}{l} x = A_{2} + B_{2} \exp (r_{2} (t - t_{0})) + (1 - \frac{ρ_{f}}{ρ}) \frac{m g}{k} (t - t_{0}) \\ \frac{d x}{d t} = B_{2} r_{2} \exp (r_{2} (t - t_{0})) + (1 - \frac{ρ_{f}}{ρ}) \frac{m g}{k} \end{array}$

Los coeficientes A₂ y B₂ se determinan a partir de las condiciones iniciales, en el instante t=t₀, la posición del extremo inferior de la varilla es x=l y su velocidad es dx/dt=v₀₁

$\begin{array}{l} {\begin{cases} l = A_{2} + B_{2} \\ v_{01} = B_{2} r_{2} + (1 - \frac{ρ_{f}}{ρ}) \frac{m g}{k} \end{cases} \\ B_{2} = \frac{v_{01} - (1 - \frac{ρ_{f}}{ρ}) \frac{m g}{k}}{r_{2}} =, A_{2} = l - B_{2} \end{array}$

Como la raíz r₂ es negativa, la velocidad final tiende a

$v_{\infty} = (1 - \frac{ρ_{f}}{ρ}) \frac{m g}{k}$

La velocidad final es independiente de la inicial v₀

Ejemplos

Los datos son los siguientes

Densidad del agua, ρ_f=1000 kg/m³
Densidad de la varilla, ρ=2000 kg/m³
Longitud de la varilla, l=2 m
Sección de la varilla, S=1 cm²
Fuerza de rozamiento, constante, k=1 s^-1
Velocidad inicial v₀=0, (parte del reposo), v₀=4 m/s

Representamos la velocidad de la varilla en función del tiempo, calculando el instante t₀ mediante la fzero de MATLAB y representándolo mediante una línea vertical a trazos.

k=1;
rho_f=1000; %densidad del agua
rho=2000; %densidad varilla
S=1e-4; %sección varilla
l=2; %longitud varilla
m=rho*S*l; %masa de la varilla
dis=sqrt(k^2/m^2-4*rho_f*9.8/(rho*l)); %discriminante

hold on
for v0=[0,4]
     %primera etapa
    r1=(-k/m+dis)/2; %raíces de la ecuación característica
    r2=(-k/m-dis)/2;
    A1=(v0+r2*rho*l/rho_f)/(r1-r2); %coeficientes
    B1=-(v0+r1*rho*l/rho_f)/(r1-r2);
    x=@(t) A1*exp(r1*t)+B1*exp(r2*t)+rho*l/rho_f;
    f=@(t) x(t)-l;
    t0=fzero(f,[0,10]); %instante completamente sumergida
    v=@(t) A1*r1*exp(r1*t)+B1*r2*exp(r2*t);
    v0_1=v(t0);
    
    %segunda etapa
    r2=-k/m; %raíz de la ecuación acaracterística
    B2=(v0_1-(1-rho_f/rho)*m*9.8/k)/r2; %coeficientes
    A2=l-B2;
    
    %x1=@(t) A2+B2*exp(r2*(t-t0))+(1-rho_f/rho)*m*9.8*(t-t0)/k;
    v1=@(t) B2*r2*exp(r2*(t-t0))+(1-rho_f/rho)*m*9.8/k;
    line([t0,t0],[0,v(t0)],'lineStyle','--')
    fplot(v,[0,t0])
    fplot(v1,[t0, 5])
end
hold off
grid on
xlabel('t (s)')
ylabel('v (m/s)')
title('Velocidad')

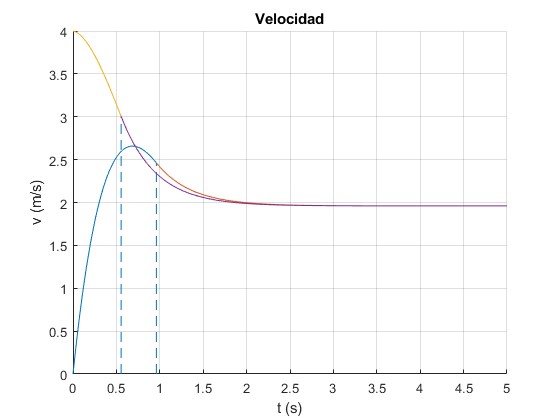
La velocidad límite constante v_∞, independiente de la velocidad inicial es

>> (1-rho_f/rho)*m*9.8/k
ans =   1.9600

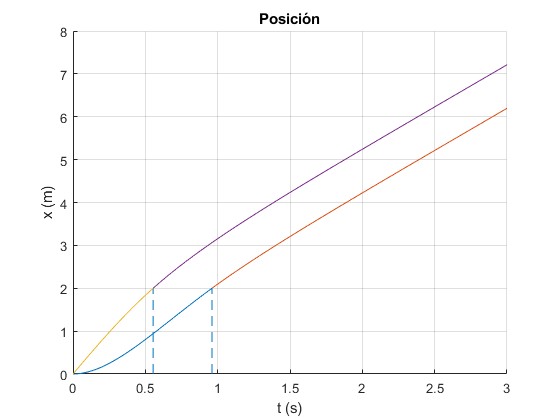
Representamos la posición x del extremo inferior de la varilla

k=1;
rho_f=1000; %densidad del agua
rho=2000; %densidad varilla
S=1e-4; %sección varilla
l=2; %longitud varilla
m=rho*S*l; %masa de la varilla
dis=sqrt(k^2/m^2-4*rho_f*9.8/(rho*l)); %discriminante
 
hold on
for v0=[0,4]
     %primera etapa
    r1=(-k/m+dis)/2; %raíces de la ecuación característica
    r2=(-k/m-dis)/2;
    A1=(v0+r2*rho*l/rho_f)/(r1-r2); %coeficientes
    B1=-(v0+r1*rho*l/rho_f)/(r1-r2);  
    x=@(t) A1*exp(r1*t)+B1*exp(r2*t)+rho*l/rho_f;
    f=@(t) x(t)-l;
    t0=fzero(f,[0,10]); %instante completamente sumergida
    v0_1=r1*A1*exp(r1*t0)+r2*B1*exp(r2*t0);
    
    %segunda etapa
    r2=-k/m; %raíz de la ecuación acaracterística
    B2=(v0_1-(1-rho_f/rho)*m*9.8/k)/r2; %coeficientes
    A2=l-B2;
    
    x1=@(t) A2+B2*exp(r2*(t-t0))+(1-rho_f/rho)*m*9.8*(t-t0)/k;
    line([t0,t0],[0,x(t0)],'lineStyle','--')
    fplot(x,[0,t0])
    fplot(x1,[t0, 3])
end
hold off
grid on
xlabel('t (s)')
ylabel('x (m)')
title('Posición')

Referencias

HANG Yu-feng, XIE Dong, WEI Xiang-zhong, SHANGGUAN Wang-zuo. Analytical calculation and numerical simulation of the dynamics of water-entry of a slender rod. College Physics. Volume 43, Issue 01, March 2024