Cuerda formada por dos segmentos

Las ecuaciones diferenciales del movimiento ondulatorio, son respectivamente

${\displaystyle v_1^2\frac{{\partial }^2{\psi }_1}{\partial x^2}=\frac{{\partial }^2{\psi }_1}{\partial t^2}{v}_2^2\frac{{\partial }^2{\psi }_2}{\partial x^2}=\frac{{\partial }^2{\psi }_2}{\partial t^2}}$

Ψ es el desplazamiento trasversal de un punto x de la cuerda en el instante t.

v₁ y v₂ son las velocidades de propagación de las ondas trasversales en las partes izquierda y derecha de la cuerda sometida a la tensión T

${\displaystyle v_1=\sqrt{\frac{T}{{\mu }_1}}{v}_2=\sqrt{\frac{T}{{\mu }_2}}}$

Siguiendo los mismos pasos que para una cuerda homogénea sujeta por ambos extremos, ensayamos la solución

Ψ(x,t)=y(x)sin(ωt)

que describe una onda estacionaria. Cada punto de la cuerda vibra con una amplitud y(x) y con frecuencia angular ω.

Introduciendo esta expresión en cada una de las dos ecuaciones diferenciales del movimiento ondulatorio, obtenemos las ecuaciones diferenciales similares a las de un M.A.S.

${\displaystyle \frac{d^2{y}_1}{d{x}^2}+\frac{{\omega }^2}{v_1^2}{y}_1=0\frac{d^2{y}_2}{d{x}^2}+\frac{{\omega }^2}{v_2^2}{y}_2=0}$

Las soluciones de estas ecuaciones diferenciales son

y₁(x)=A₁sin (k₁x)+B₁cos(k₁x) 
y₂(x)=A₂sin (k₂x)+B₂cos(k₂x) 

k₁=ω/v₁ y k₂=ω/v₂  son los números de onda, respectivos

Los coeficientes A₁, B₁, A₂ y B₂, vienen determinados por la continuidad de la función de onda en x=0 y por las condiciones de contorno en los extremos fijos x=0 y x=L.

Condiciones de contorno

El extremo izquierdo de la cuerda está sujeto en x=0 y el extremo derecho en x=L. Se tiene que cumplir que

${\displaystyle \{\begin{array}{l}{y}_1(0)=\mathrm{0,}{B}_1=0\\ y_2(L)=\mathrm{0,}{A}_2\sin (k_{2}L)+B_2\cos (k_{2}L)=0\end{array}}$

Continuidad de la función que describe la onda estacionaria

En el punto x=a, las dos mitades de la cuerda se unen. La función que describe la onda estacionaria tiene que ser continua y también su derivada primera.

${\displaystyle \begin{array}{l}{y}_1(a)=y_2(a)A_1\sin \left(k_{1}a\right)=A_2\sin \left(k_{2}a\right)+B_2\cos \left(k_{2}a\right)\hfill \\ {\frac{\partial y_1}{\partial x}|}_a={\frac{\partial y_2}{\partial x}|}_a{k}_1{A}_1\sin \left(k_{1}a\right)=k_2\left(A_2\cos \left(k_{2}a\right)-B_2\sin \left(k_{2}a\right)\right)\hfill \end{array}}$

Tenemos un sistema homogéneo de tres ecuaciones con tres incógnitas, A₁, A₂ y B₂, despejamos B₂ en la primera ecuación

${\displaystyle B_2=-A_2\frac{\sin (k_{2}L)}{\cos (k_{2}L)}}$

Sustituimos en las otras dos

${\displaystyle \{\begin{array}{l}{A}_1\sin \left(k_{1}a\right)=A_2\sin \left(k_{2}a\right)-A_2\frac{\sin (k_{2}L)}{\cos (k_{2}L)}\cos \left(k_{2}a\right)\\ k_1{A}_1\sin \left(k_{1}a\right)=k_2\left(A_2\cos \left(k_{2}a\right)+A_2\frac{\sin (k_{2}L)}{\cos (k_{2}L)}\sin \left(k_{2}a\right)\right)\end{array}}$

Utilizamos la fórmula, cos(A-B)=cosA·cosB+sinA·sinB, dividimos las dos ecuaciones

${\displaystyle \frac{1}{k_1}\frac{\sin \left(k_{1}a\right)}{\cos \left(k_{1}a\right)}=\frac{1}{k_2}\frac{\sin \left(k_2(a-L)\right)}{\cos \left(k_2(a-L)\right)}}$

Frecuencias de los modos de vibración de la cuerda

Para calcular las frecuencias de los modos de vibración de la cuerda se resuelve la ecuación trascendente en ω

${\displaystyle k_2\sin \left(k_{1}a\right)\cos \left(k_2(L-a)\right)+k_1\cos \left(k_{1}a\right)\sin \left(k_2(L-a)\right)=0}$

Llamemos r al cociente de velocidades de propagación en las porciones de cuerda, v₂=r·v₁ o bien, k₂=k₁/r

${\displaystyle \frac{k_1}{r}\sin \left(k_{1}a\right)\cos \left(\frac{k_1}{r}(L-a)\right)+k_1\cos \left(k_{1}a\right)\sin \left(\frac{k_1}{r}(L-a)\right)=0}$

Sea la longitud de la cuerda L=1 m, la proción izquierda de la cuerda tiene una longitud a=L/3. Las densidades lineales de la cuerda son tales que la relación de las velocidades de propagación entre las dos porciones de la cuerda es, v₂=2v₁

Como veremos en el ejemplo, más abajo, en este caso, no es necesario resolver la ecuación transcendente por procedimientos numéricos.

function cuerda3
    L=1; %longitud de la cuerda
    a=L/3;  %porción izquierda
    r=2; %v2=r·v1, k2=k1/r
    f=@(x) x.*sin(a*x).*cos((L-a)*x/r)/r+x.*cos(a*x).*sin(x*(L-a)/r);
    fplot(f,[0,20]);
    grid on
    xlabel('x')
    ylabel('f(x)')
    title('Raíces')
    
    x=linspace(1,20,20);
    disp('frecuencias (Hz)')
    raiz=raices(f,x);
    disp(raiz/(2*pi))

    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
    end
end

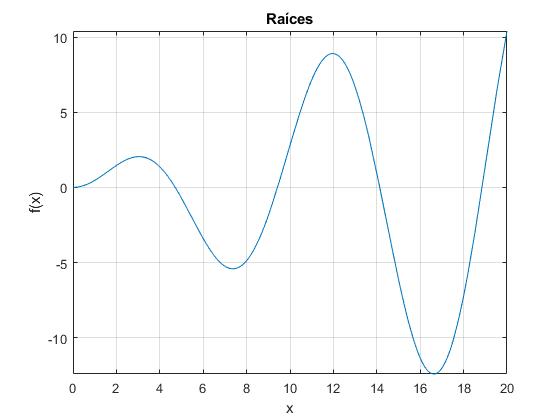
Las frecuencias ω=v₁k₁, f=ω/2π de los primeros modos de vibración son

frecuencias (Hz)
    0.7500    1.5000    2.2500    3.0000

Amplitudes de los modos de vibración

Despejamos A₂ y B₂ en función de A₁, tomando las dos primeras ecuaciones del sistema homogéneo de tres ecuaciones con tres incógnitas

${\displaystyle \begin{array}{l}{A}_2=-A_1\cos (k_{2}L)\frac{\sin (k_{1}a)}{\sin \left(k_2(L-a)\right)}\hfill \\ B_2=-A_2\frac{\sin (k_{2}L)}{\cos (k_{2}L)}=A_1\sin (k_{2}L)\frac{\sin (k_{1}a)}{\sin \left(k_2(L-a)\right)}\hfill \end{array}}$

Puede ocurrir una indeterminación 0/0, cuando k₁a=nπ y a la vez, k₂(L-a)=mπ. La indeterminación se resuelve aplicando la regla de de L'Hôpital tal como veremos en el ejemplo.

${\displaystyle \begin{array}{l}{A}_2=A_1\cos (k_{2}L)\underset{x\to a}{\lim }\frac{\sin (k_{1}x)}{\sin (k_2(x-L))}=A_1\cos (k_{2}L)\frac{k_1}{k_2}\frac{\cos (k_{1}a)}{\cos \left(k_2(L-a)\right)}\hfill \\ B_2=-A_1\sin (k_{2}L)\frac{k_1}{k_2}\frac{\cos (k_{1}a)}{\cos \left(k_2(L-a)\right)}\hfill \end{array}}$

Para el modo de vibración de frecuencia angular ω=2πf, con k₁=ω/v₁ y k₂=ω/v₂

${\displaystyle \{\begin{array}{l}{y}_1(x)=A_1\sin \left(k_{1}x\right),0\le x<a\\ y_2(x)=A_2\sin \left(k_{2}x\right)+B_2\cos \left(k_{2}x\right),a\le x<L\end{array}}$

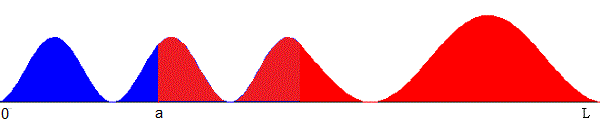
A₁ es un factor de escala. Para que todos los modos de vibración se representen a la misma escala, se calcula A₁ haciendo que el área bajo la curva del cuadrado de la amplitud y(x) multiplicada por la densidad en cada tramo sea la unidad

${\displaystyle \begin{array}{l}{\mu }_1{\displaystyle \underset{0}{\overset{a}{\int }}{y}_1^2(x)dx}+{\mu }_2{\displaystyle \underset{a}{\overset{L}{\int }}{y}_2^2(x)dx}=1\\ {\mu }_1{\displaystyle \underset{0}{\overset{a}{\int }}{A}_1^2{\sin }^2(k_{1}x)dx}+{\mu }_2{\displaystyle \underset{a}{\overset{L}{\int }}{\left(A_2\sin (k_{2}x)+B_2\cos (k_{2}x)\right)}^{2}dx}=1\end{array}}$

La integral definida de la izquierda es el área sombreada en color azul y la integral de la derecha es el área sombreada en color rojo.

Relaciones de ortogonalidad

Las relaciones de ortogonalidad de Φ_n(x) para una cuerda no homogénea de densidad μ(x)

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{L}{\int }}\mu (x){\Phi }_m(x){\Phi }_n(x)dx}=\mathrm{0,}m\ne n\\ {\mu }_1{\displaystyle \underset{0}{\overset{a}{\int }}{y}_{1m}(x)y_{1n}(x)dx}+{\mu }_2{\displaystyle \underset{a}{\overset{L}{\int }}{y}_{2m}(x)y_{2n}(x)dx=\mathrm{0,}}m\ne n\end{array}}$

m y n son dos los modos de vibración distintos. Véase el ejemplo más abajo

Ejemplo

Sea una cuerda no homogénea, de longitud L=1 m. La parte izquierda a=L/3, de densidad μ₁=4μ, la parte derecha de longitud L-a=2L/3 de densidad lineal μ₂=μ

La velocidad de propagación de las ondas trasnversales en las cuerdas son

${\displaystyle \begin{array}{l}{v}_1=\sqrt{\frac{T}{{\mu }_1}}=\sqrt{\frac{T}{4\mu }}{v}_2=\sqrt{\frac{T}{{\mu }_2}}=\sqrt{\frac{T}{\mu }}\\ v_2=2v_1\\ k_1=\frac{\omega }{v_1},k_2=\frac{\omega }{v_2}=\frac{k_1}{2}\end{array}}$

Frecuencias de los modos de vibración

${\displaystyle \begin{array}{l}\frac{k_1}{2}\sin \left(k_1\frac{L}{3}\right)\cos \left(\frac{k_1}{2}\frac{2L}{3}\right)+k_1\cos \left(k_1\frac{L}{3}\right)\sin \left(\frac{k_1}{2}\frac{2L}{3}\right)=0\\ \frac{3}{2}{k}_1\sin \left(k_1\frac{L}{3}\right)\cos \left(k_1\frac{L}{3}\right)=0\\ \frac{3}{4}{k}_1\sin \left(2k_1\frac{L}{3}\right)=0\\ k_{1}L=\frac{3n\pi }{2}\\ {\omega }_n=n\pi \frac{3v_1}{2L},n=\mathrm{1,2,3...}\end{array}}$

Amplitudes

• ${\displaystyle n=\mathrm{1,}{k}_1=\frac{3\pi }{2L},k_2=\frac{3\pi }{4L}}$

${\displaystyle \begin{array}{l}{A}_2=A_1\frac{\sin \left(\frac{3\pi }{2L}\frac{L}{3}\right)\cos \left(\frac{3\pi }{4L}L\right)}{\sin \left(-\frac{3\pi }{4L}\frac{2L}{3}\right)}=\frac{\sqrt{2}}{2}{A}_1\\ B_2=-A_1\frac{\sin \left(\frac{3\pi }{4L}L\right)\sin \left(\frac{3\pi }{2L}\frac{L}{3}\right)}{\sin \left(-\frac{3\pi }{4L}\frac{2L}{3}\right)}=\frac{\sqrt{2}}{2}{A}_1\end{array}}$

• ${\displaystyle n=\mathrm{2,}{k}_1=\frac{6\pi }{2L}=\frac{3\pi }{L},k_2=\frac{3\pi }{2L}}$

Indeterminación 0/0

${\displaystyle \begin{array}{l}{B}_2=-A_1\sin \left(\frac{3\pi }{2L}L\right)\underset{a\to \frac{L}{3}}{\lim }\frac{\sin \left(\frac{3\pi }{L}a\right)}{\sin \left(\frac{3\pi }{2L}(a-L)\right)}=A_1\frac{\frac{3\pi }{L}\cos \left(\frac{3\pi }{L}\frac{L}{3}\right)}{\frac{3\pi }{2L}\cos \left(\frac{3\pi }{2L}\left(\frac{L}{3}-L\right)\right)}=2A_1\\ A_2=A_1\frac{\sin \left(\frac{3\pi }{L}\frac{L}{3}\right)\cos \left(\frac{3\pi }{2L}L\right)}{\sin \left(-\frac{3\pi }{2L}\frac{2L}{3}\right)}=0\end{array}}$

• ${\displaystyle n=\mathrm{3,}{k}_1=\frac{9\pi }{2L},k_2=\frac{9\pi }{4L}}$

${\displaystyle \begin{array}{l}{A}_2=A_1\frac{\sin \left(\frac{9\pi }{2L}\frac{L}{3}\right)\cos \left(\frac{9\pi }{4L}L\right)}{\sin \left(-\frac{9\pi }{4L}\frac{2L}{3}\right)}=-\frac{\sqrt{2}}{2}{A}_1\\ B_2=-A_1\frac{\sin \left(\frac{9\pi }{4L}L\right)\sin \left(\frac{9\pi }{2L}\frac{L}{3}\right)}{\sin \left(-\frac{9\pi }{4L}\frac{2L}{3}\right)}=\frac{\sqrt{2}}{2}{A}_1\end{array}}$

• ${\displaystyle n=\mathrm{4,}{k}_1=\frac{6\pi }{L},k_2=\frac{3\pi }{L}}$

Indeterminación 0/0

${\displaystyle \begin{array}{l}{A}_2=A_1\cos \left(\frac{3\pi }{L}L\right)\underset{a\to \frac{L}{3}}{\lim }\frac{\sin \left(\frac{6\pi }{L}a\right)}{\sin \left(\frac{3\pi }{L}(a-L)\right)}=-2A_1\\ B_2=-A_1\frac{\sin \left(\frac{3\pi }{L}L\right)\sin \left(\frac{6\pi }{L}\frac{L}{3}\right)}{\sin \left(-\frac{3\pi }{L}\frac{2L}{3}\right)}=0\end{array}}$

Comprobamos las relaciones de ortogonalidad, sea m=1 y n=2

L=1;
a=L/3;
mu=4; %densidad parte izquierda, mu=1, derecha
k1=3*pi/(2*L);  %modo de vibración n=1
k2=k1/sqrt(mu);
a2=-cos(k2*L)*sin(k1*a)/sin(k2*(L-a));
b2=sin(k2*L)*sin(k1*a)/sin(k2*(L-a));
y1=@(x) sin(k1*x);
y2=@(x) a2*sin(k2*x)+b2*cos(k2*x);

K1=6*pi/(2*L);  %modo de vibración n=2; 
K2=K1/2;
Y1=@(x) sin(K1*x);
A2=cos(K2*L)*K1*cos(K1*a)/(K2*cos(K2*(L-a)));
B2=-sin(K2*L)*K1*cos(K1*a)/(K2*cos(K2*(L-a)));
Y2=@(x) A2*sin(K2*x)+B2*cos(K2*x);

z1=@(x) y1(x).*Y1(x);
z2=@(x) y2(x).*Y2(x);
res=mu*integral(z1,0,a)+integral(z2,a,L);
disp(res)

Comprobamos las relaciones de ortogonalidad, la integral vale cero. Los coeficientes son los que hemos obtenido con n=1 y n=2

    0
>> a2,b2
a2 =    0.7071
b2 =    0.7071
>> A2,B2
A2 =  -3.6739e-16
B2 =     2 

Representamos los primeros modos de vibración

L=1; %longitud de la cuerda
a=L/3; %porción izquierda
mu=4; %densidad parte izquierda, mu=1, derecha
hold on
for n=1:4
    k1=3*n*pi/(2*L); 
    k2=k1/sqrt(mu); %Relación de velocidades de propagación, v2=2*v1
    A2=-sin(k1*a)*cos(k2*L)/sin(k2*(L-a));
    B2=sin(k2*L)*sin(k1*a)/sin(k2*(L-a));
    if mod(k1*a/pi,1)<1e-6 && mod(k2*(L-a)/pi,1)<1e-6 %indeterminación 0/0
        A2=k1*cos(k2*L)*cos(k1*a)/(k2*cos(k2*(L-a)));
        B2=-k1*sin(k2*L)*cos(k1*a)/(k2*cos(k2*(L-a)));
    end
    y1=@(x) sin(k1*x);
    y2=@(x) A2*sin(k2*x)+B2*cos(k2*x);
    z1=@(x) y1(x).^2;
    z2=@(x) y2(x).^2;
    area=mu*integral(z1,0,a)+integral(z2,a,L);
    A1=1/sqrt(area);
    f=@(x) A1*(x<a).*y1(x)+(x>=a).*y2(x)*A1;
    fplot(f,[0,L],'displayName',num2str(k1/(2*pi)))
end
hold off
grid on
legend('-DynamicLegend','location','southwest')
xlabel('x')
ylabel('y')
title('Modos de vibración')

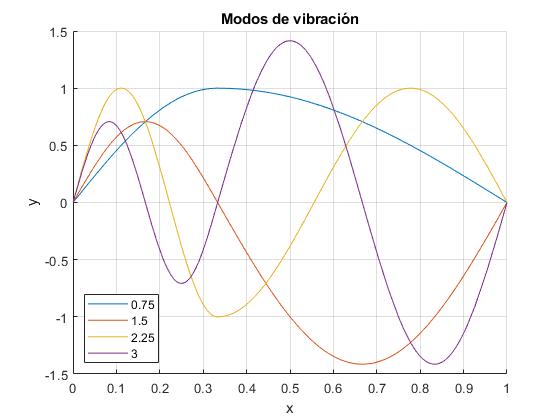
Cambiamos el valor de a=L/2. Resolvemos la ecuación transcendente para calcular las frecuencias de los primeros modos de vibración.

function cuerda4
    L=1; %longitud de la cuerda
    a=L/2; %porción izquierda
    mu=4; %densidad parte izquierda, mu=1, derecha
    r=sqrt(mu); %v2=r·v1, k2=k1/r
    %raices, k1
    f=@(x) x.*sin(a*x).*cos((L-a)*x/r)/r+x.*cos(a*x).*sin(x*(L-a)/r);
    x=linspace(1,15,20);
    raiz=raices(f,x);
    
    hold on
    for n=1:length(raiz)
        k1=raiz(n);
        k2=k1/r;
        A2=sin(k1*a)*cos(k2*L)/sin(k2*(a-L));
        B2=-sin(k2*L)*sin(k1*a)/sin(k2*(a-L));
        if mod(k1*a/pi,1)<1e-6 && mod(k2*(L-a)/pi,1)<1e-6 %indeterminación 0/0
            A2=k1*cos(k2*L)*cos(k1*a)/(k2*cos(k2*(a-L)));
            B2=-k1*sin(k2*L)*cos(k1*a)/(k2*cos(k2*(a-L)));
        end
        y1=@(x) sin(k1*x);
        y2=@(x) A2*sin(k2*x)+B2*cos(k2*x);
        z1=@(x) y1(x).^2;
        z2=@(x) y2(x).^2;
        area=mu*integral(z1,0,a)+integral(z2,a,L);
        A1=1/sqrt(area);
        f=@(x) A1*(x<a).*y1(x)+(x>=a).*y2(x)*A1;
        fplot(f,[0,L],'displayName',num2str(k1/(2*pi)))
    end
    hold off
    grid on
    legend('-DynamicLegend','location','southwest')
    xlabel('x')
    ylabel('y')
    title('Modos de vibración')

    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
    end
end

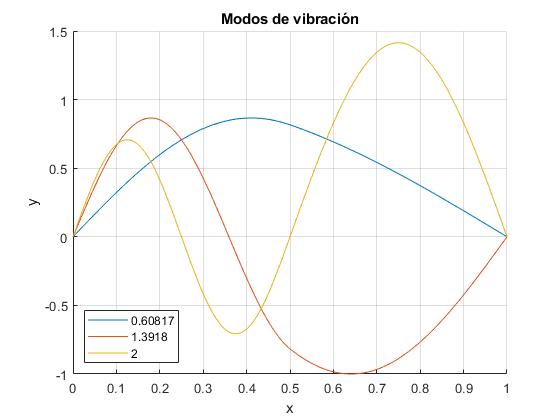
Comprobamos la relación de ortogonalidad con n=1 y m=2.

L=1; %longitud de la cuerda
a=L/2; %porción izquierda
mu=4; %densidad parte izquierda, mu=1, derecha
r=sqrt(mu); %v2=r·v1, k2=k1/r
%raices, k1
f=@(x) x.*sin(a*x).*cos((L-a)*x/r)/r+x.*cos(a*x).*sin(x*(L-a)/r);
x=linspace(1,40,20);
raiz=raices(f,x);

k1=raiz(1);  %modo de vibración n=1
k2=k1/r;
a2=-cos(k2*L)*sin(k1*a)/sin(k2*(L-a));
b2=sin(k2*L)*sin(k1*a)/sin(k2*(L-a));
y1=@(x) sin(k1*x);
y2=@(x) a2*sin(k2*x)+b2*cos(k2*x);

K1=raiz(2);  %modo de vibración n=2; 
K2=K1/r;
Y1=@(x) sin(K1*x);
A2=-cos(K2*L)*sin(K1*a)/sin(K2*(L-a));
B2=sin(K2*L)*sin(K1*a)/sin(K2*(L-a));

%A2=cos(K2*L)*K1*cos(K1*a)/(K2*cos(K2*(L-a))); %para n=3, 6, ...
%B2=-sin(K2*L)*K1*cos(K1*a)/(K2*cos(K2*(L-a)));
Y2=@(x) A2*sin(K2*x)+B2*cos(K2*x);

z1=@(x) y1(x).*Y1(x);
z2=@(x) y2(x).*Y2(x);
res=mu*integral(z1,0,a)+integral(z2,a,L);
disp(res)

   1.1102e-16

En este caso, a=L/2, para n=3, 6, 9... hay que utilizar las amplitudes obtenidas aplicando la regla de L'Hôpital (para resolver la indeterminación 0/0)

Cuerda formada por tres segmentos

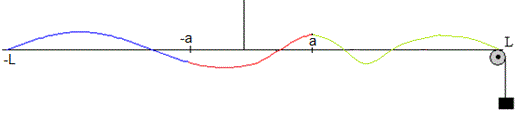
Estudiamos los modos de vibración producidas en una cuerda no homogénea sujeta por ambos extremos. La cuerda de longitud 2L está formada por tres partes una de longitud L-a, otra de longitud 2a y otra de longitud L-a de distinta densidad lineal μ₁, μ₂, y μ₃, respectivamente. Las ecuaciones diferenciales del movimiento ondulatorio, son respectivamente

${\displaystyle v_1^2\frac{{\partial }^2{\psi }_1}{\partial x^2}=\frac{{\partial }^2{\psi }_1}{\partial t^2},v_2^2\frac{{\partial }^2{\psi }_2}{\partial x^2}=\frac{{\partial }^2{\psi }_2}{\partial t^2} ,v_3^2\frac{{\partial }^2{\psi }_3}{\partial x^2}=\frac{{\partial }^2{\psi }_3}{\partial t^2}}$

v₁, v₂ y v₃ son las velocidades de propagación de las ondas trasversales en las tres partes de la cuerda cuya tensión es T

${\displaystyle v_1=\sqrt{\frac{T}{{\mu }_1}},v_2=\sqrt{\frac{T}{{\mu }_2}},v_3=\sqrt{\frac{T}{{\mu }_3}}}$

Siguiendo los mismos pasos que para una cuerda homogénea sujeta por ambos extremos, ensayamos la solución

Ψ(x,t)=y(x)sin(ωt)

que describe una onda estacionaria. Cada punto de la cuerda vibra con una amplitud y(x) y con frecuencia angular ω.

Introduciendo esta expresión en cada una de las tres ecuaciones diferenciales del movimiento ondulatorio, obtenemos las ecuaciones diferenciales similares a las de un M.A.S.

${\displaystyle \frac{d^2{y}_1}{d{x}^2}+\frac{{\omega }^2}{v_1^2}{y}_1=\mathrm{0,}\frac{d^2{y}_2}{d{x}^2}+\frac{{\omega }^2}{v_2^2}{y}_2=\mathrm{0,}\frac{d^2{y}_3}{d{x}^2}+\frac{{\omega }^2}{v_2^2}{y}_3=0}$

Las soluciones de estas ecuaciones diferenciales son la parte real de

${\displaystyle \{\begin{array}{l}{y}_1(x)=A_1\exp \left(i{k}_{1}x\right)+B_1\exp \left(-i{k}_{1}x\right),k_1=\frac{\omega }{v_1}\\ y_2(x)=A_2\exp \left(i{k}_{2}x\right)+B_2\exp \left(-i{k}_{2}x\right),k_2=\frac{\omega }{v_2}\\ y_3(x)=A_3\exp \left(i{k}_{3}x\right)+B_3\exp \left(-i{k}_{3}x\right),k_3=\frac{\omega }{v_3}\end{array}}$

Los coeficientes A₁, B₁, A₂, B₂, A₃ y B₃ vienen determinados por la continuidad de la función de onda en x=-a, x=a y por las condiciones de contorno en los extremos fijos x=-L y x=L.

Continuidad de la función que describe la onda estacionaria

En x=-a y x=a, la función que describe la onda estacionaria tiene que ser continua y también su derivada primera.

${\displaystyle \begin{array}{l}x=-a,\{\begin{array}{l}{y}_1(-a)=y_1(-a)\\ A_1\exp \left(-i{k}_{1}a\right)+B_1\exp \left(i{k}_{1}a\right)=A_2\exp \left(-i{k}_{2}a\right)+B_2\exp \left(i{k}_{2}a\right)\\ {\frac{d{y}_1}{dx}|}_{x=-a}={\frac{d{y}_2}{dx}|}_{x=-a}\\ i{k}_1\left(A_1\exp \left(-i{k}_{1}a\right)-B_1\exp \left(i{k}_{1}a\right)\right)=i{k}_2\left(A_2\exp \left(-i{k}_{2}a\right)-B_2\exp \left(i{k}_{2}a\right)\right)\end{array}\\ x=a,\{\begin{array}{l}{y}_2(a)=y_3(a)\\ A_2\exp \left(i{k}_{2}a\right)+B_2\exp \left(-i{k}_{2}a\right)=A_3\exp \left(i{k}_{3}a\right)+B_3\exp \left(-i{k}_{3}a\right)\\ {\frac{d{y}_2}{dx}|}_{x=a}={\frac{d{y}_3}{dx}|}_{x=a}\\ i{k}_2\left(A_2\exp \left(i{k}_{2}a\right)-B_2\exp \left(-i{k}_{2}a\right)\right)=i{k}_3\left(A_3\exp \left(i{k}_{3}a\right)-B_3\exp \left(-i{k}_{3}a\right)\right)\end{array}\end{array}}$

En forma matricial

${\displaystyle \begin{array}{l}\left(\begin{array}{cc}{e}^{-i{k}_{1}a}& e^{i{k}_{1}a}\\ k_1{e}^{-i{k}_{1}a}& -k_1{e}^{i{k}_{1}a}\end{array}\right)\left(\begin{array}{c}{A}_1\\ B_1\end{array}\right)=\left(\begin{array}{cc}{e}^{-i{k}_{2}a}& e^{i{k}_{2}a}\\ k_2{e}^{-i{k}_{2}a}& -k_2{e}^{i{k}_{2}a}\end{array}\right)\left(\begin{array}{c}{A}_2\\ B_2\end{array}\right)\\ \left(\begin{array}{cc}{e}^{i{k}_{2}a}& e^{-i{k}_{2}a}\\ k_2{e}^{i{k}_{2}a}& -k_2{e}^{-i{k}_{2}a}\end{array}\right)\left(\begin{array}{c}{A}_2\\ B_2\end{array}\right)=\left(\begin{array}{cc}{e}^{i{k}_{3}a}& e{-}^{i{k}_{3}a}\\ k_3{e}^{i{k}_{3}a}& -k_3{e}^{-i{k}_{3}a}\end{array}\right)\left(\begin{array}{c}{A}_3\\ B_3\end{array}\right)\end{array}}$

Relacionamos los coeficientes A₁, B₁, con A₃ y B₃

${\displaystyle \begin{array}{l}{M}_{k_1,-a}\left(\begin{array}{c}{A}_1\\ B_1\end{array}\right)=M_{k_2,-a}\left(\begin{array}{c}{A}_2\\ B_2\end{array}\right),\left(\begin{array}{c}{A}_2\\ B_2\end{array}\right)=M_{k_2,-a}^{-1}{M}_{k_1,-a}\left(\begin{array}{c}{A}_1\\ B_1\end{array}\right)\\ M_{k_2,a}\left(\begin{array}{c}{A}_2\\ B_2\end{array}\right)=M_{k_3,a}\left(\begin{array}{c}{A}_3\\ B_3\end{array}\right),\\ \left(\begin{array}{c}{A}_3\\ B_3\end{array}\right)=M_{k_3,a}^{-1}{M}_{k_2,a}\left(\begin{array}{c}{A}_2\\ B_2\end{array}\right)=M_{k_3,a}^{-1}{M}_{k_2,a}{M}_{k_2,-a}^{-1}{M}_{k_1,-a}\left(\begin{array}{c}{A}_1\\ B_1\end{array}\right)\end{array}}$

Matriz inversa de una matriz 2×2

${\displaystyle \begin{array}{l}{\left(\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right)}^{-1}=\frac{1}{\left|\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right|}\left(\begin{array}{cc}{a}_{22}& -a_{12}\\ -a_{21}& a_{11}\end{array}\right)\\ M_k^{-1}={\left(\begin{array}{cc}{e}^{ikx}& e^{-ikx}\\ k{e}^{ikx}& -k{e}^{-ikx}\end{array}\right)}^{-1}=\frac{1}{-2k}\left(\begin{array}{cc}-k{e}^{-ikx}& -e^{-ikx}\\ -k{e}^{ikx}& e^{ikx}\end{array}\right)=\frac{1}{2k}\left(\begin{array}{cc}k{e}^{-ikx}& e^{-ikx}\\ k{e}^{ikx}& -e^{ikx}\end{array}\right)\end{array}}$

Condiciones de contorno

El extremo izquierdo x=-L de la cuerda está sujeto y el extremo derecho x=-L, también. Se tiene que cumplir que

${\displaystyle \{\begin{array}{l}{y}_1(-L)=A_1\exp \left(-i{k}_{1}L\right)+B_1\exp \left(i{k}_{1}L\right)=\mathrm{0,}{A}_1=-B_1\exp \left(2i{k}_{1}L\right)\\ y_3(L)=A_3\exp \left(i{k}_{3}L\right)+B_3\exp \left(-i{k}_{3}L\right)=\mathrm{0,}{B}_3=-A_3\exp \left(2i{k}_{3}L\right)\end{array}}$

Las frecuencias de los modos de vibración se obtienen

${\displaystyle \begin{array}{l}\left(\begin{array}{c}{A}_3\\ B_3\end{array}\right)=\left(\begin{array}{cc}{m}_{11}& m_{12}\\ m_{21}& m_{22}\end{array}\right)\left(\begin{array}{c}{A}_1\\ B_1\end{array}\right),m=M_{k_3,a}^{-1}{M}_{k_2,a}{M}_{k_2,-a}^{-1}{M}_{k_1,-a}\\ \left(\begin{array}{c}{A}_3\\ -A_3\exp \left(2i{k}_{3}L\right)\end{array}\right)=\left(\begin{array}{cc}{m}_{11}& m_{12}\\ m_{21}& m_{22}\end{array}\right)\left(\begin{array}{c}-B_1\exp \left(2i{k}_{1}L\right)\\ B_1\end{array}\right)\\ \{\begin{array}{l}{A}_3=-m_{11}{B}_1{e}^{2i{k}_{1}L}+m_{12}{B}_1\\ -A_3{e}^{2i{k}_{3}L}=-m_{21}{B}_1{e}^{2i{k}_{1}L}+m_{22}{B}_1\end{array}\\ -\left(-m_{11}{B}_1{e}^{2i{k}_{1}L}+m_{12}{B}_1\right)e^{2i{k}_{3}L}=-m_{21}{B}_1{e}^{2i{k}_{1}L}+m_{22}{B}_1\\ m_{11}{e}^{2i(k_1+k_3)L}-m_{12}{e}^{2i{k}_{3}L}+m_{21}{e}^{2i{k}_{1}L}-m_{22}=0\end{array}}$

Frecuencias de los modos de vibración

Las frecuencias ω de los modos de vibración son aquellas que hacen que la parte real e imaginaria de la expresión

${\displaystyle m_{11}{e}^{2i(k_1+k_3)L}-m_{12}{e}^{2i{k}_{3}L}+m_{21}{e}^{2i{k}_{1}L}-m_{22}=0}$

sean nulas simultáneamente

Sea una cuerda hecha de tres segmentos cuyas velocidades de propagación son v₁=1, v₂=2, v₃=1, respectivamente la mitad de la longitud de la cuerda es L=3 y a=1. Representamos la parte real e imaginaria de dicha expresión en el intervalo de frecuencias ω de 0.5 a 2 y marcamos sus intersecciones en el ej X

function cuerda
    v1=1; %velocidades de propagación
    v2=2;
    v3=1;
    a=1;
    L=3;
    %matriz
    f=@(k,x) [exp(1i*k*x), exp(-1i*k*x); k*exp(1i*k*x), -k*exp(-1i*k*x)];
    %matriz inversa
    g=@(k,x) [k*exp(-1i*k*x), exp(-1i*k*x); k*exp(1i*k*x), -exp(1i*k*x)]/(2*k);
    hold on
    fplot(@frecuencias_r,[0.5,2])
    fplot(@frecuencias_i,[0.5,2])
    hold off
    grid on
    xlabel('\omega')
    ylabel('f(\omega)')
    title('Parte real e imaginaria')
  
  function res=frecuencias_r(w) 
        m=g(w/v3,a)*f(w/v2,a)*g(w/v2,-a)*f(w/v1,-a);
        temp=m(1,1)*exp(2*1i*(1/v1+1/v3)*w*L)-m(1,2)*exp(2*1i*w*L/v3)+
m(2,1)*exp(2*1i*w*L/v1)-m(2,2);
        res=real(temp);
    end
    function res=frecuencias_i(w) 
        m=g(w/v3,a)*f(w/v2,a)*g(w/v2,-a)*f(w/v1,-a);
        temp=m(1,1)*exp(2*1i*(1/v1+1/v3)*w*L)-m(1,2)*exp(2*1i*w*L/v3)+
m(2,1)*exp(2*1i*w*L/v1)-m(2,2);
        res=imag(temp);
    end
  end

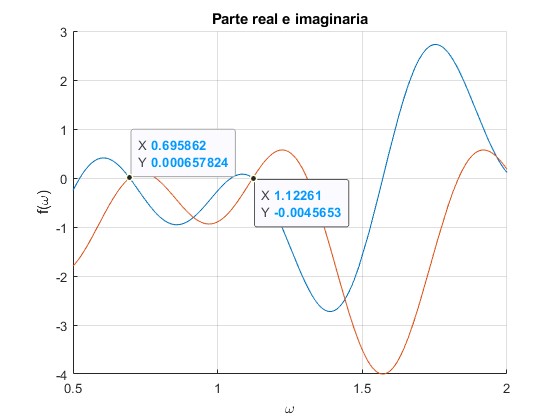
Los ceros de la parte real e imaginaria coinciden para las frecuencias ω=0.69 y 1.22, aproximadamente

Utilizamos la función fzero de MATLAB para calcularlas en el intervalo en el que la función cambia de signo

function cuerda1
    v1=1; %velocidades de propagación
    v2=2;
    v3=1;
    a=1;
    L=3;
     %matriz
    f=@(k,x) [exp(1i*k*x), exp(-1i*k*x); k*exp(1i*k*x), -k*exp(-1i*k*x)];
    %matriz inversa
    g=@(k,x) [k*exp(-1i*k*x), exp(-1i*k*x); k*exp(1i*k*x), -exp(1i*k*x)]/(2*k);
    
    %raíces
    xb=buscar_intervalos(@frecuencias_r,0.5,4, 40);
    nb=size(xb);
    for s=1:nb(1)
        frec_r(s)=fzero(@frecuencias_r,[xb(s,1) xb(s,2)]);
    end
    disp(frec_r) 
    xb=buscar_intervalos(@frecuencias_i,0.5,4, 40);
    nb=size(xb);
    for s=1:nb(1)
        frec_i(s)=fzero(@frecuencias_i,[xb(s,1) xb(s,2)]);
    end
    disp(frec_i)

    function res=frecuencias_r(w) 
        m=g(w/v3,a)*f(w/v2,a)*g(w/v2,-a)*f(w/v1,-a);
        temp=m(1,1)*exp(2*1i*(1/v1+1/v3)*w*L)-m(1,2)*exp(2*1i*w*L/v3)
+m(2,1)*exp(2*1i*w*L/v1)-m(2,2);
        res=real(temp);
    end
    function res=frecuencias_i(w) 
        m=g(w/v3,a)*f(w/v2,a)*g(w/v2,-a)*f(w/v1,-a);
        temp=m(1,1)*exp(2*1i*(1/v1+1/v3)*w*L)-m(1,2)*exp(2*1i*w*L/v3)
+m(2,1)*exp(2*1i*w*L/v1)-m(2,2);
        res=imag(temp);
    end
    
    function xb = buscar_intervalos(f,a,b,n)
        x = a:(b-a)/n:b;
        j = 0; 
        y1=f(x(1));
        xb=[];
        for i = 1:length(x)-1
            y2=f(x(i+1));
            if sign(y1) ~= sign(y2) 
                j = j + 1;
                xb(j,1) = x(i);
                xb(j,2) = x(i+1);
            end
            y1=y2;
        end
        if isempty(xb) 
            disp('no se han encontrado cambios de signo')
        else
            disp(['número de intervalos:' int2str(j)]) 
        end
    end
end

número de intervalos:11
0.5236  0.6957  1.0472  1.1216  1.5708  2.0200  2.0944  2.4459  2.6180  
3.6652  3.8373
número de intervalos:13
0.6957  0.7854  1.1216  1.3090  1.8326  2.0200  2.3562  2.4459   2.8798  3.1416  
3.4034  3.8373  3.9270

Coinciden las frecuencias, ω=0.6957, 1.1216, 2.0200, 2.4459, 3.8373

Amplitud de la onda estacionaria

Representamos la amplitud de la onda estacionaria y₁(x) en el intervalo (-L,-a), y₂(x) en el intervalo (-a,-a), e y₃(x) en el intervalo (-a, L)

${\displaystyle \{\begin{array}{l}{y}_1(x)=A_1\exp \left(i{k}_{1}x\right)+B_1\exp \left(-i{k}_{1}x\right),k_1=\frac{\omega }{v_1}\\ y_2(x)=A_2\exp \left(i{k}_{2}x\right)+B_2\exp \left(-i{k}_{2}x\right),k_2=\frac{\omega }{v_2}\\ y_3(x)=A_3\exp \left(i{k}_{3}x\right)+B_3\exp \left(-i{k}_{3}x\right),k_3=\frac{\omega }{v_3}\end{array}}$

Asignamos A₃=1. Calculamos los coeficientes A₁, B₁, A₂, B₂

${\displaystyle \begin{array}{l}\left(\begin{array}{c}{A}_2\\ B_2\end{array}\right)=M_{{}_{k_2,a}}^{-1}{M}_{k_3,a}\left(\begin{array}{c}{A}_3\\ B_3\end{array}\right),B_3=-A_3\exp \left(2i{k}_{3}L\right)\\ \left(\begin{array}{c}{A}_1\\ B_1\end{array}\right)=M_{{}_{k_1,-a}}^{-1}{M}_{k_2,-a}\left(\begin{array}{c}{A}_2\\ B_2\end{array}\right)\end{array}}$

Para que todos los modos de vibración se representen a la misma escala, se calcula A₃ haciendo que el área bajo la curva del cuadrado de la amplitud y(x) multiplicada por la densidad en cada tramo sea la unidad

${\displaystyle \begin{array}{l}{\mu }_1{\displaystyle \underset{-L}{\overset{-a}{\int }}{\left|y_1(x)\right|}^{2}dx}+{\mu }_2{\displaystyle \underset{-a}{\overset{-a}{\int }}{\left|y_2(x)\right|}^{2}dx}+{\mu }_3{\displaystyle \underset{a}{\overset{L}{\int }}{\left|y_3(x)\right|}^{2}dx}=\mathrm{1,}v=\sqrt{\frac{T}{\mu }}\\ \frac{1}{v_1^2}{\displaystyle \underset{-L}{\overset{-a}{\int }}{\left|y_1(x)\right|}^{2}dx}+\frac{1}{v_2^2}{\displaystyle \underset{-a}{\overset{-a}{\int }}{\left|y_2(x)\right|}^{2}dx}+\frac{1}{v_3^2}{\displaystyle \underset{a}{\overset{L}{\int }}{\left|y_3(x)\right|}^{2}dx}=1\end{array}}$

La integral de cada tramo se calcula de la siguiente forma

${\displaystyle \begin{array}{l}{\displaystyle \underset{x_1}{\overset{x_2}{\int }}\left(A{e}^{ikx}+B{e}^{-ikx}\right)}\left(A^{*}{e}^{-ikx}+B^{*}{e}^{ikx}\right)dx={\displaystyle \underset{x_1}{\overset{x_2}{\int }}\left(A{A}^{*}+B{B}^{*}+A{B}^{*}{e}^{2ikx}+A^{*}B{e}^{-2ikx}\right)}dx=\\ \left(A{A}^{*}+B{B}^{*}\right)\left(x_2-x_1\right)+\frac{1}{2ik}\left(A{B}^{*}\left(e^{2ik{x}_2}-e^{2ik{x}_1}\right)-A^{*}B\left(e^{-2ik{x}_2}-e^{-2ik{x}_1}\right)\right)\end{array}}$

donde el símbolo *, indica complejo conjugado

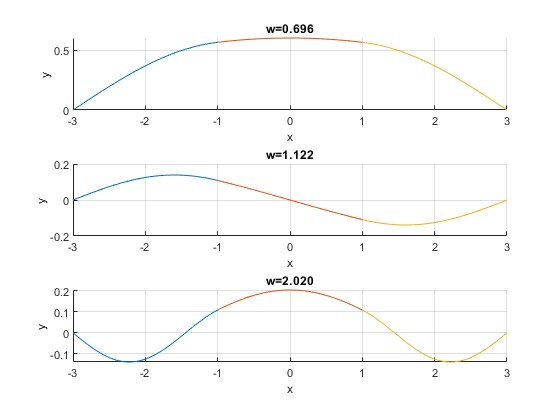
Representamos la amplitud de la onda estacionaria y(x) para las tres primeras frecuencias, ω=0.6957, 1.1216, 2.0200

function cuerda2
    v1=1; %velocidades de propagación
    v2=2;
    v3=1;
    a=1;
    L=3;
    %matriz
    f=@(k,x) [exp(1i*k*x), exp(-1i*k*x); k*exp(1i*k*x), -k*exp(-1i*k*x)];
    %matriz inversa
    g=@(k,x) [k*exp(-1i*k*x), exp(-1i*k*x); k*exp(1i*k*x), -exp(1i*k*x)]/(2*k); 

    m=1;
    for w=[0.6957, 1.1216, 2.0200]
        A3=1;
        B3=-A3*exp(2*1i*w*L/v3);
        V=[A3;B3];
        V=g(w/v2,a)*f(w/v3,a)*V;
        A2=V(1); B2=V(2);
        V=g(w/v1,-a)*f(w/v2,-a)*V;
        A1=V(1); B1=V(2);
        suma=integra(A1,B1,w/v1,-L,-a)/v1^2+integra(A2,B2,w/v2,-a,a)/v2^2+
integra(A3,B3,w/v3,a,L)/v3^2;
        subplot(3,1,m)
        m=m+1;
        hold on
        fc=@(x) real(A1*exp(1i*w*x/v1)+B1*exp(-1i*w*x/v1))/sqrt(suma);
        fplot(fc,[-L,-a])
        fc=@(x) real(A2*exp(1i*w*x/v2)+B2*exp(-1i*w*x/v2))/sqrt(suma);
        fplot(fc,[-a,a])
        fc=@(x) real(A3*exp(1i*w*x/v3)+B3*exp(-1i*w*x/v3))/sqrt(suma);
        fplot(fc,[a,L])
        hold off
        grid on
        xlabel('x')
        ylabel('y')
        title(sprintf('w=%1.3f',w))
    end

    function res=integra(A, B, k, x1,x2)
        res=(A*conj(A)+B*conj(B))*(x2-x1)+(A*conj(B)*(exp(2*1i*k*x2)-
exp(2*1i*k*x1))-conj(A)*B*(exp(-2*1i*k*x2)-exp(-2*1i*k*x1)))/(2*1i*k);
    end
end

Cuerda asimétrica

Las densidades o las velocidades de propagación de los segmentos extremos son iguales v₁=v₃, por lo que y(x) es simétrica. Consideremos el caso en el que v₁=1, v₂=2, y v₃=3

Representamos la parte real e imaginaria en el intervalo de frecuencias ω de 0.5 a 2 y marcamos las intersecciones en el eje X

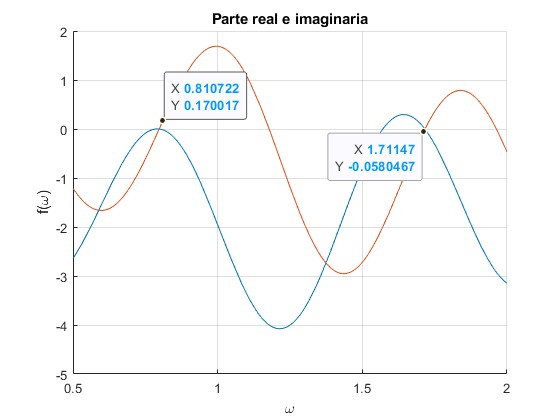
Los ceros de la parte real e imaginaria coinciden para las frecuencias ω=0.81 y 1.71, aproximadamente

Las calculamos

número de intervalos:7
1.5708  1.7163  2.3562  2.5094  3.1416  3.5726  3.9270
número de intervalos:8
0.7978  1.1781  1.7163  1.9635  2.5094  2.7489  3.5343  3.5726

Coinciden las frecuencias, ω=1.7163, 2.5094, 3.5726

Como vemos en la figura anterior, para la frecuencia ω=0.7978, la parte real (color azul) es tangente al eje X, el procedimiento numérico es incapaz de localizar esta raíz

Representamos la amplitud de la onda estacionaria y(x) para las tres primeras frecuencias, ω=0.7978, 1.7163, 2.5094

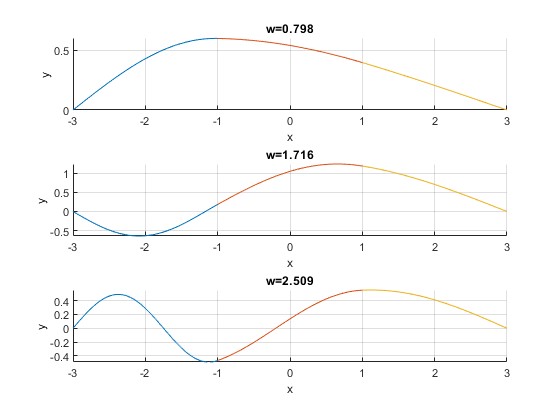
Referencias

Clendenning L. M. A laboratory approach to eigenvalue problem. Am. J. Phys. 36 (10) October 1968, pp. 879-881

Lim Yung-kuo. Problems and Solutions on Mechanics. World Scientific (1994). Problem 1236, pp. 389-393

G. Rodríguez Zurita, Ramón Alvarado Bustos, Rubén Alvarado Bustos, L. E. Zavala Ramírez. Modos de oscilación en cuerdas homogéneas por tercios. Revista Mexicana de Física, 48 (5) Octubre 2002. pp. 463–474.