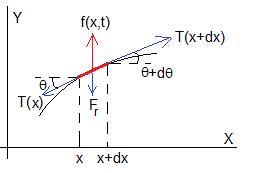
Aplicamos la segunda ley de Newton a un elemento diferencial de cuerda comprendida entre x y x+dx

• T(x), es la fuerza que ejerce la parte izquierda de la cuerda sobre el elemento diferencial

• T(x+dx), es la fuerza que ejerce la parte derecha de la cuerda sobre el elemento diferencial

La componente Y de las fuerzas, dF_y, que actúan sobre dicho elemento diferencial es

${\displaystyle \begin{array}{l}d{F}_y=T(x+dx)·\sin (\theta +d\theta )-T(x)\sin \theta \simeq \hfill \\ \left(T(x)+\frac{dT}{dx}dx\right)·(\sin \theta +\cos \theta ·d\theta )-T(x)\sin \theta =\hfill \\ \frac{d}{dz}\left(\sin \theta ·T(x)\right)·dx\simeq \frac{d}{dz}\left(\tan \theta ·T(x)\right)·dx=\frac{d}{dx}\left(\frac{d\psi }{dx}·T(x)\right)·dx\hfill \end{array}}$

Para ángulos pequeños, hacemos la aproximación sinθ≈tanθ

Otras fuerzas que actúan sobre el elemento diferencial de cuerda son:

• La fuerza de rozamiento proporcional a la velocidad y de sentido contrario a ésta

${\displaystyle -\lambda \frac{\partial \psi (x,t)}{\partial t}dx}$

• La fuerza externa, f(x,t)·dx

Estas tres fuerzas que actúan sobre el elemento diferencial de masa μ(x)dx producen una aceleración a lo largo del eje Y. Teniendo en cuenta, Ψ es una función continua de x y t escribimos, la segunda ley de Newton, fuerza=masa×paceleración

${\displaystyle \frac{\partial }{\partial x}\left(\frac{\partial \psi }{\partial x}T(x)\right)dx+f(x,t)dx-\lambda \frac{\partial \psi }{\partial t}dx=\left(\mu ·dx\right)\frac{{\partial }^2\psi }{\partial t^2}}$

Donde μ(x) es la densidad de una cuerda y T(x) es la tensión en cada punto de la cuerda, supondremos que ambas son constantes

${\displaystyle \frac{{\partial }^2\psi }{\partial t^2}+2\gamma \frac{\partial \psi }{\partial t}-c^2\frac{{\partial }^2\psi }{\partial x^2}=\frac{1}{\mu }f(x,t),c=\sqrt{\frac{T}{\mu }},2\gamma =\frac{\lambda }{\mu }}$

c es la velocidad de propagación de las ondas transversales en la cuerda y γ se denomina constante de amortiguamiento

Condiciones iniciales y de contorno

Para resolver la ecuación diferencial en derivadas parciales que es de segundo orden en x y en t, se precisa especificar dos condiciones inciales: la deformación inicial de la cuerda y la velocidad inicial de cada uno de los puntos de la cuerda

${\displaystyle t=0\{\begin{array}{l}\psi (x\mathrm{,0})={\psi }_0(x)\\ {\frac{\partial \psi (x,t)}{\partial t}|}_{t=0}={\dot{\psi }}_0(x)\end{array}}$

y otras dos condiciones de contorno:

• Un extremo en x=0, es fijo

${\displaystyle \psi (\mathrm{0,}t)=0}$

• El otro extremo en x=l está fijo

${\displaystyle \psi (l,t)=0}$

Modos de oscilación libre

En la página titulada Vibraciones libres de una cuerda sujeta por ambos extremos, estudiamos las soluciones de la ecuación diferencial, sin amortiguamiento γ=0 y sin fuerza externa f(x,t)=0

${\displaystyle \frac{{\partial }^2\psi }{\partial t^2}-c^2\frac{{\partial }^2\psi }{\partial x^2}=0}$

La solución de la ecuación diferencial es

${\displaystyle \psi (x,t)={\displaystyle \sum _{n=1}^{\infty }\sin \left(n\pi \frac{x}{l}\right)\left\{A_n\cos \left(n\pi \frac{c}{l}t\right)+B_n\sin \left(n\pi \frac{c}{l}t\right)\right\}}}$

Esta ecuación describe todos los posibles modos de vibración de la cuerda sujeta por ambos extremos. La vibración particular que experimenta la cuerda está únicamente determinada por las condiciones iniciales, que a su vez determinan los valores de las constantes A_n y B_n.

Modos de oscilación amortiguados

La ecuación diferencial del Movimiento Ondulatorio amortiguado es

${\displaystyle \frac{{\partial }^2\psi }{\partial t^2}+2\gamma \frac{\partial \psi }{\partial t}-c^2\frac{{\partial }^2\psi }{\partial x^2}=0}$

Donde c es la velocidad de propagación de las ondas transversales en una cuerda y γ es la constante de amortiguamiento.

Modos de vibración

Para resolver la ecuación diferencial dividimos la solución en producto de dos funciones una dependiente de x y la otra de t.

${\displaystyle \begin{array}{l}\psi (x,t)=\Phi (x)·T(t)\hfill \\ \begin{array}{l}\Phi (x)\left\{\frac{d^{2}T}{d{t}^2}+2\gamma \frac{dT}{dt}\right\}=c^2\frac{d^2\Phi }{d{x}^2}T(t)\\ T(t)\left\{\frac{d^{2}T}{d{t}^2}+2\gamma \frac{dT}{dt}\right\}=\frac{c^2}{\Phi (x)}\frac{d^2\Phi }{d{x}^2}=-{\omega }_0^2\end{array}\hfill \end{array}}$

Como el miembro izquierdo depende solamente de t y el derecho solamente de x, entonces, igualamos ambos a una constante que denominaremos -ω₀²

${\displaystyle \{\begin{array}{l}\frac{d^2\Phi }{d{x}^2}+\frac{{\omega }_0^2}{c^2}\Phi =0\\ \frac{d^{2}T}{d{t}^2}+2\gamma \frac{dT}{dt}+{\omega }_0^{2}T=0\end{array}}$

Hemos sustituimos una ecuación diferencial en derivadas parciales por dos ecuaciones diferenciales. Ambas ecuaciones tienen soluciones conocidas, ecuación de las oscilaciones libres

${\displaystyle \Phi (x)=C\cos \left(\frac{{\omega }_0}{c}x\right)+D\sin \left(\frac{{\omega }_0}{c}x\right)}$

y ecuación de las oscilaciones amortiguadas

${\displaystyle \{\begin{array}{l}T(t)=\exp \left(-\gamma t\right)\left\{A\sin \left(\omega t\right)+B\cos \left(\omega t\right)\right\}{\omega }_0>\gamma {\omega }^2={\omega }_0^2-{\gamma }^2\\ T(t)=\exp \left(-\gamma t\right)\left\{A\sinh \left(\omega t\right)+B\cosh \left(\omega t\right)\right\}{\omega }_0<\gamma {\omega }^2={\gamma }^2-{\omega }_0^2\end{array}}$

Donde A, B, C y D se determinan a partir de las dos condiciones iniciales y las otras dos de contorno.

Si la cuerda está sujeta por el extremo izquierdo x=0, entonces Φ(0)=0 y C=0. Si está sujeta por el extremo derecho Φ(l)=0, entonces y D no podrá ser nulo en una solución no trivial, sino que

${\displaystyle \sin \left(\frac{{\omega }_0}{c}l\right)=0{\omega }_{0n}=n\pi \frac{c}{l}n=\mathrm{1,2,3...}}$

Las frecuencias ω_0n se denominan naturales o propias de la cuerda, que hemos calculado en el apartado anterior.

${\displaystyle {\Phi }_n(x)=\sin \left(\frac{{\omega }_{0n}}{c}x\right)=\sin \left(n\pi \frac{x}{l}\right)}$

La solución de la ecuación diferencial correspondiente al modo n de vibración de la cuerda es Ψ_n(x,t)=Φ_n(x)·T_n(t)

${\displaystyle \begin{array}{l}\{\begin{array}{l}{\psi }_n(x,t)=\exp \left(-\gamma t\right)\sin \left(n\pi \frac{x}{l}\right)\left\{A_n\sin \left({\omega }_{n}t\right)+B_n\cos \left({\omega }_{n}t\right)\right\}{\omega }_{0n}>\gamma \\ {\psi }_n(x,t)=\exp \left(-\gamma t\right)\sin \left(n\pi \frac{x}{l}\right)\left\{A_n\sinh \left({\omega }_{n}t\right)+B_n\cosh \left({\omega }_{n}t\right)\right\}{\omega }_{0n}<\gamma \end{array}\\ {\omega }_n^2=\left|{\left(n\pi \frac{c}{l}\right)}^2-{\gamma }^2\right|\end{array}}$

donde A_n y B_n son coeficientes que se determinarán más adelante

• Los modos n=1...n₀, tal que n<γl/(πc) corresponden a oscilaciones sobreamortiguadas, que desaparecen al cabo de muy poco tiempo

• Los modos n=n₀+1, n₀+2,...∞, tal que n>γl/(πc) corresponden a oscilaciones amortiguadas

Superposición

La solución general que satisface las condiciones de contorno Φ(0)=0, y Φ(l)=0, es la superposición

${\displaystyle \begin{array}{l}\psi (x,t)={\displaystyle \sum _{n=1}^{\infty }{\psi }_n(x,t)}=\exp \left(-\gamma t\right){\displaystyle \sum _{n=1}^{n_0}\sin \left(n\pi \frac{x}{l}\right)\left\{A_n\sinh \left({\omega }_{n}t\right)+B_n\cosh \left({\omega }_{n}t\right)\right\}}+\\ \exp \left(-\gamma t\right){\displaystyle \sum _{n=n_0+1}^{\infty }\sin \left(n\pi \frac{x}{l}\right)\left\{A_n\sin \left({\omega }_{n}t\right)+B_n\cos \left({\omega }_{n}t\right)\right\}}\end{array}}$

La velocidad de cada punto x de la cuerda en el instante t es

${\displaystyle \begin{array}{l}\frac{\partial \psi (x,t)}{\partial t}=\exp \left(-\gamma t\right){\displaystyle \sum _{n=1}^{n_0}\sin \left(n\pi \frac{x}{l}\right)\left\{-\gamma \left\{A_n\sinh \left({\omega }_{n}t\right)+B_n\cosh \left({\omega }_{n}t\right)\right\}+{\omega }_n\left\{A_n\cosh \left({\omega }_{n}t\right)+B_n\sinh \left({\omega }_{n}t\right)\right\}\right\}}+\\ \exp \left(-\gamma t\right){\displaystyle \sum _{n=n_0+1}^{\infty }\sin \left(n\pi \frac{x}{l}\right)\left\{-\gamma \left\{A_n\sin \left({\omega }_{n}t\right)+B_n\cos \left({\omega }_{n}t\right)\right\}+{\omega }_n\left\{A_n\cos \left({\omega }_{n}t\right)-B_n\sin \left({\omega }_{n}t\right)\right\}\right\}}\end{array}}$

La primera ecuación describe todos los posibles modos de vibración de la cuerda sujeta por ambos extremos. La vibración particular que experimenta la cuerda está únicamente determinada por las condiciones iniciales, que a su vez determinan los valores de las constantes A_n y B_n.

${\displaystyle \begin{array}{l}\psi (x\mathrm{,0})=\psi (0)={\displaystyle \sum _{n=1}^{\infty }{B}_n\sin \left(n\pi \frac{x}{l}\right)}\\ {\frac{\partial \psi (x,t)}{\partial t}|}_{t=0}=\dot{\psi }(0)={\displaystyle \sum _{n=1}^{\infty }\left(-\gamma B_n+{\omega }_n{A}_n\right)\sin \left(n\pi \frac{x}{l}\right)}\end{array}}$

Los valores de las constantes A_n y B_n se determinan de modo análogo a la cuerda sin rozamiento, del primer apartado.

${\displaystyle \begin{array}{l}{B}_n=\frac{2}{l}\underset{0}{\overset{l}{{\displaystyle \int }}}{\psi }_0(x)\sin \left(n\pi \frac{x}{l}\right)dx\hfill \\ -\gamma B_n+{\omega }_n{A}_n=\frac{2}{l}\underset{0}{\overset{l}{{\displaystyle \int }}}{\dot{\psi }}_0(x)\sin \left(n\pi \frac{x}{l}\right)dx\hfill \end{array}}$

Cuerda punzada

En la figura, se muestra la deformación inicial de una cuerda de longitud l

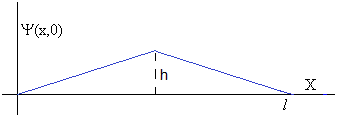
Las condiciones iniciales son

${\displaystyle \begin{array}{l}\psi (x\mathrm{,0})=\{\begin{array}{l}2h\frac{x}{l}0\le x\le \frac{l}{2}\\ 2h\left(1-\frac{x}{l}\right)\frac{l}{2}<x\le l\end{array}\hfill \\ {\frac{\partial \psi (x,t)}{\partial x}|}_{t=0}=0\hfill \end{array}}$

Los coeficientes A_n y B_n (este coeficiente se ha calculado en el apartado titulado 'Cuerda punzada' tomando a=l/2)

${\displaystyle \begin{array}{l}{B}_n=\frac{2}{l}\underset{0}{\overset{l/2}{{\displaystyle \int }}}2h\frac{x}{l}\sin \left(n\pi \frac{x}{l}\right)dx+\frac{2}{l}\underset{l/2}{\overset{l}{{\displaystyle \int }}}2h\left(1-\frac{x}{l}\right)\sin \left(n\pi \frac{x}{l}\right)dx=\frac{8h}{n^2{\pi }^2}\sin \left(n\frac{\pi }{2}\right)\\ B_n=\{\begin{array}{l}0n\text{ par}\\ \frac{8h}{n^2{\pi }^2}{\left(-1\right)}^{\frac{n-1}{2}}n\text{ impar}\end{array}\\ A_n=\frac{\gamma }{{\omega }_n}{B}_n\end{array}}$

>>syms x h L n;
>> assume(n,'integer')
>> an=2*(int(x*sin(n*pi*x/L),x,0,L/2)*2*h/L+int((1-x/L)*sin(n*pi*x/L),
x,L/2,L)*2*h)/L;
>> simplify(an)
ans =
-(4*(-1)^(n/2 - 1/2)*h*((-1)^n - 1))/(n^2*pi^2)

Cuando el amortiguamiento γ es pequeño, n₀<1, solamente hay términos correspondientes a oscilaciones amortiguadas, ω_0n>γ

${\displaystyle \begin{array}{l}\psi (x,t)=\exp \left(-\gamma t\right){\displaystyle \sum _{n=1}^{\infty }\sin \left(n\pi \frac{x}{l}\right)\left\{A_n\sin \left({\omega }_{n}t\right)+B_n\cos \left({\omega }_{n}t\right)\right\}}=\\ \frac{8h}{{\pi }^2}\exp \left(-\gamma t\right){\displaystyle \sum _{n=\mathrm{1,3,5...}}^{\infty }\frac{{\left(-1\right)}^{\frac{n-1}{2}}}{n^2}\sin \left(n\pi \frac{x}{l}\right)\left\{\frac{\gamma }{{\omega }_n}\sin \left({\omega }_{n}t\right)+\cos \left({\omega }_{n}t\right)\right\}}\end{array}}$

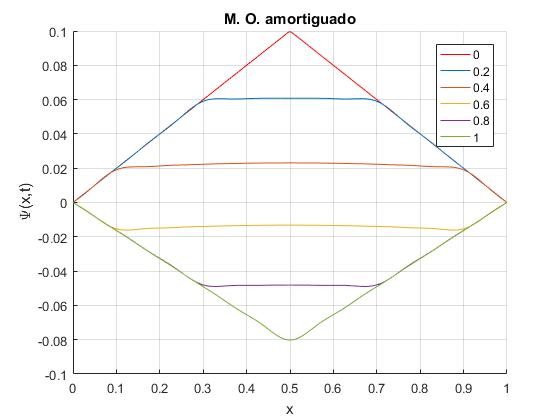
En el siguiente script reperesentamos el estado de una cuerda de longitud l=1, en varios instantes t=0, 0.2, 0.4, 0.6, 0.8 y 1.

• La velocidad de propagación de las ondas en la cuerda es c=1.

• Se desplaza el punto medio de la cuerda una distancia h=0.1 en el instante t=0 y a continuación, se suelta.

• La constante de amortiguamiento γ=0.2, de modo que γl/(πc)=0.06<1. Todos los modos de vibración corresponden a oscilaciones amortiguadas (n·πc/l)>γ, n=1,2,3...

• Se toman 10 términos del desarrollo en serie n=1,3,5...17,19

Primero, dibujamos el estado inicial de la cuerda en el instante t=0, en color rojo.

g=0.2; %constante de amortiguamiento
c=1; %velocidad de propagación
L=1; %longitud de la cuerda
h=0.1; %deformación cuerda

hold on
x=linspace(0,L,200);
y=(2*h*x/L).*(heaviside(x)-heaviside(x-L/2))+(2*h*(1-x/L)).
*(heaviside(x-L/2)-heaviside(x-L));
plot(x,y, 'r','displayName',num2str(0))

for t=0.2:0.2:1
    yy=zeros(1,length(x));
    for n=1:2:19
        wn=sqrt((n*pi*c/L)^2-g^2);
        yy=yy+(-1)^((n-1)/2)*sin(n*pi*x/L)*(g*sin(wn*t)/wn+cos(wn*t))/n^2;
    end
    yy=yy*8*h*exp(-g*t)/pi^2;
    plot(x,yy, 'displayName',num2str(t))
end
hold off
grid on
legend('-DynamicLegend','location','northeast')
xlabel('x')
ylabel('\Psi(x,t)')
title('M. O. amortiguado')

Transformada de Laplace

Alternativamente, utilizamos la transfromada de Laplace para deducir la solución de la ecuación diferencial de los modos de oscilación amortiguado, siguiendo los mismos pasos que en las oscilaciones amortiguadas

Para una cuerda cuyos extremos están fijos buscamos una solución de la forma

${\displaystyle \psi (x,t)={\displaystyle \sum _{n=1}^{\infty }{u}_n(t)\sin \left(n\pi \frac{x}{l}\right)}}$

Sustituimos en la ecuación diferencial

${\displaystyle {\displaystyle \sum _{n=1}^{\infty }\left\{\frac{d^2{u}_n}{d{t}^2}+2\gamma \frac{d{u}_n}{dt}+c^2{\left(\frac{n\pi }{l}\right)}^2{u}_n\right\}\sin \left(\frac{n\pi }{l}x\right)}=0}$

Multiplicamos por sin(mπx/l) e integramos entre 0 y l. Teniendo en cuenta el resultado de las integrales

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{l}{\int }}{\sin }^2\left(n\pi \frac{x}{l}\right)dx}=\frac{l}{2}\hfill \\ {\displaystyle \underset{0}{\overset{l}{\int }}\sin \left(n\pi \frac{x}{l}\right)\sin \left(m\pi \frac{x}{l}\right)dx}=0m\ne n\hfill \end{array}}$

Se obtiene, un sistema de infinitas ecuaciones diferenciales de segundo orden, n=1,2,3...

${\displaystyle \begin{array}{l}{\displaystyle \sum _{n=1}^{\infty }\left\{\frac{d^2{u}_n}{d{t}^2}+2\gamma \frac{d{u}_n}{dt}+c^2{\left(\frac{n\pi }{l}\right)}^2{u}_n\right\}\sin \left(\frac{n\pi }{l}x\right)}=0\\ \frac{d^2{u}_n}{d{t}^2}+2\gamma \frac{d{u}_n}{dt}+{\omega }_{0n}^2{u}_n=0\end{array}}$

Aplicando la transformada de Laplace a la ecuación diferencial, con las condiciones iniciales

${\displaystyle \{\begin{array}{l}{u}_n(0)=u_{0n}\\ {\frac{d{u}_n}{dt}|}_{t=0}=v_{0n}\end{array}}$

So obtiene

${\displaystyle \begin{array}{l}\left(s^{2}F(s)-s·u_n(0)-{\frac{d{u}_n}{dt}|}_{t=0}\right)+2\gamma \left(sF(s)-u_n(0)\right)+{\omega }_{0n}^{2}F(s)=0\\ \left(s^{2}F(s)-s·u_{0n}-v_{0n}\right)+2\gamma \left(sF(s)-u_{0n}\right)+{\omega }_{0n}^{2}F(s)=0\\ F(s)=\frac{s{u}_{0n}+2\gamma u_{0n}+v_{0n}}{s^2+2\gamma s+{\omega }_{0n}^2}\end{array}}$

Escribimos F(s) de modo que se pueda aplicar transformada inversa de Laplace mirando directamente a la tabla de transformadas.

${\displaystyle \begin{array}{l}F(s)=\frac{u_{0n}(s+\gamma )}{{\left(s+\gamma \right)}^2+\left({\omega }_{0n}^2-{\gamma }^2\right)}+\frac{(\gamma u_{0n}+v_{0n})}{\sqrt{{\omega }_{0n}^2-{\gamma }^2}}\frac{\sqrt{{\omega }_{0n}^2-{\gamma }^2}}{{\left(s+\gamma \right)}^2+\left({\omega }_{0n}^2-{\gamma }^2\right)}\\ u_n(t)=u_{0n}\exp \left(-\gamma t\right)\cos ({\omega }_{n}t)+\frac{\gamma u_{0n}+v_{0n}}{{\omega }_n}\exp \left(-\gamma t\right)\sin ({\omega }_{n}t)\end{array}}$

con ${\omega }_n^2={\omega }_{0n}^2-{\gamma }^2$, frecuencia de la oscilación amortiguada

Condiciones iniciales

La forma inicial de la cuerda es punzada, como en el apartado anterior

${\displaystyle \begin{array}{l}\psi (x\mathrm{,0})={\displaystyle \sum _{n=1}^{\infty }{u}_n(0)\sin \left(n\pi \frac{x}{l}\right)}=\{\begin{array}{l}2h\frac{x}{l}0\le x\le \frac{l}{2}\\ 2h\left(1-\frac{x}{l}\right)\frac{l}{2}<x\le l\end{array}\\ {\frac{\partial \psi (x,t)}{\partial x}|}_{t=0}={\displaystyle \sum _{n=1}^{\infty }{\frac{d{u}_n}{dt}|}_{t=0}\sin \left(n\pi \frac{x}{l}\right)=}0\end{array}}$

Despejamos u_0n=u_n(0) en la primera ecuación

${\displaystyle \begin{array}{l}{u}_n(0){\displaystyle \underset{0}{\overset{l}{\int }}{\sin }^2\left(n\pi \frac{x}{l}\right)}dx=\underset{0}{\overset{l/2}{{{\displaystyle \int }}^{\text{}}}}\left(2h\frac{x}{l}\right)\sin \left(n\pi \frac{x}{l}\right)dx+\underset{l}{\overset{l/2}{{{\displaystyle \int }}^{\text{}}}}2h\left(1-\frac{x}{l}\right)\sin \left(n\pi \frac{x}{l}\right)dx\\ u_{0n}=u_n(0)=\frac{8h}{n^2{\pi }^2}\sin \left(n\frac{\pi }{2}\right)\end{array}}$

Despejamos v_0n en la segunda

${\displaystyle {v_{0n}=\frac{d{u}_n}{dt}|}_{t=0}=0}$

Obtenemos el mismo resultado final

${\displaystyle \begin{array}{l}{u}_n(t)=\frac{8h}{n^2{\pi }^2}\sin \left(n\frac{\pi }{2}\right)\exp \left(-\gamma t\right)\left\{\cos ({\omega }_{n}t)+\frac{\gamma }{{\omega }_n}\sin ({\omega }_{n}t)\right\}\\ \psi (x,t)=\frac{8h}{{\pi }^2}\exp \left(-\gamma t\right){\displaystyle \sum _{n=\mathrm{1,3,...}}^{\infty }\frac{{\left(-1\right)}^{\frac{n-1}{2}}}{n^2}\left\{\cos ({\omega }_{n}t)+\frac{\gamma }{{\omega }_n}\sin ({\omega }_{n}t)\right\}\sin \left(n\pi \frac{x}{l}\right)}\end{array}}$

Oscilaciones amortiguadas de una cuerda que cae

En este apartado, examinamos el efecto del peso en el movimiento amortiguado de la cuerda. Supongamos una cuerda sujeta por ambos extremos, que se deforma inicialmente desplazándola verticalmente y se suelta. La ecuación del movimiento es

${\displaystyle \frac{{\partial }^{2}y}{\partial t^2}+2\gamma \frac{\partial y}{\partial t}-c^2\frac{{\partial }^{2}y}{\partial x^2}=-g,c=\sqrt{\frac{T}{\mu }}}$

En el estado estacionario, después de un tiempo grande, t→∞

${\displaystyle \begin{array}{l}\frac{d^{2}y}{d{x}^2}=\frac{g}{c^2}\\ \frac{dy}{dx}=\frac{g}{c^2}x+C_1\\ y=\frac{1}{2}\frac{g}{c^2}x+C_{1}x+C_2\end{array}}$

Se trata de las ecuaciones de un movimiento uniformemente acelerado. Se calcula las constantes C₁ y C₂, sabiendo que la cuerda está fija en sus extremos y(0)=0, y(l)=0

${\displaystyle y(x,\infty )=-\frac{1}{2}\frac{g}{c^2}(l-x)x}$

El estado final de la cuerda es una parábola, independiente de la deformación inicial

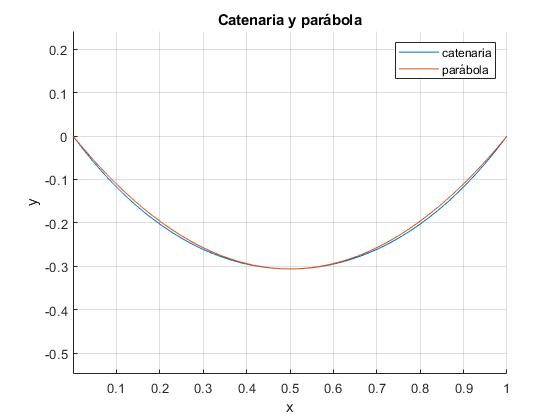
La catenaria y la parábola

La forma de una cuerda sujeta por sus dos extremos es una catenaria. Cuando la flecha

${\displaystyle h=\frac{1}{2}\frac{g}{c^2}\left(l-\frac{l}{2}\right)\frac{l}{2}=\frac{1}{8}\frac{g{l}^2}{c^2}}$

es pequeña, la parábola describe aproximadamente la forma de la cuerda

Representamos una catenaria cuyos extremos disten 2a=l y cuya flecha sea h

• Distancia entre los extremos, aproximadamente igual a la longitud de la cuerda, l=1
• Velocidad de propagación del movimiento ondulatorio, c=2

L=1; %distancia entre los extremos de la cuerda
a=L/2; %distancia 2a
c=2; %velocidad de propagación
h=9.8*L^2/(8*c^2); %flecha
hold on
f=@(x) cosh(x*a)-1-x*h; %dada la flecha se calcula gamma
gamma=fzero(f,[0.1 100]);
f=@(x) (cosh(gamma*(x-a))-cosh(gamma*a))/gamma; %catenaria
fplot(f,[0,2*a]);
fplot(@(x) -9.8*(L-x).*x/(2*c^2), [0,L]) %parábola
hold off
axis equal
grid on
legend('catenaria','parábola')
xlabel('x');
ylabel('y');
title('Catenaria y parábola')

Solución de la ecuación diferencial en derivadas parciales

Para una cuerda cuyos extremos están fijos buscamos una solución de la forma

${\displaystyle y(x,t)={\displaystyle \sum _{n=1}^{\infty }{u}_n(t)\sin \left(n\pi \frac{x}{l}\right)}}$

Sustituimos en la ecuación diferencial en derivadas parciales

${\displaystyle {\displaystyle \sum _{n=1}^{\infty }\left\{\frac{d^2{u}_n}{d{t}^2}+2\gamma \frac{d{u}_n}{dt}+c^2{\left(\frac{n\pi }{l}\right)}^2{u}_n\right\}\sin \left(\frac{n\pi }{l}x\right)}=-g}$

Multiplicamos por sin(mπx/l) e integramos entre 0 y l.

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{l}{\int }}\left({\displaystyle \sum _{n=1}^{\infty }\left(\frac{d^2{u}_n}{d{t}^2}+2\gamma \frac{d{u}_n}{dt}+c^2{\left(\frac{n\pi }{l}\right)}^2{u}_n\right)\sin \left(\frac{n\pi }{l}x\right)}\right)}\sin \left(\frac{m\pi }{l}x\right)dx=-{\displaystyle \underset{0}{\overset{l}{\int }}g\sin \left(\frac{m\pi }{l}x\right)dx}\\ {\displaystyle \sum _{n=1}^{\infty }\left\{\left(\frac{d^2{u}_n}{d{t}^2}+2\gamma \frac{d{u}_n}{dt}+c^2{\left(\frac{n\pi }{l}\right)}^2{u}_n\right){\displaystyle \underset{0}{\overset{l}{\int }}\sin \left(\frac{n\pi }{l}x\right)\sin \left(\frac{m\pi }{l}x\right)dx}\right\}}=-{\displaystyle \underset{0}{\overset{l}{\int }}g\sin \left(\frac{m\pi }{l}x\right)dx}\\ \frac{l}{2}\left(\frac{d^2{u}_n}{d{t}^2}+2\gamma \frac{d{u}_n}{dt}+c^2{\left(\frac{n\pi }{l}\right)}^2{u}_n\right)=\{\begin{array}{l}\mathrm{0,}n\text{ par}\\ -\frac{2gl}{n\pi },n\text{ impar}\end{array}\end{array}}$

La solución de esta ecuación diferencial,

${\displaystyle \begin{array}{l}\{\begin{array}{l}{u}_n(x,t)=\exp (-\gamma t)\{A_n\sin ({\omega }_{n}t)+B_n\cos ({\omega }_{n}t)\}+C_n{\omega }_{0n}>\gamma \\ u_n(x,t)=\exp (-\gamma t)\{A_n\sinh ({\omega }_{n}t)+B_n\cosh ({\omega }_{n}t)\}+C_n{\omega }_{0n}<\gamma \end{array}\hfill \\ \begin{array}{l}{\omega }_n^2=\left|{\left(n\pi \frac{c}{l}\right)}^2-{\gamma }^2\right|\\ C_n=\{\begin{array}{l}\mathrm{0,}n\text{ par}\\ -\frac{4g{l}^2}{c^2{n}^3{\pi }^3},n\text{ impar}\end{array}\end{array}\hfill \end{array}}$

C_n es la solución particular de la ecuación diferencial. Supondremos que el amortiguamiento γ es pequeño y se cumple que ω_0n>γ para todos los modos de vibración

${\displaystyle y(x,t)={\displaystyle \sum _{n=1}^{\infty }{u}_n(x,t)\sin \left(n\pi \frac{x}{l}\right)}={\displaystyle \sum _{n=1}^{\infty }\left\{\exp (-\gamma t)\left(A_n\sin ({\omega }_{n}t)+B_n\cos ({\omega }_{n}t)\right)+C_n\right\}\sin \left(n\pi \frac{x}{l}\right)}}$

La velocidad de cada punto x de la cuerda en el instante t es

${\displaystyle \frac{\partial \psi (x,t)}{\partial t}={\displaystyle \sum _{n=1}^{\infty }\left\{-\gamma \exp (-\gamma t)\left(A_n\sin ({\omega }_{n}t)+B_n\cos ({\omega }_{n}t)\right)+\exp (-\gamma t){\omega }_n\left(A_n\cos ({\omega }_{n}t)-B_n\sin ({\omega }_{n}t)\right)\right\}\sin \left(n\pi \frac{x}{l}\right)}}$

La vibración particular que experimenta la cuerda está únicamente determinada por las condiciones iniciales, que a su vez determinan los valores de las constantes A_n y B_n.

${\displaystyle \begin{array}{l}\psi (x\mathrm{,0})=\psi (0)={\displaystyle \sum _{n=1}^{\infty }\left(B_n+C_n\right)\sin \left(n\pi \frac{x}{l}\right)}\hfill \\ {\frac{\partial \psi (x,t)}{\partial t}|}_{t=0}=\dot{\psi }(0)={\displaystyle \sum _{n=1}^{\infty }\left(-\gamma B_n+{\omega }_n{A}_n\right)\sin \left(n\pi \frac{x}{l}\right)}\hfill \end{array}}$

En la figura, se muestra la deformación inicial de una cuerda de longitud l

Las condiciones iniciales son

${\displaystyle \begin{array}{l}\psi (x\mathrm{,0})=\{\begin{array}{l}2h\frac{x}{l}0\le x\le \frac{l}{2}\\ 2h\left(1-\frac{x}{l}\right)\frac{l}{2}<x\le l\end{array}\hfill \\ {\frac{\partial \psi (x,t)}{\partial x}|}_{t=0}=0\hfill \end{array}}$

Los coeficientes A_n y B_n se calculan de forma similar al primer apartado

${\displaystyle \begin{array}{l}{B}_n+C_n=\frac{2}{l}{\displaystyle \underset{l/2}{\overset{0}{\int }}2h\frac{x}{l}\sin \left(n\pi \frac{x}{l}\right)dx}+\frac{2}{l}{\displaystyle \underset{l/2}{\overset{l}{\int }}2h\left(1-\frac{x}{l}\right)\sin \left(n\pi \frac{x}{l}\right)dx}=\frac{8h}{n^2{\pi }^2}\sin \left(n\frac{\pi }{2}\right)\hfill \\ B_n=\{\begin{array}{l}0n \text{par}\hfill \\ \frac{8h}{n^2{\pi }^2}{(-1)}^{\frac{n-1}{2}}+\frac{4g{l}^2}{c^2{n}^3{\pi }^3}n \text{impar}\hfill \end{array}\hfill \\ A_n=\frac{\gamma }{{\omega }_n}{B}_n\hfill \end{array}}$

El resultado final es

${\displaystyle \begin{array}{l}y(x,t)={\displaystyle \sum _{n=\mathrm{1,3,5...}}^{\infty }\left\{\exp (-\gamma t)\left(\frac{8h}{n^2{\pi }^2}{(-1)}^{\frac{n-1}{2}}+\frac{4g{l}^2}{c^2{n}^3{\pi }^3}\right)\left(\frac{\gamma }{{\omega }_n}\sin ({\omega }_{n}t)+\cos ({\omega }_{n}t)\right)-\frac{4g{l}^2}{c^2{n}^3{\pi }^3}\right\}\sin \left(n\pi \frac{x}{l}\right)}\\ {\omega }_n^2={\left(n\pi \frac{c}{l}\right)}^2-{\gamma }^2\end{array}}$

Después de un tiempo muy grande, t→∞

${\displaystyle y(x,\infty )={\displaystyle \sum _{n=\mathrm{1,3,5...}}^{\infty }\left\{-\frac{4g{l}^2}{c^2{n}^3{\pi }^3}\right\}\sin \left(n\pi \frac{x}{l}\right)=-\frac{1}{2}\frac{g}{c^2}(l-x)x}}$

Consideremos el siguiente caso:

• Longitud de la cuerda, L=1 m
• Deformación vertical, h=0.1
• Velocidad de propagacion, c=4
• Constante de amortiguamiento, γ=0.2

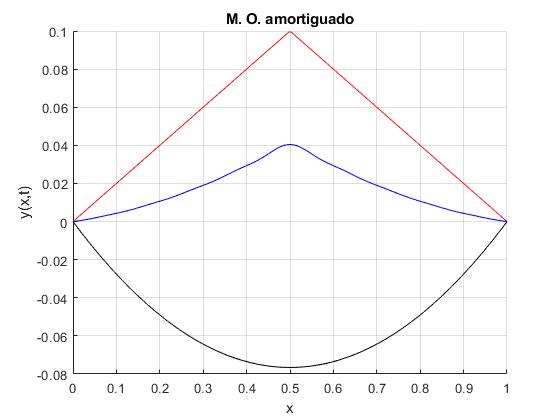
Representamos la deformación inicial (en color azul), la final (negro) y en el instante t=2, (rojo). Para mostrar las deformaciones de la cuerda, la escala vertical es mayor que la horizontal

g=0.2; %constante de amortiguamiento
c=4; %velocidad de propagación
L=1; %longitud de la cuerda
h=0.1; %deformación cuerda

hold on
x=linspace(0,L,200);
%estado inicial
y=(2*h*x/L).*(heaviside(x)-heaviside(x-L/2))+(2*h*(1-x/L)).*
(heaviside(x-L/2)-heaviside(x-L));
plot(x,y, 'r','displayName',num2str(0))
t=2; %instante
yy=zeros(1,length(x));
for n=1:2:19
    wn=sqrt((n*pi*c/L)^2-g^2);
    yy=yy+(exp(-g*t)*((-1)^((n-1)/2)*8*h/(n^2*pi^2)+4*9.8*L^2/(c^2*n^3*pi^3))
*(g*sin(wn*t)/wn+cos(wn*t))-4*9.8*L^2/(c^2*n^3*pi^3))*sin(n*pi*x/L);
end
plot(x,yy, 'b')
plot(x,9.8*(x.^2-L*x)/(2*c^2),'k') %estado final
hold off
grid on
xlabel('x')
ylabel('y(x,t)')
title('M. O. amortiguado')

Actividades

La cuerda se desplaza h desde la posición l/2 y se suelta. Se estudia las oscilaciones amortiguadas, solamente o con el efecto del peso de la cuerda, activando el botón de radio titulado gravedad Si o gravedad No

Se introduce

• La constante γ de amortiguamiento, en el control titulado Amortiguamiento
• Se ha fijado el máximo desplazamiento h=0.1, la longitud de la cuerda l=1 y la velocidad de propagación de las ondas en la cuerda c=4

Se pulsa el botón titulado Nuevo

Se suelta la cuerda y se observa su movimiento, en la parte superior se proporciona el dato del tiempo t

En color azul, el estado inicial, en color rojo la deformación de la cuerda en el instante t y en color negro, cuando t→∞

Referencias

N Gauthier. Exact expressions for the amplitudes and damped normal frequencies of taut vibrating linear string of coupled masses. Eur. J. Phys. 29 (2008) N21-N29