Supongamos una cuerda de densidad lineal μ, que está libre en un extremo y en el otro está atado a un eje vertical que gira con velocidad angular constante ω. Despreciando la gravedad vamos a determinar la ecuación de la propagación de las ondas transversales en la cuerda.

Ecuación diferencial del movimiento ondulatorio

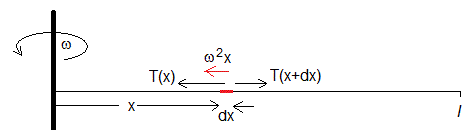
Consideremos un elemento diferencial de cuerda situado entre x y x+dx, de masa μ·dx.

La parte izquierda de la cuerda, ejerce una fuerza T(x) sobre dicho elemento, la parte derecha de la cuerda ejerce una fuerza T(x+dx). Su aceleración es ω²x dirigida radialmente hacia el centro de la circunferenca que describe. La segunda ley de Newton se escribe

T(x)-T(x+dx)=(μ·dx)ω²x

-dT=μω²x·dx

Sabiendo que T(l)=0, integramos

${\displaystyle \begin{array}{l}{\displaystyle \underset{x}{\overset{l}{\int }}dT}=-\mu {\omega }^2{\displaystyle \underset{x}{\overset{l}{\int }}x·dx}\\ T(x)=\frac{1}{2}\mu {\omega }^2\left(l^2-x^2\right)\end{array}}$

Consideremos una cuerda cuya tensión es T(x). En el equilibrio, la cuerda está en línea recta. Vamos a ver lo que ocurre cuando se desplaza verticamente, un elemento de longitud dx, situado en la posición x de la cuerda, una cantidad Ψ respecto de la posición de equilibrio.

Dibujamos las fuerzas que actúan sobre el elemento diferencial y calculamos la aceleración del mismo, aplicando la segunda ley de Newton.

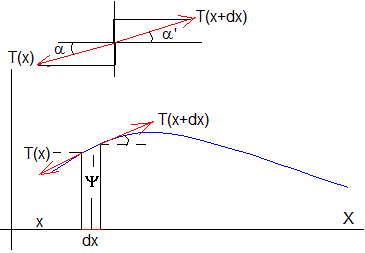
• La componente vertical de la fuerza que ejerce la parte izquierda de la cuerda sobre el elemento diferencial dx es

${\displaystyle T(x)\sin \alpha \approx T(x)\tan \alpha ={T\frac{\partial \psi }{\partial x}|}_x}$

• La componente vertical de la fuerza que ejerce la parte derecha de la cuerda sobre el elemento diferencial dx es

${\displaystyle T(x+dx)\sin \alpha \text{'}\approx T(x+dx)\tan \alpha \text{'}={T\frac{\partial \psi }{\partial x}|}_{x+dx}}$

Siempre que la amplitud del movimiento ondulatorio transversal sea pequeña, se puede hacer la aproximación sinα≈tanα

La fuerza vertical neta es el producto de la masa porla aceleración vertical

${\displaystyle \begin{array}{l}{T\frac{\partial \psi }{\partial x}|}_{x+dx}-{T\frac{\partial \psi }{\partial x}|}_x=\left(\mu dx\right)\frac{{\partial }^2\psi }{\partial t^2}\\ \frac{\partial }{\partial x}\left(T\frac{\partial \psi }{\partial x}\right)dx=\mu \frac{{\partial }^2\psi }{\partial t^2}dx\\ \frac{1}{2}{\omega }^2\frac{\partial }{\partial x}\left(\left(l^2-x^2\right)\frac{\partial \psi }{\partial x}\right)=\frac{{\partial }^2\psi }{\partial t^2}\end{array}}$

Modos de vibración

Resolveremos esta ecuación diferencial en derivadas parciales con la siguiente condición de contorno: Ψ(0,t)=0. Un extremo de la cuerda está atado al eje vertical de rotación

Las condiciones iniciales

${\displaystyle \begin{array}{l}\psi (x\mathrm{,0})={\psi }_0(x)\\ {\frac{\partial \psi (x,t)}{\partial t}|}_{t=0}={\dot{\psi }}_0(x)\end{array}}$

Para resolver la ecuación diferencial dividimos la solución en producto de dos funciones una dependiente de x y la otra de t.

${\displaystyle \begin{array}{l}\psi (x,t)=\Phi (x)·T(t)\\ \frac{2}{{\omega }^2}\frac{1}{T(t)}\frac{d^{2}T}{d{t}^2}=\frac{1}{\Phi (x)}\frac{d}{dx}\left((l^2-x^2)\frac{d\Phi }{dx}\right)=-\lambda \\ \{\begin{array}{l}\frac{d^{2}T}{d{t}^2}+\frac{1}{2}{\omega }^2\lambda T(t)=0\\ \frac{d}{dx}\left((l^2-x^2)\frac{d\Phi }{dx}\right)+\lambda \Phi (x)=0\end{array}\end{array}}$

Hemos sustituimos una ecuación diferencial en derivadas parciales por dos ecuaciones diferenciales. La primera tiene una solución sencilla

${\displaystyle T(t)=A\cos \left(\omega \sqrt{\frac{\lambda }{2}}t\right)+B\sin \left(\omega \sqrt{\frac{\lambda }{2}}t\right)}$

Para la segunda, sustituimos x=lξ

${\displaystyle \begin{array}{l}\frac{d}{d\xi }\left((1-{\xi }^2)\frac{d\Phi }{d\xi }\right)+\lambda \Phi =0\\ (1-{\xi }^2)\frac{d^2\Phi }{d{\xi }^2}-2\xi \frac{d\Phi }{d\xi }+\lambda \Phi =0\end{array}}$

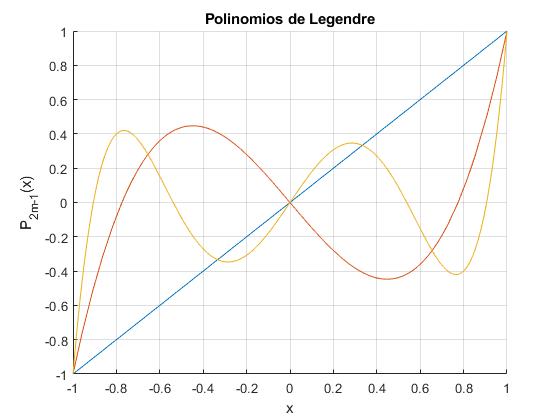
Esta es la ecuación diferencial de Legendre, con λ=n(n+1), donde n es un entero positivo. La solución de la ecuación diferencial son los polinomios de Legendre P_n(ξ) definidos en el intervalo [-1,1].

Los polinomios que cumplen P_n(0)=0, son aquellos en los que n es un número impar 1,3,5,..2m-1, donde m es un entero positivo. Estos polinomos son antisimétricos, P_n(ξ)=-P_n(-ξ), con n=2m-1

hold on
for m=1:3
    fplot(@(x) legendreP(2*m-1,x),[-1,1])
end
hold off
grid on
xlabel('x')
ylabel('P_{2m-1}(x)')
title('Polinomios de Legendre')

La solución de las ecuaciones diferenciales para el modo m es

${\displaystyle \begin{array}{l}{\Phi }_m(x)=P_{2m-1}\left(\frac{x}{l}\right)\\ T_m(t)=A_m\cos \left(\omega \sqrt{m(2m-1)}t\right)+B_m\sin \left(\omega \sqrt{m(2m-1)}t\right),m=\mathrm{1,2,3...}\end{array}}$

Las frecuencias de los modos normales de vibración de la cuerda son

${\displaystyle {\omega }_n=\omega \sqrt{m(2m-1)}}$

Superposición

La solución general que satisface la condición de contorno Ψ(0,t)=0, es la superposición

${\displaystyle \begin{array}{l}\psi (x,t)={\displaystyle \sum _{m=1}^{\infty }{\Phi }_m(x)T_m(t)}=\\ {\displaystyle \sum _{m=1}^{\infty }{P}_{2m-1}\left(\frac{x}{l}\right)\left(A_m\cos \left(\omega \sqrt{m(2m-1)}t\right)+B_m\sin \left(\omega \sqrt{m(2m-1)}t\right)\right)}\end{array}}$

Donde los coeficientes A_m y B_m se determinan a partir de las condiciones iniciales.

${\displaystyle \begin{array}{l}\psi (x\mathrm{,0})={\psi }_0(x)={\displaystyle \sum _{m=1}^{\infty }{A}_m{P}_{2m-1}\left(\frac{x}{l}\right)}\\ {\frac{\partial \psi (x,t)}{\partial t}|}_{t=0}={\dot{\psi }}_0(x)={\displaystyle \sum _{m=1}^{\infty }\omega \sqrt{m(2m-1)}{B}_m{P}_{2m-1}\left(\frac{x}{l}\right)}\end{array}}$

Teniendo en cuenta la propiedad de los polinomios de Legendre

${\displaystyle {\displaystyle \underset{-1}{\overset{1}{\int }}{P}_m(x)P_n(x)dx}=\{\begin{array}{l}\frac{2}{2n+1},m=n\\ \mathrm{0,}m\ne n\end{array}}$

Calculamos los coeficientes A_m

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{l}{\int }}{\psi }_0(x)P_{2k-1}\left(\frac{x}{l}\right)dx}={\displaystyle \underset{0}{\overset{l}{\int }}\left({\displaystyle \sum _{m=1}^{\infty }{A}_m{P}_{2m-1}\left(\frac{x}{l}\right)}\right)P_{2k-1}\left(\frac{x}{l}\right)}\\ {\displaystyle \underset{0}{\overset{l}{\int }}{\psi }_0(x)P_{2k-1}\left(\frac{x}{l}\right)dx}={\displaystyle \sum _{m=1}^{\infty }{A}_m{\displaystyle \underset{0}{\overset{l}{\int }}{P}_{2m-1}\left(\frac{x}{l}\right)P_{2k-1}\left(\frac{x}{l}\right)dx}}\\ {\displaystyle \underset{0}{\overset{l}{\int }}{\psi }_0(x)P_{2k-1}\left(\frac{x}{l}\right)dx}=\frac{l}{2}{\displaystyle \sum _{m=1}^{\infty }{A}_m{\displaystyle \underset{-1}{\overset{1}{\int }}{P}_{2m-1}\left(\xi \right)P_{2k-1}\left(\xi \right)d\xi }}\\ {\displaystyle \underset{0}{\overset{l}{\int }}{\psi }_0(x)P_{2m-1}\left(\frac{x}{l}\right)dx}=\frac{l}{2}{A}_m\frac{2}{2(2m-1)+1}\\ A_m=\frac{4m-1}{l}{\displaystyle \underset{0}{\overset{l}{\int }}{\psi }_0(x)P_{2m-1}\left(\frac{x}{l}\right)dx}\end{array}}$

Calculamos los coeficientes B_m

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{l}{\int }}{\dot{\psi }}_0(x)P_{2k-1}\left(\frac{x}{l}\right)dx}={\displaystyle \underset{0}{\overset{l}{\int }}\left({\displaystyle \sum _{m=1}^{\infty }\omega \sqrt{m(2m-1)}{B}_m{P}_{2m-1}\left(\frac{x}{l}\right)}\right)P_{2k-1}\left(\frac{x}{l}\right)}\\ {\displaystyle \underset{0}{\overset{l}{\int }}{\dot{\psi }}_0(x)P_{2k-1}\left(\frac{x}{l}\right)dx}={\displaystyle \sum _{m=1}^{\infty }\omega \sqrt{m(2m-1)}{B}_m{\displaystyle \underset{0}{\overset{l}{\int }}{P}_{2m-1}\left(\frac{x}{l}\right)P_{2k-1}\left(\frac{x}{l}\right)dx}}\\ {\displaystyle \underset{0}{\overset{l}{\int }}{\dot{\psi }}_0(x)P_{2k-1}\left(\frac{x}{l}\right)dx}=\frac{l}{2}{\displaystyle \sum _{m=1}^{\infty }\omega \sqrt{m(2m-1)}{B}_m{\displaystyle \underset{-1}{\overset{1}{\int }}{P}_{2m-1}\left(\xi \right)P_{2k-1}\left(\xi \right)d\xi }}\\ {\displaystyle \underset{0}{\overset{l}{\int }}{\dot{\psi }}_0(x)P_{2m-1}\left(\frac{x}{l}\right)dx}=\frac{l}{2}\omega \sqrt{m(2m-1)}{B}_m\frac{2}{2(2m-1)+1}\\ B_m=\frac{4m-1}{l\omega \sqrt{m(2m-1)}}{\displaystyle \underset{0}{\overset{l}{\int }}{\dot{\psi }}_0(x)P_{2m-1}\left(\frac{x}{l}\right)dx}\end{array}}$

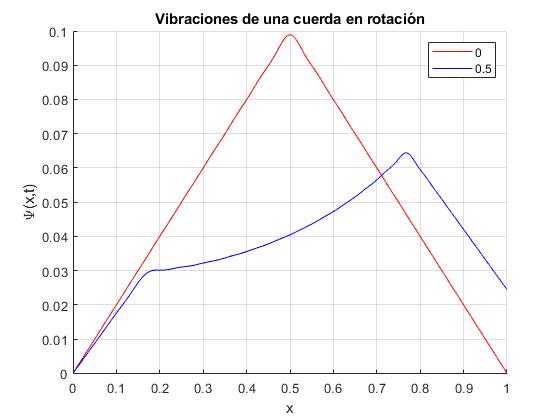
Ejemplo

Se deforma inicialmente la cuerda tal como se muestra en la figura. Las condiciones iniciales son

${\displaystyle \begin{array}{l}\psi (x\mathrm{,0})=\{\begin{array}{l}2h\frac{x}{l}0\le x<\frac{l}{2}\\ 2h\left(1-\frac{x}{l}\right)\frac{l}{2}\le x<l\end{array}\hfill \\ {\frac{\partial \psi (x,t)}{\partial x}|}_{t=0}=0\hfill \end{array}}$

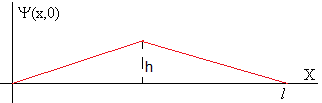
Los coeficientes B_m=0

Calculamos los coeficientes A_m, respresentando el estado inicial de la cuerda t=0, y en el instante t=0.5. Los datos son:

• Longitud de la cuerda, l=1
• Velocidad angular de rotación, ω=1
• Deformación en el centro de la cuerda, h=0.1

w=1; %velocidad angular de rotación
L=1; %longitud de la cuerda
h=0.1; %deformación
N=50; %número de términos
%coeficientes A_m
A=zeros(1,N);
for m=1:N %inicial
    A(m)=(4*m-1)*2*h*(integral(@(x) legendreP(2*m-1,x/L).*x/L, 0,L/2)+
integral(@(x) legendreP(2*m-1,x/L).*(1-x/L), L/2,L))/L;
end

hold on
x=linspace(0,L,200);
y=zeros(1,length(x));
for m=1:N %inicial
    y=y+A(m)*legendreP(2*m-1,x/L);
end
plot(x,y,'r');
t=0.5; %instante
y=zeros(1,length(x));
for m=1:N 
    y=y+A(m)*legendreP(2*m-1,x/L)*cos(w*sqrt(m*(2*m-1))*t);
end
plot(x,y,'b');
hold off
grid on
legend('0','0.5')
xlabel('x')
ylabel('\Psi(x,t)')
title('Vibraciones de una cuerda en rotación')

Referencias

N. S. Kosholyakov, M. M. Smirnov, E. B. Gliner. Differential equations of Mathematical Physics. North-Holland Publishing Company (1964) pp. 210-213

Lim Yung-kuo. Problems and Solutions on Mechanics. World Scientific (1994). Problem 1232, pp. 379-382