Ecuación diferencial del movimiento ondulatorio

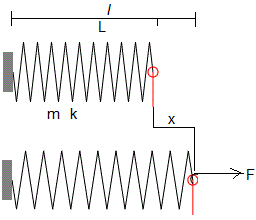
Un muelle elástico se comporta de forma análoga a una barra elástica, deduciremos de forma similar la ecuación diferencial del movimiento ondulatorio y determinaremos la velocidad de propagación de las ondas longitudinales

Sea un muelle elástico de longitud L sin deformar. Cuando se le aplica una fuerza F a su extremo libre se alarga x, su longitud es l=L+x. La relación lineal fuerza-deformación se expresa

${\displaystyle F=kx=kL\frac{l-L}{L}}$

Consideremos un elemento diferencial dx del muelle en la posición x. A causa de la perturbación, el elemento se desplaza u y se deforma du, de modo que la nueva anchura del elemento es dx+du. Calculamos la fuerza necesaria para producir esta deformación

${\displaystyle F=kL\frac{dx+du-dx}{dx}F=kL\frac{\partial u}{\partial x}}$

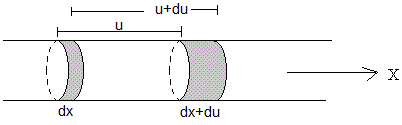
A efectos de notación (derivada parcial) recuérdese que el desplazamiento u, es una función de dos variables x (posición) y t (tiempo).

Desplazamiento del elemento diferencial

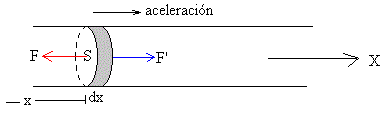
La parte izquierda del muelle ejerce una fuerza F sobre el elemento diferencial de anchura dx, la parte derecha, ejerce una fuerza F' sobre dicho elemento. La fuerza neta es

${\displaystyle F\text{'}-F=dF=kL\frac{{\partial }^{2}u}{\partial x^2}dx}$

La segunda ley de Newton afirma que la fuerza sobre dicho elemento es igual al producto de su masa (m·dx/L) por la aceleración (derivada segunda del desplazamiento)

${\displaystyle dF=\left(\frac{m}{L}dx\right)\frac{{\partial }^{2}u}{\partial t^2}}$

Igualando ambas expresiones obtenemos la ecuación diferencial de un movimiento ondulatorio

${\displaystyle \begin{array}{l}\frac{{\partial }^{2}u}{\partial t^2}=\left(\frac{k{L}^2}{m}\right)\frac{{\partial }^{2}u}{\partial x^2}\\ \frac{{\partial }^{2}u}{\partial t^2}={\omega }^2{L}^2\frac{{\partial }^{2}u}{\partial x^2}\omega =\sqrt{\frac{k}{m}}\end{array}}$

La velocidad de propagación es v=ωL depende de

• k es la constante elástica del muelle
• L es la longitud del muelle sin deformar
• m es la masa del muelle

Condiciones iniciales y de contorno

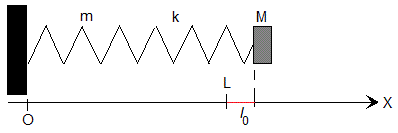
Sea un cuerpo de masa M unido a un muelle elástico de constante k, masa m y longitud L sin deformar

• Las condiciones iniciales son

En el instante t=0, el muelle está en reposo

${\displaystyle {\frac{\partial (u,t)}{\partial t}|}_{t=0}=0}$

Se ha deformado l₀, por lo que un punto x del muelle se ha desplazado u(x,0)=xl₀/L

• Las condiciones de contorno son

El extremo izquierdo del muelle está fijo, u(0,t)=0

La fuerza F que ejerce el muelle sobre el cuerpo de masa M, produce una aceleración

${\displaystyle \begin{array}{l}-kL{\frac{\partial u(x,t)}{\partial x}|}_{x=L}=M{\frac{{\partial }^{2}u(x,t)}{\partial t^2}|}_{x=L}\\ {\frac{\partial u(x,t)}{\partial x}|}_{x=L}=-\frac{M}{kL}\left(\frac{k{L}^2}{m}\right){\frac{{\partial }^{2}u(x,t)}{\partial x^2}|}_{x=L}\\ {\frac{\partial u(x,t)}{\partial x}|}_{x=L}=-\frac{ML}{m}{\frac{{\partial }^{2}u(x,t)}{\partial x^2}|}_{x=L}\end{array}}$

Separación de variables

Para resolver la ecuación diferencial dividimos la solución en producto de dos funciones una dependiente de x y la otra de t.

${\displaystyle \begin{array}{l}u(x,t)=X(x)·T(t)\hfill \\ \frac{1}{T(t)}\frac{d^{2}T}{d{t}^2}={\omega }^2{L}^2\frac{1}{X(x)}\frac{d^{2}X}{d{x}^2}=-{\omega }^2{\xi }^2\hfill \end{array}}$

Como el miembro izquierdo depende solamente de t y el derecho solamente de x, entonces, igualamos ambos a una constante que denominaremos -(ωξ)². Obtenemos el sistema de dos ecuaciones diferenciales

${\displaystyle \{\begin{array}{l}\frac{d^{2}T}{d{t}^2}+{\xi }^2{\omega }^2·T=0\\ \frac{d^{2}X}{d{x}^2}+\frac{{\xi }^2}{L^2}X=0\end{array}}$

Ambas ecuaciones tienen soluciones conocidas

${\displaystyle \begin{array}{l}T(t)=A\cos (\xi \omega t)+B\sin (\xi \omega t)\hfill \\ X(x)=C\cos \left(\xi \frac{x}{L}\right)+D\sin \left(\xi \frac{x}{L}\right)\hfill \end{array}}$

Donde A, B, C y D se determinan a partir de las dos condiciones iniciales y las otras dos de contorno.

Modos de vibración

• Si el muelle está fijo por el extremo izquierdo x=0, entonces X(0)=0 y C=0.

• El muelle está inicialmente en reposo

${\displaystyle \begin{array}{l}{\frac{\partial (u,t)}{\partial t}|}_{t=0}=0\\ {\frac{\partial T(t)}{\partial t}|}_{t=0}=0\end{array}}$

por lo que B=0

• El cuerpo de masa M situado en x=L experimenta una aceleración debido a la fuerza que ejerce el muelle

${\displaystyle \begin{array}{l}{\frac{\partial u(x,t)}{\partial x}|}_{x=L}=-\frac{ML}{m}{\frac{{\partial }^{2}u(x,t)}{\partial x^2}|}_{x=L}\\ \frac{\xi }{L}D\cos \left(\frac{\xi }{L}L\right)=\frac{ML}{m}\frac{{\xi }^2}{L^2}D\sin \left(\frac{\xi }{L}L\right)\\ \cot \left(\xi \right)=\frac{M}{m}\xi \end{array}}$

Se representa la función y=cot(x), y la recta y=x/(m/M), con x=ξ. La intersección son las raíces buscadas. Una ecuación similar calcula los máximos secundarios de difracción de una rendija

m_M=1; %cociente m/M
hold on
fplot(@(x) cot(x),[0,4*pi])
fplot(@(x) x/m_M,[0,4*pi])
hold off
set(gca,'XTick',0:pi/2:4*pi)
set(gca,'XTickLabel',{'0','\pi/2','\pi','3\pi/2','2\pi',
'5\pi/2','3\pi','7\pi/2','4\pi'})
grid on
ylim([-20,20])
xlabel('\lambda/\omega')
ylabel('y')
title('Raíces')

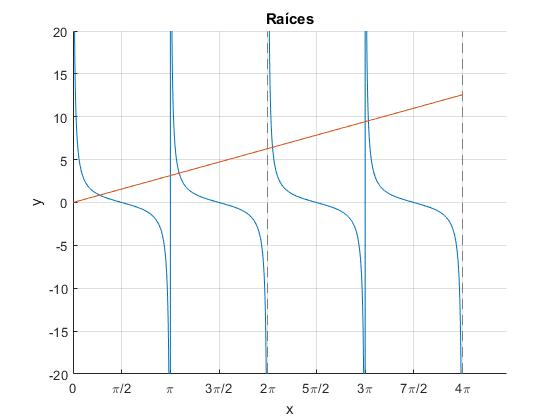
Las raíces están en los intervalos (0,π/2), (π,3π/2), (2π,5π/2)....La función cot(nπ) se hace infinita, para n=0,1,2,3...Cuando se aplican el procedimiento numérico fzero de MATLAB, aparece un error que podemos de evitar calculando las raíces de la ecuación transcendente equivalente

${\displaystyle \frac{m}{M}\cos \left(\xi \right)-\xi \sin \left(\xi \right)=0}$

Los primeros valores de las raíces de la ecuación transcendente para m/M=1, son

m_M=1; %cociente m/M
f=@(x) m_M*cos(x)-x*sin(x);
for n=0:5
    xi_n=fzero(f,[n*pi,n*pi+pi/2]);
    disp(xi_n)
end

    0.8603
    3.4256
    6.4373
    9.5293
   12.6453
   15.7713

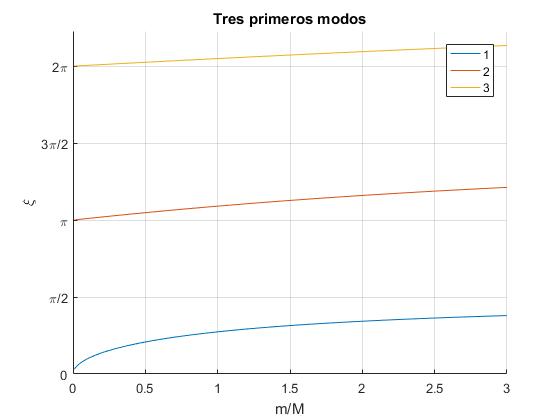
Cuando m/M→0, cot(ξ)→∞, las raíces ξ_n se aproximan a 0, π, 2π...

Cuando n es grande las raíces ξ_n se aproximan a (n-1)π

En al figura, observamos cómo cambia ξ₁, ξ₂ y ξ₃ con el cociente m/M

m_M=0.01:0.01:3; %cociente m/M
xi=zeros(1,length(m_M));
hold on
for n=0:2
    i=1;
    for c=m_M
        f=@(x) c*cos(x)-x*sin(x);
        xi(i)=fzero(f,[n*pi,n*pi+pi/2]);
       i=i+1;
    end
    plot(m_M,xi, 'displayName',num2str(n+1))
end
hold off
set(gca,'YTick',0:pi/2:4*pi)
set(gca,'YTickLabel',{'0','\pi/2','\pi','3\pi/2','2\pi','5\pi/2',
'3\pi','7\pi/2','4\pi'})
legend('-DynamicLegend','location','northeast')
grid on
ylabel('\lambda/\omega')
xlabel('m/M')
title('Tres primeros modos')

La solución de la ecuación diferencial correspondiente al modo n, con B=0 y C=0 es

${\displaystyle u_n(x,t)=X_n(x)T_n(t)=\sin \left({\xi }_n\frac{x}{L}\right)A_n\cos ({\xi }_n\omega t)}$

Superposición

La solución general, es la superposición

${\displaystyle u(x,t)={\displaystyle \sum _{n=1}^{\infty }{u}_n(x,t)}={\displaystyle \sum _{n=1}^{\infty }{A}_n\sin \left({\xi }_n\frac{x}{L}\right)\cos ({\xi }_n\omega t)}}$

Para calcular los coeficientes A_n, utilizamos los siguientes relaciones de las funcione seno y coseno.

${\displaystyle \begin{array}{l}\sin A\sin B=\frac{\cos (A-B)-\cos (A+B)}{2}\\ \cos A\cos B=\frac{\cos (A-B)+\cos (A+B)}{2}\end{array}}$

para calcular las integrales siguientes

${\displaystyle {\displaystyle \underset{0}{\overset{L}{\int }}\sin \left({\xi }_n\frac{x}{L}\right)\sin \left({\xi }_m\frac{x}{L}\right)dx}=L\frac{\sin \left({\xi }_n\right)\cos \left({\xi }_m\right)\left({\xi }_m-{\xi }_n\frac{\tan \left({\xi }_m\right)}{\tan \left({\xi }_n\right)}\right)}{\left({\xi }_n-{\xi }_m\right)\left({\xi }_n+{\xi }_m\right)}}$

Teniendo en cuenta que que ξ_n son las raíces de la ecuación transcendente,

${\displaystyle \begin{array}{l}\tan \left({\xi }_i\right)=\frac{m}{M{\xi }_i}i=m,n\\ {\displaystyle \underset{0}{\overset{L}{\int }}\sin \left({\xi }_n\frac{x}{L}\right)\sin \left({\xi }_m\frac{x}{L}\right)dx}=-\frac{L}{{\xi }_m}\sin \left({\xi }_n\right)\cos \left({\xi }_m\right)=\\ -\frac{ML}{m}\sin \left({\xi }_n\right)\sin \left({\xi }_m\right)m\ne n\end{array}}$

Del mismo modo

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{L}{\int }}\cos \left({\xi }_n\frac{x}{L}\right)\cos \left({\xi }_m\frac{x}{L}\right)dx}=L\frac{\sin \left({\xi }_n\right)\sin \left({\xi }_m\right)\left({\xi }_n-{\xi }_m\frac{\tan \left({\xi }_m\right)}{\tan \left({\xi }_n\right)}\right)}{\left({\xi }_n-{\xi }_m\right)\left({\xi }_n+{\xi }_m\right)}=\\ L\frac{\sin \left({\xi }_n\right)\sin \left({\xi }_m\right)\left({\xi }_n-{\xi }_n\right)}{\left({\xi }_n-{\xi }_m\right)\left({\xi }_n+{\xi }_m\right)}=0m\ne n\end{array}}$

Este es un resultado importante, que nos dice que las funciones cos(ξ_nx/L) son ortogonales pero no lo son las funciones seno

Cuando los índices m y n son iguales, utilizamos las relaciones trigonométricas

${\displaystyle \begin{array}{l}{\sin }^{2}A=\frac{1}{2}\left(1-\cos \left(2A\right)\right)\\ {\cos }^{2}A=\frac{1}{2}\left(1+\cos \left(2A\right)\right)\end{array}}$

para calcular las integrales

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{L}{\int }}{\sin }^2\left({\xi }_n\frac{x}{L}\right)dx}=\frac{L}{2}\left(1-\frac{M}{m}{\sin }^2\left({\xi }_n\right)\right)\\ {\displaystyle \underset{0}{\overset{L}{\int }}{\cos }^2\left({\xi }_n\frac{x}{L}\right)dx}=\frac{L}{2}\left(1+\frac{M}{m}{\sin }^2\left({\xi }_n\right)\right)\end{array}}$

La deformación inicial del muelle es l₀ o bien, u(x,0)=xl₀/L, nos permite calcular los coeficientes A_n

${\displaystyle x\frac{l_0}{L}={\displaystyle \sum _{n=1}^{\infty }{A}_n\sin \left({\xi }_n\frac{x}{L}\right)}}$

Sin embargo, las funciones seno no son ortogonales, por lo que tendremos que utilizar las funciones coseno, por lo que procedemos a derivar ambos miembros

${\displaystyle l_0={\displaystyle \sum _{n=1}^{\infty }{A}_n{\xi }_n\cos \left({\xi }_n\frac{x}{L}\right)}}$

Multiplicamos ambos miembros por cos(ξ_mx/L) en integramos entre 0 y L

${\displaystyle \begin{array}{l}{l}_0{\displaystyle \underset{0}{\overset{L}{\int }}\cos \left({\xi }_n\frac{x}{L}\right)}dx={\displaystyle \sum _{m=1}^{\infty }{A}_m{\xi }_m{\displaystyle \underset{0}{\overset{L}{\int }}\cos \left({\xi }_m\frac{x}{L}\right)}}\cos \left({\xi }_n\frac{x}{L}\right)dx\\ l_0\frac{L}{{\xi }_n}\sin \left({\xi }_n\right)={\xi }_n{A}_n\frac{L}{2}\left(1+\frac{M}{m}{\sin }^2\left({\xi }_n\right)\right)\\ A_n=2l_0\frac{1}{{\xi }_n^2}\frac{\sin \left({\xi }_n\right)}{1+\frac{M}{m}{\sin }^2\left({\xi }_n\right)}\end{array}}$

Cuando x=L, se cumplirá que

${\displaystyle {\displaystyle \sum _{n=1}^{\infty }\frac{1}{{\xi }_n^2}\frac{{\sin }^2\left({\xi }_n\right)}{1+\frac{M}{m}{\sin }^2\left({\xi }_n\right)}}=\frac{1}{2}}$

Resultado importante, que utilizaremos en el cálculo de la energía del sistema. Comprobamos que la suma de la serie tiende hacia 1/2. Tomamos el cociente entre masas m/M=0.3 y se han sumado los 10 primeros términos del desarrollo en serie

m_M=0.3; %cociente m/M
f=@(x) m_M*cos(x)-x*sin(x);
sum=0;
for n=0:10
    xi=fzero(f,[n*pi,n*pi+pi/2]);
    sum=sum+sin(xi)^2/(xi^2*(1+sin(xi)^2/m_M));
end
disp(sum)

    0.5000

La solución completa es

${\displaystyle u(x,t)={\displaystyle \sum _{n=1}^{\infty }{u}_n(x,t)}=2l_0{\displaystyle \sum _{n=1}^{\infty }\frac{1}{{\xi }_n^2}\frac{\sin \left({\xi }_n\right)}{1+\frac{M}{m}{\sin }^2\left({\xi }_n\right)}\sin \left({\xi }_n\frac{x}{L}\right)\cos ({\xi }_n\omega t)}}$

u(x,t) es el desplazamiento de un elemento infinitesimal dx cuya abscisa es x en el muelle no deformado

Energías

Tenemos que calcular tres energías: la energía cinética E_kM del cuerpo de masa M, la energía cinética de los distintos elementos del muelle E_km y su energía potencial E_p, debido a que el muelle experiementa deformaciones. La suma de las tres energías deberá dar constante e igual a la energía inicial del muelle deformado, l₀

${\displaystyle E=E_{km}+E_{kM}+E_P=\frac{1}{2}k{l}_0^2}$

Energía cinética del muelle

El elemento diferencial comprendido entre x yx+dx tiene una masa m·dx/L y se desplaza con velocidad $\frac{\partial u(x,t)}{\partial t}$, su energía cinética es $\frac{1}{2}\left(\frac{m}{L}dx\right){\left(\frac{\partial u(x,t)}{\partial t}\right)}^2$, y la energía cinética total se obtiene integrando con respecto de x en el intervalo 0≤x≤L

${\displaystyle E_{km}={\displaystyle \underset{0}{\overset{L}{\int }}\frac{1}{2}\frac{m}{L}{\left(\frac{\partial u(x,t)}{\partial t}\right)}^2}dx}$

Energía cinética del cuerpo

La energía cinética del cuerpo de masa M situado en x=L, unido al muelle elástico es

${\displaystyle E_{kM}=\frac{1}{2}M{\left(\frac{\partial u(L,t)}{\partial t}\right)}^2}$

Energía potencial del muelle deformado

Cada elemento diferencial comprendido entre x y x+dx, acumula una energía potencial debido a la deformación, que es igual al producto de la fuerza media por el desplazamiento. La fuerza en la posición x, es

${\displaystyle F=kL\frac{\partial u(x,t)}{\partial x}}$

La energía potencial de dicho elemento diferencial

${\displaystyle d{E}_p=\frac{1}{2}kL\frac{\partial u(x,t)}{\partial x}du=\frac{1}{2}kL·{\left(\frac{\partial u(x,t)}{\partial x}\right)}^{2}dx}$

La energía potencial total se obtiene, integrando con respecto de x en el intervalo 0≤x≤L

${\displaystyle E_p={\displaystyle \underset{0}{\overset{L}{\int }}\frac{1}{2}kL{\left(\frac{\partial u(x,t)}{\partial x}\right)}^{2}dx}}$

Energía del modo n de vibración

Dado que u(x,t) es la superposición de los infinitos modos de vibración, calculamos la energía de cada uno de los modos

${\displaystyle \begin{array}{l}u(x,t)={\displaystyle \sum _{n=1}^{\infty }{u}_n(x,t)}\\ u_n(x,t)=A_n\sin \left({\xi }_n\frac{x}{L}\right)\cos ({\xi }_n\omega t)\end{array}}$

Calculamos la energía total para el modo n y sumamos para todos los modos. La energía total deberá ser constante e igual a la energía de deformación inicial del muelle elástico

• Energía cinética del muelle elástico

${\displaystyle \begin{array}{l}{\left(E_{km}\right)}_n={\displaystyle \underset{0}{\overset{L}{\int }}\frac{1}{2}\frac{m}{L}{\left(\frac{\partial u_n(x,t)}{\partial t}\right)}^2}dx=\frac{1}{2}\frac{m}{L}{A}_n^2{\xi }_n^2{\omega }^2{\sin }^2\left({\xi }_n\omega t\right){\displaystyle \underset{0}{\overset{L}{\int }}{\sin }^2\left({\xi }_n\frac{x}{L}\right)dx}=\\ \frac{1}{4}m{A}_n^2{\xi }_n^2{\omega }^2\left(1-\frac{M}{m}{\sin }^2\left({\xi }_n\right)\right){\sin }^2\left({\xi }_n\omega t\right)\end{array}}$

• Energía cinética del cuerpo de masa M

${\displaystyle {\left(E_{kM}\right)}_n=\frac{1}{2}M{\left(\frac{\partial u_n(L,t)}{\partial t}\right)}^2=\frac{1}{2}M{A}_n^2{\xi }_n^2{\omega }^2{\sin }^2\left({\xi }_n\right){\sin }^2\left({\xi }_n\omega t\right)}$

• Energía potencial del muelle elástico

${\displaystyle \begin{array}{l}{\left(E_p\right)}_n={\displaystyle \underset{0}{\overset{L}{\int }}\frac{1}{2}kL{\left(\frac{\partial u_n(x,t)}{\partial x}\right)}^{2}dx}=\frac{1}{2}kL{A}_n^2\frac{{\xi }_n^2}{L^2}{\cos }^2\left({\xi }_n\omega t\right){\displaystyle \underset{0}{\overset{L}{\int }}{\cos }^2\left({\xi }_n\frac{x}{L}\right)dx}=\\ \frac{1}{4}m{A}_n^2{\xi }_n^2{\omega }^2\left(1+\frac{M}{m}{\sin }^2\left({\xi }_n\right)\right){\cos }^2\left({\xi }_n\omega t\right)\end{array}}$

Sumamos los tres términos

${\displaystyle \begin{array}{l}{E}_n={\left(E_{km}\right)}_n+{\left(E_{kM}\right)}_n+{\left(E_p\right)}_n=\\ \frac{1}{4}m{A}_n^2{\xi }_n^2{\omega }^2\left(1-\frac{M}{m}{\sin }^2\left({\xi }_n\right)\right){\sin }^2\left({\xi }_n\omega t\right)+\frac{1}{2}M{A}_n^2{\xi }_n^2{\omega }^2{\sin }^2\left({\xi }_n\right){\sin }^2\left({\xi }_n\omega t\right)+\\ \frac{1}{4}m{A}_n^2{\xi }_n^2{\omega }^2\left(1+\frac{M}{m}{\sin }^2\left({\xi }_n\right)\right){\cos }^2\left({\xi }_n\omega t\right)=\\ \frac{1}{4}{A}_n^2{\xi }_n^2{\omega }^2\left(m+M{\sin }^2\left({\xi }_n\right)\right)\end{array}}$

Teniendo en cuenta la expresión de A_n

${\displaystyle \begin{array}{l}{E}_n=\frac{1}{4}{\left(2\frac{l_0}{{\xi }_n^2}\frac{\sin \left({\xi }_n\right)}{1+\frac{M}{m}{\sin }^2\left({\xi }_n\right)}\right)}^2{\xi }_n^2{\omega }^2\left(m+M{\sin }^2\left({\xi }_n\right)\right)=\\ =m\frac{l_0^2{\omega }^2}{{\xi }_n^2}\frac{{\sin }^2\left({\xi }_n\right)}{1+\frac{M}{m}{\sin }^2\left({\xi }_n\right)}=k\frac{l_0^2}{{\xi }_n^2}\frac{{\sin }^2\left({\xi }_n\right)}{1+\frac{M}{m}{\sin }^2\left({\xi }_n\right)}\end{array}}$

Energía total de todos los modos de vibración

${\displaystyle E={\displaystyle \sum _{n=1}^{\infty }{E}_n}=k{l}_0^2{\displaystyle \sum _{n=1}^{\infty }\frac{{\sin }^2\left({\xi }_n\right)}{{\xi }_n^2\left(1+\frac{M}{m}{\sin }^2\left({\xi }_n\right)\right)}}=\frac{1}{2}k{l}_0^2}$

Hemos utilizado la propiedad importante deducida al final del apartado anterior. La energía total es constante e igual a la deformación inicial del muelle

En la figura se muestra la energía de los tres primeros modos de vibración dividida por la energía inicial $\frac{1}{2}k{l}_0^2$ en función del cociente m/M

m_M=0.01:0.01:3; %cociente m/M
E_n=zeros(1,length(m_M));
hold on
for n=0:2
    i=1;
    for c=m_M
        f=@(x) c*cos(x)-x*sin(x);
        xi=fzero(f,[n*pi,n*pi+pi/2]);
        E_n(i)=2*sin(xi)^2/(xi^2*(1+sin(xi)^2/c)); %E_n/(kl0^2/2)
        i=i+1;
    end
    plot(m_M,E_n, 'displayName',num2str(n+1))
end
hold off
legend('-DynamicLegend','location','northwest')
grid on
ylabel('E_n')
xlabel('m/M')
title('Energía, tres primeros modos')

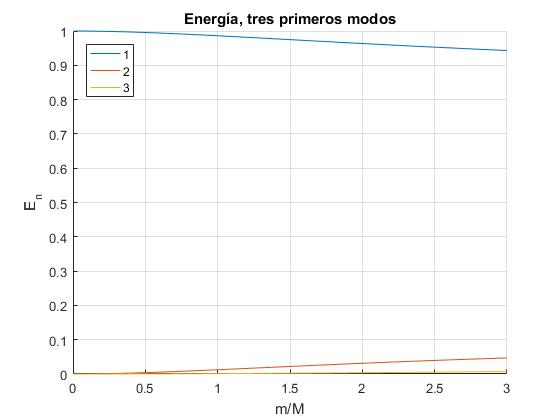
Vemos que el primer modo lleva casi toda la energía cuando el cociente m/M es pequeño

Periodo

En el caso de un muelle ideal de constante k ideal (de masa despreciable) unido a un cuerpo de masa M, el periodo P es

${\displaystyle P=2\pi \sqrt{\frac{M}{k}}}$

Midiendo los periodos P de muelles de constante k y masa m no despreciable, unidos a un cuerpo de masa M se llega a la fórmula

${\displaystyle P=2\pi \sqrt{\frac{M+\frac{m}{f}}{k}}}$

M+m/f es la masa equivalente del sistema y f es un factor del orden de 3

Consideremos el primer modo de vibración

${\displaystyle u_1(x,t)=A_1\sin \left({\xi }_1\frac{x}{L}\right)\cos ({\xi }_1\omega t)}$

Cada punto x del muelle describe un MAS de frecuencia angular ξ₁ω o periodo P₁=2π/(ξ₁ω)

${\displaystyle {\xi }_1^2{\omega }^2=\frac{k}{M+m/f}}$

Como k=mω², despejamos el factor f de dicha ecuación

${\displaystyle \begin{array}{l}{\xi }_1^2=\frac{m}{M+\frac{m}{f}}\\ f=\frac{\left(m/M\right){\xi }_1^2}{\left(m/M\right)-{\xi }_1^2}\end{array}}$

En la figura, representamos el factor f en función del cociente de masas m/M, para el primer modo de vibración, ξ₁

m_M=0.01:0.01:3; %cociente m/M
factor=zeros(1,length(m_M));
hold on
n=0; %primer modo
i=1;
for c=m_M
    f=@(x) c*cos(x)-x*sin(x);
     xi=fzero(f,[n*pi+delta,n*pi+pi/2]);
     factor(i)=c/(c/xi^2-1);
     i=i+1;
end
plot(m_M,factor)
hold off
grid on
ylabel('f')
xlabel('m/M')
title('factor masa añadida')

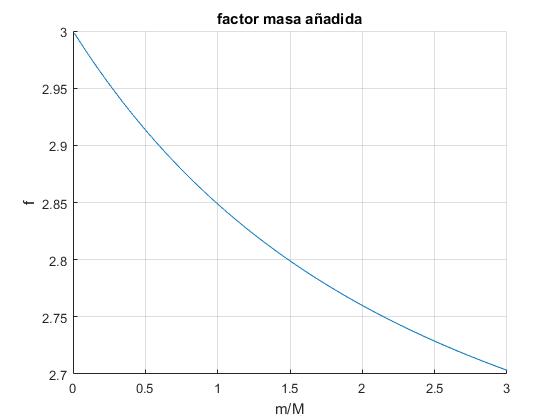
Cuando m/M→0, ξ₁→0, véase la segunda figura titulada 'Tres primeros modos'. Llamemos x=m/M, e y=ξ₁. La ecuación transcendente que relaciona ambas variables, se escribe tan(y)=x/y, por lo que f es

${\displaystyle f=\frac{y^2\tan (y)}{\tan (y)-y}}$

>> syms y;
>> limit(y^2*tan(y)/(tan(y)-y),y,0)
ans =3

Por tanto, cuando m/M→0, f→3

El factor f va disminuyendo a medida que se incrementa el cociente m/M. Cuando m/M→∞, ξ₁→π/2 (véase la segunda figura titulada 'Tres primeros modos'), el factor f→(π/2)²=2.467

Se comprime un muelle y se suelta

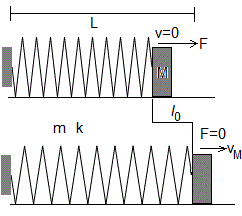
Un muelle de longitud L sin deformar, de masa m y constante elástica k, se comprime l₀ con un cuerpo de masa M. Se suelta en el instante t=0. Vamos a calcular la velocidad del cuerpo cuando el muelle recupera su longitud inicial, x=L. La fuerza que ejerce el muelle sobre el cuerpo será nula

Supondremos que el cuerpo desliza sobre el plano horizontal sin rozamiento

${\displaystyle u(x,t)=-2l_0{\displaystyle \sum _{n=1}^{\infty }\frac{1}{{\xi }_n^2}\frac{\sin \left({\xi }_n\right)}{1+\frac{M}{m}{\sin }^2\left({\xi }_n\right)}\sin \left({\xi }_n\frac{x}{L}\right)\cos ({\xi }_n\omega t)}}$

Donde ξ_n son las raíces de la ecuación transcendente, (m/M)cos(ξ)-ξsin(ξ)=0 y $\omega =\sqrt{\frac{k}{m}}$

La fuerza F que ejerce el muelle elástico en sobre el cuerpo en x=L se hace nula en el instante T.

${\displaystyle F=-kL{\frac{\partial u(x,t)}{\partial x}|}_{x=L}=2k{l}_0{\displaystyle \sum _{n=1}^{\infty }\frac{1}{{\xi }_n}\frac{\sin \left({\xi }_n\right)\cos \left({\xi }_n\right)}{1+\frac{M}{m}{\sin }^2\left({\xi }_n\right)}\cos \left({\xi }_n\omega t\right)}}$

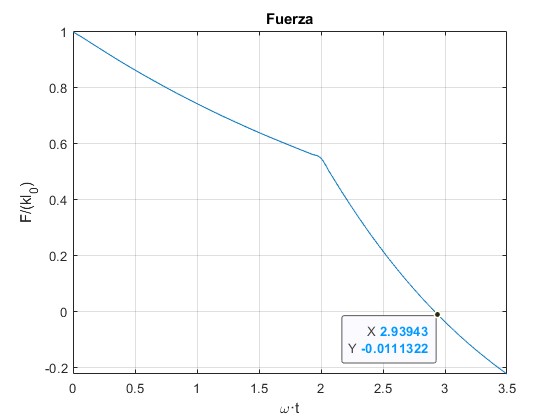
Representamos la fuerza F en x=L en función de ωt, tomando m/M=0.3

function muelle_6
    m_M=0.3; %cociente m/M
    f=@(x) m_M*cos(x)-x*sin(x);
    xn=zeros(1, 20);
    for n=0:length(xn)-1
        xn(n+1)=fzero(f,[n*pi,n*pi+pi/2]);
    end
    function temp=fuerza(t)
         temp=0;
         for k=1:length(xn)
              temp=temp+2*sin(xn(k))*cos(xn(k))*cos(xn(k)*t)/
(xn(k)*(1+sin(xn(k))^2/m_M));
         end
    end
   fplot(@fuerza,[0,3.5])
    grid on
    xlabel('\omega·t')
    ylabel('F/(kl_0)')
    title('Fuerza')
end

Cambiamos m/M=3

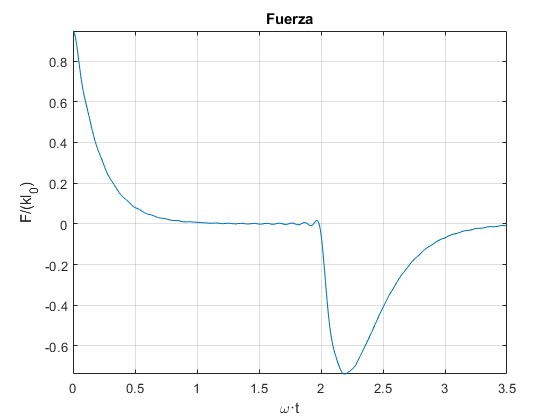
Calculamos el tiempo ωT resolviendo la ecuación transcendente

${\displaystyle {\displaystyle \sum _{n=1}^{\infty }\frac{1}{{\xi }_n}\frac{\sin \left({\xi }_n\right)\cos \left({\xi }_n\right)}{1+\frac{M}{m}{\sin }^2\left({\xi }_n\right)}\cos \left({\xi }_n\omega t\right)}=0}$

Para m/M>2.5, resulta difícil calcular el valor de ωT para el cual la fuerza se anula, tal como se puede apreciar en la segunda representación gráfica de la fuerza, ya que la fuerza es casi tangente al eje de los tiempos

La velocidad v en función del tiempo t es

${\displaystyle v={\frac{\partial u(x,t)}{\partial t}|}_{x=L}=2l_0\omega {\displaystyle \sum _{n=1}^{\infty }\frac{1}{{\xi }_n}\frac{{\sin }^2\left({\xi }_n\right)}{1+\frac{M}{m}{\sin }^2\left({\xi }_n\right)}\sin ({\xi }_n\omega t)}}$

La máxima velocidad v_M del cuerpo se alcanza en el instante t=T. A partir de este instante, el cuerpo de masa M se mueve con dicha velocidad constante

${\displaystyle v_M=2l_0\omega {\displaystyle \sum _{n=1}^{\infty }\frac{1}{{\xi }_n}\frac{{\sin }^2\left({\xi }_n\right)}{1+\frac{M}{m}{\sin }^2\left({\xi }_n\right)}\sin ({\xi }_n\omega T)}}$

Calculamos el tiempo ωT y representamos la velocidad v/(l₀ω) en función de ωt. Calculamos la velocidad v_M máxima del cuerpo

function muelle_5
    m_M=0.3; %cociente m/M
    f=@(x) m_M*cos(x)-x*sin(x);
    xn=zeros(1, 20);
    for n=0:length(xn)-1
        xn(n+1)=fzero(f,[n*pi,n*pi+pi/2]);
    end
    function temp=tiempo(t)
         temp=0;
         for k=1:length(xn)
              temp=temp+sin(xn(k))*cos(xn(k))*cos(xn(k)*t)/
(xn(k)*(1+sin(xn(k))^2/m_M));
         end
    end
      T=fzero(@tiempo,[0,3]);
      disp(T)
     
    function v=velocidad(t)
        v=0;
        for k=1:length(xn)
            v=v+2*sin(xn(k))^2*sin(xn(k)*t)/(xn(k)*
(1+sin(xn(k))^2/m_M));
        end
    end
    fplot(@velocidad,[0,T])
    disp(velocidad(T))
    grid on
    xlabel('\omega•t')
    ylabel('v/(l_0\omega)')
    title('Velocidad')
end

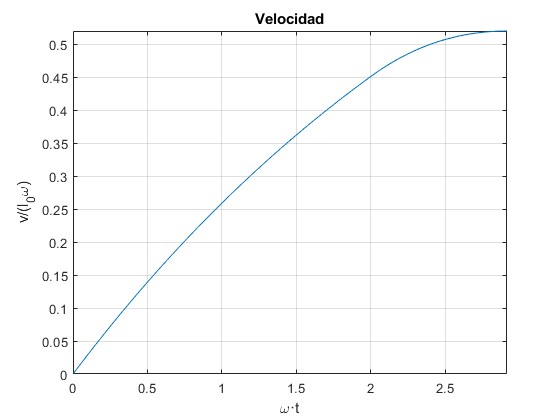
El tiempo ωT=2.9146 y la velocidad del cuerpo es v_M=0.52

   2.9146
   0.5200

Referencias

Ye-Wan Ma, Zhao-Wang Wu, Li-Hua Zhang, Quan-Jin Liu, Xun-Chang Yin, Yong-Cai Shen. Theoretical study of the energy and oscillating period for uniformly distributed mass spring. Eur. J. Phys. 40 (2019) 035004. pp. 1-16.

Vladimir Ivchenko. The internal ballistics of a spring gun. Eur. J. Phys. 45 (2024) 045001