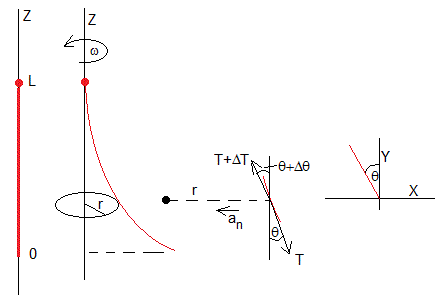
Consideremos una cuerda de longitud L y masa m se sujeta por su extremo superior z=L a un eje vertical que se hace girar con velocidad angular ω.

En la parte izquierda de la figura, la cuerda en reposo, a derecha, la forma de la cuerda cuando el eje gira (se ha exagerado la desviación de la dirección vertical de equilibrio)

Un elemento comprendido entre z y z+Δz de la cuerda de masa mΔz/L describe un movimiento circular de radio r con velocidad angular constante ω. Por tanto, su aceleración en la dirección horizontal es a_n=ω²r, dirigida hacia el centro de la circunferencia que describe.

La componente horizontal de las fuerzas sobre dicho elemento son

${\displaystyle \begin{array}{l}\left(T+\Delta T\right)\sin \left(\theta +\Delta \theta \right)-T\sin \theta =\left(\frac{m}{L}\Delta z\right){\omega }^{2}r\\ \Delta \left(T\sin \theta \right)=\left(\frac{m}{L}\Delta z\right){\omega }^{2}r\end{array}}$

Si la desviación de la cuerda respecto del eje vertical, no es muy grande hacemos la aproximación sinθ≈tanθ

${\displaystyle \Delta \left(T\tan \theta \right)=\left(\frac{m}{L}\Delta z\right){\omega }^{2}r}$

Relacionamos el ángulo θ con la pendiente de la recta tangente a la cuerda dr/dz en el punto de abscisa r y ordenada z

${\displaystyle \begin{array}{l}\tan \theta =-\frac{dr}{dz}\\ -\Delta \left(T\frac{dr}{dz}\right)=\frac{m}{L}{\omega }^{2}r·\Delta z\end{array}}$

La tensión T de la cuerda en z es esencialmente el peso mgz/L de la parte de la cuerda que cuelga, siempre que la velocidad angular ω no sea muy grande.

En el límite, cuando Δz→0, obtenemos la ecuación diferencial

${\displaystyle \begin{array}{l}-\frac{d}{dz}\left(\frac{m}{L}gz\frac{dr}{dz}\right)dz=\frac{m}{L}{\omega }^2·r·dz\\ z\frac{d^{2}r}{d{z}^2}+\frac{dr}{dz}+\frac{{\omega }^2}{g}r=0\end{array}}$

Haciendo la sustitución,

${\displaystyle \begin{array}{l}x=2\omega \sqrt{\frac{z}{g}}\\ \frac{dr}{dz}=\frac{2{\omega }^2}{gx}\frac{dr}{dx}\\ \frac{d^{2}r}{d{z}^2}=\frac{4{\omega }^4}{g^2{x}^2}\frac{d^{2}r}{d{x}^2}-\frac{4{\omega }^4}{g^2{x}^3}\frac{dr}{dx}\\ \frac{d^{2}r}{d{x}^2}+\frac{1}{x}\frac{dr}{dx}+r=0\end{array}}$

transformamos esta ecuación diferencial en la ecuación de Bessel de orden cero

${\displaystyle x^2\frac{d^{2}r}{d{x}^2}+x\frac{dr}{dx}+x^{2}r=0}$

Su solución es

r=A·J₀(x)+B·Y₀(x)

Sujeta por el extremo superior

La solución para este caso es, r=A·J₀(x), ya que Y₀(x)→-∞, cuando x→0

Dado que el punto de suspensión z=L, está fijo, r(L)=0, los posibles modos son las raíces ξ_n de la ecuación J₀(ξ)=0

${\displaystyle \begin{array}{l}2{\omega }_n\sqrt{\frac{L}{g}}={\xi }_n\\ {\omega }_n=\frac{1}{2}{\xi }_n\sqrt{\frac{g}{L}}\end{array}}$

Obtenemos las raíces de la ecuación transcendente utilizando la función, raices, que se ha definido en la página titulada Funciones MATLAB para calcular las raíces de una ecuación

L=1; %longitud
x=linspace(1,25,50);
disp('Velocidades angulares de rotación')
w=raices(@(x) besselj(0,x),x)*sqrt(9.8/L)/2;
disp(w')

En la ventana de comandos obtenemos las velocidades angulares de rotación que corresponden a los sucesivos modos normales.

Velocidades angulares de rotación
    3.7641
    8.6403
   13.5452
   18.4567
   23.3706
   28.2857
   33.2015
   38.1176

La función que describe la forma de la cuerda cuando gira con velocidad angular ω_n es

${\displaystyle r(z)=A·J_0\left(2{\omega }_n\sqrt{\frac{z}{g}}\right)}$

Donde A es un factor de escala

L=1; %longitud
x=linspace(1,25,50);
w=raices(@(x) besselj(0,x),x)*sqrt(9.8/L)/2;

n=2; %segundo modo
fplot(@(x) besselj(0,2*w(n)*sqrt(x/9.8)),[0,1])
grid on
axis equal
view([90 -90])
xlabel('z')
ylabel('r(z)')
title('Rotación')

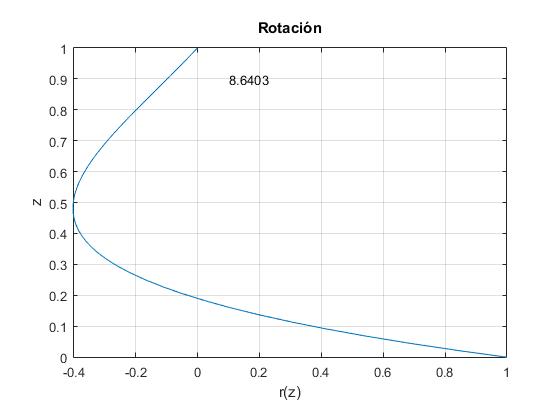
En la figura, vemos el segundo modo n=2, cuya velocidad angular de rotación es 8.64. Cambiando el valor del índice n, representamos distintos modos de rotación del cable.

Actividades

Aparece el primer modo normal de velocidad angular ω₀.

Pulsamos el botón titulado >> y vamos observando los sucesivos modos hasta el quinto.

Pulsamos el botón titulado << y observamos los distintos modos de forma inversa.

La escala horizontal se ha exagerado para apreciar mejor la forma de los distintos modos.

En la parte superior izquierda, se proporcionan los valores de las velocidades angulares ω_n de los distintos modos normales.

Sujeta por ambos extremos

Supongamos un cable de masa M y longitud L suspendido verticalmente. El extremo superior está unido a un eje vertical que gira con velocidad angular ω. El cable está sujeto en el extremo inferior aunque puede girar sin rozamiento alrededor del mismo eje, además, de este extremo pende una carga que hace que el cable esté tenso.

La ecuación diferencial que describe el movimiento de rotación del cable es

${\displaystyle \frac{\partial }{\partial z}\left(T(z)\frac{\partial R(z,t)}{\partial z}\right)=\frac{{\partial }^2}{\partial t^2}\left(\frac{m}{L}R(z,t)\right)}$

En el estado estacionario, buscamos una solución de la forma

${\displaystyle \begin{array}{l}R(z,t)=r(z)·\sin (\omega t)\\ \frac{d}{dz}\left(T(z)\frac{dr(z)}{dz}\right)+{\omega }^2\frac{m}{L}r(z)=0\end{array}}$

T(z) es la tensión vertical del cable, incluyendo su propio peso

${\displaystyle T(z)=T_0+\frac{m}{L}gz}$

T₀ es la tensión adicional que se aplica en el extremo inferior del cable, por ejemplo, colgando una pesa, tal como se muestra en la figura.

Obtenemos la ecuación diferencial

${\displaystyle \left(\frac{T_0}{mg}+\frac{z}{L}\right)\frac{d^{2}r}{d{z}^2}+\frac{1}{L}\frac{dr}{dz}+\frac{{\omega }^2}{gL}r=0}$

Hacemos el cambio de variable, $y=\frac{z}{L}+\frac{T_0}{mg}$ y obtenemos la ecuación diferencial

${\displaystyle y\frac{d^{2}r}{d{y}^2}+\frac{dr}{dy}+\frac{{\omega }^{2}L}{g}r=0}$

Hacemos un nuevo cambio de variable (véase el primer apartado)

${\displaystyle \begin{array}{l}x=2\omega \sqrt{\frac{yL}{g}}\\ \frac{dr}{dy}=\frac{2{\omega }^{2}L}{gx}\frac{dr}{dx}\\ \frac{d^{2}r}{d{y}^2}=\frac{4{\omega }^4{L}^2}{g^2{x}^2}\frac{d^{2}r}{d^{2}x}-\frac{4{\omega }^4{L}^2}{g^2{x}^3}\frac{dr}{dx}\\ \frac{d^{2}r}{d{x}^2}+\frac{1}{x}\frac{dr}{dx}+r=0\end{array}}$

transformamos esta ecuación diferencial en la ecuación de Bessel de orden cero

La solución de esta ecuación diferencial es

${\displaystyle \begin{array}{l}r(z)=C_1{J}_0(x)+C_2{Y}_0(x)\\ r(z)=C_1{J}_0\left(2\omega \sqrt{\frac{yL}{g}}\right)+C_2{Y}_0\left(2\omega \sqrt{\frac{yL}{g}}\right)\\ r(z)=C_1{J}_0\left(\frac{2\omega }{g}\sqrt{\frac{L}{m}\left(\frac{m}{L}gz+T_0\right)}\right)+C_2{Y}_0\left(\frac{2\omega }{g}\sqrt{\frac{L}{m}\left(\frac{m}{L}gz+T_0\right)}\right)\end{array}}$

J₀ e Y₀ son las funciones de Bessel de orden cero de primera y segunda especie.

Las condiciones de contorno r(0)=r(L)=0, el cable sujeto por ambos extremos, proporcionan dos ecuaciones.

${\displaystyle \begin{array}{l}{C}_1{J}_0\left(\frac{2\omega }{g}\sqrt{\frac{L}{m}{T}_0}\right)+C_2{Y}_0\left(\frac{2\omega }{g}\sqrt{\frac{L}{m}{T}_0}\right)=0\\ C_1{J}_0\left(\frac{2\omega }{g}\sqrt{\frac{L}{m}\left(mg+T_0\right)}\right)+C_2{Y}_0\left(\frac{2\omega }{g}\sqrt{\frac{L}{m}\left(mg+T_0\right)}\right)=0\end{array}}$

Despejando C₁ en la primera ecuación y sustituyéndola en la segunda obtenemos la ecuación trascendente en ω que resolvemos aplicando procedimientos numéricos.

${\displaystyle \begin{array}{l}{J}_0\left(\frac{2\omega }{g}\sqrt{\frac{L}{m}{T}_0}\right)Y_0\left(\frac{2\omega }{g}\sqrt{\frac{L}{m}\left(mg+T_0\right)}\right)-Y_0\left(\frac{2\omega }{g}\sqrt{\frac{L}{m}{T}_0}\right)J_0\left(\frac{2\omega }{g}\sqrt{\frac{L}{m}\left(mg+T_0\right)}\right)=0\\ J_0\left(\gamma \omega \right)Y_0\left(\gamma \omega \sqrt{\frac{mg}{T_0}+1}\right)-Y_0\left(\gamma \omega \right)J_0\left(\gamma \omega \sqrt{\frac{mg}{T_0}+1}\right)=0\gamma =2\sqrt{\frac{L}{g}·\frac{T_0}{mg}}\end{array}}$

Cuyas raíces ω₁, ω₂,… ω_n, nos dan las velocidades angulares de rotación que corresponden a los modos normales.

Llamamos p=Mg/T₀, x=γω. Fijamos la longitud del cable L=1.0, y establecemos el valor de su tensión T₀ de modo que el parámetro p=1.0. Obtenemos las raíces de la ecuación transcendente utilizando la función raices que se ha definido en la página titulada Funciones MATLAB para calcular las raíces de una ecuación

p=1.0; %parámetro
gamma=2*sqrt(1.0/(9.8*p));
f=@(x) besselj(0,x).*bessely(0,x*sqrt(p+1))-
bessely(0,x).*besselj(0,x*sqrt(p+1));
x=linspace(1,100,100);
disp('Velocidades angulares de rotación')
w=raices(f,x)/gamma;
disp(w')

En la ventana de comandos obtenemos las velocidades angulares de rotación que corresponden a los sucesivos modos normales.

número de intervalos:13
Velocidades angulares de rotación
   11.8537
   23.7341
   35.6087
   47.4818
   59.3543
   71.2265
   83.0985
   94.9704
  106.8422
  118.7140
  130.5857
  142.4575
  154.3292

Cambiamos el valor de parámetro p y obtenemos otro conjunto de valores para ω₁, ω₂,… ω_n,

Las distintas configuraciones r_n(z) se obtienen expresando C₂ en términos de C₁, en la primera ecuación del sistema.

${\displaystyle r_n(z)=C_n\left\{J_0\left(\gamma {\omega }_n\sqrt{\frac{mg}{T_0}\frac{z}{L}+1}\right)-\frac{J_0\left(\gamma {\omega }_n\right)}{Y_0\left(\gamma {\omega }_n\right)}{Y}_0\left(\gamma {\omega }_n\sqrt{\frac{mg}{T_0}\frac{z}{L}+1}\right)\right\}}$

La constante C_n se determina haciendo que

${\displaystyle {\displaystyle \underset{0}{\overset{L}{\int }}{r}^2(z)·dz}=1}$

Elaboramos un script que que calcule las velocidades angulares y nos represente los distintos modos normales de rotación del cable

p=1.0; %parámetro
gamma=2*sqrt(1.0/(9.8*p));
f=@(x) besselj(0,x).*bessely(0,x*sqrt(p+1))-
bessely(0,x).*besselj(0,x*sqrt(p+1));
x=linspace(1,100,100);
raiz=raices(f,x);

n=2;  %modo normal
gw=raiz(n);
f=@(x) besselj(0,gw*sqrt(p*x+1))- besselj(0,gw)*
bessely(0,gw*sqrt(p*x+1))/bessely(0,gw);
f2=@(x) f(x).*f(x);
const=integral(f2,0,1.0);  
x=linspace(0,1.0,100);
y=f(x)/sqrt(const);  %normaliza
plot(y,x)
grid on
text(0,0.9, num2str(gw/gamma))
xlabel('x')
ylabel('y')
title('Rotación de un cable')

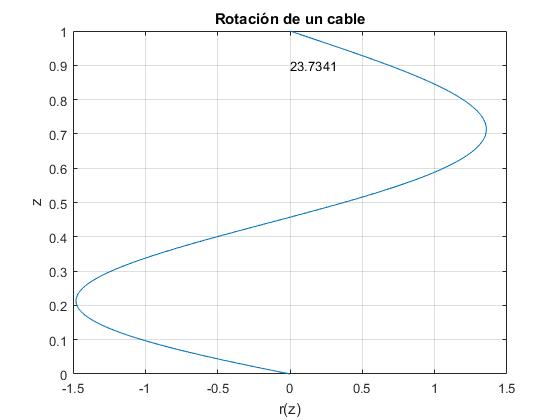
En la figura, vemos el segundo modo n=2, cuya velocidad angular de rotación es 23.73. Cambiando el valor del índice n, representamos distintos modos de rotación del cable.

Actividades

Se introduce

• El valor del parámetro Mg/T₀ en el control titulado Parámetro
• La longitud del cable se ha fijado en L=1 m

Se pulsa el botón titulado Nuevo

Aparece el primer modo normal de velocidad angular ω₀.

Pulsamos el botón titulado >> y vamos observando los sucesivos modos hasta el quinto.

Pulsamos el botón titulado << y observamos los distintos modos de forma inversa.

La escala horizontal se ha exagerado para apreciar mejor la forma de los distintos modos.

En la parte superior derecha, se proporcionan los valores de las velocidades angulares ω_n de los distintos modos normales.

• Cuando la tensión del cable T₀ es mucho mayor que el peso Mg, las funciones r_n(z) son casi simétricas respecto del plano z=L/2.
• Cuando la tensión del cable T₀ es comparable al peso Mg, las funciones r_n(z) son asimétricas.

Referencias

A. B. Western. Demostration for observing J₀(x) on a resonant rotating vertical chain. Am. J. Phys. 48(1) Jan. 1980, pp. 54-56

Noël J-M., Niquette C., Lockridge S., Gauthier N., Natural configurations and normal frequencies of a vertically suspended, spinning, loaded cable with both extremities pinned. Eur. J. Phys. 29 (2008), pp. N47-N5