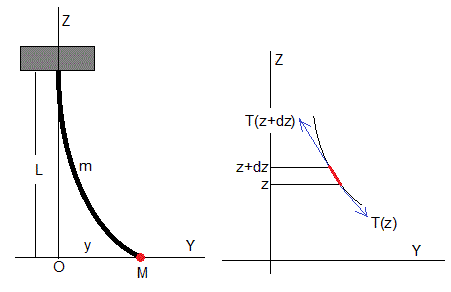
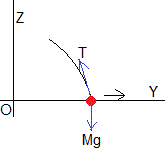
Sea una cuerda suspendida verticalmente, de longitud L y masa m y densidad uniforme m/L que tiene una partícula de masa M en su extremo inferior. El origen y los ejes se muestran en la figura. El punto de suspensión tiene de coordenadas z=L, e y=0.

La deducción de la ecuación del movimiento de un elemento de la cuerda (señalado en color rojo en la figura de la derecha) es similar a la de las ondas transversales en una cuerda, la diferencia es que la tensión de la cuerda es constante y aquí la tensión de la cuerda en la posición z es el peso de la parte de la cuerda por debajo de z.

T(z)=(mz/L)g+Mg

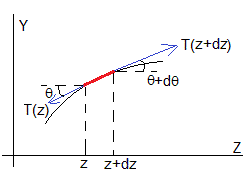
Consideremos una porción de cuerda comprendida entre z y z+dz

• T(z), es la fuerza que ejerce la parte de abajo de la cuerda sobre el elemento diferencial
• T(z+dz), es la fuerza que ejerce la parte de arriba de la cuerda sobre el elemento diferencial

Para deducir la ecuación del movimiento del elemento diferencial de la cuerda giramos los ejes, tal como se muestra en la figura

La componente Y de las fuerzas, dF_y, que actúan sobre dicho elemento diferencial de masa m·dz/L+Mg es

${\displaystyle \begin{array}{l}d{F}_y=T(z+dz)·\sin (\theta +d\theta )-T(z)\sin \theta \simeq \\ \left(T(z)+\frac{dT}{dz}dz\right)·(\sin \theta +\cos \theta ·d\theta )-T(z)\sin \theta =\\ \frac{d}{dz}\left(\sin \theta ·T(z)\right)·dz\simeq \frac{d}{dz}\left(\tan \theta ·T(z)\right)·dz=\frac{d}{dz}\left(\frac{dy}{dz}·T(z)\right)·dz\end{array}}$

Para ángulos pequeños, hacemos la aproximación sinθ≈tanθ

Esta componente dF_y de fuerza sobre el elemento diferencial de masa m·dz/L produce una aceleración a lo largo del eje Y. Teniendo en cuenta que y es una función de z y t, escribimos, la segunda ley de Newton, fuerza=masa×aceleración

${\displaystyle \begin{array}{l}\frac{\partial }{\partial z}\left(\frac{\partial y}{\partial z}T(z)\right)dz=\left(\frac{m}{L}dz\right)\frac{{\partial }^{2}y}{\partial t^2}\hfill \\ \frac{\partial }{\partial z}\left(\frac{\partial y}{\partial z}\left(\frac{m}{L}gz+Mg\right)\right)=\left(\frac{m}{L}\right)\frac{{\partial }^{2}y}{\partial t^2}\hfill \end{array}}$

Separación de variables

Escribimos la solución como producto, y(z,t)=Φ(z)·T(t), lo que nos permite sustituir una ecuación en derivadas particiales por dos ecuaciones diferenciales, una que depende de la variable z y otra de la variable t

${\displaystyle \begin{array}{l}g\frac{d}{dz}\left(\left(z+\frac{M}{m}L\right)\frac{d\Phi }{dz}\right)T=\frac{d^{2}T}{d{t}^2}\Phi \hfill \\ \frac{\frac{d^{2}T}{d{t}^2}}{T}=\frac{g\frac{d}{dz}\left(\left(z+\frac{M}{m}L\right)\frac{d\Phi }{dz}\right)}{\Phi }=-{\omega }^2\hfill \\ \{\begin{array}{l}\frac{d^{2}T}{d{t}^2}+{\omega }^{2}T=0\\ \frac{d}{dz}\left(\left(z+\frac{M}{m}L\right)\frac{d\Phi }{dz}\right)+\frac{{\omega }^2}{g}\Phi =0\end{array}\hfill \end{array}}$

En la segunda ecuación diferencial, hacemos el cambio de variable

${\displaystyle \begin{array}{l}\begin{array}{l}{x}^2=4\left(z+\frac{M}{m}L\right)x=2\sqrt{z+\frac{M}{m}L}\hfill \\ \frac{d\Phi }{dz}=\frac{d\Phi }{dx}\frac{dx}{dz}=\frac{d\Phi }{dx}\frac{2}{x}\hfill \end{array}\hfill \\ \frac{d}{dz}\left(\left(z+\frac{M}{m}L\right)\frac{d\Phi }{dz}\right)=\frac{d}{dz}\left(\frac{x^2}{4}\frac{d\Phi }{dz}\right)=\frac{d}{dx}\left(\frac{x^2}{4}\frac{2}{x}\frac{d\Phi }{dx}\right)\frac{dx}{dz}=\frac{d}{dx}\left(\frac{x}{2}\frac{d\Phi }{dx}\right)\frac{2}{x}=\frac{1}{x}\frac{d\Phi }{dx}+\frac{d^2\Phi }{d{x}^2}\hfill \end{array}}$

Finalmente, llegamos a la ecución diferencial de Bessel con n=0

${\displaystyle x^2\frac{d^2\Phi }{d{x}^2}+x\frac{d\Phi }{dx}+\frac{{\omega }^2}{g}{x}^2\Phi =0}$

La solución de la ecuación diferencial es

${\displaystyle \Phi (x)=A{J}_0\left(\sqrt{\frac{{\omega }^2}{g}}x\right)+B{Y}_0\left(\sqrt{\frac{{\omega }^2}{g}}x\right)}$

Estudiaremos los distintos casos

Modos de vibración de la cuerda que cuelga

Supongamos que se suprime la partícula, M=0, la relación entre las variables es $x=\sqrt{z}$, cuando z→0, x→0

La función Y₀(x) tiende a -∞ cuando x→0. La solución es

${\displaystyle \Phi =A{J}_0\left(\sqrt{\frac{{\omega }^2}{g}}x\right)=A{J}_0\left(2\omega \sqrt{\frac{z}{g}}\right)}$

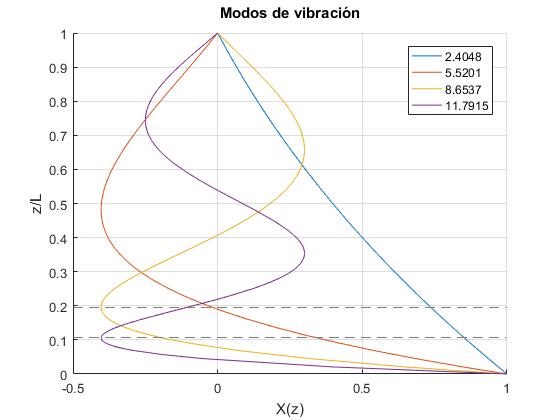
Dado que el punto de suspensión z=L, está fijo, Φ(L)=0, los posibles modos de vibración viene dados por las raíces ξ_n de la ecuación transcendente J₀(ξ)=0

${\displaystyle \begin{array}{l}2{\omega }_n\sqrt{\frac{L}{g}}={\xi }_n\\ {\omega }_n=\frac{1}{2}{\xi }_n\sqrt{\frac{g}{L}}\end{array}}$

Obtenemos las raíces de la ecuación transcendente J₀(ξ)=0, utilizando la función, raices, que se ha definido en la página titulada Funciones MATLAB para calcular las raíces de una ecuación

Representamos los cuatro primeros modos de vibración, con los ejes girados.

${\displaystyle \Phi (z)=A{J}_0\left({\xi }_n\sqrt{\frac{z}{L}}\right)0\le z<L}$

L=1; %longitud
x=linspace(1,12,10);
raiz=raices(@(x) besselj(0,x),x);

hold on
for xi=raiz
    fplot(@(z) besselj(0,xi*sqrt(z/L)), [0,1],'displayName',num2str(xi));
end
hold off
grid on
view([90 -90]) %ejes girados
legend('-DynamicLegend','location','northeast')
xlabel('z/L')
ylabel('X(z)')
title('Modos de vibración')

Modos de vibración de la cuerda con la partícula

En este caso, M≠0, la relación entre las variables es $x=2\sqrt{\left(z+\frac{M}{m}L\right)}$, cuando z→0, $x\to 2\sqrt{\frac{M}{m}L}$

La solución de la ecuación diferencial incluye a J₀(x) e Y₀(x)

${\displaystyle \begin{array}{l}\Phi (x)=A{J}_0\left(\sqrt{\frac{{\omega }^2}{g}}x\right)+B{Y}_0\left(\sqrt{\frac{{\omega }^2}{g}}x\right)\\ \Phi (z)=A{J}_0\left(2\sqrt{\frac{{\omega }^2}{g}\left(z+\frac{M}{m}L\right)}\right)+B{Y}_0\left(2\sqrt{\frac{{\omega }^2}{g}\left(z+\frac{M}{m}L\right)}\right)\end{array}}$

Llamando $\xi =2\omega \sqrt{\frac{L}{g}}$, la solución se expresa

${\displaystyle \Phi (z)=A{J}_0\left(\xi \sqrt{\frac{z}{L}+\frac{M}{m}}\right)+B{Y}_0\left(\xi \sqrt{\frac{z}{L}+\frac{M}{m}}\right)}$

El extremo inferior está fijo

Si el extremos inferior está fijo, las condiciones de contorno son: Φ(0)=0 y Φ(L)=0

Tenemos un sistema homogéno de dos ecuaciones

${\displaystyle \{\begin{array}{l}A{J}_0\left(\xi \sqrt{\frac{M}{m}}\right)+B{Y}_0\left(\xi \sqrt{\frac{M}{m}}\right)=0\\ A{J}_0\left(\xi \sqrt{\left(1+\frac{M}{m}\right)}\right)+B{Y}_0\left(\xi \sqrt{\left(1+\frac{M}{m}\right)}\right)=0\end{array}}$

Despejamos B en la primera y sustituímos en la segunda.

${\displaystyle J_0\left(\sqrt{\frac{M}{m}}\xi \right)Y_0\left(\sqrt{1+\frac{M}{m}}\xi \right)-Y_0\left(\sqrt{\frac{M}{m}}\xi \right)J_0\left(\sqrt{1+\frac{M}{m}}\xi \right)=0}$

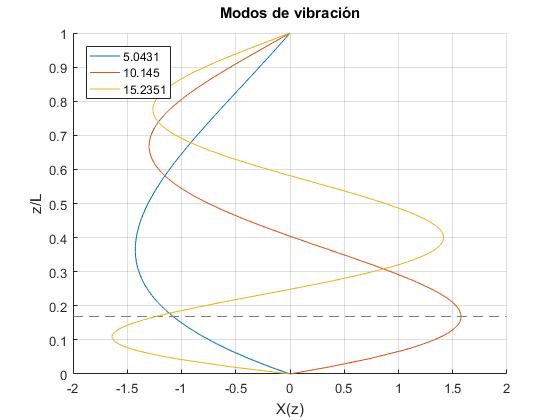
Calculamos las raíces de la ecuación transcendente, dado el cociente M/m y representamos Φ(z)

${\displaystyle \begin{array}{l}\Phi (z)=A{J}_0\left(\xi \sqrt{\frac{z}{L}+\frac{M}{m}}\right)+B{Y}_0\left(\xi \sqrt{\frac{z}{L}+\frac{M}{m}}\right)=\\ A\left\{J_0\left(\xi \sqrt{\frac{z}{L}+\frac{M}{m}}\right)Y_0\left(\sqrt{\frac{M}{m}}\xi \right)-Y_0\left(\xi \sqrt{\frac{z}{L}+\frac{M}{m}}\right)J_0\left(\sqrt{\frac{M}{m}}\xi \right)\right\}\end{array}}$

Φ(z) se multiplica por un factor de modo que

${\displaystyle {\displaystyle \underset{0}{\overset{L}{\int }}{\Phi }_n^2(z)dz=1}}$

L=1; %longitud
q=0.25; %relación entre masas M/m
x=linspace(1,20,10);
f=@(x) besselj(0,sqrt(q)*x).*bessely(0,sqrt(1+q)*x)-
bessely(0,sqrt(q)*x).*besselj(0,sqrt(1+q)*x);
raiz=raices(f,x);

hold on
for xi=raiz
    fx=@(z) bessely(0,sqrt(q)*xi)*besselj(0,xi*sqrt(z/L+q))-
bessely(0,xi*sqrt(z/L+q))* besselj(0,sqrt(q)*xi);
    g=@(z) fx(z).*fx(z);
    area=integral(g,0,L);
    fx=@(z) fx(z)/sqrt(area);
    fplot(fx, [0,1],'displayName',num2str(xi));
end
hold off
grid on
view([90 -90])
legend('-DynamicLegend','location','northwest')
xlabel('z/L')
ylabel('X(z)')
title('Modos de vibración')

Cuando x se hace grande las funciones J₀(x) e Y₀(x) tienden hacia

${\displaystyle \begin{array}{l}{J}_0(x)\cong \sqrt{\frac{2}{\pi x}}\cos \left(x-\frac{\pi }{4}\right)\\ Y_0(x)\cong \sqrt{\frac{2}{\pi x}}\sin \left(x-\frac{\pi }{4}\right)\end{array}}$

Sustituyendo en la ecuación transcendente J₀(x) e Y₀(x) por sus expresiones asintóticas, se simplifica notablemente

${\displaystyle \begin{array}{l}\sin \left(\left(\sqrt{1+\frac{M}{m}}-\sqrt{\frac{M}{m}}\right)\xi \right)=0\\ {\xi }_n=\frac{n\pi }{\sqrt{1+\frac{M}{m}}-\sqrt{\frac{M}{m}}}\end{array}}$

>>raiz
    raiz =    5.0431   10.1450   15.2351   20.3219   25.4073
>> (1:5)*pi/(sqrt(1+q)-sqrt(q))
     ans =    5.0832   10.1664   15.2496   20.3328   25.4160

Se obtienen unos valores de ξ_n bastante similares

El extremo inferior está libre

En la página titulada Modos de vibración de una cuerda con cuentas, estudiamos las vibraciones de una cuerda horizontal con una o más partículas (cuentas). Si la partícula de masa M está situada en la posición z₀. La condición que deberá complir la función Φ(z) continua en z₀, es

${\displaystyle {\left(T\frac{d\Phi }{dz}\right)}_{z_0+}-{\left(T\frac{d\Phi }{dz}\right)}_{z_0-}+M{\omega }^2\Phi =0}$

En este caso, la posición de la partícula de masa M es z₀=0, la tensión por encima es el peso de la partícula Mg y por debajo, no hay cuerda

${\displaystyle Mg{\left(\frac{d\Phi }{dz}\right)}_{z=0}+M{\omega }^2\Phi =0}$

esta es la condición de contorno que sustituye a Φ(0)=0 (extremo fijo)

Teniendo en cuenta que las derivadas de las funciones de Bessel, $\frac{d{J}_0(x)}{dx}=-J_1(x)$ y $\frac{d{Y}_0(x)}{dx}=-Y_1(x)$, la función Φ(z) y su derivada en z=0, valen

${\displaystyle \begin{array}{l}\frac{d\Phi }{dz}=-\frac{1}{2L}\frac{\xi }{\sqrt{\frac{z}{L}+\frac{M}{m}}}\left\{A{J}_1\left(\xi \sqrt{\frac{z}{L}+\frac{M}{m}}\right)+B{Y}_1\left(\xi \sqrt{\frac{z}{L}+\frac{M}{m}}\right)\right\}\\ {\frac{d\Phi }{dz}|}_{z=0}=-\frac{1}{2L}\frac{\xi }{\sqrt{\frac{M}{m}}}\left\{A{J}_1\left(\xi \sqrt{\frac{M}{m}}\right)+B{Y}_1\left(\xi \sqrt{\frac{M}{m}}\right)\right\}\\ \Phi (0)=A{J}_0\left(\sqrt{\frac{M}{m}}\xi \right)+B{Y}_0\left(\sqrt{\frac{M}{m}}\xi \right)\end{array}}$

La condición de contorno en z=0, se expresa

${\displaystyle -A{J}_1\left(\sqrt{\frac{M}{m}}\xi \right)-B{Y}_1\left(\sqrt{\frac{M}{m}}\xi \right)+\frac{\xi }{2}\sqrt{\frac{M}{m}}\left\{A{J}_0\left(\sqrt{\frac{M}{m}}\xi \right)+B{Y}_0\left(\sqrt{\frac{M}{m}}\xi \right)\right\}=0}$

que junto a la condicion de contorno en x=L, Φ(L)=0

${\displaystyle A{J}_0\left(\sqrt{1+\frac{M}{m}}\xi \right)+B{Y}_0\left(\sqrt{1+\frac{M}{m}}\xi \right)=0}$

constituyen un sistema homogéneo de dos ecuaciones, de las que se obtienen las raíces ξ_n y las frecuencias angulares ω_n de los modos de vibración

${\displaystyle \begin{array}{l}{Y}_0\left(\sqrt{1+\frac{M}{m}}\xi \right)\left\{\frac{\xi }{2}\sqrt{\frac{M}{m}}{J}_0\left(\sqrt{\frac{M}{m}}\xi \right)-J_1\left(\sqrt{\frac{M}{m}}\xi \right)\right\}-\\ J_0\left(\sqrt{1+\frac{M}{m}}\xi \right)\left\{\frac{\xi }{2}\sqrt{\frac{M}{m}}{Y}_0\left(\sqrt{\frac{M}{m}}\xi \right)-Y_1\left(\sqrt{\frac{M}{m}}\xi \right)\right\}=0\end{array}}$

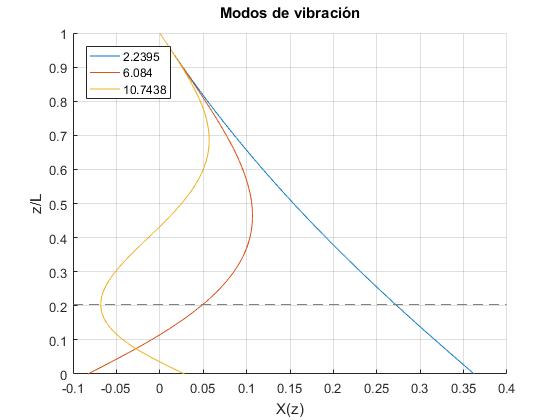
Calculamos las raíces de la ecuación transcendente, conocido el cociente M/m y representamos Φ(z)

${\displaystyle \begin{array}{l}\Phi (z)=A{J}_0\left(\xi \sqrt{\frac{z}{L}+\frac{M}{m}}\right)+B{Y}_0\left(\xi \sqrt{\frac{z}{L}+\frac{M}{m}}\right)=\\ A\left\{J_0\left(\xi \sqrt{\frac{z}{L}+\frac{M}{m}}\right)Y_0\left(\sqrt{1+\frac{M}{m}}\xi \right)-Y_0\left(\xi \sqrt{\frac{z}{L}+\frac{M}{m}}\right)J_0\left(\sqrt{1+\frac{M}{m}}\xi \right)\right\}\end{array}}$

L=1; %longitud
q=0.25; %relación entre masas M/m
x=linspace(1,15,15);
f=@(x) bessely(0,sqrt(1+q)*x).*(sqrt(q)*x.*besselj(0,sqrt(q)*x)/2-
besselj(1,sqrt(q)*x))-besselj(0,sqrt(1+q)*x).*(sqrt(q)*x.
*bessely(0,sqrt(q)*x)/2-bessely(1,sqrt(q)*x));
raiz=raices(f,x);

hold on
for xi=raiz
    fx=@(z) besselj(0,xi*sqrt(z/L+q))*bessely(0,sqrt(1+q)*xi)-
bessely(0,xi*sqrt(z/L+q))* besselj(0,sqrt(1+q)*xi);
    fplot(fx, [0,1],'displayName',num2str(xi));
end
hold off
grid on
view([90 -90])
legend('-DynamicLegend','location','northwest')
xlabel('z/L')
ylabel('X(z)')
title('Modos de vibración')

Referencias

Y Verbin. Boundary conditions and modes of the vertically hanging chain. Eur. J. Phys. 36 (2015) 015005