Varilla en posición horizontal

La ecuación diferencial del Movimiento Ondulatorio es

${\displaystyle \frac{{\partial }^2\psi }{\partial t^2}=c^2\frac{{\partial }^2\psi }{\partial x^2}}$

Donde c es la velocidad de propagación de las ondas longitudinales en la varilla.

${\displaystyle c=\sqrt{\frac{Y}{\rho }}}$

• Y es el módulo de la elasticidad del material o módulo de Young
• ρ es la densidad

Condiciones iniciales y de contorno

Para resolver la ecuación diferencial en derivadas parciales que es de segundo orden en x y en t, se precisa especificar dos condiciones iniciales: la deformación inicial de la varilla y la velocidad inicial de cada uno de sus puntos

${\displaystyle t=0\{\begin{array}{l}\psi (x\mathrm{,0})={\psi }_0(x)\\ {\frac{\partial \psi (x,t)}{\partial t}|}_{t=0}={\dot{\psi }}_0(x)\end{array}}$

y otras dos condiciones de contorno:

• Un extremo en x=0, es fijo

${\displaystyle \psi (\mathrm{0,}t)=0}$

• El otro extremo en x=l está libre

${\displaystyle {\frac{\partial \psi (x,t)}{\partial x}|}_{x=l}=0}$

Modos de vibración

Para resolver la ecuación diferencial dividimos la solución en producto de dos funciones una dependiente de x y la otra de t.

${\displaystyle \begin{array}{l}\psi (x,t)=\Phi (x)·T(t)\\ \frac{1}{T(t)}\frac{d^{2}T}{d{t}^2}=\frac{c^2}{\Phi (x)}\frac{d^2\Phi }{d{x}^2}=-{\omega }^2\end{array}}$

Como el miembro izquierdo depende solamente de t y el derecho solamente de x, entonces, igualamos ambos a una constante que denominaremos -ω²

${\displaystyle \begin{array}{l}\frac{d^{2}T}{d{t}^2}+{\omega }^2·T=0\\ \frac{d^2\Phi }{d{x}^2}+\frac{{\omega }^2}{c^2}\Phi =0\end{array}}$

Hemos sustituimos una ecuación diferencial en derivadas parciales por dos ecuaciones diferenciales. Ambas ecuaciones tienen soluciones conocidas, ecuación de las oscilaciones libres

${\displaystyle \begin{array}{l}T(t)=A\cos (\omega t)+B\sin (\omega t)\\ \Phi (x)=C\cos \left(\frac{\omega }{c}x\right)+D\sin \left(\frac{\omega }{c}x\right)\end{array}}$

Donde A, B, C y D se determinan a partir de las dos condiciones iniciales y las otras dos de contorno.

Si la varilla está sujeta por el extremo izquierdo x=0, entonces Φ(0)=0 y C=0.

Como el extremo x=l es libre

${\displaystyle \begin{array}{l}{\frac{d\Phi }{dx}|}_{x=l}=D\frac{\omega }{c}\cos \left(\frac{\omega }{c}l\right)=0\\ \frac{{\omega }_n}{c}l=\frac{2n+1}{2}\pi ,n=\mathrm{0,1,2,3...}\end{array}}$

ω_n son las frecuencias de los modos normales de vibración de la varilla

${\displaystyle {\Phi }_n(x)=\sin \left(\frac{{\omega }_n}{c}x\right)=\sin \left(\frac{2n+1}{2}\pi \frac{x}{l}\right)}$

La solución de la ecuación diferencial correspondiente al modo n de vibración es

${\displaystyle \begin{array}{l}{\psi }_n(x,t)={\Phi }_n(x)T_n(t)=\\ \sin \left(\frac{2n+1}{2}\pi \frac{x}{l}\right)\left\{A_n\cos \left(\frac{2n+1}{2}\pi \frac{ct}{l}\right)+B_n\sin \left(\frac{2n+1}{2}\pi \frac{ct}{l}\right)\right\}\end{array}}$

donde los coeficientes A_n y B_n se determinarán a partir de las condiciones iniciales

Superposición

La solución general que satisface las condiciones de contorno, es la superposición

${\displaystyle \begin{array}{l}\psi (x,t)={\displaystyle \sum _{n=0}^{\infty }{\psi }_n(x,t)}={\displaystyle \sum _{n=0}^{\infty }{\Phi }_n(x)\left(A_n\cos ({\omega }_{n}t)+B_n\sin ({\omega }_{n}t)\right)}\hfill \\ \psi (x,t)={\displaystyle \sum _{n=0}^{\infty }\sin \left(\frac{2n+1}{2}\pi \frac{x}{l}\right)\left\{A_n\cos \left(\frac{2n+1}{2}\pi \frac{ct}{l}\right)+B_n\sin \left(\frac{2n+1}{2}\pi \frac{ct}{l}\right)\right\}}\hfill \end{array}}$

Esta ecuación describe todos los posibles modos de vibración de la varilla. La vibración particular que experimenta está únicamente determinada por las condiciones iniciales, que a su vez determinan los valores de las constantes A_n y B_n.

${\displaystyle \begin{array}{l}\psi (x\mathrm{,0})={\psi }_0(x)\to {\displaystyle \sum _{n=0}^{\infty }{A}_n\sin \left(\frac{2n+1}{2}\pi \frac{x}{l}\right)}={\psi }_0(x)\hfill \\ {\frac{\partial \psi (x,t)}{\partial t}|}_{t=0}={\dot{\psi }}_0(x)\to {\displaystyle \sum _{n=0}^{\infty }\frac{2n+1}{2}\pi \frac{c}{l}{B}_n\sin \left(\frac{2n+1}{2}\pi \frac{x}{l}\right)}={\dot{\psi }}_0(x)\hfill \end{array}}$

Teniendo en cuenta el resultado de las integrales

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{l}{\int }}{\sin }^2\left(\frac{2n+1}{2}\pi \frac{x}{l}\right)dx}=\frac{l}{2}\\ {\displaystyle \underset{0}{\overset{l}{\int }}\sin \left(\frac{2n+1}{2}\pi \frac{x}{l}\right)\sin \left(\frac{2m+1}{2}\pi \frac{x}{l}\right)dx}=0m\ne n\end{array}}$

>> syms n x L;
>> assume(n,'integer');
>> int(sin((2*n+1)*pi*x/(2*L))^2,x,0,L)
ans =L/2 - (L*sin(pi*(2*n + 1)))/(2*pi*(2*n + 1))
>> simplify(ans)
ans =L/2

Los valores de A_n y B_n se determinan de modo análogo a los coeficientes de un desarrollo en serie de Fourier.

${\displaystyle \begin{array}{l}{A}_n=\frac{2}{l}{\displaystyle \underset{0}{\overset{l}{\int }}{\psi }_0(x)\sin \left(\frac{2n+1}{2}\pi \frac{x}{l}\right)dx}\\ B_n=\frac{4}{(2n+1)\pi c}{\displaystyle \underset{0}{\overset{l}{\int }}{\dot{\psi }}_0(x)\sin \left(\frac{2n+1}{2}\pi \frac{x}{l}\right)dx}\end{array}}$

Perturbación inicial

Supongamos que aplicamos una fuerza al extremo de la varilla, que la estira y luego, la soltamos

${\displaystyle \begin{array}{l}\psi (x\mathrm{,0})=kx,0\le x\le l\hfill \\ {\frac{\partial \psi (x,t)}{\partial x}|}_{t=0}=0\hfill \end{array}}$

Calculamos los coeficientes A_n integrando por partes. Los coeficientes B_n=0, son nulos.

${\displaystyle \begin{array}{l}{A}_n=\frac{2}{l}{\displaystyle \underset{0}{\overset{l}{\int }}kx\sin \left(\frac{2n+1}{2}\pi \frac{x}{l}\right)dx}\\ A_n=\frac{8kl{(-1)}^n}{{\left(2n+1\right)}^2{\pi }^2}\end{array}}$

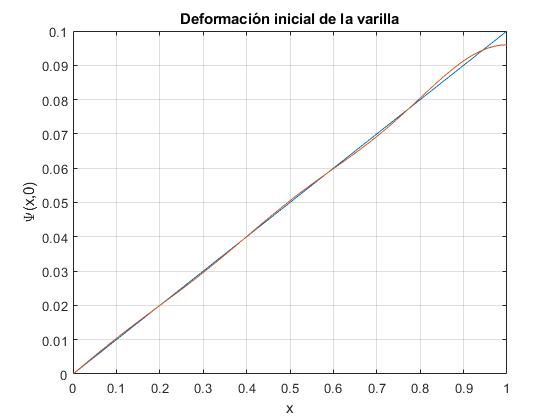
Aproximamos la deformación inicial de la cuerda Ψ(x,0) con los primeros cinco términos del desarrollo en serie

L=1; %longitud de la varilla
k=0.1; %constante
x=linspace(0,L,200);
y=k*x;
yy=zeros(1,length(x));
for n=0:4 %aproxima con cinco términos
    yy=yy+sin((2*n+1)*pi*x/(2*L))*(-1)^n/(2*n+1)^2;
end
yy=yy*(8*k*L/pi^2);
plot(x,y,x,yy)
xlabel('x')
ylabel('\Psi(x,0)')
title('Deformación inicial de la varilla')
grid on

Solución

La solución de la ecuación diferencial en derivadas parciales con las condiciones iniciales y de contorno especificadas es

${\displaystyle \psi (x,t)=\frac{8kl}{{\pi }^2}{\displaystyle \sum _{n=0}^{\infty }\frac{{(-1)}^n}{{\left(2n+1\right)}^2}\sin \left(\frac{2n+1}{2}\pi \frac{x}{l}\right)\cos \left(\frac{2n+1}{2}\pi \frac{ct}{l}\right)}}$

El desplazamiento del extremo x=l de la varilla es

${\displaystyle \begin{array}{l}\psi (l,t)=\frac{8kl}{{\pi }^2}{\displaystyle \sum _{n=0}^{\infty }\frac{{(-1)}^n}{{\left(2n+1\right)}^2}\sin \left(\frac{2n+1}{2}\pi \right)\cos \left(\frac{2n+1}{2}\pi \frac{ct}{l}\right)}=\\ \frac{8kl}{{\pi }^2}{\displaystyle \sum _{n=0}^{\infty }\frac{1}{{\left(2n+1\right)}^2}\cos \left(\frac{2n+1}{2}\pi \frac{ct}{l}\right)}\end{array}}$

Representamos el desplazamiento ψ(x,t) en función del tiempo, de los puntos situados en x=l/4, x=l/2, y x=l (extremo de la varilla), en este último caso, utilizamos la expresión simplificada ψ(l,t)

• Longitud de la varilla, l=1
• Velocidad de propagación, c=1
• Constante, k=0.1

L=1; %longitud de la varilla
c=1; %velocidad de propagación
k=0.1; %constante
t=linspace(0,4*L/c,200);
y=zeros(1,length(t));
hold on
x=L/4; %posición
for n=0:20 %aproxima con 20 términos
    y=y+(-1)^n*cos((2*n+1)*pi*c*t/(2*L))*sin((2*n+1)*pi*x/(2*L))/(2*n+1)^2;
end
y=y*(8*k*L/pi^2);
plot(t,y,'b')
x=L/2; %posición
y=zeros(1,length(t));
for n=0:20 
    y=y+(-1)^n*cos((2*n+1)*pi*c*t/(2*L))*sin((2*n+1)*pi*x/(2*L))/(2*n+1)^2;
end
y=y*(8*k*L/pi^2);
plot(t,y,'r')
%para x=L; posición
y=zeros(1,length(t));
for n=0:20 
    y=y+cos((2*n+1)*pi*c*t/(2*L))/(2*n+1)^2;
end
y=y*(8*k*L/pi^2);
plot(t,y,'k')
hold off
legend('L/4','L/2','L','Location','north')
xlabel('t')
ylabel('\Psi(x,t)')
title('Deformación de la varilla')
grid on

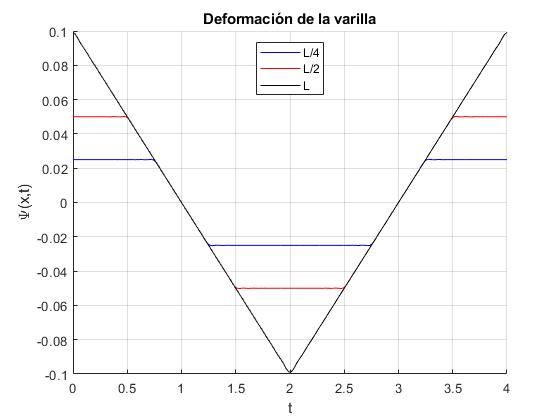
Los puntos interiores permanecen en reposo un tiempo

El periodo de la oscilación del extremo de la varilla es 4l/c

Actividades

Se introduce

• La constante k en el control titulado Constante
• La velocidad de propagación se ha fijado en c=1
• La longitud de la varilla se ha fijado en l=1

Se pulsa el botón titulado Nuevo

En la parte inferior, aparece la varilla en posición horizontal sujeta por su extremo izquierdo, el extremo derecho se ha desplazado kl y un punto de la varilla situado en x se ha desplazado kx. Observamos el desplazamiento los puntos situados en x=l/2 en color azul

Cuando se pulsa el botón titulado ►, la varilla deformada se suelta en el instante t=0

Observamos la vibración de los puntos de la varilla. En la parte superior, se representa a otra escala ψ(x,t)

En la parte superior derecha, se proporcionan los datos del tiempo t y de la posición l+ψ(l,t) del extremo derecho de la varilla

Varilla en posición vertical

Consideremos el caso de una varilla de longitud l sin deformar que se mantiene en posición vertical sujeta por su extremo superior. En el instante t=0, se suelta el extremo inferior, la varilla se deforma.

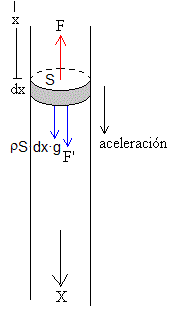
Deducimos la ecuación de propagación de las ondas longitudinales en la varilla cuando está en posición vertical

La parte superior de la varilla ejerce una fuerza F sobre el elemento de varilla de anchura dx, la parte inferior de la barra ejerce una fuerza F' sobre dicho elemento. La diferencia dF=F'-F es

${\displaystyle F\text{'}-F=dF=SY\frac{{\partial }^2\psi }{\partial x^2}dx}$

A la que hay que sumar el peso de dicho elemento, (ρS·dx)g. La segunda ley de Newton afirma que la fuerza sobre dicho elemento es igual al producto de la masa (densidad por volumen) por la aceleración (derivada segunda del desplazamiento)

${\displaystyle (\rho Sdx)g+dF=(\rho Sdx)\frac{{\partial }^2\psi }{\partial t^2}}$

La ecuación diferencial de un movimiento ondulatorio cuando la varilla está en posición vertical es

${\displaystyle \frac{{\partial }^2\psi }{\partial t^2}=c^2\frac{{\partial }^2\psi }{\partial x^2}+g,c=\sqrt{\frac{Y}{\rho }}}$

Condiciones iniciales y de contorno

Resolvemos esta ecuación diferencial con las condiciones de contorno: El extremo superior x=0, está fijo. El extremo inferior x=l está libre para t≥0

${\displaystyle \begin{array}{l}\psi (\mathrm{0,}t)=0\\ {\frac{\partial \psi (x,t)}{\partial x}|}_{x=l}=0\end{array}}$

Las conciones iniciales son

En el instante t=0, la varilla está en posición vertical sin deformar

${\displaystyle \begin{array}{l}\psi (x\mathrm{,0})=0\\ {\frac{\partial \psi (x,t)}{\partial t}|}_{t=0}=0\end{array}}$

En la sección anterior, hemos obtenido la solución de la ecuación diferencial homogénea bajo las mismas condiciones de contorno, tiene la forma

${\displaystyle \psi (x,t)={\displaystyle \sum _{n=0}^{\infty }{u}_n(t)\sin \left(\frac{2n+1}{2}\pi \frac{x}{l}\right)}}$

Donde u_n(t) era una función proporcional a cos(ω_nt). Para este caso, vamos a determinar la forma de u_n(t) sustituyendo la solución en la ecuación diferencial del movimiento ondulatorio cuando la varilla está en posición vertical.

${\displaystyle \begin{array}{l}\frac{{\partial }^2\psi }{\partial t^2}=c^2\frac{{\partial }^2\psi }{\partial x^2}+g\\ {\displaystyle \sum _{n=0}^{\infty }\left(\frac{d^2{u}_n}{d{t}^2}+c^2{\left(\frac{2n+1}{2l}\pi \right)}^2{u}_n\right)\sin \left(\frac{2n+1}{2}\pi \frac{x}{l}\right)=g}\end{array}}$

Multiplicamos por sin((2m+1)πx/(2l)) e integramos entre 0 y l. Teniendo en cuenta el resultado de las integrales

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{l}{\int }}{\sin }^2\left(\frac{2n+1}{2}\pi \frac{x}{l}\right)dx}=\frac{l}{2}\\ {\displaystyle \underset{0}{\overset{l}{\int }}\sin \left(\frac{2n+1}{2}\pi \frac{x}{l}\right)\sin \left(\frac{2m+1}{2}\pi \frac{x}{l}\right)dx}=0m\ne n\end{array}}$

Transformamos una ecuación diferencial en derivadas parciales en infinitas ecuaciones diferenciales de segundo orden, fáciles de resolver

${\displaystyle \begin{array}{l}{\displaystyle \sum _{n=0}^{\infty }\left(\frac{d^2{u}_n}{d{t}^2}+c^2{\left(\frac{2n+1}{2l}\pi \right)}^2{u}_n\right){\displaystyle \underset{0}{\overset{l}{\int }}\sin \left(\frac{2n+1}{2}\pi \frac{x}{l}\right)\sin \left(\frac{2m+1}{2}\pi \frac{x}{l}\right)dx}=g{\displaystyle \underset{0}{\overset{l}{\int }}\sin \left(\frac{2m+1}{2}\pi \frac{x}{l}\right)dx}}\\ \frac{l}{2}\left\{\frac{d^2{u}_n}{d{t}^2}+c^2{\left(\frac{2n+1}{2l}\pi \right)}^2{u}_n\right\}=g\frac{2l}{\left(2n+1\right)\pi }\\ \frac{d^2{u}_n}{d{t}^2}+c^2{\left(\frac{2n+1}{2l}\pi \right)}^2{u}_n=g\frac{4}{\left(2n+1\right)\pi }\end{array}}$

La solución de la homogénea es A_ncos(ω_nt)+B_nsin(ω_nt)

La solución particular de la ecuación diferencial es

${\displaystyle C=\frac{g\frac{4}{\left(2n+1\right)\pi }}{c^2{\left(\frac{2n+1}{2l}\pi \right)}^2}=\frac{16g{l}^2}{c^2{\left(2n+1\right)}^3{\pi }^3}}$

La forma funcional de u_n(t) es

${\displaystyle u_n(t)=A_n\cos \left(\frac{2n+1}{2}\pi \frac{ct}{l}\right)+B_n\sin \left(\frac{2n+1}{2}\pi \frac{ct}{l}\right)+\frac{16g{l}^2}{c^2{\left(2n+1\right)}^3{\pi }^3}}$

El desplazamiento de cualquier punto x de la barra en el instante t es

${\displaystyle \psi (x,t)={\displaystyle \sum _{n=0}^{\infty }\left\{A_n\cos \left(\frac{2n+1}{2}\pi \frac{ct}{l}\right)+B_n\sin \left(\frac{2n+1}{2}\pi \frac{ct}{l}\right)+\frac{16g{l}^2}{c^2{\left(2n+1\right)}^3{\pi }^3}\right\}\sin \left(\frac{2n+1}{2}\pi \frac{x}{l}\right)}}$

Donde A_n y B_n se calculan a partir de las condiciones iniciales

${\displaystyle \begin{array}{l}{A}_n=-\frac{16g{l}^2}{c^2{\left(2n+1\right)}^3{\pi }^3},B_n=0\\ \psi (x,t)=\frac{16g{l}^2}{c^2{\pi }^3}{\displaystyle \sum _{n=0}^{\infty }\frac{1}{{\left(2n+1\right)}^3}\left(1-\cos \left(\frac{2n+1}{2}\pi \frac{ct}{l}\right)\right)\sin \left(\frac{2n+1}{2}\pi \frac{x}{l}\right)}\\ \psi (x,t)=\frac{32g{l}^2}{c^2{\pi }^3}{\displaystyle \sum _{n=0}^{\infty }\frac{1}{{\left(2n+1\right)}^3}{\sin }^2\left(\frac{2n+1}{4}\pi \frac{ct}{l}\right)\sin \left(\frac{2n+1}{2}\pi \frac{x}{l}\right)}\end{array}}$

Calculamos el desplazamiento del extremo de la varilla x=l en cada instante

${\displaystyle \psi (l,t)=\frac{32g{l}^2}{c^2{\pi }^3}{\displaystyle \sum _{n=0}^{\infty }\frac{{(-1)}^n}{{\left(2n+1\right)}^3}{\sin }^2\left(\frac{2n+1}{4}\pi \frac{ct}{l}\right)}}$

Su valor máximo se alcanza cuando ct/(2l)=1,3,5.... El periodo de la oscilación, por ejemplo, del extremo inferior es 4l/c

${\displaystyle {\psi }_{máx}=\frac{32g{l}^2}{c^2{\pi }^3}{\displaystyle \sum _{n=0}^{\infty }\frac{{(-1)}^n}{{\left(2n+1\right)}^3}}=\frac{32g{l}^2}{c^2{\pi }^3}\frac{{\pi }^3}{32}=\frac{g{l}^2}{c^2}}$

Comprobamos que la suma de la serie vale π³/32

>> syms n;
>> symsum((-1)^n/(2*n+1)^3,n,0,inf)
ans =pi^3/32   

La longitud de la varilla varía entre l y l+gl²/c²

Representamos el desplazamiento ψ(x,t) en función del tiempo, de los puntos situados en x=l/4, x=l/2, y x=l (extremo de la varilla), en este último caso, utilizamos la expresión simplificada ψ(l,t)

• Longitud de la varilla, l=1
• Velocidad de propagación, c=2

L=1; %longitud de la varilla
c=2; %velcidad de propagación
t=linspace(0,4*L/c,200);
hold on
y=zeros(1,length(t));
x=L/4; %posición
for n=0:20 %aproxima con20 términos
    y=y+sin((2*n+1)*pi*x/(2*L))*sin((2*n+1)*pi*c*t/(4*L)).^2/(2*n+1)^3;
end
y=y*(32*9.8*L^2/(c^2*pi^3));
plot(t,y,'b')
x=L/2; %posición
y=zeros(1,length(t));
for n=0:20 %aproxima con20 términos
    y=y+sin((2*n+1)*pi*x/(2*L))*sin((2*n+1)*pi*c*t/(4*L)).^2/(2*n+1)^3;
end
y=y*(32*9.8*L^2/(c^2*pi^3));
plot(t,y,'r')
x=L; %posición
y=zeros(1,length(x));
for n=0:20 %aproxima con 20 términos
    y=y+(-1)^n*sin((2*n+1)*pi*c*t/(4*L)).^2/(2*n+1)^3;
end
y=y*(32*9.8*L^2/(c^2*pi^3));
plot(t,y,'k')
hold off
legend('L/4','L/2','L')
xlabel('t')
ylabel('\Psi(x,t)')
title('Deformación de la varilla')
grid on

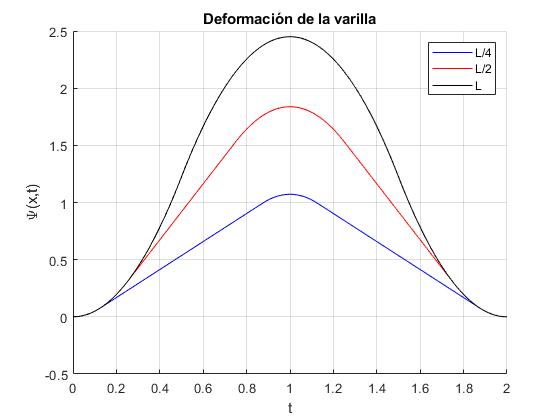
El periodo de la oscilación del extremo de la varilla es 4l/c=2, y la máxima deformación del extremo x=l de la varilla es gl²/c²=2.45

Actividades

Se introduce

• La velocidad de propagación c del movimiento ondulatorio longitudinal en la varilla
• La longitud de la varilla se ha fijado en l=1

Se pulsa el botón titulado Nuevo

Aparece la varilla en posición vertical sujeta por su extremo superior, se sostiene el extremo inferior en la posición x=l, varilla sin deformar

Cuando se pulsa el botón titulado ►, el extremo inferior de la varilla se suelta en el instante t=0

Observamos la vibración de los puntos de la varilla y en particular, los puntos situados en x=l/2 en color azul

En la parte superior derecha, se proporcionan los datos del tiempo t y de la posición l+ψ(l,t) del extremo inferior de la varilla

El periodo de oscilación es

Referencias

N. S. Kosholyakov, M. M. Smirnov, E. B. Gliner. Differential equations of Mathematical Physics. North-Holland Publishing Company (1964) pp. 123-126, 139-141