En esta página resolveremos la ecuación diferencial

${\displaystyle \frac{{\partial }^2\psi }{\partial t^2}+2\gamma \frac{\partial \psi }{\partial t}-c^2\frac{{\partial }^2\psi }{\partial x^2}=\frac{1}{\mu }f(x,t)}$

Con las condiciones iniciales

${\displaystyle t=0\{\begin{array}{l}\psi (x\mathrm{,0})={\psi }_0(x)\\ {\frac{\partial \psi (x,t)}{\partial t}|}_{t=0}={\dot{\psi }}_0(x)\end{array}}$

y de contorno:

• Un extremo en x=0, es fijo

${\displaystyle \psi (\mathrm{0,}t)=0}$

• El otro extremo en x=l está fijo

${\displaystyle \psi (l,t)=0}$

Como hemos visto para los modos de oscilación libre y amortiguado, la forma de la solución es

${\displaystyle \psi (x,t)={\displaystyle \sum _{n=1}^{\infty }{u}_n(t)\sin \left(n\pi \frac{x}{l}\right)}}$

Sustituimos en la ecuación diferencial

${\displaystyle {\displaystyle \sum _{n=1}^{\infty }\left\{\frac{d^2{u}_n}{d{t}^2}+2\gamma \frac{d{u}_n}{dt}+c^2{\left(\frac{n\pi }{l}\right)}^2{u}_n\right\}\sin \left(\frac{n\pi }{l}x\right)}=\frac{1}{\mu }f(x,t)}$

Multiplicamos por sin(mπx/l) e integramos entre 0 y l. Teniendo en cuenta el resultado de las integrales

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{l}{\int }}{\sin }^2\left(n\pi \frac{x}{l}\right)dx}=\frac{l}{2}\hfill \\ {\displaystyle \underset{0}{\overset{l}{\int }}\sin \left(n\pi \frac{x}{l}\right)\sin \left(m\pi \frac{x}{l}\right)dx}=0m\ne n\hfill \end{array}}$

Transformamos una ecuación diferencial en derivadas parciales en infinitas ecuaciones diferenciales de segundo orden

${\displaystyle \begin{array}{l}\frac{d^2{u}_n}{d{t}^2}+2\gamma \frac{d{u}_n}{dt}+c^2{\left(\frac{n\pi }{l}\right)}^2{u}_n=\frac{2}{\mu l}{\displaystyle \underset{0}{\overset{l}{\int }}f(x,t)\sin \left(\frac{n\pi }{l}x\right)dx}\\ \frac{d^2{u}_n}{d{t}^2}+2\gamma \frac{d{u}_n}{dt}+{\omega }_{0n}^2{u}_n=q_n(t)\end{array}}$

Aplicando la transformada de Laplace a la ecuación diferencial, con las condiciones iniciales

${\displaystyle \{\begin{array}{l}{u}_n(0)=u_{0n}\\ {\frac{d{u}_n}{dt}|}_{t=0}=v_{0n}\end{array}}$

Se obtiene

${\displaystyle \begin{array}{l}\left(s^{2}F(s)-s·u_n(0)-{\frac{d{u}_n}{dt}|}_{t=0}\right)+2\gamma \left(sF(s)-u_n(0)\right)+{\omega }_{0n}^{2}F(s)=g_n(s)\hfill \\ \left(s^{2}F(s)-s·u_{0n}-v_{0n}\right)+2\gamma \left(sF(s)-u_{0n}\right)+{\omega }_{0n}^{2}F(s)=g_n(s)\hfill \\ F(s)=\frac{g_n(s)}{s^2+2\gamma s+{\omega }_{0n}^2}+\frac{s{u}_{0n}+2\gamma u_{0n}+v_{0n}}{s^2+2\gamma s+{\omega }_{0n}^2}\hfill \end{array}}$

El primer término depende de la transformada g(s) de la fuerza externa y el segundo de las condiciones iniciales

El caso más simple se produce cuando la cuerda está inicialmente t=0, sin deformar y en reposo

${\displaystyle \{\begin{array}{l}\psi (x\mathrm{,0})={\displaystyle \sum _{n=1}^{\infty }{u}_n(0)\sin \left(n\pi \frac{x}{l}\right)=0}\\ {\frac{\partial \psi (x,t)}{\partial t}|}_{t=0}={\displaystyle \sum _{n=1}^{\infty }{\frac{d{u}_n}{dt}|}_{t=0}\sin \left(n\pi \frac{x}{l}\right)=0}\end{array}}$

La primera ecuación da u_n(0)=u_0n=0, la segunda, v_0n=0

La transformada de Laplace, se reduce a

${\displaystyle F(s)=\frac{g_n(s)}{s^2+2\gamma s+{\omega }_{0n}^2}}$

Se aplica a todos los puntos de la cuerda una fuerza que cambia con el tiempo

Aplicamos a todos los puntos x de la cuerda, la fuerza f(x,t)=Aμsin(ωt)

${\displaystyle \begin{array}{l}{q}_n(t)=\frac{2}{\mu l}{\displaystyle \underset{0}{\overset{l}{\int }}f(x,t)\sin \left(\frac{n\pi }{l}x\right)dx}=\frac{2}{l}A\sin \left(\omega t\right){\displaystyle \underset{0}{\overset{l}{\int }}\sin \left(\frac{n\pi }{l}x\right)dx}=\frac{4}{n\pi }\sin \left(\omega t\right)\\ n=\mathrm{1,3,5,...}\end{array}}$

Para hacer más simple este primer ejemplo, supondremos que no hay rozamiento, γ=0.

Consultamos en las tablas la transformada de Laplace de sin(ωt). Escribimos F(s) de modo que se pueda aplicar transformada inversa de Laplace mirando directamente a la tabla de transformadas.

${\displaystyle F(s)=\frac{4A}{n\pi }\frac{\frac{\omega }{s^2+{\omega }^2}}{s^2+{\omega }_{0n}^2}=\frac{4A}{n\pi }\frac{1}{{\omega }_{0n}^2-{\omega }^2}\left\{\frac{\omega }{s^2+{\omega }^2}-\frac{\omega }{{\omega }_{0n}}\frac{{\omega }_n}{s^2+{\omega }_{0n}^2}\right\}}$

El resultado es

${\displaystyle u_n(t)=\frac{4A}{n\pi }\frac{1}{{\omega }_{0n}^2-{\omega }^2}\left\{\sin \left(\omega t\right)-\frac{\omega }{{\omega }_{0n}}\sin \left({\omega }_{0n}t\right)\right\},n=\mathrm{1,3,5...}}$

La solución completa es

${\displaystyle \begin{array}{l}\psi (x,t)=\frac{4A}{\pi }{\displaystyle \sum _{n=\mathrm{1,3,5..}}^{\infty }\frac{1}{n\left({\omega }_{0n}^2-{\omega }^2\right)}\left\{\sin \left(\omega t\right)-\frac{\omega }{{\omega }_{0n}}\sin \left({\omega }_{0n}t\right)\right\}\sin \left(n\pi \frac{x}{l}\right)}\\ {\omega }_{0n}=n\pi \frac{c}{l}\end{array}}$

Cuando la frecuencia de la fuerza oscilante ω es próxima a la frecuencia de un modo normal de vibración ω_0n, Ψ(x,t) se expresa

>> syms w w0 t;
>> y=(sin(w*t)-w*sin(w0*t)/w0)/(w0^2-w^2);
>> limit(y,w,w0)
ans =(sin(t*w0) - t*w0*cos(t*w0))/(2*w0^2)

${\displaystyle \psi (x,t)=\frac{2A}{\pi }{\displaystyle \sum _{n=\mathrm{1,3,5..}}^{\infty }\frac{\sin \left({\omega }_{0n}t\right)-t·{\omega }_{0n}\cos \left({\omega }_{0n}t\right)}{n{\omega }_{0n}^2}\sin \left(n\pi \frac{x}{l}\right)}}$

Actividades

Se introduce

• la velocidad de propagación c, en el control titulado Velocidad.
• la frecuencia de la fuerza oscilante ω, en el control titulado Frecuencia (Hz)

Se pulsa en el botón titulado Nuevo.

Para cambiar la escala de la representación gráfica, se actúa en el control titulado Escala.

En la parte superior izquierda, se indica si la frecuencia de la fuerza oscilante ω corresponde a un modo de vibración

Se aplica a un punto de la cuerda una fuerza que cambia con el tiempo

En este apartado simulamos la experiencia de laboratorio, Modos de vibración de una cuerda sujeta por ambos extremos

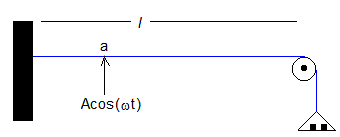
Supongamos que se aplica a un punto a de la cuerda la fuerza Acos(ωt). La fuerza f(x,t) se expresa

${\displaystyle f(x,t)=A\cos \left(\omega t\right)\delta \left(x-a\right)}$

Calculamos la integral

${\displaystyle q_n(t)=\frac{2}{\mu l}{\displaystyle \underset{0}{\overset{L}{\int }}A\cos \left(\omega t\right)\delta (x-a)\sin \left(\frac{n\pi }{l}x\right)dx}=\frac{2}{\mu l}A\cos \left(\omega t\right)\sin \left(\frac{n\pi }{l}a\right)}$

La transformada de Laplace g(s) es, véase la tabla de transformadas de Laplace

${\displaystyle \begin{array}{l}{g}_n(s)=\frac{2}{\mu l}A\sin \left(\frac{n\pi }{l}a\right)\frac{s}{s^2+{\omega }^2}=f_a\frac{s}{s^2+{\omega }^2}\\ F(s)=\frac{f_{a}s}{\left(s^2+2\gamma s+{\omega }_{0n}^2\right)\left(s^2+{\omega }^2\right)}\end{array}}$

Descomponemos en fracciones simples

${\displaystyle \begin{array}{l}F(s)=\frac{f_{a}s}{\left(s^2+2\gamma s+{\omega }_{0n}^2\right)\left(s^2+{\omega }^2\right)}=f_a\left\{\frac{As+B}{s^2+2\gamma s+{\omega }_{0n}^2}+\frac{Cs+D}{s^2+{\omega }^2}\right\}\\ C=\frac{{\omega }_{0n}^2-{\omega }^2}{{\left({\omega }_{0n}^2-{\omega }^2\right)}^2+4{\gamma }^2{\omega }^2},A=-\frac{{\omega }_{0n}^2-{\omega }^2}{{\left({\omega }_{0n}^2-{\omega }^2\right)}^2+4{\gamma }^2{\omega }^2}\\ D=\frac{2\gamma {\omega }^2}{{\left({\omega }_{0n}^2-{\omega }^2\right)}^2+4{\gamma }^2{\omega }^2},B=-\frac{2\gamma {\omega }_{0n}^2}{{\left({\omega }_{0n}^2-{\omega }^2\right)}^2+4{\gamma }^2{\omega }^2}\end{array}}$

Escribimos F(s) de modo que se pueda aplicar transformada inversa de Laplace mirando directamente a la tabla de transformadas.

${\displaystyle \begin{array}{l}F(s)=f_a\left\{A\frac{s+\gamma }{{\left(s+\gamma \right)}^2+\left({\omega }_{0n}^2-{\gamma }^2\right)}+\frac{B-A\gamma }{\sqrt{{\omega }_{0n}^2-{\gamma }^2}}\frac{\sqrt{{\omega }_{0n}^2-{\gamma }^2}}{{\left(s+\gamma \right)}^2+\left({\omega }_{0n}^2-{\gamma }^2\right)}+C\frac{s}{s^2+{\omega }^2}+\frac{D}{\omega }\frac{\omega }{s^2+{\omega }^2}\right\}\\ u_n(t)=f_a\left\{\exp (-\gamma t)\left(A\cos \left({\omega }_{n}t\right)+\frac{B-A\gamma }{{\omega }_n}\sin \left({\omega }_{n}t\right)\right)+C\cos \left(\omega t\right)+\frac{D}{\omega }\sin \left(\omega t\right)\right\}\\ u_n(t)=\frac{\frac{2}{\mu l}A\sin \left(\frac{n\pi }{l}a\right)}{{\left({\omega }_{0n}^2-{\omega }^2\right)}^2+4{\gamma }^2{\omega }^2}\left\{\begin{array}{l}-\left({\omega }_{0n}^2-{\omega }^2\right)\exp (-\gamma t)\left(\cos \left({\omega }_{n}t\right)+\frac{\gamma }{{\omega }_n}\sin \left({\omega }_{n}t\right)\right)\\ +\left({\omega }_{0n}^2-{\omega }^2\right)\cos \left(\omega t\right)+2\gamma \omega \sin \left(\omega t\right)\end{array}\right\}\end{array}}$

En el estado estacionario, cuando t→∞ la solución es

${\displaystyle u_n(t)=\frac{\frac{2}{\mu l}A\sin \left(\frac{n\pi }{l}a\right)}{{\left({\omega }_{0n}^2-{\omega }^2\right)}^2+4{\gamma }^2{\omega }^2}\left\{\left({\omega }_{0n}^2-{\omega }^2\right)\cos \left(\omega t\right)+2\gamma \omega \sin \left(\omega t\right)\right\}}$

La solución completa es

${\displaystyle \begin{array}{l}\psi (x,t)={\displaystyle \sum _{n=1}^{\infty }{u}_n(t)\sin \left(n\pi \frac{x}{l}\right)}=\\ \frac{2}{\mu l}A{\displaystyle \sum _{n=1}^{\infty }\frac{\sin \left(\frac{n\pi }{l}a\right)}{{\left({\omega }_{0n}^2-{\omega }^2\right)}^2+4{\gamma }^2{\omega }^2}\left\{\left({\omega }_{0n}^2-{\omega }^2\right)\cos \left(\omega t\right)+2\gamma \omega \sin \left(\omega t\right)\right\}\sin \left(n\pi \frac{x}{l}\right)}\\ {\omega }_{0n}=n\pi \frac{c}{l}\end{array}}$

Resonancia

Si la frecuencia angular ω de la fuerza oscilante producida por la membrana del altavoz coincide con la frecuencia ω_0n de algún modo de vibración de la cuerda se produce resonancia que incrementa la amplitud de las oscilaciones de los puntos de la cuerda, tal como vemos en la simulación en la página titulada Modos de vibración de una cuerda

Se introduce en el control titulado Frecuencia (Hz), 5 y en el control titulado Escala se selecciona un valor grande 50 ó 100, veremos que la cuerda vibra pero con una amplitud muy pequeña comparada a la misma escala con la del modo de vibración próximo, cuya frecuencia es 4

Las frecuencias angulares de los modos de vibración de la cuerda son, ω_0n=nπc/l, donde c es la velocidad de propagación de las ondas transversales y l es la longitud de la cuerda

Sea Acos(ωt) la fuerza oscilante aplicada a un punto a de la cuerda que no sea un nodo. hemos calculado el estado y de cada punto x de la cuerda en el instante t

Creamos una función que calcula la suma de los 50 primeros términos, de n=1 a 50. A esta función le pasamos los siguientes datos: posición a del punto de la cuerda donde se aplica la fuerza oscilante de frecuencia angular ω. La velocidad de propagación c de las ondas transversales. El punto x de la cuerda cuyo desplazamiento y queremos determinar. Establece un valor para el amortiguamiento γ.

function z = onda_estacionaria(x,c,a,w,t)
    gamma=0.2; %amortiguamiento
    z=0;
    for n=1:50
        z=z+2*sin(n*pi*a)*sin(n*pi*x)*((n^2*pi^2*c^2-w^2)*cos(w*t)+
2*gamma*w*sin(w*t))/((n^2*pi^2*c^2-w^2)^2+4*w^2*gamma^2);
    end
end

Creamos un script que establece los valores de la velocidad de propagación c, de la posición a del punto de la cuerda donde se aplica la fuerza oscilante de frecuencia angular ω que vamos a modificar. Se representa el estado de la cuerda y en los instantes: 0, P/8 y P/4, siendo P=2π/ω el periodo de vibración.

c=8; %velocidad de propagación
a=0.3; %posición de la fuente
w=4*2*pi; %frecuencia de la fuerza oscilante
%La longitud de la cuerda es L=1
%La amplitud de la fuerza oscilante A=1
 
hold on
for t=[0,pi/(4*w),pi/(2*w)];
    y=@(x) onda_estacionaria(x,c,a,w,t);
    fplot(y,[0,1])
end
hold off
legend('0','P/8','P/4');
grid on
xlabel('x')
ylabel('y')
title('Vibración de una cuerda')

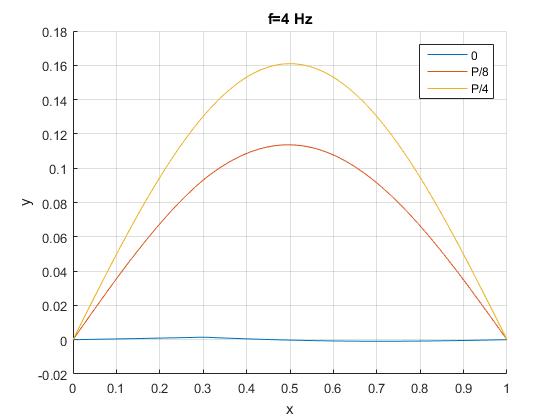
Si la velocidad de propagación c=8, los modos de vibración de la cuerda se producen para las frecuencias: 4, 8, 12...en una cuerda de longitud l=1.

Cuando la frecuencia de la fuerza oscilante ω coincide con un modo de vibración 4·2π, representamos el estado de la cuerda en tres instantes t=0, P/8, y P/4, donde P=2π/ω es el periodo

Cuando la frecuencia de la fuerza oscilante ω no coincide con un modo de vibración, 6·2π, representamos el estado de la cuerda en tres instantes t=0, P/8, y P/4

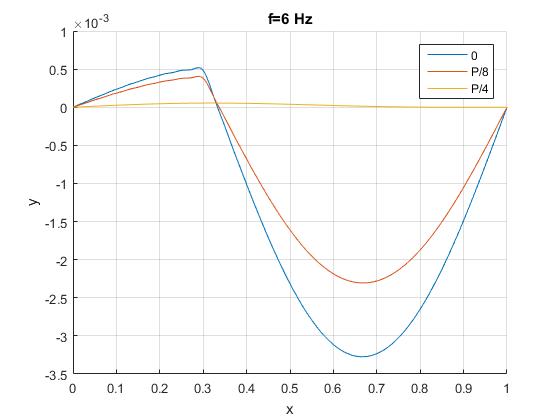
La vibración de la cuerda apenas se percibe, tal como comprobamos en el programa interctivo más abajo

Actividades

Se introduce

• la velocidad de propagación c, en el control titulado Velocidad.
• la frecuencia de la fuerza oscilante ω, en el control titulado Frecuencia (Hz)
• la constante de amortiguamiento γ>0 en el control titulado Amortiguamiento (mayor que cero, para evitar el cociente 0/0, cuando la frecuencia de la fuerza oscilante se hace igual a la de un modo de vibración ω=ω_0n)

Se pulsa en el botón titulado Nuevo.

Para cambiar la escala de la representación gráfica, se actúa en el control titulado Escala.

Como ejercicio, el lector puede hallar los primeros modos de vibración de una cuerda cuando sus velocidades de propagación son sucesivamente 4, 8, etc.

Los nodos, puntos cuya amplitud de oscilación es nula, se señalan mediante flechas de color rojo.

A bajas velocidades c, se observa la propagación del movimiento ondulatorio hacia los extremos y la reflexión en los puntos fijos x=0 y x=l

Fuerza aplicada en un punto y en un instante

En este apartado, las condiciones iniciales son distintas de cero, la transformada como hemos visto al principio de la página de Laplace consta de dos sumandos: el primero depende de la transformada g(s) de la fuerza externa y el segundo de las condiciones iniciales

Se trata de una fuerza grande que actúa en el instante τ durante un intervalo de tiempo muy pequeño en el punto x=a

${\displaystyle \begin{array}{l}f(x,t)=A\delta (x-a)\delta (t-\tau )\\ q_n(t)=\frac{2}{\mu l}{\displaystyle \underset{0}{\overset{l}{\int }}A\delta (x-a)\delta (t-\tau )\sin \left(\frac{n\pi }{l}x\right)dx}=\frac{2}{\mu l}A\sin \left(\frac{n\pi }{l}a\right)\delta (t-\tau )\end{array}}$

La transformada de Laplace g(s) es,

${\displaystyle g_n(s)=\frac{2}{\mu l}A\sin \left(\frac{n\pi }{l}a\right)\exp (-\tau s)=f_a\exp (-\tau s)}$

Escribimos F(s) de modo que se pueda aplicar transformada inversa de Laplace mirando directamente a la tabla de transformadas.

${\displaystyle \begin{array}{l}F(s)=\frac{f_a\exp (-\tau s)}{s^2+2\gamma s+{\omega }_{0n}^2}+\frac{s{u}_{0n}+2\gamma u_{0n}+v_{0n}}{s^2+2\gamma s+{\omega }_{0n}^2}\\ F(s)=\frac{f_a\exp (-\tau s)}{\sqrt{{\omega }_{0n}^2-{\gamma }^2}}\frac{\sqrt{{\omega }_{0n}^2-{\gamma }^2}}{{(s+\gamma )}^2+({\omega }_{0n}^2-{\gamma }^2)}+\frac{u_{0n}(s+\gamma )}{{(s+\gamma )}^2+({\omega }_{0n}^2-{\gamma }^2)}+\frac{(\gamma u_{0n}+v_{0n})}{\sqrt{{\omega }_{0n}^2-{\gamma }^2}}\frac{\sqrt{{\omega }_{0n}^2-{\gamma }^2}}{{(s+\gamma )}^2+({\omega }_{0n}^2-{\gamma }^2)}\\ u_n(t)=\frac{f_a}{{\omega }_n}\exp \left(-\gamma (t-\tau )\right)\sin \left({\omega }_n(t-\tau )\right)U(t-\tau )+\\ \exp \left(-\gamma t\right)\left\{u_{0n}\cos ({\omega }_{n}t)+\frac{(\gamma u_{0n}+v_{0n})}{{\omega }_n}\sin ({\omega }_{n}t)\right\}\end{array}}$

La función U(t-τ), es cero para t<τ y es uno para t≥τ

Condiciones iniciales

En la figura, se muestra la deformación inicial de una cuerda de longitud l

${\displaystyle \begin{array}{l}\psi (x\mathrm{,0})={\displaystyle \sum _{n=1}^{\infty }{u}_n(0)\sin \left(n\pi \frac{x}{l}\right)}=\{\begin{array}{l}2h\frac{x}{l}0\le x\le \frac{l}{2}\\ 2h\left(1-\frac{x}{l}\right)\frac{l}{2}<x\le l\end{array}\\ {\frac{\partial \psi (x,t)}{\partial x}|}_{t=0}={\displaystyle \sum _{n=1}^{\infty }{\frac{d{u}_n}{dt}|}_{t=0}\sin \left(n\pi \frac{x}{l}\right)=}0\\ {v_{0n}=\frac{d{u}_n}{dt}|}_{t=0}=0\end{array}}$

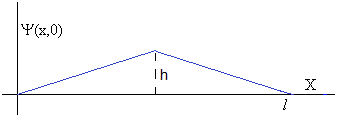
Calculamos los coeficientes u_0n, como en los modos de vibración amortiguados

${\displaystyle \begin{array}{l}{u}_n(0){\displaystyle \underset{0}{\overset{l}{\int }}{\sin }^2\left(n\pi \frac{x}{l}\right)}dx=\underset{0}{\overset{l/2}{{{\displaystyle \int }}^{\text{}}}}\left(2h\frac{x}{l}\right)\sin \left(n\pi \frac{x}{l}\right)dx+\underset{l}{\overset{l/2}{{{\displaystyle \int }}^{\text{}}}}2h\left(1-\frac{x}{l}\right)\sin \left(n\pi \frac{x}{l}\right)dx\\ u_{0n}=u_n(0)=\frac{8h}{n^2{\pi }^2}\sin \left(n\frac{\pi }{2}\right)\end{array}}$

La solución completa

${\displaystyle \psi (x,t)={\displaystyle \sum _{n=1}^{\infty }\left\{\begin{array}{l}\frac{\frac{2}{\mu l}A\sin {\left(\frac{n\pi }{l}a\right)}_a}{{\omega }_n}\exp \left(-\gamma (t-\tau )\right)\sin \left({\omega }_n(t-\tau )\right)U(t-\tau )+\\ \frac{8h}{n^2{\pi }^2}\sin \left(n\frac{\pi }{2}\right)\exp (-\gamma t)\left(\cos ({\omega }_{n}t)+\frac{\gamma }{{\omega }_n}\sin ({\omega }_{n}t)\right)\end{array}\right\}\sin \left(n\pi \frac{x}{l}\right)}}$

Actividades

Se introduce

• la velocidad de propagación c, en el control titulado Velocidad.
• la frecuencia de la fuerza oscilante ω, en el control titulado Frecuencia (Hz)
• la constante de amortiguamiento γ en el control titulado Amortiguamiento
• la posición a donde se aplica la fuerza, en el control titulado Posición
• El instante τ en se aplica la fuerza, en el control titulado Tiempo
• El módulo A de la fuerza, en el control titulado Amplitud

Se pulsa en el botón titulado Nuevo.

Primero se observan las oscilaciones amortiguadas de la cuerda, tal como se ha descrito en la página titulada Modos de vibración amortiguados en una cuerda. Después se observa el efecto de la fuerza aplicada en el instante τ. Una flecha de color rojo lo señala

Referencias

V. Migulin. V. Medvedev. E. Mustel. V. Parygin. Basic theory of oscillations. Mir Publishers Moscow. 1983. pp. 335-338.

Daniel S. Stutts. Modal Analysis of a Tight String http://web.mst.edu/~stutts/PRESENTATIONS/ModalAnalysisofaTightString.pdf