Esta página, es similar a la primera parte de la página titulada Modos de vibración de una cuerda con cuentas dedicada al cálculo de las frecuencias de los modos de vibración. Por lo que recomendamos que se lea antes.

El resonador en posición simétrica

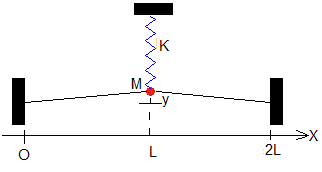
Sea una cuerda de longitud 2L y densidad lineal μ₀=m/L, sujeta por ambos extremos, cuya tensión es T en la que se colocado una masa puntual M unida a un muelle elástico de constante K en su punto medio (un resonador), tal como se muestra en la figura.

La fuerza sobre la partícula de masa M situada en la mitad de la cuerda x=L y unida a un muelle de constante elástica K que se ha deformado y es

${\displaystyle \left({\left(T\frac{\partial y}{\partial x}\right)}_{L+}-{\left(T\frac{\partial y}{\partial x}\right)}_{L-}\right)-Ky=M\frac{{\partial }^{2}y}{\partial t^2}}$

Hemos aplicado la segunda ley de Newton, fuerza =masa×aceleración

Escribimos la solución de la ecuación diferencial en derivadas parciales como producto, y(x,t)=Φ(x)·cos(ωt)

${\displaystyle \begin{array}{l}\frac{d}{dx}\left(\frac{d\Phi }{dx}T(x)\right)+\mu {\omega }^2\Phi =0\\ \left({\left(T\frac{d\Phi }{dx}\right)}_{L+}-{\left(T\frac{d\Phi }{dx}\right)}_{L-}\right)-K\Phi +M{\omega }^2\Phi =0\end{array}}$

Consideramos que la tensión T(x)=T de la cuerda es constante, su densidad μ₀=m/L es constante.

${\displaystyle \begin{array}{l}\frac{d^2\Phi }{d{x}^2}+k^2\Phi =0\\ \omega =k\sqrt{\frac{T}{{\mu }_0}}=kv\end{array}}$

El término, bajo la raíz cuadrada es la velocidad de propagación de las ondas transversales en una cuerda. La solución de esta ecuación diferencial tiene la forma conocida, Asin(kx)+Bcos(kx)

La masa puntual M situada en la posición x=L, divide a la cuerda en dos partes. Probamos la solución

${\displaystyle \Phi (x)=\{\begin{array}{l}A\sin (kx)+B\cos (kx)0\le x<L\\ C\sin \left(k(x-L)\right)+D\cos \left(k(x-L)\right)L\le x<2L\end{array}}$

Los extremos de la cuerda x=0 y x=2L son fijos. Φ(0)=0 y Φ(2L)=0, por lo que el coeficiente B=0 y se cumplirá que, Csin(kL)+Dcos(kL)=0

${\displaystyle \Phi (x)=\{\begin{array}{l}A\sin (kx)0\le x<L\\ C\sin \left(k(x-L)\right)+D\cos \left(k(x-L)\right)L\le x<2L\end{array}}$

En x=L se ha situado una masa puntual M, la función Φ(x) es continua en este punto

Asin(kL)=D

Modos de vibración de orden par

Combinando esta relación con la relación entre los coeficientes C y D,

${\displaystyle \sin (kL)\left(C+A\cos (kL)\right)=0}$

Una solución es

sin(kL)=0, k_nL=nπ, n=1,2,3...

Sabiendo que k=2π/λ, 2L=nλ_n, un número entero de longitudes de onda cabe en la cuerda de longitud 2L sujeta por ambos extremos, estos son los modos pares de vibración de la cuerda

La otra solución es, C=-Acos(kL)

Modos de vibración de orden impar

Por otra parte, la función Φ(x) ha de satisfacer la condición

${\displaystyle \begin{array}{l}\left({\left(\frac{d\Phi }{dx}\right)}_{L+}-{\left(\frac{d\Phi }{dx}\right)}_{L-}\right)-\frac{K}{T}\Phi (L)+\frac{M}{T}{\omega }^2\Phi (L)=0\\ Ck-Ak\cos \left(kL\right)-\frac{K}{T}A\sin \left(kL\right)+\frac{M}{T}{\omega }^{2}A\sin \left(kL\right)=0\\ -Ak\cos (kL)-Ak\cos \left(kL\right)-\frac{K}{T}A\sin \left(kL\right)+\frac{M}{T}{\omega }^{2}A\sin \left(kL\right)=0\\ \frac{M{k}^2{v}^2-K}{kT}\sin \left(kL\right)-2\cos \left(kL\right)=0\end{array}}$

Resolvemos esta ecuación transcendente para obtener las raíces k_nL

Casos particulares

• La masa de la partícula es nula, M=0, solamente tenemos el muelle elástico de constante K

${\displaystyle \begin{array}{l}\frac{K}{kT}\sin \left(kL\right)+2\cos \left(kL\right)=0\\ \tan \left(kL\right)=-\frac{2kT}{K}=-\frac{2T}{LK}\left(kL\right)\end{array}}$

Las raíces k_nL son los puntos de intersección de la recta y=-ax y de y=tan(x) con x=kL y a=4T/(LK).

fplot(@(x) tan(x), [0, 2*pi])
a=0.5;
line([0, 2*pi],[0,-2*a*2*pi], 'color','r')
ylim([-15,5])
set(gca,'XTick',0:pi/2:2*pi)
set(gca,'XTickLabel',{'0','\pi/2','\pi','3\pi/2','2\pi'})
grid on
xlabel('kL/2')
ylabel('y')
title('Raíces de la ecuación')



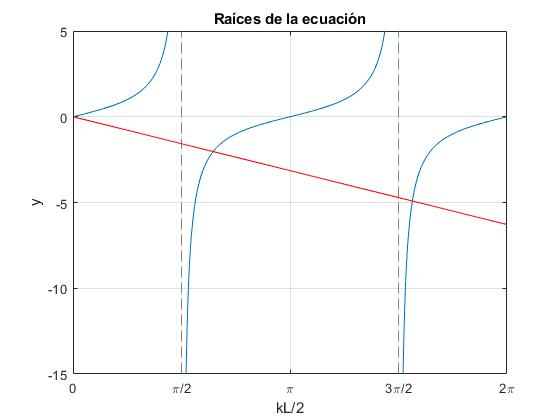
K pequeño: Para pequeños valores de la constante elástica del muelle, K, la pendiente a de la recta es grande y las raíces están próximas a los valores x para los que tan(x) se hace -∞: π/2, 3π/2, ... (2n+1)π/2.

${\displaystyle \begin{array}{l}kL=\frac{2n+1}{2}\pi ,n=\mathrm{0,1,2...}\\ 2L=\frac{2n+1}{2}{\lambda }_n\end{array}}$

Un muelle de constante K pequeña no afecta a la cuerda.

K grande: Cuando la constante del muelle K se incrementa, la pendiente a disminuye, y las raíces k_nL se incrementan. Cuando K tiende a infinito, a tiende a cero y las raíces k_nL tienden a π, 2π, ...nπ, donde la tangente se hace cero. Dado que la constante del muelle K es muy grande, la partícula de masa M situada en x=L permanecerá en reposo

${\displaystyle \begin{array}{l}kL=n\pi ,n=\mathrm{1,2...}\\ 2L=n{\lambda }_n\end{array}}$

Las frecuencias del modos impares se confunden con las frecuencias de los modos pares.

• Cuando K=0, el muelle desaparece y solamente queda la masa puntual M, que ya hemos estudiado en la la página titulada Modos de vibración de una cuerda con cuentas

Modos de vibración

• Para los modos pares k_nL=nπ, sin(k_nL)=0, D=0

${\displaystyle \begin{array}{l}\Phi (x)=\{\begin{array}{l}A\sin (kx)0\le x<L\\ C\sin (k(x-L))L\le x<2L\end{array}\\ \Phi (x)=\{A\sin (kx)0\le x<2L\end{array}}$

Determinamos el valor del coeficiente A de modo que

${\displaystyle {\displaystyle \underset{0}{\overset{2L}{\int }}{\Phi }_n^2(x)·dx=1}}$

El resultado de la inetgral es

${\displaystyle A^2{\displaystyle \underset{0}{\overset{2L}{\int }}{\sin }^2(kx)dx}=A^{2}L}$

• Para los modos impares, k_nL, son las raíces de la ecuación transcendente

Despejamos los coeficientes C y D en términos de A

D=Asin(kL)
C=-Acos(kL)

${\displaystyle \begin{array}{l}\Phi (x)=\{\begin{array}{l}A\sin (kx)0\le x<L\\ -A\cos (kL)\sin (k(x-L))+A\sin (kL)\cos (k(x-L))L\le x<2L\end{array}\hfill \\ \Phi (x)=\{\begin{array}{l}A\sin (kx)0\le x<L\\ A\sin (k(2L-x))L\le x<2L\end{array}\hfill \end{array}}$

Determinamos el valor del coeficiente A de modo que

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{2L}{\int }}{\Phi }_n^2(x)·dx=1}\\ A^2{\displaystyle \underset{0}{\overset{L}{\int }}{\sin }^2(kx)dx}+A^2{\displaystyle \underset{0}{\overset{L}{\int }}{\sin }^2\left(k(2L-x)\right)dx}=A^2\left(L-\frac{1}{2k}\sin (2kL)\right)\end{array}}$

Resolvemos la ecuación transcendente

${\displaystyle \begin{array}{l}\frac{M{k}^2{v}^2-K}{kT}\sin \left(kL\right)-2\cos \left(kL\right)=0\\ \left(\frac{M}{m}(kL)-\frac{KL}{T}\frac{1}{(kL)}\right)\sin \left(kL\right)-2\cos \left(kL\right)=0\end{array}}$

Utilizamos la función raices definida en el apartado titulado 'Raíces múltiples' de la página Funciones MATLAB para calcular las raíces de una ecuación, para calcularlas. Asignamos al cociente M/m=1 y al parámetro KL/T=0.5 relacionado con la constante del muelle K. M es la masa de la partícula y μ₀=m/L es la densidad lineal de la cuerda

En este script calculamos cinco modos de vibración mediante la primera fórmula, k_nL=nπ, cinco mediante la segunda (resolviendo la ecuación transcendente). Utilizamos la función sort de MATLAB para ordenar los diez primeros modos de vibración

r=(1:5)*pi; %par
M_m=1; %cociente M/m
K=0.5; %proporcional a la constante K del muelle
f=@(x) (M_m*x-K./x).*sin(x)-2*cos(x);
x=linspace(0,20,20);
k=raices(f,x); %impar
K=[k,r];
sort(K) %ordenados

    1.1984    3.1416    3.6581    6.2832    6.5814    
9.4248    9.6306   12.5664   12.7228   15.7080   15.8339   18.9548

Representamos los tres primeros modos de vibración para M/m=1 y KL/T=0.5

L=1; %longitud de la cuerda 2L
M_m=1; %relación entre masas
K=0.5; % porporcional a la constante del muelle K
f=@(x) (M_m*x-K./x).*sin(x)-2*cos(x);

subplot(3,1,1)
k=fzero(f,1);
hold on
area=L-sin(2*k*L)/(2*k);
fplot(@(x) sin(k*x)/sqrt(area),[0,L])
fplot(@(x) sin(k*(2*L-x))/sqrt(area),[L,2*L])
plot(L,sin(k*L)/sqrt(area),'ro','markersize',4,'markeredgecolor','r',
'markerfacecolor','r')
hold off
grid on
xlabel('x')
ylabel('\Phi')
title(sprintf('k=%1.2f',k))

k=pi/L;
subplot(3,1,2)
hold on
fplot(@(x) sin(k*x),[0,2*L])
plot(L,0,'ro','markersize',4,'markeredgecolor','r','markerfacecolor','r')
hold off
grid on
xlabel('x')
ylabel('\Phi')
title(sprintf('k=%1.2f',pi/L))

k=fzero(f,4);
subplot(3,1,3)
hold on
area=L-sin(2*k*L)/(2*k);
fplot(@(x) sin(k*x)/sqrt(area),[0,L])
fplot(@(x) sin(k*(2*L-x))/sqrt(area),[L,2*L])
plot(L,sin(k*L)/sqrt(area),'ro','markersize',4,'markeredgecolor','r',
'markerfacecolor','r')
hold off
grid on
xlabel('x')
ylabel('\Phi')
title(sprintf('k=%1.2f',k))

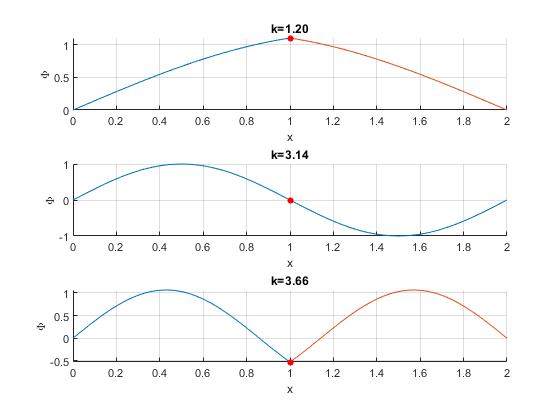
Observamos que para los modos impares, la función Φ(x) es continua y también su derivada. La partícula pernanece en reposo, no vibra, en un nodo. Para los modos pares, la función Φ(x) es continua pero no lo es su derivada, la partícula oscila.

El resonador en cualquier posición

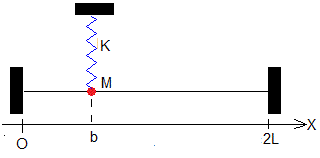
Consideremos ahora que la partícula de masa M unida al muelle elástico de constante K (el resonador) está situado en la posición b, en la mitad izquerda de la cuerda. Veremos que esto afecta a las frecuencias de los modos de vibración de orden par e impar y como se modifica el aspecto de los modos normales de vibración.

La segunda ley de Newton aplicada a la partícula de masa M se escribe

${\displaystyle \left({\left(T\frac{\partial y}{\partial x}\right)}_{b+}-{\left(T\frac{\partial y}{\partial x}\right)}_{b-}\right)-Ky=M\frac{{\partial }^{2}y}{\partial t^2}}$

Escribimos la solución de la ecuación diferencial en derivadas parciales como producto, y(x,t)=Φ(x)·cos(ωt)

${\displaystyle \begin{array}{l}\frac{d}{dx}\left(\frac{d\Phi }{dx}T(x)\right)+\mu {\omega }^2\Phi =0\\ \left({\left(T\frac{d\Phi }{dx}\right)}_{b+}-{\left(T\frac{d\Phi }{dx}\right)}_{b-}\right)-K\Phi +M{\omega }^2\Phi =0\end{array}}$

Consideramos que la tensión T(x)=T de la cuerda es constante, su densidad μ₀=m/L es constante.

${\displaystyle \begin{array}{l}\frac{d^2\Phi }{d{x}^2}+k^2\Phi =0\\ \omega =k\sqrt{\frac{T}{{\mu }_0}}=kv\end{array}}$

El término, bajo la raíz cuadrada es la velocidad de propagación de las ondas transversales en una cuerda.

La solución de esta ecuación diferencial tiene la forma conocida, Asin(kx)+Bcos(kx). Probamos la solución

${\displaystyle \Phi (x)=\{\begin{array}{l}A\sin (kx)+B\cos (kx)0\le x<b\\ C\sin \left(k(x-b)\right)+D\cos \left(k(x-b)\right)b\le x<2L\end{array}}$

Los extremos de la cuerda x=0 y x=2L son fijos. Φ(0)=0 y Φ(2L)=0, por lo que el coeficiente B=0 y se cumplirá que, Csin(k(2L-b))+Dcos(k(2L-b))=0

${\displaystyle \Phi (x)=\{\begin{array}{l}A\sin (kx)0\le x<b\\ C\sin \left(k(x-b)\right)+D\cos \left(k(x-b)\right)b\le x<2L\end{array}}$

En x=b se ha situado una masa puntual M, la función Φ(x) es continua en este punto

Asin(kL)=D

De estas dos relaciones despejamos C en función de A

${\displaystyle C=-A\frac{\sin (kb)\cos \left(k(2L-b)\right)}{\sin \left(k(2L-b)\right)}}$

Cuando el resonador está situado en un nodo, sin(kb)=0 y también sin(k(2L-b))=0. Tenemos una indeterminación 0/0. En este caso, C=Acos(2L-b))·(-1)ⁿ, siendo n el modo de vibración de orden n. Para b=L punto medio de la cuerda, C=-Acos(kL), tal como hemos visto en el apartado anterior.

Modos de vibración

Obtenemos la siguiente ecucación transcendente

${\displaystyle \begin{array}{l}\left({\left(\frac{d\Phi }{dx}\right)}_{b+}-{\left(\frac{d\Phi }{dx}\right)}_{b-}\right)-\frac{K}{T}\Phi (b)+\frac{M}{T}{\omega }^2\Phi (b)=0\\ Ck-Ak\cos \left(kb\right)-\frac{K}{T}A\sin \left(kb\right)+\frac{M}{T}{\omega }^{2}A\sin \left(kb\right)=0\\ -\frac{\sin (kb)\cos \left(k(2L-b)\right)}{\sin \left(k(2L-b)\right)}-\cos \left(kb\right)+\frac{M{k}^2{v}^2-K}{kT}\sin \left(kb\right)=0\\ \frac{M{k}^2{v}^2-K}{kT}\frac{\sin (kb)\sin \left(k(2L-b)\right)}{\sin \left(2kL\right)}=1\end{array}}$

Expresamos la ecuación transcendente de la forma

${\displaystyle \left(\frac{M}{m}(kL)-\frac{KL}{T}\frac{1}{(kL)}\right)\sin \left(kL\frac{b}{L}\right)\sin \left(kL\left(2-\frac{b}{L}\right)\right)-2\sin \left(kL\right)\cos \left(kL\right)=0}$

Representamos esta función f(kL) para darnos cuenta de las dificultades del procedimiento del punto medio para calcular algunas raíces de esta ecuación transcendente. La función es casi tangente al eje X para ciertos valores de kL

L=1; %longitud
M_m=1; %relación entre masas
K=1; % porporcional a la constante del muelle K
b=2/3; %b/L posición del resonador
f=@(x) (M_m*x-K./x).*(sin(x*b).*sin(x*(2-b)))-sin(2*x);
fplot(f,[0,20])
grid on
xlabel('kL')
ylabel('f')
title('Raíces de la ecuación transcendente')

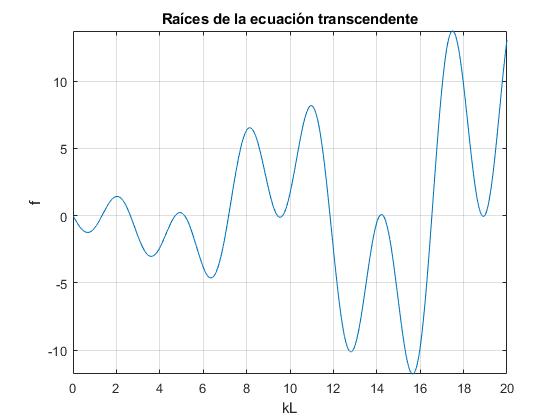
Cuando b=L. Obtenemos la relación estudiada en el primer apartado

${\displaystyle \sin (kL)\left\{\frac{M{k}^2{v}^2-K}{kT}\sin (kL)-2\cos (kL)\right\}=0}$

Para representar el modo de vibración n, Φ_n(x) los coeficientes C y D dependen de A. Fijamos A de modo que

${\displaystyle {\displaystyle \underset{0}{\overset{2L}{\int }}{\Phi }_n^2(x)·dx=1}}$

El resultado de calcular las integrales es

${\displaystyle \begin{array}{l}{A}^2{\displaystyle \underset{0}{\overset{b}{\int }}{\sin }^2(kx)dx}+{\displaystyle \underset{b}{\overset{2L}{\int }}{\left(C\sin \left(k(x-b)\right)+D\cos \left(k(x-b)\right)\right)}^{2}dx=1}\\ A^2{\displaystyle \underset{0}{\overset{b}{\int }}{\sin }^2(kx)dx}+C^2{\displaystyle \underset{b}{\overset{2L}{\int }}{\sin }^2\left(k(x-b)\right)dx}+D^2{\displaystyle \underset{b}{\overset{2L}{\int }}{\cos }^2\left(k(x-b)\right)dx}+CD{\displaystyle \underset{b}{\overset{2L}{\int }}\sin \left(2k(x-b)\right)dx}=1\\ \frac{A^2}{2}\left(b-\frac{1}{2k}\sin \left(2kb\right)\right)+\frac{C^2}{2}\left(2L-b-\frac{1}{2k}\sin \left(2k(2L-b)\right)\right)+\frac{D^2}{2}\left(2L-b+\frac{1}{2k}\sin \left(2k(2L-b)\right)\right)+\frac{CD}{2k}\left(1-\cos \left(2k(2L-b)\right)\right)=1\end{array}}$

L=1; %longitud
M_m=1; %relación entre masas
K=1; % porporcional a la constante del muelle K
b=0.5; %b/L posición del resonador
f=@(x) (M_m*x-K./x).*(sin(x*b).*sin(x*(2-b)))-sin(2*x);
x=linspace(0,20,50);
r=raices(f,x); %impar

for i=1:4
    subplot(4,1,i)
    k=r(i);
    if sin(k*b)<1e-5
        C=cos(k*(2-b))*(-1)^i;
    else     
        C=-sin(k*b)*cos(k*(2-b))/sin(k*(2-b));
    end
    D=sin(k*b);
    area=(b-sin(2*k*b)/(2*k))/2+C^2*(2*L-b-sin(2*k*(2*L-b))/(2*k))/2+
C*D*(1-cos(2*k*(2*L-b)))/(2*k)+D^2*(2*L-b+sin(2*k*(2*L-b))/(2*k))/2;
    hold on
    fplot(@(x) sin(k*x/L)/sqrt(area),[0,b*L])
    fplot(@(x) (C*sin(k*(x/L-b))+D*cos(k*(x/L-b)))/sqrt(area),[b*L, 2*L])
    plot(b*L,sin(k*b)/sqrt(area),'ro','markersize',4,'markeredgecolor',
'r','markerfacecolor','r')
    hold off
    grid on
    xlabel('x')
    ylabel('\Phi')
    title(sprintf('k=%1.2f',k))
end

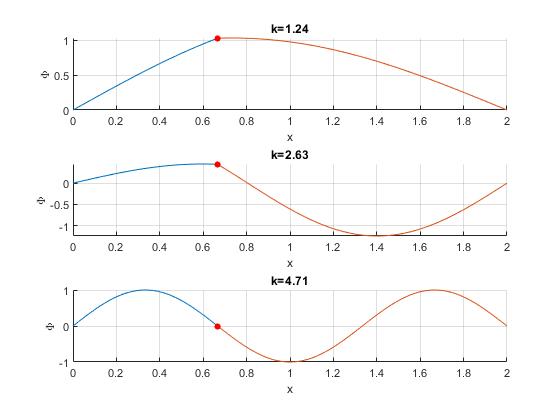
• En el segundo modo de vibración, la cuerda presenta un nodo (no vibra) en la mitad de la cuerda 2L/2=L. Si situamos el resonador en b=L, la cuerda no se verá afectada. Se ha estudiado en el apartado anterior

• En el tercer modo de vibración, la cuerda presenta nodos en los puntos 2L/3 y 4L/3. Si situamos el resonador en b=2L/3, la cuerda no se verá afectada.

• ...

Actividades

Se introduce

• El cociente de masas M/m (masa puntual dividido por la masa de una porción de la cuerda de longitud L) en el control titulado Masa M/m

• El valor del parámetro KL/T donde K es la constante elástica del muelle y T la tensión de la cuerda, en el control titulado Parámetro

• La posición b del resonador, en la mitad izquierda de la cuerda, en el control titulado Posición resonador. (En la mitad derecha, daría los mismos resultados)

• La longitud de la porción L de cuerda se ha fijado en L=1 m

• La velocidad de propagación de las ondas trasversales en la cuerda se ha fijado en v=1 m/s. El valor numérico del número de onda k coincide con el valor de la frecuencia angular ω, la frecuencia de los distintos modos de vibración f=ω/(2π)

Se pulsa el botón titulado Nuevo

Se pulsa el botón titulado >>, para observar el siguiente modo de vibración.

Se pulsa el botón titulado <<, para observar el modo de vibración anterior

En la parte superior, se muestra el modo de vibración y su frecuencia f en Hz.

Para ver los modos de vibración descritos en el primer apartado de esta página, introducir en el control titulado Posición resonador, b=1. Otras posiciones del resonador en los nodos son b=2/3≈0.6667, 0.5, 0.25, ... Debido a la dificultad antes mencionada, para encontrar las raíces de la ecuación transcendente, el programa interactivo puede no dar buenos resultados para posiciones del resonador en otros nodos

Referencias

V. Migulin. V. Medvedev. E. Mustel. V. Parygin. Basic theory of oscillations. Mir Publishers Moscow. 1983. pp. 330-335.