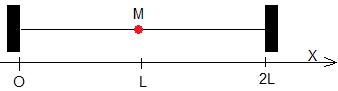
Sea una cuerda de longitud 2L y densidad lineal μ₀=m/L, sujeta por ambos extremos, cuya tensión es T en la que se colocado una masa puntual (una cuenta) M en su punto medio.

Fuerza sobre un elemento diferencial de cuerda

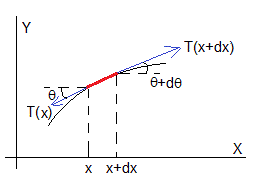
Consideremos una porción de cuerda comprendida entre x y x+dx

• T(x), es la fuerza que ejerce la parte izquierda de la cuerda sobre el elemento diferencial

• T(x+dx), es la fuerza que ejerce la parte derecha de la cuerda sobre el elemento diferencial

La componente Y de las fuerzas, dF_y, que actúan sobre dicho elemento diferencial es

${\displaystyle \begin{array}{l}d{F}_y=T(x+dx)·\sin (\theta +d\theta )-T(x)\sin \theta \simeq \hfill \\ \left(T(x)+\frac{dT}{dx}dx\right)·(\sin \theta +\cos \theta ·d\theta )-T(x)\sin \theta =\hfill \\ \frac{d}{dz}\left(\sin \theta ·T(x)\right)·dx\simeq \frac{d}{dz}\left(\tan \theta ·T(x)\right)·dx=\frac{d}{dx}\left(\frac{dy}{dx}·T(x)\right)·dx\hfill \end{array}}$

Para ángulos pequeños, hacemos la aproximación sinθ≈tanθ

Esta componente dF_y de fuerza sobre el elemento diferencial de masa μ(x)dx produce una aceleración a lo largo del eje Y. Teniendo en cuenta, y es una función continua de x y t escribimos, la segunda ley de Newton, fuerza=masa×aceleración

${\displaystyle \begin{array}{l}\frac{\partial }{\partial x}\left(\frac{\partial y}{\partial x}T(x)\right)dx=\left(\mu ·dx\right)\frac{{\partial }^{2}y}{\partial t^2}\\ \frac{\partial }{\partial x}\left(\frac{\partial y}{\partial x}T(x)\right)=\mu \frac{{\partial }^{2}y}{\partial t^2}\end{array}}$

Donde μ(x) es la densidad de una cuerda no homogénea y T(x) es la tensión en cada punto de la cuerda

y(x,t) es una función continua de x y su derivada dy/dx también lo es.

Fuerza sobre una masa puntual situada en la cuerda

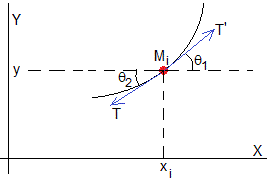
Consideremos una masa puntual M_i sujeta a la cuerda en la posición x_i

Como vemos en la figura, en un instante t, la función y(x) es continua pero no su derivada dy/dx en x_i

La componente Y de las fuerzas, F_y, que actúan sobre dicha partícula es

${\displaystyle F_y=T\sin {\theta }_2-T\text{'}\sin {\theta }_1\approx T\tan {\theta }_2-T\text{'}\tan {\theta }_1=\left({\left(T\frac{\partial y}{dx}\right)}_{x_i+}-{\left(T\frac{\partial y}{dx}\right)}_{x_i-}\right)}$

T es la fuerza que ejerce la parte izquierda de la cuerda sobre la partícula y T' es la fuerza que ejerce la parte derecha de la cuerda sobre la partícula. θ₁ y θ₂ son las direcciones de dichas fuerzas, tangentes a la cuerda en el punto x_i

La segunda ley de Newton a lo largo del eje Y se escribe

${\displaystyle \left({\left(T\frac{\partial y}{\partial x}\right)}_{x_i+}-{\left(T\frac{\partial y}{\partial x}\right)}_{x_i-}\right)=M_i\frac{{\partial }^{2}y}{\partial t^2}}$

Modos de vibración de una cuerda con una cuenta

Escribimos la solución de la ecuación diferencial en derivadas parciales como producto, y(x,t)=Φ(x)·cos(ωt)

${\displaystyle \begin{array}{l}\frac{d}{dx}\left(\frac{d\Phi }{dx}T(x)\right)+\mu {\omega }^2\Phi =0\\ \left({\left(T\frac{d\Phi }{dx}\right)}_{L+}-{\left(T\frac{d\Phi }{dx}\right)}_{L-}\right)+M{\omega }^2\Phi =0\end{array}}$

Consideramos que la tensión T(x)=T de la cuerda es constante, su densidad μ₀=m/L es constante y la posición de la cuenta de masa M es x_i=L.

${\displaystyle \begin{array}{l}\frac{d^2\Phi }{d{x}^2}+k^2\Phi =0\\ \omega =k\sqrt{\frac{T}{{\mu }_0}}\end{array}}$

El término, bajo la raíz cuadrada es la velocidad de propagación de las ondas transversales en una cuerda. La solución de esta ecuación diferencial tiene la forma conocida, Asin(kx)+Bcos(kx)

La masa puntual M situada en la posición x=L, divide a la cuerda en dos partes. Probamos la solución

${\displaystyle \Phi (x)=\{\begin{array}{l}A\sin (kx)+B\cos (kx)0\le x<L\\ C\sin \left(k(x-L)\right)+D\cos \left(k(x-L)\right)L\le x<2L\end{array}}$

• Los extremos de la cuerda x=0 y x=2L son fijos. Φ(0)=0 y Φ(2L)=0, por lo que el coeficiente B=0 y se cumplirá que, Csin(kL)+Dcos(kL)=0

${\displaystyle \Phi (x)=\{\begin{array}{l}A\sin (kx)0\le x<L\\ C\sin \left(k(x-L)\right)+D\cos \left(k(x-L)\right)L\le x<2L\end{array}}$

• En x=L se ha situado una masa puntual M, la función Φ(x) es continua en este punto

Asin(kL)=D

Con la relación anterior entre los coeficientes C y D,

${\displaystyle \sin (kL)\left(C+A\cos (kL)\right)=0}$

Una solución es

sin(kL)=0, k_nL=nπ, n=1,2,3...

Sabiendo que k=2π/λ, 2L=nλ_n, un número entero de longitudes de onda cabe en la cuerda de longitud 2L sujeta por ambos extremos, estas son los modos normales de vibración pares de la cuerda

La otra solución es, C=-Acos(kL)

• Por otra parte, la función Φ(x) ha de satisfacer la condición

${\displaystyle \begin{array}{l}\left({\left(\frac{d\Phi }{dx}\right)}_{L+}-{\left(\frac{d\Phi }{dx}\right)}_{L-}\right)+\frac{M}{T}{\omega }^2\Phi (L)=0\\ Ck-Ak\cos \left(kL\right)+\frac{M}{T}{\omega }^{2}A\sin \left(kL\right)=0\\ -Ak\cos (kL)-Ak\cos \left(kL\right)+\frac{M}{T}{\omega }^{2}A\sin \left(kL\right)=0\\ \frac{M}{m}\left(kL\right)\sin \left(kL\right)-2\cos \left(kL\right)=0\end{array}}$

Donde ω=kv, la velocidad de propagación v²=T/μ₀, la densidad lineal de la cuerda μ₀=m/L. 2m es la masa de la cuerda de longitud 2L

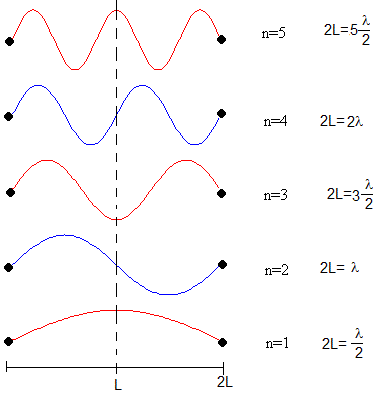
En la figura, se muestran los modos de vibración de una cuerda de longitud 2L. Los modos de vibración de orden par n=2,4,6,... presentan un nodo en x=L

Por tanto, los valores de k_nL se obtienen de dos ecuaciones

• sin(kL)=0, cuya solución es

k_nL=nπ, n=1,2,3,...

2L=nλ. Estos son los modos de vibración de orden par que no resultan modificados por la presencia de la cuenta, ya que está situada en un nodo

• Para los modos de vibración de orden impar, calculamos las raíces k_nL de la ecuación transcendente

${\displaystyle \frac{M}{m}(kL)\sin (kL)-2\cos \left(kL\right)=0}$

• Para los modos pares k_nL=nπ, sin(k_nL)=0, D=0

${\displaystyle \begin{array}{l}\Phi (x)=\{\begin{array}{l}A\sin (kx)0\le x<L\\ C\sin (k(x-L))L\le x<2L\end{array}\\ \Phi (x)=\{A\sin (kx)0\le x<2L\end{array}}$

• Para los modos impares k_nL raíces de la ecuación transcendente

Despejamos los coeficientes C y D en términos de A

D=Asin(kL)
C=-Acos(kL)

${\displaystyle \begin{array}{l}\Phi (x)=\{\begin{array}{l}A\sin (kx)0\le x<L\\ -A\cos (kL)\sin (k(x-L))+A\sin (kL)\cos (k(x-L))L\le x<2L\end{array}\hfill \\ \Phi (x)=\{\begin{array}{l}A\sin (kx)0\le x<L\\ A\sin (k(2L-x))L\le x<2L\end{array}\hfill \end{array}}$

Representamos la función $f(x)=\frac{M}{m}x\sin (x)-2\cos \left(x\right)$, para el valor M/m=1. Se sugiere cambiar este valor para apreciar el efecto de la masa M de la partícula

L=1; %longitud
M_m=1; %cociente masas

f=@(x) M_m*x.*sin(x)-2*cos(x);
fplot(f,[0,10])
grid on
xlabel('kL')
ylabel('y');
title('Cuerda con una cuenta')

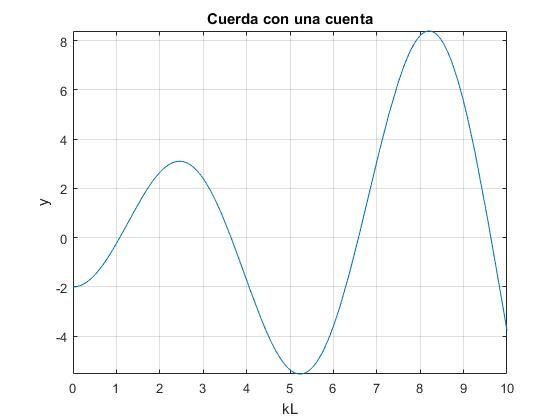
Las raíces son los puntos de corte con el eje X. Utilizamos la función raices definida en el apartado titulado 'Raíces múltiples' de la página Funciones MATLAB para calcular las raíces de una ecuación, para calcularlas. Asignamos al cociente M/m=1. Donde M es la masa de la partícula y μ₀=m/L es la densidad lineal de la cuerda

M_m=1; %cociente M/m
f=@(x) M_m*x.*sin(x)-2*cos(x);
x=linspace(0,20,20);
k=raices(f,x); % raíces
disp(k);

    1.0769    3.6436    6.5783    9.6296   12.7223   15.8336   18.9547

Modos de vibración

• Modos pares

${\displaystyle \begin{array}{l}{\Phi }_n(x)=A\sin (k_{n}x)0\le x<2L\\ k_n=\frac{n\pi }{L},n=\mathrm{1,2,3...}\end{array}}$

Determinamos el valor del coeficiente A de modo que

${\displaystyle {\displaystyle \underset{0}{\overset{2L}{\int }}{\Phi }_n^2(x)·dx=1}}$

El resultado de la integral es

${\displaystyle A^2{\displaystyle \underset{0}{\overset{2L}{\int }}{\sin }^2(kx)dx}=A^{2}L}$

• Modos impares

${\displaystyle {\Phi }_n(x)=\{\begin{array}{l}A\sin (k_{n}x)0\le x<L\\ A\sin \left(k_n(2L-x)\right)L\le x<2L\end{array}}$

k_nL son las raíces de la ecuación transcendente

Determinamos el valor del coeficiente A de modo que

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{2L}{\int }}{\Phi }_n^2(x)·dx=1}\\ A^2{\displaystyle \underset{0}{\overset{L}{\int }}{\sin }^2(kx)dx}+A^2{\displaystyle \underset{0}{\overset{L}{\int }}{\sin }^2\left(k(2L-x)\right)dx}=A^2\left(L-\frac{1}{2k}\sin (2kL)\right)\end{array}}$

Resolvemos la ecuación transcendente

${\displaystyle \frac{M}{m}(kL)\sin (kL)-2\cos \left(kL\right)=0}$

En este script calculamos cinco modos de vibración mediante la primera fórmula, cinco mediante la segunda y utilizamos la función sort de MATLAB para ordenar los diez primeros modos de vibración

r=(1:5)*pi; %par
M_m=1; %cociente M/m
f=@(x) M_m*x.*sin(x)-2*cos(x);
x=linspace(0,15,10);
k=raices(f,x); %impar
K=[k,r];
sort(K) %ordenados

ans =  1.0769    3.1416    3.6436    6.2832    6.5783    9.4248    9.6296  
 12.5664  12.7223   15.7080

Calculamos las raíces de forma gráfica

${\displaystyle \tan \left(kL\right)=\frac{2m}{M}\frac{1}{kL}}$

Las raíces k_nL son la intersección de la función y=tan(x) y de la hipérbola y=a/x.

hold on
fplot(@(x) tan(x), [0, 2*pi])
fplot(@(x) 1./x, [0,2*pi])
hold off
ylim([-2,15])
set(gca,'XTick',0:pi/2:2*pi)
set(gca,'XTickLabel',{'0','\pi/2','\pi','3\pi/2','2\pi'})
grid on
xlabel('kL/2')
ylabel('y')
title('Raíces de la ecuación')



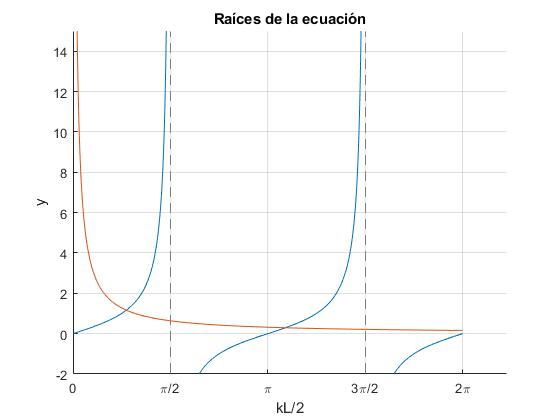
Cuando la masa M de la partícula es muy grande, el parámetro a es muy pequeño y las raíces k_nL del tercero, quinto, etc. modo de vibración tienden a π, 2π, 3π, ...

${\displaystyle \begin{array}{l}kL=(n-1)\pi ,n=\mathrm{2,3,4....}\\ 2L=(n-1){\lambda }_n\end{array}}$

La frecuencia del primer modo es cada vez más pequeña a medida que la masa de la partícula M aumenta. La frecuencia de los modos impares tiende hacia la frecuencia de los modos pares

Cuando M/m es grande, por ejemplo, M/m=10. La frecuencia del segundo y tercer modo casi coinciden, lo mismo la del cuarto con el quinto, etc.

...
M_m=10; %cociente M/m
...

    0.4328    3.1416    3.2039    6.2832    6.3148    9.4248    
9.4459   12.5664   12.5823   15.7080

Representamos los tres primeros modos de vibración para M/m=1

L=1; %longitud
M_m=1; %relación entre masas
f=@(x) M_m*x.*sin(x)-2*cos(x);

subplot(3,1,1)
k=fzero(f,1);
area=L-sin(2*k*L)/(2*k);
hold on
fplot(@(x) sin(k*x)/sqrt(area),[0,L])
fplot(@(x) sin(k*(2*L-x))/sqrt(area),[L,2*L])
plot(L,sin(k*L)/sqrt(area),'ro','markersize',4,'markeredgecolor','r'
,'markerfacecolor','r')
hold off
grid on
xlabel('x')
ylabel('\Phi')
title(sprintf('k=%1.2f',k))

k=pi/L;
subplot(3,1,2)
hold on
fplot(@(x) sin(k*x),[0,2*L])
plot(L,0,'ro','markersize',4,'markeredgecolor','r','markerfacecolor','r')
hold off
grid on
xlabel('x')
ylabel('\Phi')
title(sprintf('k=%1.2f',pi/L))

k=fzero(f,4);
area=L-sin(2*k*L)/(2*k);
subplot(3,1,3)
hold on
fplot(@(x) sin(k*x)/sqrt(area),[0,L])
fplot(@(x) sin(k*(2*L-x))/sqrt(area),[L,2*L])
plot(L,sin(k*L)/sqrt(area),'ro','markersize',4,'markeredgecolor','r',
'markerfacecolor','r')
hold off
grid on
xlabel('x')
ylabel('\Phi')
title(sprintf('k=%1.2f',k))

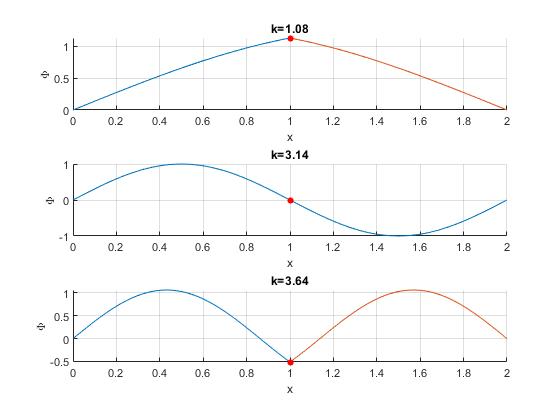
Observamos que para los modos impares, la función Φ(x) es continua y también su derivada. La partícula pernanece en reposo, no vibra, en un nodo. Para los modos pares, la función Φ(x) es continua pero no lo es su derivada, la partícula oscila.

Actividades

Se introduce

• El cociente de masas M/m (masa puntual dividido por la masa de una porción de la cuerda de longitud L) en el control titulado Masa M/m
• La longitud de la porción L de cuerda se ha fijado en L=1 m
• La velocidad de propagación de las ondas trasversales en la cuerda se ha fijado en v=1 m/s. El valor numérico del número de onda k coincide con el valor de la frecuencia angular ω, para calcular la frecuencia de los distintos modos de vibración f=ω/(2π)

Se pulsa el botón titulado Nuevo

Se pulsa el botón titulado >>, para observar el siguiente modo de vibración.

Se pulsa el botón titulado <<, para observar el modo de vibración anterior

En la parte superior, se muestra el modo de vibración y su frecuencia f en Hz.

Condiciones iniciales

La solución general y(x,t) que satisface la ecuación diferencial del movimiento ondulatorio

${\displaystyle \frac{T}{{\mu }_0}\frac{{\partial }^{2}y}{\partial x^2}=\frac{{\partial }^{2}y}{\partial t^2}}$

con las condiciones de contorno y(0,t)=0 e y(2L,t)=0 es

${\displaystyle y(x,t)={\displaystyle \sum _{n=1}^{\infty }{\Phi }_n(x)\left(A_n\cos \left({\omega }_{n}t\right)+B_n\sin \left({\omega }_{n}t\right)\right)}{\omega }_n=k_n\sqrt{\frac{T}{{\mu }_0}}}$

Esta ecuación describe todos los posibles modos de vibración de la cuerda. La vibración particular que experimenta la cuerda está únicamente determinada por las condiciones iniciales, que a su vez determinan los valores de las constantes A_n y B_n.

${\displaystyle \begin{array}{l}y(x\mathrm{,0})=y_0(x)\to {\displaystyle \sum _{n=1}^{\infty }{A}_n{\Phi }_n(x)}=y_0(x)\hfill \\ {\frac{\partial y(x,t)}{\partial t}|}_{t=0}={\dot{y}}_0(x)\to {\displaystyle \sum _{n=1}^{\infty }{\omega }_n{B}_n{\Phi }_n(x)}={\dot{y}}_0(x)\hfill \end{array}}$

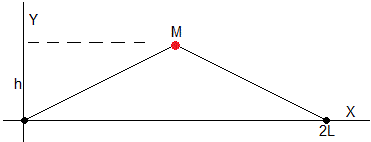
Supongamos que la cuerda se estira desde su punto medio donde se encuentra la cuenta, hasta adoptar la forma inicial la siguiente.

${\displaystyle y(x\mathrm{,0})=\{\begin{array}{l}\frac{h}{L}x0\le x<L\\ -\frac{h}{L}x+2hL\le x<2L\end{array}}$

Como velocidad inicial de la cuerda es nula, los coeficientes B_n=0.

Las relaciones de ortogonalidad de Φ_n(x) para una cuerda no homogénea de densidad μ(x)

${\displaystyle {\displaystyle \underset{0}{\overset{2L}{\int }}\mu (x){\Phi }_m(x)}{\Phi }_n(x)dx=0m\ne n}$

Para una cuerda homogénea de densidad μ₀ con una cuenta de masa M situada en x=L se escribe

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{L-}{\int }}{\mu }_0{\Phi }_m(x)}{\Phi }_n(x)dx+{\displaystyle \underset{L-}{\overset{L+}{\int }}\mu (x){\Phi }_m(x)}{\Phi }_n(x)dx+{\displaystyle \underset{L+}{\overset{2L}{\int }}{\mu }_0{\Phi }_m(x)}{\Phi }_n(x)dx=\\ {\mu }_0{\displaystyle \underset{0}{\overset{L-}{\int }}{\Phi }_m(x)}{\Phi }_n(x)dx+M{\Phi }_n(L){\Phi }_m(L)+{\mu }_0{\displaystyle \underset{L+}{\overset{2L}{\int }}{\Phi }_m(x)}{\Phi }_n(x)dx=0\\ {\mu }_0{\displaystyle \underset{0}{\overset{2L}{\int }}{\Phi }_m(x)}{\Phi }_n(x)dx+M{\Phi }_n(L){\Phi }_m(L)=0m\ne n\end{array}}$

Nota: Formalmente, la densidad de la cuerda uniforme con una cuenta en x=L se escribe

$\begin{array}{l}\mu (x)={\mu }_0+M\delta (x-L)\\ {\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\delta (x-L)f(x)dx=f(L)}\end{array}$

Véase la función delta de Dirac δ(x) al final de la página titulada Transformada de Fourier

Utilizamos la relación de ortogonalidad de las funciones Φ_n(x) y Φ_m(x) para calcular los coeficientes A_n

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{2L}{\int }}\mu (x)}{y}_0(x){\Phi }_n(x)dx={\displaystyle \sum _{m=1}^{\infty }{A}_m{\displaystyle \underset{0}{\overset{2L}{\int }}\mu (x){\Phi }_m(x){\Phi }_n(x)dx}}\\ {\displaystyle \underset{0}{\overset{2L}{\int }}\mu (x)}{y}_0(x){\Phi }_n(x)dx=A_n{\displaystyle \underset{0}{\overset{2L}{\int }}\mu (x){\Phi }_n^2(x)dx}\\ {\mu }_0{\displaystyle \underset{0}{\overset{2L}{\int }}{y}_0(x){\Phi }_n(x)dx}+M{y}_0(L){\Phi }_n(L)=A_n\left\{{\mu }_0{\displaystyle \underset{0}{\overset{2L}{\int }}{\Phi }_n^2(x)dx+M{\Phi }_n^2(L)}\right\}\end{array}}$

• Primero, calculamos A_n cuando k_nL es un múltiplo entero de π, sin(k_nL)=0, Φ_n(x)=Asin(k_nx), 0≤x<2L

${\displaystyle \begin{array}{l}\frac{m}{L}{\displaystyle \underset{0}{\overset{L}{\int }}\left(\frac{h}{L}x\right)}A\sin (k_{n}x)dx+\frac{m}{L}{\displaystyle \underset{L}{\overset{2L}{\int }}\left(-\frac{h}{L}x+2h\right)}A\sin (k_{n}x)dx+MhA\sin (k_{n}L)=\\ A_n\left\{{\displaystyle \underset{0}{\overset{2L}{\int }}{A}^2{\sin }^2(k_{n}x)dx}+M{A}^2{\sin }^2(k_{n}L)\right\}\end{array}}$

Utilizamos la integral por partes

${\displaystyle {\displaystyle \int x\sin (kx)dx}=-\frac{x}{k}\cos (kx)+\frac{1}{k^2}\sin (kx)}$

El resultado final es A_n=0

• Calculamos A_n cuando k_nL es una raíz de la ecuación transcendente

${\displaystyle \frac{M}{m}(kL)\sin (kL)-2\cos \left(kL\right)=0}$

y Φ_n(x) es la función

${\displaystyle {\Phi }_n(x)=\{\begin{array}{l}A\sin (k_{n}x)0\le x<L\\ -A\sin \left(k_n(x-2L)\right)L\le x<2L\end{array}}$

Realizamos las operaciones siguientes

${\displaystyle \begin{array}{l}\frac{m}{L}{\displaystyle \underset{0}{\overset{L}{\int }}\left(\frac{h}{L}x\right)}A\sin (k_{n}x)dx+\frac{m}{L}{\displaystyle \underset{L}{\overset{2L}{\int }}\left(-\frac{h}{L}x+2h\right)}(-A)\sin \left(k_n(x-2L)\right)dx+MhA\sin (k_{n}L)=\\ A_n\left\{{\displaystyle \underset{0}{\overset{L}{\int }}{A}^2{\sin }^2(k_{n}x)dx}+{\displaystyle \underset{L}{\overset{2L}{\int }}{A}^2{\sin }^2\left(k_n(x-2L)\right)dx}+\left(k_n(x-2L)\right)M{A}^2{\sin }^2(k_{n}L)\right\}\end{array}}$

Utilizamos la integral por partes y la ecuación transcendente, el resultado final es

${\displaystyle A_n=\frac{1}{A}\frac{2h}{{\left(k_{n}L\right)}^2\left(1+\frac{M}{2m}\sin \left(k_{n}L\right)\right)}}$

La forma de la cuerda es en el instante t es

${\displaystyle \begin{array}{l}y(0\le x<L,t)={\displaystyle \sum _{n=1}^{\infty }\frac{2h}{{\left(k_{n}L\right)}^2\left(1+\frac{M}{2m}\sin \left(k_{n}L\right)\right)}\sin (k_{n}x)\cos \left({\omega }_{n}t\right)}\\ y(L\le x<2L,t)=-{\displaystyle \sum _{n=1}^{\infty }\frac{2h}{{\left(k_{n}L\right)}^2\left(1+\frac{M}{2m}\sin \left(k_{n}L\right)\right)}\sin \left(k_n(x-2L)\right)\cos \left({\omega }_{n}t\right)}\\ {\omega }_n=k_n\sqrt{\frac{T}{{\mu }_0}}\end{array}}$

k_nL son las raíces de la ecuación transcendente.

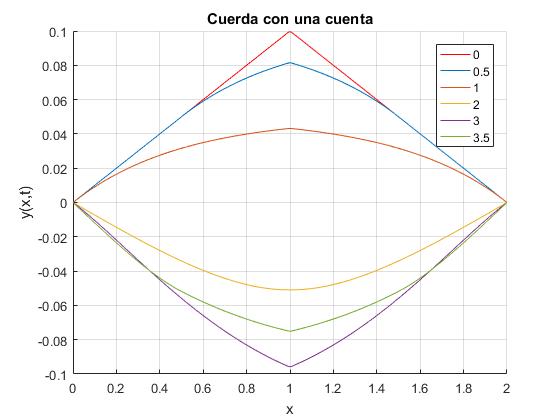
Elaboramos un script, para representar la forma de la cuerda con una cuenta en su punto medio, para varios instantes. La longitud de la cuerda 2L= 2, la deformación máxima de la cuerda es h=0.1 y la relación de masas M/m=1. (M es la masa de la partícula y μ₀=m/L la densidad lineal de la cuerda). Se sugiere cambiar este parámetro y observar sus efectos por ejemplo, para M/m=0.5 y M/m=2.

El periodo o tiempo que tarda en viajar una perturbación desde un extremo a otro de la cuerda y regresar al punto de partida es τ=4L/v. Donde v=1 es la velocidad de propagación. Representamos la forma de la cuerda en los instantes t/τ=0 (forma inicial), 0.5, 1, 2, 3, 3.5

M_m=1;%relación entre masas M/m
L=1; %longitud de la cuerda
h=0.1; %deformación de la cuerda

f=@(x) M_m*x.*sin(x)-2*cos(x);
x=linspace(0.1,60,50);
k=raices(f,x); %20 raíces
An=2*h*sin(k*L)./(((k*L).^2).*(1+M_m*sin(k*L).^2/2)); %coeficientes

hold on
x=linspace(0,2*L,200);
%forma inicial
y=(h*x/L).*(heaviside(x)-heaviside(x-L))+(2*h*(1-x/(2*L))).*
(heaviside(x-L)-heaviside(x-2*L));
plot(x,y, 'r','displayName',num2str(0))

for t=[0.5,1,2,3,3.5]
    yy=zeros(1,length(x)); 
    for n=1:length(k)
        yy=yy+An(n)*(sin(k(n)*(x<=L).*x)-sin(k(n)*(x>L).*(x-2*L)))*cos(k(n)*t/L);
    end
    plot(x,yy, 'displayName',num2str(t))
end
hold off
grid on
legend('-DynamicLegend','location','northeast')
xlabel('x')
ylabel('y(x,t)')
title('Cuerda con una cuenta')

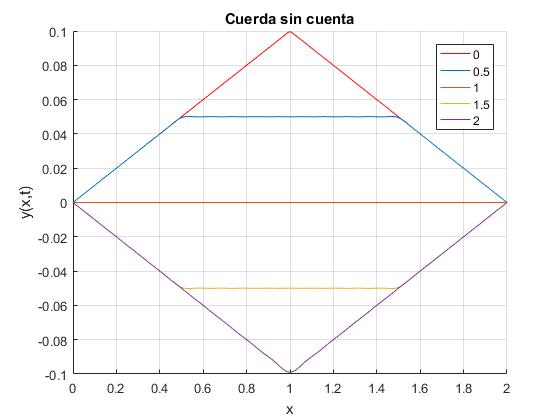
Modificamos el script para representar la forma de la cuerda sin cuenta M/m=0, en los instantes t/τ=0 (forma inicial), 0.5, 1, 1.5, 2. Comprobamos que vuelve a la forma inicial en el instante t/τ=4

Actividades

Se introduce

• El cociente de masas M/m (masa puntual dividido por la masa de una porción de la cuerda de longitud L) en el control titulado Masa M/m
• La longitud de la porción L de cuerda se ha fijado en L=1 m
• La velocidad de propagación de las ondas trasversales en la cuerda se ha fijado en v=1 m/s.

Se pulsa el botón titulado Nuevo

Dos partículas sujetas a la cuerda

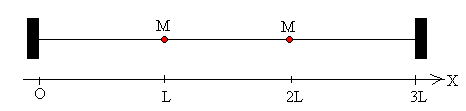
Consideremos una cuerda homogénea de longitud 3L y densidad uniforme m/L con dos masas puntuales M situadas en las posiciones x=L y x=2L tal como se muestra en la figura.

Las masas puntuales M situadas en la posiciones x=L y x=2L, dividen a la cuerda en tres partes. Probamos la solución

${\displaystyle \Phi (x)=\{\begin{array}{l}A\sin (kx)+B\cos (kx)0\le x<L\\ C\sin \left(k(x-L)\right)+D\cos \left(k(x-L)\right)L\le x<2L\\ E\sin \left(k(x-2L)\right)+F\cos \left(k(x-2L)\right)2L\le x<3L\end{array}}$

• Los extremos de la cuerda x=0 y x=3L son fijos. Φ(0)=0 y Φ(3L)=0, por lo que el coeficiente B=0, y se cumplirá que Esin(kL)+Fcos(kL)=0

${\displaystyle \Phi (x)=\{\begin{array}{l}A\sin (kx)0\le x<L\\ C\sin \left(k(x-L)\right)+D\cos \left(k(x-L)\right)L\le x<2L\\ E\sin \left(k(x-2L)\right)+F\cos \left(k(x-2L)\right)2L\le x<3L\end{array}}$

• En x=L se ha situado una masa puntual M, la función Φ(x) es continua en este punto

Asin(kL)=D

• Por otra parte, la función Φ(x) ha de satisfacer la condición

${\displaystyle \begin{array}{l}\left({\left(\frac{d\Phi }{dx}\right)}_{L+}-{\left(\frac{d\Phi }{dx}\right)}_{L-}\right)+\frac{M}{T}{\omega }^2\Phi (L)=0\\ Ck-Ak\cos \left(kL\right)+\frac{M}{T}{\omega }^{2}D=0\end{array}}$

Expresamos esta ecuación

${\displaystyle \begin{array}{l}\frac{M}{Tk}{\omega }^2=\frac{M}{{\mu }_0}k=\frac{M}{m}kL\\ C-A\cos \left(kL\right)+\frac{M}{m}(kL)D=0\end{array}}$

• En x=2L se ha situado una masa puntual M, la función Φ(x) es continua en este punto

Csin(kL)+Dsin(kL)=F

• Por otra parte, la función Φ(x) ha de satisfacer la condición

${\displaystyle \begin{array}{l}\left({\left(\frac{d\Phi }{dx}\right)}_{2L+}-{\left(\frac{d\Phi }{dx}\right)}_{2L-}\right)+\frac{M}{T}{\omega }^2\Phi (2L)=0\\ E-C\cos \left(kL\right)+D\sin \left(kL\right)+\frac{M}{m}(kL)F=0\end{array}}$

Tenemos un sistema de cinco ecuaciones homogéneas con cinco incógnitas

${\displaystyle \begin{array}{l}\{\begin{array}{l}E\sin (kL)+F\cos (kL)=0\\ A\sin (kL)-D=0\\ -A\cos (kL)+C+\frac{M}{m}(kL)D=0\\ C\sin (kL)+D\cos (kL)-F=0\\ -C\cos (kL)+D\sin (kL)+E+\frac{M}{m}(kL)F=0\end{array}\\ \left(\begin{array}{ccccc}0& 0& 0& \sin (kL)& \cos (kL)\\ \sin (kL)& 0& -1& 0& 0\\ -\cos (kL)& 1& \frac{M}{m}(kL)& 0& 0\\ 0& \sin (kL)& \cos (kL)& 0& -1\\ 0& -\cos (kL)& \sin (kL)& 1& \frac{M}{m}(kL)\end{array}\right)\left(\begin{array}{c}A\\ C\\ D\\ E\\ F\end{array}\right)=0\end{array}}$

El determinante de la matriz de los coeficientes deberá ser cero

Llamamos x a kL y q al cociente M/m

>> syms q x;
>> M=[0,0,0,sin(x),cos(x); sin(x),0,-1,0,0;-cos(x),1,q*x,0,0;
0,sin(x),cos(x),0,-1;0,-cos(x),sin(x),1,q*x];
>> eq=det(M);
>> factor(eq)
ans =[ sin(x), 3*cos(x)^2 - sin(x)^2 + q^2*x^2*sin(x)^2 - 4*q*x*cos(x)*sin(x)]

La segunda expresión entre corchetes, se escribe, 4cos(x)² - 1 + q²x²sin(x)² - 4qxcos(x)sin(x). Comprobamos que es el producto de (qxsin(x)-2cos(x)+1)(qxsin(x)-2cos(x)-1).

>> eq=4*cos(x)^2 - 1 + q^2*x^2*sin(x)^2 - 4*q*x*cos(x)*sin(x);
>> factor(eq)
ans =[ q*x*sin(x) - 2*cos(x) + 1, q*x*sin(x) - 2*cos(x) - 1]

El determinante es el producto de tres factores

${\displaystyle \sin (kL)\left(\frac{M}{m}(kL)\sin (kL)-2\cos (kL)+1\right)\left(\frac{M}{m}(kL)\sin (kL)-2\cos (kL)-1\right)=0}$

Los valores de k_nL se obtienen de tres ecuaciones

• sin(kL)=0, cuya solución es

k_nL=nπ, n=1,2,3,...

• Las raíces k_nL de la ecuación transcendente

${\displaystyle \frac{M}{m}(kL)\sin (kL)-2\cos (kL)+1=0}$

• Las raíces k_nL de la ecuación transcendente

${\displaystyle \frac{M}{m}(kL)\sin (kL)-2\cos (kL)-1=0}$

Calculamos cuatro raíces k_nL de cada una de las tres ecuaciones. Las ordenamos mediante la función sort de MATLAB

L=1;
M_m=1; %cociente masas
%primera función
f=@(x) M_m*x.*sin(x)-2*cos(x)+1;
x=linspace(0,10,50);
r1=raices(f,x);
disp(r1);

%segunda función
g=@(x) M_m*x.*sin(x)-2*cos(x)-1;
x=linspace(0,10,50);
r2=raices(g,x);
disp(r2);

r3=(1:4)*pi/L;
disp(r3)

r=[r1,r2,r3];
sort(r)

    0.7314    3.8528    6.4356    9.7284
    1.3876    3.4159    6.7158    9.5288
    3.1416    6.2832    9.4248   12.5664
ans =    0.7314    1.3876    3.1416    3.4159    3.8528    6.2832    6.4356
    6.7158    9.4248    9.5288    9.7284   12.5664

Despejamos los coeficientes C, D, E y F del sistema de ecuaciones

${\displaystyle \{\begin{array}{l}D=A\sin (kL)\\ C=A\cos (kL)-\frac{M}{m}(kL)D\\ F=C\sin (kL)+D\cos (kL)\\ E=C\cos (kL)-D\sin (kL)-\frac{M}{m}(kL)F\end{array}}$

Cuando k_nL=nπ, sin(kL)=0, los coeficientes, D=0, C=Acos(kL), F=0 y E=Acos²(kL)=A

${\displaystyle \begin{array}{l}\Phi (x)=\{\begin{array}{l}A\sin (kx)0\le x<L\\ C\sin \left(k(x-L)\right)L\le x<2L\\ E\sin \left(k(x-2L)\right)2L\le x<3L\end{array}\\ \Phi (x)=\{\begin{array}{l}A\sin (kx)0\le x<L\\ A\cos (kL)\left(\sin (kx)\cos (kL)-\cos (kx)\sin (kL)\right)L\le x<2L\\ A\left(\sin (kx)\cos (2kL)-\cos (kx)\sin (2kL)\right)2L\le x<3L\end{array}\\ \Phi (x)=\{A\sin (kx)0\le x<3L\end{array}}$

Modos de vibración

${\displaystyle \Phi (x)=\{\begin{array}{l}A\sin (kx)0\le x<L\\ C\sin \left(k(x-L)\right)+D\cos \left(k(x-L)\right)L\le x<2L\\ E\sin \left(k(x-2L)\right)+F\cos \left(k(x-2L)\right)2L\le x<3L\end{array}}$

Los coeficientes C, D, E, F se expresan en términos de A

${\displaystyle \{\begin{array}{l}D=A\sin (kL)\\ C=A\cos (kL)-\frac{M}{m}(kL)D\\ F=C\sin (kL)+D\cos (kL)\\ E=C\cos (kL)-D\sin (kL)-\frac{M}{m}(kL)F\end{array}}$

Determinamos el valor del coeficiente A de modo que

${\displaystyle {\displaystyle \underset{0}{\overset{3L}{\int }}{\Phi }_n^2(x)·dx=1}}$

El resultado de calcular las integrales es

${\displaystyle \begin{array}{l}{A}^2{\displaystyle \underset{0}{\overset{L}{\int }}{\sin }^2(kx)dx}+{\displaystyle \underset{L}{\overset{2L}{\int }}{\left(C\sin \left(k(x-L)\right)+D\cos \left(k(x-L)\right)\right)}^{2}dx+{\displaystyle \underset{L}{\overset{2L}{\int }}{\left(E\sin \left(k(x-2L)\right)+F\cos \left(k(x-2L)\right)\right)}^{2}dx=1}}\\ A^2{\displaystyle \underset{0}{\overset{L}{\int }}{\sin }^2(kx)dx}+C^2{\displaystyle \underset{L}{\overset{2L}{\int }}{\sin }^2\left(k(x-L)\right)dx}+D^2{\displaystyle \underset{L}{\overset{2L}{\int }}{\cos }^2\left(k(x-L)\right)dx}+CD{\displaystyle \underset{L}{\overset{2L}{\int }}\sin \left(2k(x-L)\right)dx}+\\ +E^2{\displaystyle \underset{L}{\overset{2L}{\int }}{\sin }^2\left(k(x-2L)\right)dx}+F^2{\displaystyle \underset{L}{\overset{2L}{\int }}{\cos }^2\left(k(x-2L)\right)dx}+EF{\displaystyle \underset{L}{\overset{2L}{\int }}\sin \left(2k(x-L)\right)dx}=\\ \frac{1}{2}\left(A^2+C^2+D^2+E^2+F^2\right)+\frac{1}{4k}\sin \left(2kL\right)\left(-A^2-C^2+D^2-E^2+F^2\right)+\frac{1}{2k}\left(1-\cos \left(2kL\right)\right)(CD+EF)\end{array}}$

Representamos los tres primeros modos de vibración cuyos valores k₁=0.7314, k₂=1.3876, k₃=3.1416, hemos calculado

L=1; %longitud
M_m=1; %relación entre masas
A=1;

i=1;
for k=[0.7314, 1.3876, 3.1416]
    subplot(3,1,i)
    D=A*sin(k*L);
    C=A*cos(k*L)-M_m*(k*L)*D;
    F=C*sin(k*L)+D*cos(k*L);
    E=C*cos(k*L)-D*sin(k*L)-M_m*(k*L)*F;
    area=(A^2+C^2+D^2+E^2+F^2)/2+(-A^2-C^2+D^2-E^2+F^2)*sin(2*k*L)/(4*k)+
(C*D+E*F)*(1-cos(2*k*L))/(2*k);
    f1=@(x) sin(k*x)/sqrt(area);
    f2=@(x) (C*sin(k*(x-L))+D*cos(k*(x-L)))/sqrt(area);
    f3=@(x) (E*sin(k*(x-2*L))+ F*cos(k*(x-2*L)))/sqrt(area);
    hold on
    fplot(f1,[0,L])
    fplot(f2,[L,2*L])
    fplot(f3,[2*L,3*L])
    plot(L,f1(L),'ro','markersize',4,'markeredgecolor','r','markerfacecolor','r')
    plot(2*L,f2(2*L),'ro','markersize',4,'markeredgecolor','r','markerfacecolor','r')
    hold off
    grid on
    xlabel('x')
    ylabel('\Phi')
    title(sprintf('k=%1.2f',k))
    i=i+1;
end

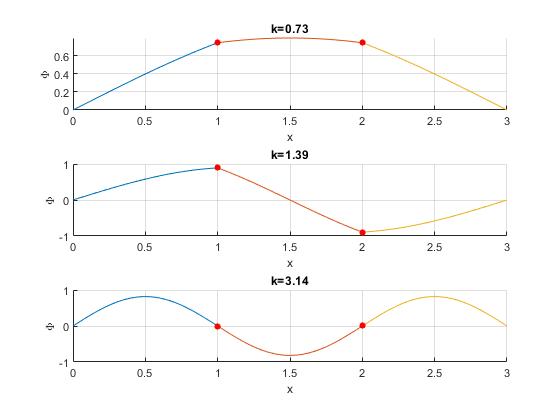
La tercera figura representa el tercer modo de vibración de una cuerda de longitud 3L. Para los modos múltiplos de tres, la función Φ(x) es continua y también su derivada. La partícula pernanece en reposo, no vibra, en un nodo. Para los otros modos, la función Φ(x) es continua pero no lo es su derivada, la partícula oscila.

Actividades

Se introduce

• El cociente de masas M/m (masa puntual dividido por la masa de una porción de la cuerda de longitud L) en el control titulado Masa M/m
• La longitud de la porción L de cuerda se ha fijado en L=1 m
• La velocidad de propagación de las ondas trasversales en la cuerda se ha fijado en v=1 m/s. El valor numérico del número de onda k coincide con el valor de la frecuencia angular ω, para calcular la frecuencia de los distintos modos de vibración f=ω/(2π)

Se pulsa el botón titulado Nuevo

Se pulsa el botón titulado >>, para observar el siguiente modo de vibración.

Se pulsa el botón titulado <<, para observar el modo de vibración anterior

En la parte superior, se muestra el modo de vibración y su frecuencia f en Hz.

Referencias

Gómez B. J. Repetto C. E., Stia C. R., Welti R. Oscillations of a string with concentrated masses. Eur. J. Phys. 28 (2007) pp. 961-975