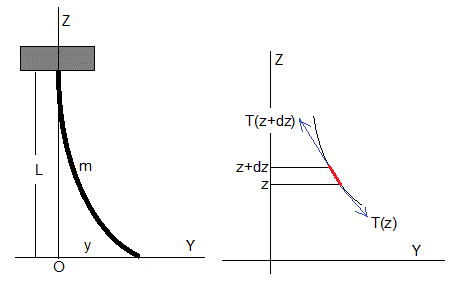
Sea una cadena suspendida verticalmente, de longitud L y masa m y densidad uniforme m/L. El origen y los ejes se muestran en la figura. El punto de suspensión tiene de coordenadas z=L, e y=0.

La deducción de la ecuación del movimiento de un elemento de la cuerda (señalado en color rojo en la figura de la derecha) es similar a la de las ondas transversales en una cuerda, la diferencia es que la tensión de la cuerda es constante y aquí la tensión de la cuerda en la posición z es el peso de la parte de la cuerda por debajo de z.

T(z)=(mz/L)g

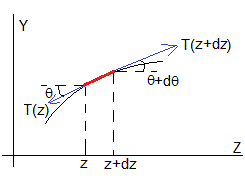
Consideremos una porción de cuerda comprendida entre z y z+dz

• T(z), es la fuerza que ejerce la parte de abajo de la cuerda sobre el elemento diferencial
• T(z+dz), es la fuerza que ejerce la parte de arriba de la cuerda sobre el elemento diferencial

Para deducir la ecuación del movimiento del elemento diferencial de la cuerda giramos los ejes, tal como se muestra en la figura

La componente Y de las fuerzas, dF_y, que actúan sobre dicho elemento diferencial de masa m·dz/L es

${\displaystyle \begin{array}{l}d{F}_y=T(z+dz)·\sin (\theta +d\theta )-T(z)\sin \theta \simeq \\ \left(T(z)+\frac{dT}{dz}dz\right)·(\sin \theta +\cos \theta ·d\theta )-T(z)\sin \theta =\\ \frac{d}{dz}\left(\sin \theta ·T(z)\right)·dz\simeq \frac{d}{dz}\left(\tan \theta ·T(z)\right)·dz=\frac{d}{dz}\left(\frac{dy}{dz}·T(z)\right)·dz\end{array}}$

Para ángulos pequeños, hacemos la aproximación sinθ≈tanθ

Esta componente dF_y de fuerza sobre el elemento diferencial de masa m·dz/L produce una aceleración a lo largo del eje Y. Teniendo en cuenta que y es una función de z y t, escribimos, la segunda ley de Newton, fuerza=masa×aceleración

${\displaystyle \begin{array}{l}\begin{array}{l}\frac{\partial }{\partial z}\left(\frac{\partial y}{\partial z}T(z)\right)dz=\left(\frac{m}{L}dz\right)\frac{{\partial }^{2}y}{\partial t^2}\\ \frac{\partial }{\partial z}\left(\frac{\partial y}{\partial z}\left(\frac{m}{L}gz\right)\right)=\left(\frac{m}{L}\right)\frac{{\partial }^{2}y}{\partial t^2}\end{array}\hfill \\ g\frac{\partial }{\partial z}\left(z\frac{\partial y}{\partial z}\right)=\frac{{\partial }^{2}y}{\partial t^2}\hfill \end{array}}$

Separación de variables

Escribimos la solución como producto, y(z,t)=X(z)·T(t), lo que nos permite sustituir una ecuación en derivadas particiales por dos ecuaciones diferenciales, una que depende de la variable z y otra de la variable t

${\displaystyle \begin{array}{l}g\frac{d}{dz}\left(z\frac{dX}{dz}\right)T=\frac{d^{2}T}{d{t}^2}X\\ \frac{\frac{d^{2}T}{d{t}^2}}{T}=\frac{g\frac{d}{dz}\left(z\frac{dX}{dz}\right)}{X}=-{\omega }^2\\ \{\begin{array}{l}\frac{d^{2}T}{d{t}^2}+{\omega }^{2}T=0\\ \frac{d}{dz}\left(z\frac{dX}{dz}\right)+\frac{{\omega }^2}{g}X=0\end{array}\end{array}}$

En la segunda ecuación diferencial, hacemos el cambio de variable

${\displaystyle \begin{array}{l}\begin{array}{l}x=2\sqrt{z}\hfill \\ \frac{dX}{dz}=\frac{dX}{dx}\frac{dx}{dz}=\frac{dX}{dx}\frac{2}{x}\hfill \end{array}\\ \frac{d}{dz}\left(z\frac{dX}{dz}\right)=\frac{d}{dz}\left(\frac{x^2}{4}\frac{dX}{dz}\right)=\frac{d}{dx}\left(\frac{x^2}{4}\frac{2}{x}\frac{dX}{dx}\right)\frac{dx}{dz}=\frac{d}{dx}\left(\frac{x}{2}\frac{dX}{dx}\right)\frac{2}{x}=\frac{1}{x}\frac{dX}{dx}+\frac{d^{2}X}{d{x}^2}\end{array}}$

Finalmente, llegamos a la ecución diferencial de Bessel con n=0

${\displaystyle x^2\frac{d^{2}X}{d{x}^2}+x\frac{dX}{dx}+\frac{{\omega }^2}{g}{x}^{2}X=0}$

La solución de la ecuación diferencial es

${\displaystyle X=A{J}_0\left(\sqrt{\frac{{\omega }^2}{g}}x\right)+B{Y}_0\left(\sqrt{\frac{{\omega }^2}{g}}x\right)}$

Ahora bien, la función Y₀(x) tiende a -∞ cuando x→0. La solución es

${\displaystyle X=A{J}_0\left(\sqrt{\frac{{\omega }^2}{g}}x\right)=A{J}_0\left(2\omega \sqrt{\frac{z}{g}}\right)}$

Dado que el punto de suspensión z=L, está fijo, X(L)=0, los posibles modos son las raíces ξ_n de la ecuación J₀(ξ)=0

${\displaystyle \begin{array}{l}2{\omega }_n\sqrt{\frac{L}{g}}={\xi }_n\\ {\omega }_n=\frac{1}{2}{\xi }_n\sqrt{\frac{g}{L}}\end{array}}$

Obtenemos las raíces de la ecuación transcendente utilizando la función, raices, que se ha definido en la página titulada Funciones MATLAB para calcular las raíces de una ecuación

L=1; %longitud
x=linspace(1,25,50);
disp('Frecuencias angulares')
w=raices(@(x) besselj(0,x),x)*sqrt(9.8/L)/2;
disp(w')

Las frecuencias angulares de vibración que corresponden a los sucesivos modos normales son

Frecuencias angulares
    3.7641
    8.6403
   13.5452
   18.4567
   23.3706
   28.2857
   33.2015
   38.1176

La solución de la ecuación diferencial dependiente del tiempo es conocida

${\displaystyle \begin{array}{l}\frac{d^{2}T}{d{t}^2}+{\omega }^2·T=0\hfill \\ T_n(t)=A_n\cos ({\omega }_{n}t)+B_n\sin ({\omega }_{n}t)\hfill \end{array}}$

donde A_n y B_n se determinan a partir de las condiciones iniciales. La solución de la ecuación diferencial correspondiente a la raíz n

${\displaystyle y_n(z,t)=X_n(x)T_n(t)=J_0\left({\xi }_n\sqrt{\frac{z}{L}}\right)\left\{A_n\cos \left(\frac{1}{2}{\xi }_n\sqrt{\frac{g}{L}}t\right)+B_n\sin \left(\frac{1}{2}{\xi }_n\sqrt{\frac{g}{L}}t\right)\right\}}$

Superposición

La solución completa es la superposición

${\displaystyle y(z,t)={\displaystyle \sum _{n=1}^{\infty }{y}_n(z,t)}={\displaystyle \sum _{n=1}^{\infty }{J}_0\left({\xi }_n\sqrt{\frac{z}{L}}\right)\left\{A_n\cos \left(\frac{1}{2}{\xi }_n\sqrt{\frac{g}{L}}t\right)+B_n\sin \left(\frac{1}{2}{\xi }_n\sqrt{\frac{g}{L}}t\right)\right\}}}$

Aplicamos las relaciones de ortogonalidad de las funciones de Bessel J₀(k_nx) para calcular los coeficientes A_n y B_n a partir de las condiciones iniciales en el instante t=0

${\displaystyle \begin{array}{l}\underset{0}{\overset{1}{{\displaystyle \int }}}z{J}_0(k_{m}z)J_0(k_{n}z)dz=0m\ne n\\ \underset{0}{\overset{1}{{\displaystyle \int }}}z{J}_0^2(k_{n}z)dz=\frac{1}{2}\left(J_0^2(k_n)+J_1^2(k_n)\right)=\frac{1}{2}{J}_1^2(k_n)\end{array}}$

J₀(k_n)=0, k_n son las raíces de la ecuación transcendente

Condiciones inicial y de contorno

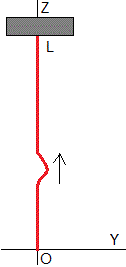
En la figura se muestra una cadena vertical de de masa m y longitud L, el extremo inferior z=0, está libre y el extremo superior z=L está sujeto al techo

El extremo x=L está fijo, y(L,t)=0, condición que ya hemos utilizado para calcular las frecuencias de los modos de vibración

La condición inicial es y(z,0)=0, la cadena en el instante t=0, tiene la dirección del eje Z .

Se golpea la cadena en la parte inferior de longitud αL, α<1, proporcionándole a ésta parte una velocidad V

${\displaystyle {\frac{\partial y(z,t)}{\partial t}|}_{t=0}=\{\begin{array}{l}V0\le z\le \alpha L\\ 0\alpha L<z\le L\end{array}}$

• La cadena tiene la dirección del eje Z en el instante t=0

${\displaystyle y(z\mathrm{,0})={\displaystyle \sum }_{n=1}^{\infty }{J}_0\left({\xi }_n\sqrt{\frac{z}{L}}\right)A_n=0}$

Esta condición implica que A_n=0

• Se proporciona una velocidad V a la parte inferior de la cadena de longitud αL

${\displaystyle \begin{array}{l}{\frac{\partial y(z,t)}{\partial t}|}_{t=0}={\displaystyle \sum _{n=1}^{\infty }{J}_0\left({\xi }_n\sqrt{\frac{z}{L}}\right)\frac{1}{2}{\xi }_n\sqrt{\frac{g}{L}}{B}_n}\\ {\displaystyle \underset{0}{\overset{1}{\int }}u\left({\frac{\partial y(z,t)}{\partial t}|}_{t=0}\right)J_0\left({\xi }_{n}u\right)du=}\frac{1}{2}{\xi }_n\sqrt{\frac{g}{L}}{B}_n{\displaystyle \underset{0}{\overset{1}{\int }}u{J}_0^2\left({\xi }_{n}u\right)du}\\ B_n=\sqrt{\frac{L}{g}}\frac{4{\displaystyle \underset{0}{\overset{1}{\int }}u·\left({\frac{\partial y(z,t)}{\partial t}|}_{t=0}\right)J_0\left({\xi }_{n}u\right)du}}{{\xi }_n·J_1^2\left({\xi }_n\right)}\\ B_n=V\sqrt{\frac{L}{g}}\frac{4{\displaystyle \underset{0}{\overset{\sqrt{\alpha }}{\int }}u·J_0\left({\xi }_{n}u\right)du}}{{\xi }_n·J_1^2\left({\xi }_n\right)}n=\mathrm{1,2,3...}\end{array}}$

Sustituyendo en el numerador la variable $u=\sqrt{\alpha }v$

${\displaystyle B_n=V\alpha \sqrt{\frac{L}{g}}\frac{4{\displaystyle \underset{0}{\overset{1}{\int }}v·J_0\left({\xi }_n\sqrt{\alpha }v\right)dv}}{{\xi }_n·J_1^2\left({\xi }_n\right)}=V\sqrt{\frac{L}{g}\alpha }\frac{4J_1\left({\xi }_n\sqrt{\alpha }\right)}{{\xi }_n^2·J_1^2\left({\xi }_n\right)}n=\mathrm{1,2,3...}}$

Para obtener esta última expresión, hemos utilizado la propiedad de las funciones de Bessel

${\displaystyle \underset{0}{\overset{1}{{\displaystyle \int }}}x{J}_0(kx)dx=\frac{1}{k}{J}_1(k)}$

La solución completa es

${\displaystyle y(z,t)={\displaystyle \sum _{n=1}^{\infty }{J}_0\left({\xi }_n\sqrt{\frac{z}{L}}\right)B_n\sin \left(\frac{1}{2}{\xi }_n\sqrt{\frac{g}{L}}t\right)}}$

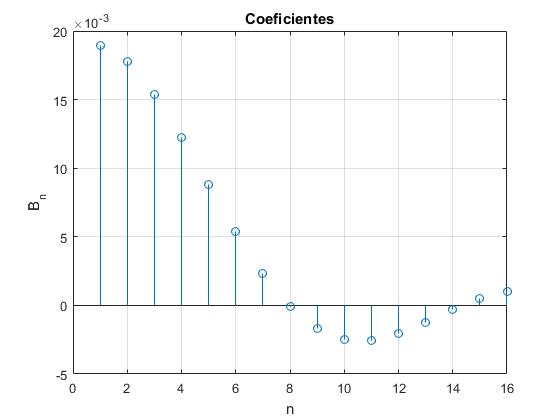
Coeficientes B_n

Creamos un script para calcular los ceficientes B_n, a partir de las raíces ξ_n de la ecuación J₀(ξ)=0. Se ha tomado un valor al parámetro α=0.025, se ha asignado al factor de escala

${\displaystyle 4V\sqrt{\frac{L}{g}}=1}$

alfa=0.025;
x=linspace(1,50,50);
xi=raices(@(x) besselj(0,x),x);
 
Bn=sqrt(alfa)*besselj(1,xi*sqrt(alfa))./(xi.*besselj(1,xi)).^2;
stem(Bn)
grid on
xlabel('n');
ylabel('B_n')
title('Coeficientes')

Oscilaciones del extremo inferior de la cadena

Creamos un script para representar gráficamente la desviación de la posición de equilibrio del extremos inferior z=0, en función del tiempo t. La cadena tiene una lomngitud L=0.12 m

El desarrollo en serie tiene infinitos términos, a efectos prácticos, se ha tomado la suma de los 63 primeros términos

Se representa y(z,τ), la desviación en función del tiempo adimensional

${\displaystyle \tau =\sqrt{\frac{g}{L}}t}$

L=0.12; %longitud
alfa=0.025;
x=linspace(1,200,100);
xi=raices(@(x) besselj(0,x),x);
Bn=sqrt(alfa)*besselj(1,xi*sqrt(alfa))./(xi.*besselj(1,xi)).^2;

z=0; %extremo libre de la cadena
i=1;
tt=0:0.01:20;
y=zeros(1,length(tt));
for t=tt
    for n=1:length(xi)
        y(i)=y(i)+besselj(0,xi(n)*sqrt(z/L))*Bn(n)*sin(xi(n)*t/2);
    end
    i=i+1;
end
plot(y,tt)
grid on
ylabel('\tau')
xlabel('y(z,t)')
title('Desplazamiento del extremo')

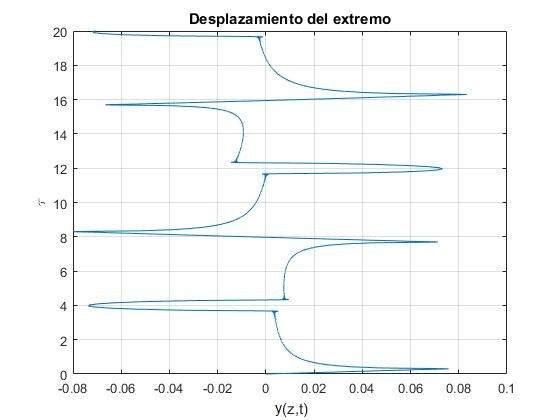
>> length(xi)
ans =    63

El tiempo de ida y vuelta de la perturbación, se puede estimar del siguiente modo. La velocidad de propagación de las ondas trasnversales en una cuerda de densidad μ y tensión T es $v=\sqrt{T/\mu }$, donde μ es la densidad lineal. Ahora bien, la tensión T=μgz de la cuerda no es constante. La velocidad dz/dt de propagación es

${\displaystyle \frac{dz}{dt}=\sqrt{\frac{\mu gz}{\mu }}=\sqrt{gz}}$

La solución de esta ecuación diferencial con la condición inicial t=0, z=0, es

${\displaystyle \begin{array}{l}2\sqrt{z}=\sqrt{g}t\\ z=\frac{1}{4}g{t}^2\end{array}}$

El tiempo que tarda en llegar el pulso al extremo superior z=L es

${\displaystyle t=2\sqrt{\frac{L}{g}}}$

El tiempo de ida y vuelta es el doble, o bien τ=4 unidades adimiensionales de tiempo, que es lo que aproximadamente, observamos en la gráfica

Actividades

Se introduce

• La porción del extremo inferior de la cadena αL golpeada, en el control titulado alfa. El valor que aparece en el control se divide entre 1000
• La velocidad que adquiere dicha porción en el instante t=0, en el control titulado Velocidad. El valor que aparece en el control se divide entre 10
• La longitud de la cadena se ha fijado en L=0.12 m

Se pulsa el botón titulado Nuevo

La cadena aparece colgada del techo, en la dirección del eje vertical Z. Un dispositivo golpea la parte inferior de la cadena de longitud αL, proporcionándole a dicha parte una velocidad V en el instante t=0

Observamos el desplazamiento horizontal de la cadena respecto d ela posición de equilibrio a medida que se propaga el pulso hacia arriba y hacia abajo

En la parte derecha, se representa el desplazamiento del extremo inferior z=0 (en el eje horizontal), en función del tiempo adimensional τ (en el eje vertical).

Referencias

Herb Bailey. Motion of a hanging chain after the free end is given an initial velocity. Am. J. Phys. 68(8) August 2000, pp. 764-767