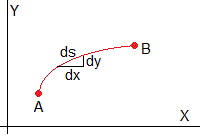
El índice de refracción n es el cociente entre la velocidad de la luz c en el vacío y la velocidad v de la luz en un medio material transparente. n=c/v

El tiempo que tarda la luz en recorrer el camino AB es

${\displaystyle {\displaystyle \underset{A}{\overset{B}{\int }}dt}={\displaystyle \underset{A}{\overset{B}{\int }}\frac{ds}{v}}=\frac{1}{c}{\displaystyle \underset{A}{\overset{B}{\int }}nds}}$

Esta última integral, se denomina camino óptico

En general el índice de refracción n no es constante sino que varía con x, con y o ambos, n=n(x, y). Para que el tiempo sea mínimo, tenemos que calcular el extremo de la funcional

${\displaystyle $ I={\displaystyle \underset{A}{\overset{B}{\int }}n(x,y)\sqrt{d{x}^2+d{y}^2}}={\displaystyle \underset{A}{\overset{B}{\int }}n(x,y)\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}dx}={\displaystyle \underset{A}{\overset{B}{\int }}n(x,y)\sqrt{1+{\dot{y}}^2}dx}$}$

La función f es

${\displaystyle f(x,y,\dot{y})=n(x,y)\sqrt{1+{\dot{y}}^2}}$

La ecuación de Euler-Lagrange se escribe

${\displaystyle \frac{\partial f}{\partial y}-\frac{d}{dx}\left(\frac{\partial f}{\partial \dot{y}}\right)=0}$

La ecuación diferencial del camino de la luz a través del medio es

${\displaystyle \begin{array}{l}\frac{\partial n}{\partial y}\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}-\frac{d}{dx}\left(n\frac{\left(\frac{dy}{dx}\right)}{\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}}\right)\\ \frac{\partial n}{\partial y}\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}-n\frac{\frac{d^{2}y}{d{x}^2}\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}-\frac{{\left(\frac{dy}{dx}\right)}^2}{\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}}\frac{d^{2}y}{d{x}^2}}{1+{\left(\frac{dy}{dx}\right)}^2}-\frac{\left(\frac{dy}{dx}\right)}{\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}}\frac{dn}{dx}=0\\ \frac{\partial n}{\partial y}\left(1+{\left(\frac{dy}{dx}\right)}^2\right)-n\frac{\frac{d^{2}y}{d{x}^2}}{1+{\left(\frac{dy}{dx}\right)}^2}-\left(\frac{dy}{dx}\right)\left(\frac{\partial n}{\partial x}+\frac{\partial n}{\partial y}\frac{dy}{dx}\right)=0\\ \frac{\frac{d^{2}y}{d{x}^2}}{1+{\left(\frac{dy}{dx}\right)}^2}-\frac{1}{n}\left(\frac{\partial n}{\partial y}-\frac{\partial n}{\partial x}\frac{dy}{dx}\right)=0\end{array}}$

Estudiaremos dos casos particulares:

El indice de refracción n varía con x

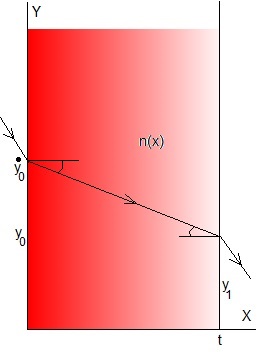
Supongamos una pieza de cierto material (un líquido contenido en un recipiente), de espesor t, que se ilumina con un rayo de luz a a la altura y₀. El rayo entra en la pieza x=0, formando un cierto ángulo tal que

${\displaystyle \tan {\theta }_0={\left(\frac{dy}{dx}\right)}_0={\dot{y}}_0}$

Cuando el índice de refracción n(x) varía horizontalmente, solamente depende de x, la ecuación diferencial del camino de la luz a través del medio es

${\displaystyle \begin{array}{l}\frac{\frac{d^{2}y}{d{x}^2}}{\left(1+{\left(\frac{dy}{dx}\right)}^2\right)\frac{dy}{dx}}=-\frac{1}{n}\frac{dn}{dx}\\ -{\displaystyle \underset{y_0}{\overset{y}{\int }}\frac{\frac{d^{2}y}{d{x}^2}}{\left(1+{\left(\frac{dy}{dx}\right)}^2\right)\frac{dy}{dx}}dx={\displaystyle \underset{n_0}{\overset{n}{\int }}\frac{dn}{n}}}\end{array}}$

Es una integral del tipo

${\displaystyle \begin{array}{l}-{\displaystyle \int \frac{dz}{z\left(1+z^2\right)}},z=\frac{dy}{dx}\\ -\frac{1}{z\left(1+z^2\right)}=\frac{A}{z}+\frac{Bz+C}{1+z^2},\{\begin{array}{l}A=-1\\ B=1\\ C=0\end{array}\\ {\displaystyle \int \left\{-\frac{1}{z}+\frac{z}{1+z^2}\right\}dz=}-\ln z+\frac{1}{2}\ln \left(1+z^2\right)=\frac{1}{2}\ln \left(1+\frac{1}{z^2}\right)\end{array}}$

El resultado es

${\displaystyle \begin{array}{l}\frac{1}{2}\ln \left(\frac{1+\frac{1}{{\left(\frac{dy}{dx}\right)}^2}}{1+\frac{1}{{\left(\frac{dy}{dx}\right)}_0^2}}\right)=\ln \left(\frac{n}{n_0}\right)\\ \frac{1+\frac{1}{{\dot{y}}^2}}{1+\frac{1}{{\dot{y}}_0^2}}=\frac{n^2(x)}{n_0^2}\end{array}}$

Integrando respecto de la variable x,obtenemos la desviación vertical Δy=y₁-y₀

${\displaystyle \begin{array}{l}\frac{1}{{\left(\frac{dy}{dx}\right)}^2}=\frac{n^2}{n_0^2}\left(1+\frac{1}{{\dot{y}}_0^2}\right)-1\\ \Delta y=y_1-y_0={\displaystyle \underset{0}{\overset{t}{\int }}\frac{dx}{\sqrt{\frac{n^2}{n_0^2}\left(1+\frac{1}{{\dot{y}}_0^2}\right)-1}}}\end{array}}$

El índice de refracción n varía con la altura y

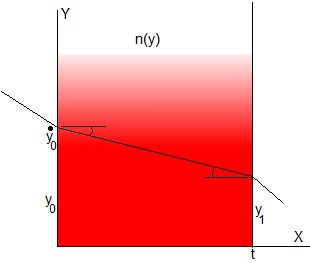
Cuando el índice de refracción n(y) varíaverticalmente, solamente depende de y, la ecuación diferencial del camino de la luz a través del medio es

${\displaystyle \frac{\frac{d^{2}y}{d{x}^2}}{\left(1+{\left(\frac{dy}{dx}\right)}^2\right)}=\frac{1}{n}\frac{dn}{dy}}$

Multiplicando por dy/dx

${\displaystyle \frac{\frac{d^{2}y}{d{x}^2}\frac{dy}{dx}dx}{\left(1+{\left(\frac{dy}{dx}\right)}^2\right)}=\frac{1}{n}\frac{dn}{dy}\frac{dy}{dx}dx}$

Tenemos una integral del tipo

${\displaystyle {\displaystyle \int \frac{z·dz}{1+z^2}}=\frac{1}{2}\ln \left(1+z^2\right),z=\frac{dy}{dx}}$

El resultado es

${\displaystyle \begin{array}{l}\frac{1}{2}\ln \left(\frac{1+{\left(\frac{dy}{dx}\right)}^2}{1+{\left(\frac{dy}{dx}\right)}_{y_0}^2}\right)={\displaystyle \underset{n(y_0)}{\overset{n}{\int }}\frac{dn}{n}}\\ \frac{1+{\left(\frac{dy}{dx}\right)}^2}{1+{\left(\frac{dy}{dx}\right)}_{y_0}^2}=\frac{n^2(y)}{n^2(y_0)}\end{array}}$

Integrando respecto de la variable x,obtenemos el espesor t del material

${\displaystyle \begin{array}{l}{\left(\frac{dy}{dx}\right)}^2=\frac{n^2}{n^2(y_0)}\left(1+{\left(\frac{dy}{dx}\right)}_{y_0}^2\right)-1\\ {\displaystyle \underset{0}{\overset{t}{\int }}dx}={\displaystyle \underset{y_0}{\overset{y_1}{\int }}\frac{dy}{\sqrt{\frac{n^2}{n^2(y_0)}\left(1+{\dot{y}}_0^2\right)-1}}},t={\displaystyle \underset{y_0}{\overset{y_1}{\int }}\frac{dy}{\sqrt{\frac{n^2}{n^2(y_0)}\left(1+{\dot{y}}_0^2\right)-1}}}\end{array}}$

En la página titulada Medida de la difusividad térmica, estudiamos un ejemplo interesante de este caso

El indice de refracción n varía con x.

Supongamos que el indice de refración varía con x, n=n(x). Como la función f

${\displaystyle f(x,y,\dot{y})=n(x)\sqrt{1+{\dot{y}}^2}}$

no depende de y. La ecuación de Euler-Lagrange se escribe

${\displaystyle \begin{array}{l}\frac{\partial f}{\partial y}-\frac{d}{dx}\left(\frac{\partial f}{\partial \dot{y}}\right)=0\\ \frac{d}{dx}\left(\frac{\partial f}{\partial \dot{y}}\right)=0\\ n(x)\frac{\dot{y}}{\sqrt{1+{\dot{y}}^2}}=C\\ \frac{dy}{dx}=\frac{\sqrt{C}}{\sqrt{n^2-C}}\end{array}}$

La constante C se determina sabiendo que para x=0

${\displaystyle \tan {\theta }_0={\left(\frac{dy}{dx}\right)}_0={\dot{y}}_0}$

Para una pieza de espesor t, obtenemos el mismo resultado que en el primer apartado

${\displaystyle \begin{array}{l}{\dot{y}}_0^2=\frac{C}{n_0^2-C},C=\frac{n_0^2{\dot{y}}_0^2}{1+{\dot{y}}_0^2}\\ {\left(\frac{dy}{dx}\right)}^2=\frac{\frac{n_0^2{\dot{y}}_0^2}{1+{\dot{y}}_0^2}}{n^2-\frac{n_0^2{\dot{y}}_0^2}{1+{\dot{y}}_0^2}}=\frac{n_0^2{\dot{y}}_0^2}{n^2\left(1+{\dot{y}}_0^2\right)-n_0^2{\dot{y}}_0^2}=\frac{1}{\frac{n^2}{n_0^2}\left(1+\frac{1}{{\dot{y}}_0^2}\right)-1}\\ \Delta y=y_1-y_0={\displaystyle \underset{0}{\overset{t}{\int }}\frac{dx}{\sqrt{\frac{n^2}{n_0^2}\left(1+\frac{1}{{\dot{y}}_0^2}\right)-1}}}\end{array}}$

Ejemplo. Ley de la refracción

Cuando el índice de refracción n es constante, la trayectoria y=y(x) es una línea recta

Consideremos el caso más sencillo: el índice de refracción n varía con x de la siguiente forma

${\displaystyle n(x)=\{\begin{array}{l}{n}_1{x}_1\le x\le x_m\\ n_2{x}_m\le x\le x_2\end{array}}$

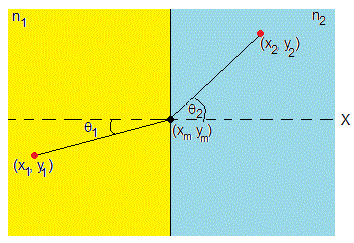
La ecuación de la recta que une el punto (x₁, y₁) con (x_m, y_m) es

${\displaystyle \tan {\theta }_1=\frac{y-y_1}{x-x_1}=\frac{\sqrt{C}}{\sqrt{n_1^2-C}}{x}_1\le x\le x_m}$

La ecuación de la recta que une el punto (x_m, y_m) con (x₂, y₂) es

${\displaystyle \tan {\theta }_2=\frac{y-y_m}{x-x_m}=\frac{\sqrt{C}}{\sqrt{n_2^2-C}}{x}_m\le x\le x_2}$

Relacionamos los ángulos θ₁ y θ₂

${\displaystyle \begin{array}{l}{\tan }^2{\theta }_1=\frac{C}{n_1^2-C}\\ {\tan }^2{\theta }_2=\frac{C}{n_2^2-C}\end{array}}$

En términos del sinθ

${\displaystyle \begin{array}{l}{\sin }^2{\theta }_1=\frac{C}{n_1^2}\\ {\sin }^2{\theta }_2=\frac{C}{n_2^2}\\ n_1\sin {\theta }_1=n_2\sin {\theta }_2\end{array}}$

que es la ley de Snell de la refracción

El índice de refracción n varía con la altura y

Consideremos ahora, un medio no homogéneo en el que el índice de refracción n varía con la altura y, n=n(y). Un ejemplo similar se estudia en la página titulada Espejismos

Como la función f

${\displaystyle f(x,y,\dot{y})=n(y)\sqrt{1+{\dot{y}}^2}}$

no depende de x. La ecuación de Euler-Lagrange se escribe

${\displaystyle \begin{array}{l}\frac{\partial f}{\partial x}-\frac{d}{dx}\left(f-\dot{y}\frac{\partial f}{\partial \dot{y}}\right)=0\\ f-\dot{y}\left(\frac{\partial f}{\partial \dot{y}}\right)=C_1\\ \frac{n(y)}{\sqrt{1+{\dot{y}}^2}}=C_1\end{array}}$

La constante C₁ se determina sabiendo que para x=0

${\displaystyle \tan {\theta }_0={\left(\frac{dy}{dx}\right)}_0={\dot{y}}_0}$

Para una pieza de espesor t, obtenemos el mismo resultado que en el primer apartado

${\displaystyle \begin{array}{l}\frac{n_0^2}{1+{\dot{y}}_0^2}=C_1^2\\ \frac{n^2}{1+{\left(\frac{dy}{dx}\right)}^2}=\frac{n_0^2}{1+{\dot{y}}_0^2}\\ {\left(\frac{dy}{dx}\right)}^2=\frac{n^2}{n_0^2}\left(1+{\dot{y}}_0^2\right)-1\\ {\displaystyle \underset{0}{\overset{t}{\int }}dx}={\displaystyle \underset{y_0}{\overset{y_1}{\int }}\frac{dy}{\sqrt{\frac{n^2}{n_0^2}\left(1+{\dot{y}}_0^2\right)-1}}},t={\displaystyle \underset{y_0}{\overset{y_1}{\int }}\frac{dy}{\sqrt{\frac{n^2}{n_0^2}\left(1+{\dot{y}}_0^2\right)-1}}}\end{array}}$

Ejemplo. El índice de rafracción se incrementa linealmente con la altura

Despejamos dy/dx e integramos

${\displaystyle \begin{array}{l}dx=C_1\frac{dy}{\sqrt{n^2(y)-C_1^2}}\\ x=C_1{\displaystyle \int \frac{dy}{\sqrt{n^2(y)-C_1^2}}}+C_2\end{array}}$

Como ejemplo, supongamos que el índice de refracción n se incrementa linealmente con la altura y, n(y)=n₀(1+αy)

${\displaystyle \begin{array}{l}x=C_1{\displaystyle \int \frac{dy}{\sqrt{n_0^2{(1+\alpha y)}^2-C_1^2}}}+C_2\\ x=\frac{C_1}{n_0\alpha }{\displaystyle \int \frac{dy}{\sqrt{{\left(\frac{1}{\alpha }+y\right)}^2-\frac{C_1^2}{n_0^2{\alpha }^2}}}}+C_2\end{array}}$

Como los parámetros n₀ y α son constantes, los incorporamos a la constante indeterminada C₁ para disponer de una expresión más simplificada

${\displaystyle x=C_1{\displaystyle \int \frac{dy}{\sqrt{{\left(\frac{1}{\alpha }+y\right)}^2-C_1^2}}}+C_2}$

Sea u=(1/α+y)/C₁, du=dy/C₁

${\displaystyle x=C_1{\displaystyle \int \frac{du}{\sqrt{u^2-1}}}+C_2}$

u=coshz, du=sinhz·dz

${\displaystyle \begin{array}{l}x=C_{1}z+C_2\\ x=C_1{\cosh }^{-1}\left(\frac{1}{C_1}\left(\frac{1}{\alpha }+y\right)\right)+C_2\\ \frac{1}{C_1}\left(\frac{1}{\alpha }+y\right)=\cosh \left(\frac{x-C_2}{C_1}\right)\\ y=-\frac{1}{\alpha }+C_1\cosh \left(\frac{x-C_2}{C_1}\right)\end{array}}$

Esta es la ecuación de la trayectoria. Calculamos las constantes C₁ y C₂ sabiendo que para x=0, y=y₀ y el rayo forma un ángulo θ con el eje X.

${\displaystyle y_0=-\frac{1}{\alpha }+C_1\cosh \left(\frac{C_2}{C_1}\right)}$

La pendiente dy/dx del rayo en x=0 es

${\displaystyle \tan \theta ={\left(\frac{dy}{dx}\right)}_{x=0}=-\sinh \left(\frac{C_2}{C_1}\right)}$

Teniendo en cuenta las relaciones

${\displaystyle \begin{array}{l}{\cosh }^{2}z-{\sinh }^{2}z=1\\ 1+{\tan }^2\theta =\frac{1}{{\cos }^2\theta }\end{array}}$

Despejamos C₁ y C₂

${\displaystyle \begin{array}{l}{C}_1=\left(y_0+\frac{1}{\alpha }\right)\cos \theta \\ C_2=-C_{{}_1}{\text{sinh}}^{-1}\left(\tan \theta \right)\end{array}}$

Posición del mínimo de la trayectoria

${\displaystyle \frac{dy}{dx}=\sinh \left(\frac{x-C_2}{C_1}\right)}$

La pendiente es cero para x_m=C₂

${\displaystyle y_m=-\frac{1}{\alpha }+C_1=-\frac{1}{\alpha }+\left(y_0+\frac{1}{\alpha }\right)\cos \theta }$

Un rayo que sale de y₀ con θ=0, tiene el mínimo x_m=0 e y_m=y₀, en el punto de partida.

Trazamos los rayos que salen del punto x=0, y₀=10, haciendo ángulos de -60, -30, 0, 30 y 60° con el eje X. Los rayos se propagan en un medio no homogéneo con índice de refracción que crece linealmente con la altura y, con α=2.3

alfa=2.3;
y0=10;
hold on
for th=(-60:30:60)*pi/180
    c1=(y0+1/alfa)*cos(th);
    c2=-c1*asinh(tan(th));
    f=@(x) -1/alfa+c1*cosh((x-c2)/c1);
    fplot(f,[0,10])
end
hold off
grid on
xlabel('x')
ylabel('y')
title('Trazado de rayos')

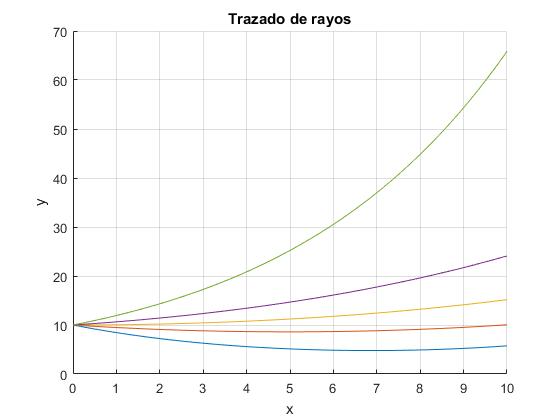
Comprobamos con la herramienta Data cursor de la ventana gráfica que el mínimo para la trayectoria cuyo ángulo θ=60°, es x_m=6.87, y_m=4.78

>> th=-pi/3;
>> c1=(y0+1/alfa)*cos(th);
>> c2=-c1*asinh(tan(th))
c2 =    6.8711
>>  ym=-1/alfa+(y0+1/alfa)*cos(th)
ym =    4.7826

Ecuación diferencial del camino de la luz a través del medio

En el primer apartado, obtuvimos esta ecuación diferencial para un medio de índice de refracción n(x,y)

${\displaystyle \frac{\frac{d^{2}y}{d{x}^2}}{1+{\left(\frac{dy}{dx}\right)}^2}-\frac{1}{n}\left(\frac{\partial n}{\partial y}-\frac{\partial n}{\partial x}\frac{dy}{dx}\right)=0}$

Para n(y)=n₀(1+αy) toma la forma

${\displaystyle \left(1+\alpha y\right)\frac{d^{2}y}{d{x}^2}=\left(1+{\left(\frac{dy}{dx}\right)}^2\right)\alpha }$

Integramos esta ecuación diferencial mediante el procedimiento numérico ode45, con las condiciones iniciales especificadas

alfa=2.3;
%rayo de luz
y0=10;
angulo=-60*pi/180;
f=@(t,x) [x(2);alfa*(1+x(2)^2)/(1+alfa*x(1))];
[t,x]=ode45(f,[0,10],[y0,tan(angulo)]); 
plot(t,x(:,1))
grid on
xlabel('x')
ylabel('y')
title('Indice n variable')

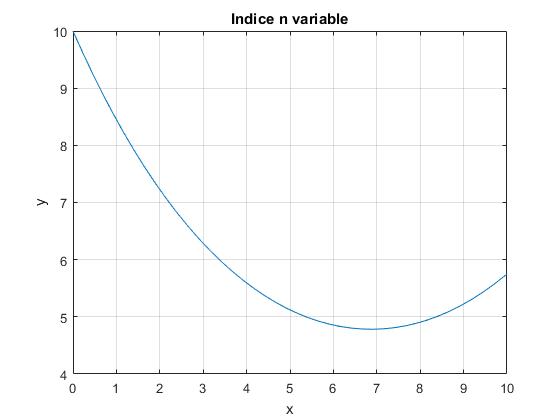
La solución numérica de la ecuación diferencial es útil en muchos casos que no es posible obtener una solución analítica, véase la página titulada Espejismos

Referencias

Javier E. Hasbun. On the optical path length in refracting media. Am. J. Phys. 86 (4) April 2018, pp. 268-274

J M H Peters. The deviation and curvature of light ray. Phys. Educ. 19 (1984) pp. 200-203