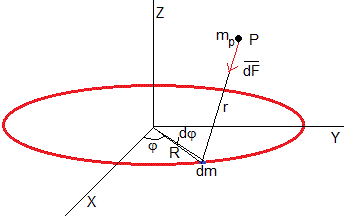
Consideremos un cuerpo de masa M en forma de anillo delgado de radio R. Representaremos las órbitas de una partícula de masa m_p en el plano YZ perpendicular al anillo y que pasa por su eje, tal como se muestra en la figura. Para ello, calculamreos las componentes F_y y F_z de la fuerza de atracción que ejerce el anillo sobre la partícula

Primero, calculamos la fuerza de atracción que ejerce un elemento dm de masa del anillo sobre la partícula

${\displaystyle \overrightarrow{dF}=-G\frac{m_p·dm}{r^3}\overrightarrow{r}}$

El vector $\overrightarrow{r}$ que une el elemento de masa dm, cuyas coordenadas son (Rcosφ, Rsinφ,0) con el punto P (0, y, z) situado en el plano YZ es

${\displaystyle \overrightarrow{r}=-R\cos \phi \widehat{i}+(y-R\sin \phi )\widehat{j}+z\widehat{k}}$

La fuerza de atracción es

${\displaystyle \overrightarrow{dF}=-G\frac{m_p·dm}{{\left(R^2+y^2+z^2-2yR\sin \phi \right)}^{3/2}}\left(-R\cos \phi \widehat{i}+(y-R\sin \phi )\widehat{j}+z\widehat{k}\right)}$

El elemento de masa dm

${\displaystyle dm=\frac{M}{2\pi R}Rd\phi =\frac{M}{2\pi }d\phi }$

Las componentes de dicha fuerza son

${\displaystyle \begin{array}{l}{F}_x=-G\frac{M{m}_p}{2\pi }{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{-R\cos \phi }{{\left(R^2+y^2+z^2-2yR\sin \phi \right)}^{3/2}}}d\phi \\ F_y=-G\frac{M{m}_p}{2\pi }{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{(y-R\sin \phi )}{{\left(R^2+y^2+z^2-2yR\sin \phi \right)}^{3/2}}}d\phi \\ F_z=-G\frac{M{m}_p}{2\pi }{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{z}{{\left(R^2+y^2+z^2-2yR\sin \phi \right)}^{3/2}}}d\phi \end{array}}$

Por simetría, la componente F_x se debería anular. Resolvemos la integral, haciendo el cambio u=R²+y²+z²-2yRsinφ, du=-2yRcosφ·dφ

${\displaystyle \begin{array}{l}{\displaystyle \int \frac{\cos \phi }{{\left(R^2+y^2+z^2-2yR\sin \phi \right)}^{3/2}}}d\phi =-\frac{1}{2yR}{\displaystyle \int \frac{du}{u^{3/2}}}=\frac{1}{yR}\frac{1}{\sqrt{R^2+y^2+z^2-2yR\sin \phi }}\\ {\frac{1}{\sqrt{R^2+y^2+z^2-2yR\sin \phi }}|}_0^{2\pi }=0\end{array}}$

Las ecuaciones del movimiento de la partícula son

${\displaystyle \begin{array}{l}{m}_p\frac{d^{2}y}{d{t}^2}=-G\frac{M{m}_p}{2\pi }{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{(y-R\sin \phi )}{{\left(R^2+y^2+z^2-2yR\sin \phi \right)}^{3/2}}}d\phi \\ m_p\frac{d^{2}z}{d{t}^2}=-G\frac{M{m}_p}{2\pi }{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{z}{{\left(R^2+y^2+z^2-2yR\sin \phi \right)}^{3/2}}}d\phi \end{array}}$

Escalas

Establecemos las siguientes escalas

${\displaystyle \tau =t\sqrt{\frac{GM}{R^3}},Y=\frac{y}{R},Z=\frac{z}{R}}$

El sistema de ecuaciones diferenciales se expresa en términos de la snuevas variables

${\displaystyle \begin{array}{l}\frac{d^{2}Y}{d{\tau }^2}=-\frac{1}{2\pi }{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{(Y-\sin \phi )}{{\left(1+Y^2+Z^2-2Y\sin \phi \right)}^{3/2}}}d\phi \\ \frac{d^{2}Z}{d{\tau }^2}=-\frac{1}{2\pi }{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{Z}{{\left(1+Y^2+Z^2-2Y\sin \phi \right)}^{3/2}}}d\phi \end{array}}$

Resolveremos el sistema de dos ecuaciones diferenciales utilizando procedimientos numéricos, con las siguientes condiciones iniciales: en el instante τ=0, Y=Y₀, (dY/dτ)₀=V_y0, Z=Z₀, (dZ/dτ)₀=V_z0

Energía

Cuando una partícula se mueve en un campo de fuerzas conservativo, la energía mecánica, permanece constante.

La energía cinética de la partícula es

${\displaystyle E_k=\frac{1}{2}{m}_p\left({\left(\frac{dY}{d\tau }\right)}^2+{\left(\frac{dZ}{d\tau }\right)}^2\right)}$

La energía potencial de la interacción entre el elemento diferencial de masa dm del anillo y la partícula es

${\displaystyle \begin{array}{l}d{E}_p=-G\frac{m_p·dm}{r}\\ d{E}_p=-G\frac{M}{2\pi }\frac{m_p·d\phi }{\sqrt{R^2+y^2+z^2-2yR\sin \phi }}\end{array}}$

Integramos para obtener la energía potencial de la interacción entre el anillo y la partícula

${\displaystyle E_p=-G\frac{M{m}_p}{2\pi }{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{d\phi }{\sqrt{R^2+y^2+z^2-2yR\sin \phi }}}}$

La suma de la energía cinética y potencial de la partícula se mantiene constante e igual a la energía en la situación inicial τ=0

${\displaystyle \frac{1}{2}{m}_p{v}^2-G\frac{M{m}_p}{2\pi }{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{d\phi }{\sqrt{R^2+y^2+z^2-2yR\sin \phi }}}=\text{cte}}$

Establecemos las escalas

${\displaystyle V=v\sqrt{\frac{R}{GM}},Y=\frac{y}{R},Z=\frac{z}{R}}$

La energía se expresa en términos de las nuevas variables

${\displaystyle E=\frac{1}{2}{V}^2-\frac{1}{2\pi }{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{d\phi }{\sqrt{1+Y^2+Z^2-2Y\sin \phi }}}}$

Trayectorias

Vamos a reproducir las trayectorias que aparecen en las figuras 2 y 5 del artículo que se menciona en la referencias, resolviendo el sistema de dos ecuaciones diferenciales con las condiciones iniciales que se especifican en la tabla

Calcularemos la energía inicial E₀ y final E de la partícula y el tanto por ciento de error

${\displaystyle \left|\frac{E-E_0}{E_0}\right|\times 100}$

Si el error fuera grande nos indicaría que el procedimiento numérico no ha realizado el cálculo de la trayectoria con la suficiente precisión.

Definimos las función anillo_gravitatorio que se pasa al procedimiento numérico ode45

function dr=anillo_gravitatorio(t, x)
    %Y es x(1) y Z es x(3)
   dr=zeros(4,1);
   dr(1)=x(2);
   f=@(phi) (x(1)-sin(phi))./(1+x(1)^2+x(3)^2-2*x(1)*sin(phi)).^(3/2);
   dr(2)=-integral(f,0,2*pi)/(2*pi);
   f=@(phi) x(3)./(1+x(1)^2+x(3)^2-2*x(1)*sin(phi)).^(3/2);
   dr(3)=x(4);
   dr(4)=-integral(f,0,2*pi)/(2*pi); 
end

Integramos el sistema de dos ecuaciones diferenciales y comprobamos la conservación de la energía para las siguientes condiciones iniciales, (segunda fila de la tabla): Y₀=0, (dY/dτ)₀=0.34, Z₀=0.5, (dZ/dτ)₀=0. Se representa la trayectoria hasta el tiempo (adimensional) τ_f=11.73

%x(1) es Y, x(2) es dY/dt, x(3) es Z, y x(4) dZ/dt
%x0=[0,0.422,0,0.422]; tf=9.465;
x0=[0,0.34,0.5,0]; tf=11.73;
%x0=[0.8,0,0,0.42]; tf=1.57;
%x0=[0,0.185,0.6,0]; tf=23.7;

%x0=[0,0.0836,1.95,0]; tf=32.805;
%x0=[0,0.159,0.35,0]; tf=26.75;
%x0=[0,0.985,0.5,0]; tf=52.2;
%x0=[0,0.4595,2,0]; tf=67.7;
%x0=[0,0.2076,0,1]; tf=29.6;
%x0=[0,0.2,2,0]; tf=84.3;
%x0=[1.2,0,0,0.4]; tf=4.57;

[t,x]=ode45(@anillo_gravitatorio,[0,tf],x0);
plot(x(:,1),x(:,3))
grid on
xlabel('x')
ylabel('y');
title('Orbita alrededor de un anillo')
%energía inicial
Y=x0(1);
Z=x0(3);
V2=x0(2)^2+x0(4)^2;
f=@(phi) 1./sqrt(1+Y^2+Z^2-2*Y*sin(phi));
E0=V2/2-integral(f,0,2*pi)/(2*pi);
%energía final
Y=x(end,1);
z=x(end,3);
V2=x(end,2)^2+x(end,4)^2;
E=V2/2-integral(f,0,2*pi)/(2*pi);
fprintf('Tanto por ciento de error, %2.3f\n', abs((E-E0)/E0)*100)

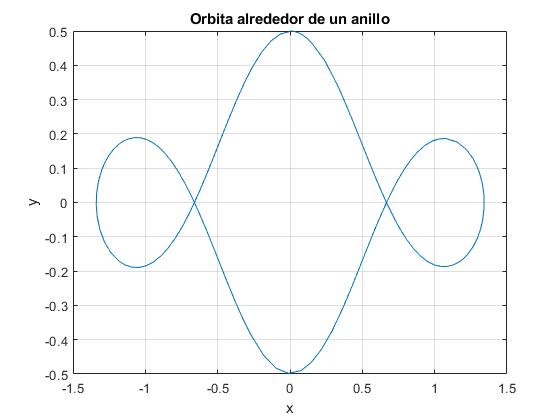
Al comprobar el principio de conservación de la energía, vemos que el error es pequeño

Tanto por ciento de error, 0.116

Sean ahora las condiciones iniciales, (fila 7 de la tabla): Y₀=0, (dY/dτ)₀=0.985, Z₀=0.5, (dZ/dτ)₀=0. Se representa la trayectoria hasta el tiempo (adimensional) τ_f=52.2

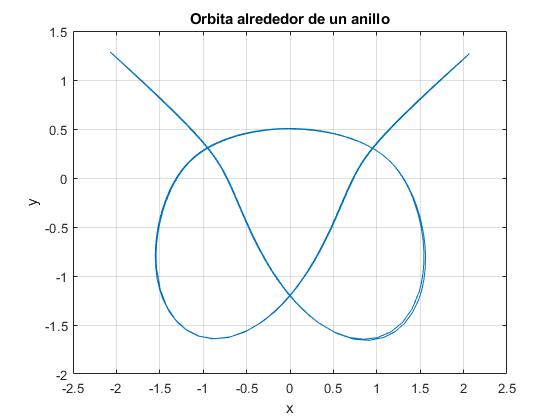
Tanto por ciento de error, 4.105

Sean ahora las condiciones iniciales, (fila 10 de la tabla): Y₀=0, (dY/dτ)₀=0.2, Z₀=2, (dZ/dτ)₀=0. Se representa la trayectoria hasta el tiempo (adimensional) τ_f=84.3

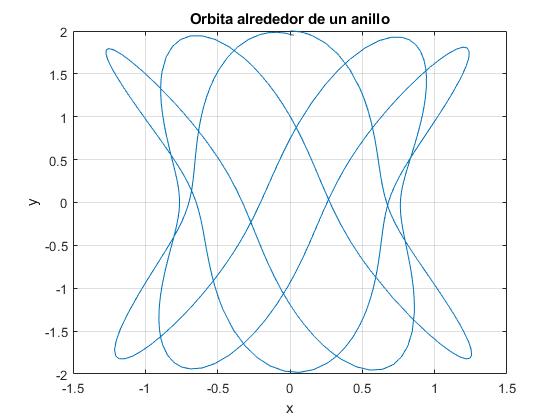
Tanto por ciento de error, 1.584

Hay trayectorias que dan un error elevado, por ejemplo, la que corresponde a la última fila de la tabla

Referencias

R Wesley Tobin, J West Closed orbits about a massive thin ring. Eur. J. Phys. 27 (2006) pp. 215-223