Consideremos ahora que una partícula de masa m se mueve bajo la acción de una combinación de dos fuerzas centrales:

• Una atractiva, proporcional al cuadrado de las distancia r de la la partícula al centro de fuerzas que estudiamos en la página Ecuación de la trayectoria
• Una fuerza atractiva o repulsiva, proporcional al cubo de las distancia r, que hemos estudiado en la sección anterior y que denominaremos perturbación

Para deducir la ecuación de la trayectoria, seguiremos los mismos pasos que en la página titulada 'Movimiento bajo una fuerza inversamente proporcional al cubo de la distancia'

Si la energía potencial de la partícula es

${\displaystyle E_p(r)=-\frac{k}{r}-\frac{\alpha }{r^2}}$

La fuerza central es

${\displaystyle \begin{array}{l}F(r)=-\frac{d}{dr}{E}_p(r)\\ F(r)=-\frac{k}{r^2}-\frac{2\alpha }{r^3}\end{array}}$

Las ecuaciones del movimiento en coordendas polares

${\displaystyle \begin{array}{l}m\left(\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2\right)=-\frac{k}{r^2}-\frac{2\alpha }{r^3}\hfill \\ m\left(r\frac{d^2\theta }{d{t}^2}+2\frac{d\theta }{dt}\frac{dr}{dt}\right)=0\hfill \end{array}}$

Teniendo en cuenta la constancia del momento angular L, escribimos la ecuación del movimiento en la dirección radial de la forma

${\displaystyle \frac{d^{2}r}{d{t}^2}+\frac{1}{r^3}\left(\frac{2\alpha }{m}-\frac{L^2}{m^2}\right)+\frac{k}{m}\frac{1}{r^2}=0}$

Seguidamente, obtenemos una ecuación en términos de r y de sus derivadas respecto del ángulo θ

${\displaystyle \frac{d^{2}r}{d{\theta }^2}-\frac{2}{r}{\left(\frac{dr}{d\theta }\right)}^2+r\left(\frac{2m\alpha }{L^2}-1\right)+\frac{mk}{L^2}{r}^2=0}$

Hacemos el cambio de variable u=1/r. La ecuación del movimiento se convierte en

${\displaystyle \frac{d^{2}u}{d{\theta }^2}+\left(1-\frac{2\alpha m}{L^2}\right)u=\frac{mk}{L^2}}$

Llamamos

${\displaystyle {\beta }^2=\frac{L^2-2\alpha m}{L^2}1-\frac{2\alpha m}{L^2}>0}$

La solución particular es u=C, introduciéndolo en la ecuación diferencial

${\displaystyle C=\frac{mk}{L^2-2\alpha m}=\frac{mk}{{\beta }^2{L}^2}}$

La solución completa de la ecuación diferencial en u es

${\displaystyle u=A\sin (\beta \theta )+B\cos (\beta \theta )+\frac{mk}{{\beta }^2{L}^2}}$

De forma alternativa

${\displaystyle \begin{array}{l}A\frac{{\beta }^2{L}^2}{mk}=\epsilon \sin \beta {\theta }_{0}B\frac{{\beta }^2{L}^2}{mk}=\epsilon \cos \beta {\theta }_0\\ u=\frac{mk}{{\beta }^2{L}^2}\left(\epsilon \cos \beta (\theta -{\theta }_0)+1\right)\end{array}}$

Calculamos la constante ε a partir de la constancia de la energía

${\displaystyle \begin{array}{l}E=\frac{1}{2}m\left\{{\left(\frac{dr}{dt}\right)}^2+r^2{\left(\frac{d\theta }{dt}\right)}^2\right\}-\frac{k}{r}-\frac{\alpha }{r^2}\\ E=\frac{1}{2}\frac{L^2}{m{r}^4}\left\{{\left(\frac{dr}{d\theta }\right)}^2+r^2\right\}-\frac{k}{r}-\frac{\alpha }{r^2}\\ E=\frac{1}{2}\frac{L^2}{m}{u}^4\left\{\frac{1}{u^4}{\left(\frac{du}{d\theta }\right)}^2+\frac{1}{u^2}\right\}-ku-\alpha u^2\\ E=\frac{1}{2}\left\{\frac{L^2}{m}{\left(\frac{du}{d\theta }\right)}^2+\left(\frac{L^2}{m}-2\alpha \right)u^2\right\}-ku\\ E=\frac{1}{2}\left\{\frac{L^2}{m}{\left(\frac{du}{d\theta }\right)}^2+\frac{{\omega }^2{L}^2}{m}{u}^2\right\}-ku\end{array}}$

Introduciendo la expresión de u y su derivada du/dθ, obtenemos

${\displaystyle \epsilon =\sqrt{1+\frac{2{\beta }^2{L}^2}{m{k}^2}E}}$

La ecuación de la trayectoria es r=1/u

${\displaystyle r=\frac{r_0}{1+\epsilon \cos \beta (\theta -{\theta }_0)}{r}_0=\frac{{\beta }^2{L}^2}{mk}}$

Cuando β se expresa como un número racional β=m/n, el numerador m indica la simetría y el denominador n el número de vueltas que el radio vector da alrededor del origen. La órbita es cerrada siempre que β sea un número racional.

β es un número racional

beta=4/5;
e=4/5;
th=0:pi/72:10*pi;
r=1./(1+e*cos(beta*th));
plot(r.*cos(th),r.*sin(th))
grid on
axis equal
xlabel('x')
ylabel('y')
title('\beta=4/5,\epsilon=4/5')

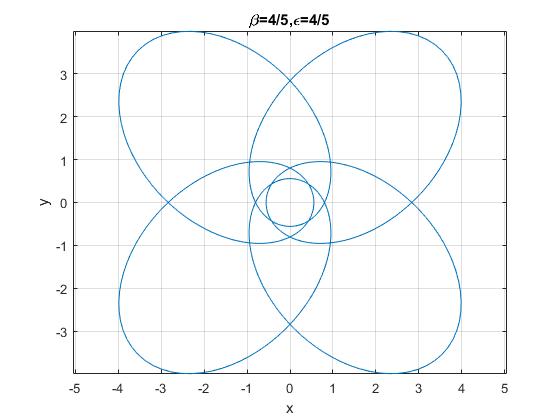
Como casos curiosos, las trayectorias de la forma β=1/n

beta=1/3;
e=4/5;
th=0:pi/72:6*pi;
r=1./(1+e*cos(beta*th));
plot(r.*cos(th),r.*sin(th))
grid on
axis equal
xlabel('x')
ylabel('y')
title('\beta=1/3,\epsilon=4/5')

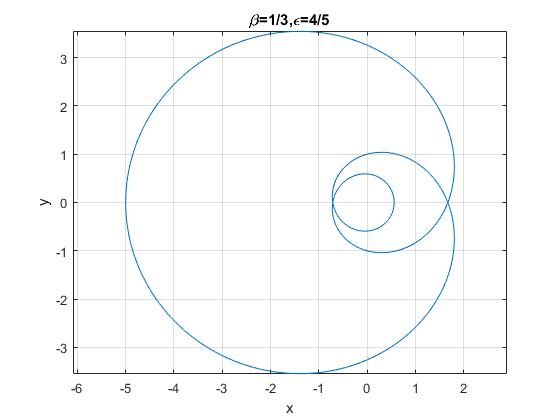
o las trayectorias de la forma β=n

beta=3;
e=4/5;
th=0:pi/72:2*pi;
r=1./(1+e*cos(beta*th));
plot(r.*cos(th),r.*sin(th))
grid on
axis equal
xlabel('x')
ylabel('y')
title('\beta=3,\epsilon=4/5')

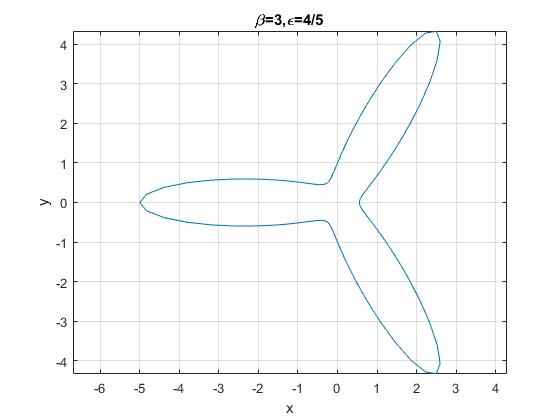
β no es un número racional

beta=(2+pi)/(2*pi);
e=4/5;
th=0:pi/72:11*pi;
r=1./(1+e*cos(beta*th));
plot(r.*cos(th),r.*sin(th))
grid on
axis equal
xlabel('x')
ylabel('y')
title('\beta=(2+\pi)/(2\pi),\epsilon=4/5')

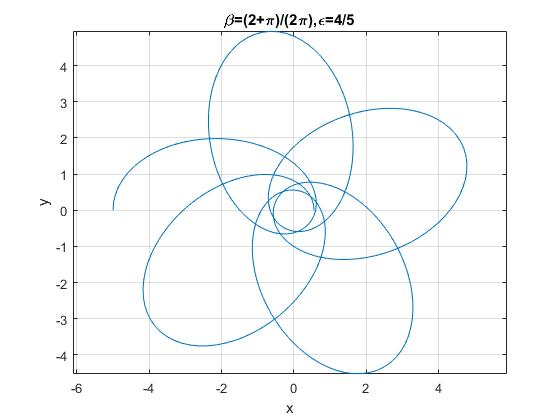
La trayectoria no es cerrada

Periodos

Denominaremos periodo radial P_r al tiempo que tarda el móvil en dar dos pasos consecutivos por el perihelio o por el afelio, y el periodo orbital P_θ al tiempo necesario para que el móvil dé una vuelta completa al origen. La relación entre ambos periodos cuando β=m/n (número racional) es la siguiente

m·P_r=n·P_θ

La energía de la partícula en coordenadas polares es

${\displaystyle \begin{array}{l}E=\frac{1}{2}m\left\{{\left(\frac{dr}{dt}\right)}^2+r^2{\left(\frac{d\theta }{dt}\right)}^2\right\}+E_p(r)\\ E=\frac{1}{2}m\left\{{\left(\frac{dr}{dt}\right)}^2+r^2\frac{L^2}{m^2{r}^4}\right\}+E_p(r)\\ E=\frac{1}{2}m{\left(\frac{dr}{dt}\right)}^2+\frac{L^2}{2m{r}^2}+E_p(r)\end{array}}$

Los dos últimos términos, se denominan energía potencial efectiva

Para analizar cualitativamente, el movimiento en la direción radial, se representa la energía potencial efectiva en función de la distancia radial r. Se traza una recta horizontal que representa la energía total E. Los puntos de intersección corresponden a las distancias máxima r₂ y mínima r₁ al centro de fuerzas

hold on
fplot(@(x) 1./x.^2-1./x, [1,10],'color','k') %energía potencial efectiva
x1=(1-sqrt(0.2))/0.4;
x2=(1+sqrt(0.2))/0.4;
line([0,10],[-0.2,-0.2],'color','r') %energía 
line([x1,x1],[-0.2,0],'lineStyle','--') %distancia mínima
line([x2,x2],[-0.2,0],'lineStyle','--') %distancia máxima
hold off
grid on
xlabel('r')
ylabel('V_e(r)')
title('Energía potencial efectiva')

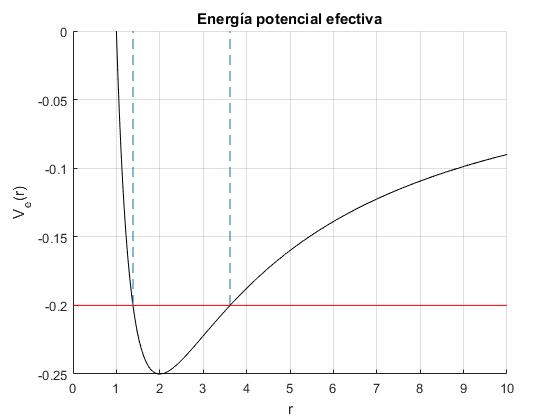
Se denomina periodo del movimiento radial P_r al doble del tiempo que tarda la partícula en desplazarse desde r₁ a r₂

${\displaystyle \begin{array}{l}\frac{dr}{dt}=\sqrt{\frac{2}{m}\left(E-\frac{L^2}{2m{r}^2}-E_p(r)\right)}\\ P_r={\displaystyle \underset{r_1}{\overset{r_2}{\int }}\sqrt{\frac{2m}{E-\frac{L^2}{2m{r}^2}-E_p(r)}}dr}\end{array}}$

De la constancia del momento angular deducimos la fórmula del periodo del movimiento angular, P_θ.

${\displaystyle \begin{array}{l}L=m{r}^2\frac{d\theta }{dt}\\ P_{\theta }=\frac{m}{L}{\displaystyle \underset{0}{\overset{2\pi }{\int }}{r}^{2}d\theta }\end{array}}$

Calculamos los periodos P_r y P_θ para el potencial E_p(r)=-k/r-α/r²

Periodo del movimiento radial

${\displaystyle P_r={\displaystyle \underset{r_1}{\overset{r_2}{\int }}\sqrt{\frac{2m}{E-\frac{{\beta }^2{L}^2}{2m{r}^2}+\frac{k}{r}}}dr}=2m{\displaystyle \underset{r_1}{\overset{r_2}{\int }}\frac{rdr}{\sqrt{2mE{r}^2+2mkr-{\beta }^2{L}^2}}}}$

donde r₁ y r₂ son las raíces de la ecuación

${\displaystyle \begin{array}{l}2mE{r}^2+2mkr-{\beta }^2{L}^2=\mathrm{0,}E<0\\ r_1=\frac{-mk+\sqrt{m^2{k}^2+2mE{\beta }^2{L}^2}}{2mE}\\ r_2=\frac{-mk-\sqrt{m^2{k}^2+2mE{\beta }^2{L}^2}}{2mE}\end{array}}$

Como E<0, ambas raíces son positivas

Calculamos la integral, véase la página titulada Trayectorias elípticas (II)

${\displaystyle {\displaystyle \int \frac{x·dx}{\sqrt{-a{x}^2+bx-c}}}=-\frac{1}{a}\sqrt{-a{x}^2+bx-c}+\frac{b}{2a^{3/2}}\arcsin \left(\frac{2ax-b}{\sqrt{b^2-4ac}}\right)}$

Finalmente, el periodo P_r es

${\displaystyle \begin{array}{l}{P}_r=2m{\left\{\begin{array}{l}-\frac{1}{-2mE}\sqrt{2mE{r}^2+2mkr-{\beta }^2{L}^2}+\\ \frac{mk}{{\left(-2mE\right)}^{3/2}}\arcsin \left(\frac{-2mEr-mk}{\sqrt{m^2{k}^2+2mE{\beta }^2{L}^2}}\right)\end{array}\right\}}_{r_1}^{r_2}=\\ \frac{2m^{2}k}{{\left(-2mE\right)}^{3/2}}\left\{\arcsin (1)-\arcsin (-1)\right\}=\pi k\sqrt{\frac{-m}{2E^3}}\end{array}}$

Como el periodo radial es independiente del momento angular, por tanto, no lo modifica la perturbación

Periodo del movimiento angular

Para entender el periodo del movimiento angular consideremos el caso de que β=p/q sea un número racional, por ejemplo β=1/3.

beta=1/3;
e=4/5;
hold on
for i=1:3
    th=(i-1)*2*pi:pi/72:i*2*pi;
    r=1./(1+e*cos(beta*th));
    plot(r.*cos(th),r.*sin(th))
end
hold off
grid on
axis equal
xlabel('x')
ylabel('y')
title('\beta=1/3,\epsilon=4/5')

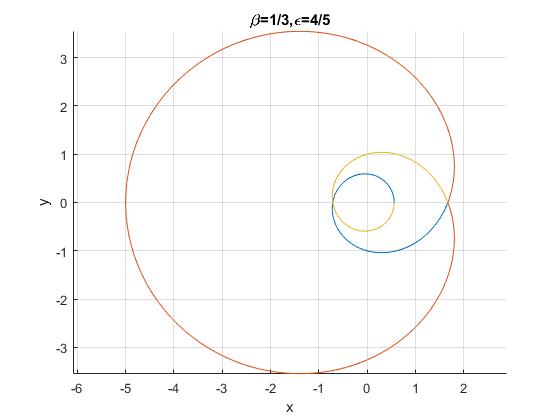
La trayectoria es la suma de q (tres) intervalos angulares (cada intervalo en un color diferente), de 0≤θ<2π, 2π≤θ<4π y 4π≤θ<6π. El tiempo que invierte la partícula en desplazarse en cada intervalo angular no es el mismo. El tiempo total es P_θ

${\displaystyle P_{\theta }=\frac{m}{L}{\displaystyle \underset{0}{\overset{2\pi q}{\int }}{r}^{2}d\theta }=\frac{m}{L}{\left(\frac{{\beta }^2{L}^2}{mk}\right)}^2{\displaystyle \underset{0}{\overset{2\pi q}{\int }}\frac{1}{{\left(1+\epsilon \cos \beta \theta \right)}^2}d\theta }}$

hacemos el cambio de variable, φ=βθ, dφ=β·dθ

${\displaystyle P_{\theta }=\frac{{\beta }^3{L}^3}{m{k}^2}{\displaystyle \underset{0}{\overset{2\pi \beta q}{\int }}\frac{d\phi }{{\left(1+\epsilon \cos \phi \right)}^2}}=\frac{{\beta }^3{L}^3}{m{k}^2}{\displaystyle \underset{0}{\overset{2\pi p}{\int }}\frac{d\phi }{{\left(1+\epsilon \cos \phi \right)}^2}}=p\frac{{\beta }^3{L}^3}{m{k}^2}{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{d\phi }{{\left(1+\epsilon \cos \phi \right)}^2}}}$

Teniendo en cuenta el valor de la integral, véase la página titulada Trayectorias elípticas (II)

${\displaystyle \begin{array}{l}{\displaystyle \int \frac{d\phi }{{\left(1+\epsilon \cos \phi \right)}^2}}=\frac{1}{{\left(1-{\epsilon }^2\right)}^{3/2}}\left\{2{\tan }^{-1}\left(\sqrt{\frac{1-\epsilon }{1+\epsilon }}\tan \frac{\phi }{2}\right)-\epsilon \sqrt{1-{\epsilon }^2}\frac{\sin \phi }{1+\epsilon \cos \phi }\right\}\\ {\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{d\phi }{{\left(1+\epsilon \cos \phi \right)}^2}}=2{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{d\phi }{{\left(1+\epsilon \cos \phi \right)}^2}}=\frac{2\pi }{{\left(1-{\epsilon }^2\right)}^{3/2}}\end{array}}$

La relación entre los dos periodos es

${\displaystyle P_{\theta }=p\frac{{\beta }^3{L}^3}{m{k}^2}\frac{2\pi }{{\left(1-{\epsilon }^2\right)}^{3/2}}=p{P}_r}$

Precesión de las órbitas

Otro concepto interesante, es la velocidad de precesión Ω del afelio (perihelio), que se define como el cociente entre la distancia angular Δθ entre dos pasos consecutivos por el afelio (perihelio) y el tiempo que tarda o periodo radial P_r. La distancia angular es el intervalo para el cual βθ se incrementa en 2π es decir, Δθ=2π/β. La velocidad de precesión es

${\displaystyle \Omega =\frac{\Delta \theta }{P_r}=\frac{2\pi }{\beta P_r}}$

Actividades

Se introduce

• El parámetro β, en el control titulado β
• La posición inicial x, la ordenada y=0, en el control titulado Posición X
• La componente Y de la velocidad inicial v_y, la componente X de la velocidad v_x=0, en el control titulado Velocidad V_y
• Se ha fijado el valor de k=1
• Se ha fijado la masa de la partícula, m=1

Se pulsa el botón titulado Nuevo y a continuación ►, se traza la trayectoria de la partícula, se muestra como van cambiando los valores de la posición (X, Y) y su distancia r al centro de fuerzas, y las componentes (V_x, V_y) de la velocidad y su módulo v a medida que transcurre el tiempo t.

Observaremos que la energía y el momento angular permanecen constantes. En la parte inferior izquierda, se muestra en color rojo el tanto por ciento de error. Cuando es mayor que la unidad el programa interactivo se detiene. Los mayores porcentajes de error se obtienen cuando la partícula pasa muy cerca del centro fijo de fuerzas.

Se pulsa el botón titulado pausa || y luego, paso a paso >|, para acercarnos a una posición determinada con el fin de medir los periodos P_r y P_θ.

Ejemplo

• Sea β=p/q=1/3. Posición inicial x₀=2, velocidad inicial V_0y=1

El parámetro α vale

${\displaystyle \begin{array}{l}{\beta }^2=\frac{L^2-2\alpha m}{L^2}1-\frac{2\alpha m}{L^2}>0\\ \alpha =\frac{L^2\left(1-{\beta }^2\right)}{2m}\end{array}}$

La energía y el momento angular valen

${\displaystyle \begin{array}{l}E=\frac{1}{2}{v}_{0y}^2-\frac{1}{x_0}-\frac{\alpha }{x_0^2}\\ L=x_0{v}_{0y}\end{array}}$

Donde $\overrightarrow{r}=x_0\widehat{i},\overrightarrow{v}=v_{0y}\widehat{j}$ es la posicón inicial y velocidad inicial, respectivamente.

Detenemos el movimiento cuando la posición angular es θ=2π, 4π, 6π (cuando pasa por el eje X positivo, y=0). Medimos los tiempos, 3.63, 3.86, 7.48. El tiempo total en dar q=3 (denominador) vueltas completas es 7.48

La distancia desde la partícula al centro de fuerzas es r=2 en el instante t=0 y vuelve a ser r=2 en el instante 7.48 s

Se cumple que P_θ=p·P_r, donde p (numerador) es 1

• Sea β=p/q=2/3. Posición inicial x₀=2, velocidad inicial V_0y=1

Detenemos el movimiento cuando la posición angular es θ=2π, 4π, 6π (cuando pasa por el eje X positivo, y=0). Medimos los tiempos, 9.67, 20.68, 30.34 . El tiempo total en dar q=3 (denominador) vueltas completas es 30.34

La distancia desde la partícula al centro de fuerzas es r=2 (posición x=2, y=0) en el instante t=0 y vuelve a ser r=2 (posición x=-2, y=0) en el instante 15.17 s

Se cumple que P_θ=p·P_r, donde p (numerador) es 2

Referencias

O.L. de Lange, J. Pierrus. Solved Problems in Classical Mechanics. Analytical and numerical solutions with comments. Oxford University Press (2010). Questions 8.12, 8.16