Transferencia mediante dos órbitas elípticas

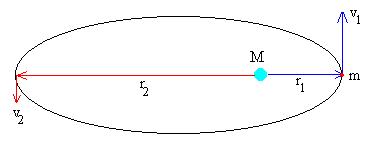
Recordaremos que en una órbita elíptica, dadas las distancias al prerigeo, r₁ y al apogeo, r₂ calculamos las velocidades máxima y mínima en en dichas posiciones v₁ y v₂, aplicando la constancia del momento angular y de la energía (fuerza central y conservativa)

$v_{2} = \sqrt{\frac{2 G M r_{1}}{r_{2} (r_{1} + r_{2})}}, v_{1} = \sqrt{\frac{2 G M r_{2}}{r_{1} (r_{1} + r_{2})}}$

Examinamos la transferencia entre dos órbitas circulares de radios r_A y r_B mediante dos órbitas elípticas. La primera parte de la órbita circular interior A hasta una posición C alejada, la segunda parte de C hasta la órbita circular exterior B. La idea es poner C suficientemente alejado del foco, de esta forma este tipo de transferencia es más eficiente (consume menos combustible) que la de Hohmann, como veremos al final de esta página.

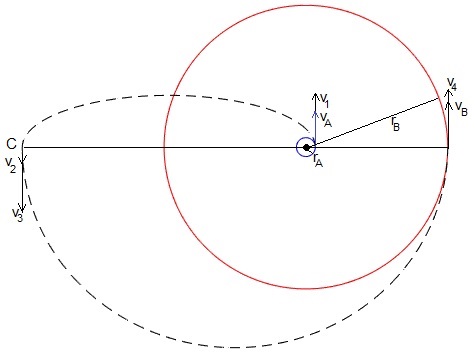
Veamos un ejemplo

Radio de la órbita circular interior r_A=7 000 km
Radio de la órbita circular exterior r_B=105 000 km
Posición C, r_C=210 000 km

Las etapas del movimiento de la nave espacial son

Orbita circular interior de radio r_A

La velocidad de la nave espacial en la órbita circular es

$m \frac{v_{A}^{2}}{r_{A}} = \frac{G M m}{r_{A}^{2}}, v_{A} = \sqrt{\frac{G M}{r_{A}}} = 7 548.6 m/s$

Calculamos la velocidad en el perigeo A y en el apogeo C de la trayectoria elíptica que une A y C. Sea r₁=r_A y r₂=r_C

$\begin{array}{l} v_{1} = \sqrt{\frac{2 G M r_{C}}{r_{A} (r_{A} + r_{C})}} = 10 502 m/s \\ v_{2} = \sqrt{\frac{2 G M r_{A}}{r_{C} (r_{A} + r_{C})}} = 350.1 m/s \end{array}$

El tiempo que tarda en viajar de A a C es medio periodo

$P_{1} = π \sqrt{\frac{a_{1}^{3}}{G M},} a_{1} = \frac{r_{A} + r_{C}}{2}$

P₁=49.3831 horas

Calculamos la velocidad en el apogeo C y en el perigeo B de la trayectoria elíptica que une C y B.

$\begin{array}{l} v_{3} = \sqrt{\frac{2 G M r_{B}}{r_{C} (r_{C} + r_{B})}} = 1125.3 m/s \\ v_{4} = \sqrt{\frac{2 G M r_{C}}{r_{B} (r_{C} + r_{B})}} = 2250.5 m/s \end{array}$

El tiempo que tarda en viajar de C a B es medio periodo

$P_{2} = π \sqrt{\frac{a_{2}^{3}}{G M},} a_{2} = \frac{r_{C} + r_{B}}{2}$

P₂=86.3684 horas

El tiempo total de viaje es P₁+P₂=135.8 horas

El valor absoluto del cambio de velocidad es proporcional al combustible gastado

Cambio de velocidad en A, al pasar la nave espacial de la órbita circular a la órbita elíptica de transferencia que une A y C

Δv₁=|v₁-v_A|=2 953.1 m/s

Cambio de velocidad en C, al pasar la nave espacial de la primera órbita elíptica de transferencia a la segunda

Δv₂=|v₃-v₂|=775.2 m/s

Cambio de velocidad en B, al pasar la nave espacial de la órbita elíptica de transferencia a la órbita circular

Δv₃=|v_B-v₄|=301.5 m/s

Cambio de velocidad total

Δv=Δv₁+Δv₂+Δv₃=4 029.9 m/s

Para el trazado de las órbitas se ha tomado el radio R de la Tierra como unidad

M=5.98e24; %masa de la Tierra
G=6.67e-11; %constante G
R=6.37e6; %radio de la Tierra

rA=7e6; %radio de órbita circular interior
rB=105e6; %radio de la órbita circular exterior
rC=210e6; %apogeo
vA=sqrt(G*M/rA); %velocidad en la órbita circular interior
vB=sqrt(G*M/rB); %velocidad en la órbita circular exterior
v1=sqrt(2*G*M*rC/(rA*(rA+rC))); %salida de la órbita circular interior
v2=sqrt(2*G*M*rA/(rC*(rA+rC))); %llegada al apogeo
DV_1=abs(v1-vA); %impulso en el perigeo A
v3=sqrt(2*G*M*rB/(rC*(rB+rC))); %salida del apogeo C
v4=sqrt(2*G*M*rC/(rB*(rB+rC))); %llegada a la órbita circular exterior
DV_2=abs(v3-v2); %impulso en el apogeo C
DV_3=abs(vB-v4); %impulso en la órbita circular exterior
%semiejes mayores de la primera y segunda elipse
a1=(rA+rC)/2;
a2=(rB+rC)/2;
%tiempos de viaje
P1=pi*sqrt(a1^3/(G*M));  %medio periodo
P2=pi*sqrt(a2^3/(G*M));  %medio periodo
fprintf('Velcidades en las órbitas circulares: vA: %5.1f, vB: %5.1f\n',vA,vB);
fprintf('órbita de transferencia 1, v1: %5.1f, v2: %5.1f\n',v1,v2);
fprintf('órbita de transferencia 2, v3: %5.1f, v4: %5.1f\n',v3,v4);
fprintf('Cambio de velocidad, Dv: %5.1f\n',DV_1+DV_2+DV_3);
fprintf('Tiempo de viaje (horas), P: %5.1f\n',(P1+P2)/3600);

hold on
fplot(@(x) (rA/R)*cos(x), @(x) (rA/R)*sin(x),[0,2*pi],'color','b')
fplot(@(x) (rB/R)*cos(x), @(x) (rB/R)*sin(x),[0,2*pi],'color','r')
%primera órbita elíptica
ex=(a1-rA)/a1; %excentricidad
d=a1*(1-ex^2);
r=@(x) (d/R)./(1+ex*cos(x));
fplot(@(x) r(x).*cos(x), @(x) r(x).*sin(x),[0,pi],'lineStyle','--','color','k') 
%segunda órbita elíptica
ex=(a2-rB)/a2; %excentricidad
d=a2*(1-ex^2);
r=@(x) (d/R)./(1+ex*cos(x));
fplot(@(x) r(x).*cos(x), @(x) r(x).*sin(x),[pi,2*pi],'lineStyle','--','color','k') 
hold off
axis equal
grid on
xlabel('x')
ylabel('y')
title('Dos órbitas de transferencia')

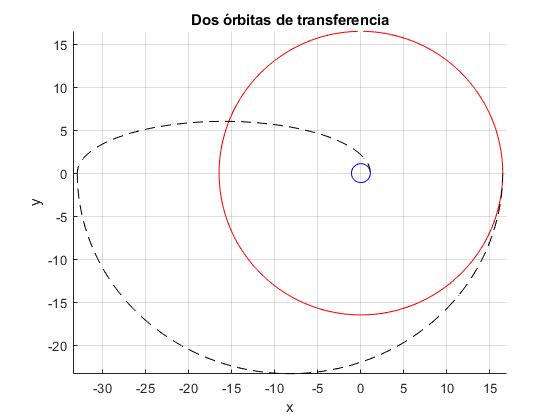
Velcidades en las órbitas circulares: vA: 7548.6, vB: 1949.0
órbita de transferencia 1, v1: 10501.7, v2: 350.1
órbita de transferencia 2, v3: 1125.3, v4: 2250.5
Cambio de velocidad, Dv: 4029.9
Tiempo de viaje (horas), P: 135.8

Transferencia de Hohmann

En este caso, empleamos una órbita elíptica de transferencia que une A y B

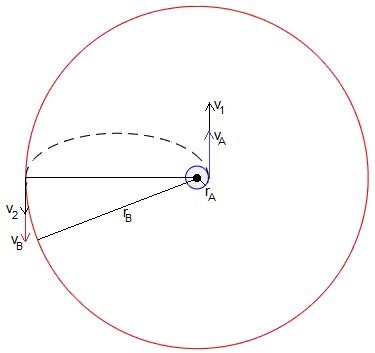
Orbita circular interior de radio r_A

$v_{A} = \sqrt{\frac{G M}{r_{A}}} = 7 548.6 m/s$

La velocidad en el perigeo A y en el apogeo B de la órbita elíptica que une A y B.

$\begin{array}{l} v_{1} = \sqrt{\frac{2 G M r_{B}}{r_{A} (r_{A} + r_{B})}} = 10 336 m/s \\ v_{2} = \sqrt{\frac{2 G M r_{A}}{r_{B} (r_{A} + r_{B})}} = 689.1 m/s \end{array}$

El tiempo empleado en la transferencia entre las dos órbitas circulares es medio periodo

$P = π \sqrt{\frac{a^{3}}{G M},} a = \frac{r_{B} + r_{A}}{2}$

P=18.31 horas

El valor absoluto del cambio de velocidad es proporcional al combustible gastado

Cambio de velocidad en A, al pasar la nave espacial de la órbita circular a la órbita elíptica de transferencia

Δv₁=|v₁-v_A|=2 787.7 m/s

Cambio de velocidad en B, al pasar la nave espacial de la órbita elíptica de transferencia a la órbita circular

Δv₂=|v_B-v₂|=1 259.9 m/s

Cambio de velocidad total

Δv=Δv₁+Δv₂=4 047.7 m/s

Para el trazado de las órbitas se ha tomado el radio R de la Tierra como unidad

M=5.98e24; %masa de la Tierra
G=6.67e-11; %constante G
R=6.37e6; %radio de la Tierra
r1=7e6; %órbita exterior 
r2=105e6;  %órbita interior  

vA=sqrt(G*M/r1); %velocidad en la órbita circular interior
vB=sqrt(G*M/r2); %velocidad en la órbita circular exterior

%velocidad de salida de la órbita interior
v1=sqrt(2*G*M*r2/(r1*(r1+r2)));
%velocidad de llegada a la órbita exterior
v2=r1*v1/r2; 
DV_1=abs(v1-vA); %impulso en el perigeo A
DV_2=abs(v2-vB); %impulso en el apogeo B
%tiempos de viaje
a=(r1+r2)/2;
P=pi*sqrt(a^3/(G*M));  %medio periodo
fprintf('Velcidades en las órbitas circulares: vA: %5.1f, vB: %5.1f\n',vA,vB);
fprintf('órbita de transferencia v1: %5.1f, v2: %5.1f\n',v1,v2);
fprintf('Cambio de velocidad, Dv %5.1f \n',DV_1+DV_2);
fprintf('Tiempo de viaje (horas), P: %5.1f\n',P/3600);

hold on
fplot(@(x) (r1/R)*cos(x), @(x) (r1/R)*sin(x),[0,2*pi],'color','b')
fplot(@(x) (r2/R)*cos(x), @(x) (r2/R)*sin(x),[0,2*pi],'color','r')
%órbita elíptica
ex=1-r1/a; %excentricidad
d=a*(1-ex^2);
r=@(x) (d/R)./(1+ex*cos(x));
fplot(@(x) r(x).*cos(x), @(x) r(x).*sin(x),[0,pi],'lineStyle','--','color','k') 
hold off
axis equal
grid on
xlabel('x')
ylabel('y')
title('Orbita de transferencia')

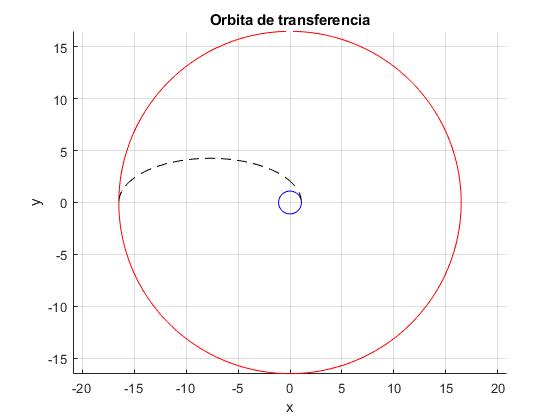
Velcidades en las órbitas circulares: vA: 7548.6, vB: 1949.0
órbita de transferencia v1: 10336.3, v2: 689.1
Cambio de velocidad, Dv 4047.7 
Tiempo de viaje (horas), P:  18.3

Comparación

Con los datos de este ejemplo, se obtienen resultados similares para Δv, pero completamente diferentes para el tiempo de tránsito de una órbita circular a la otra, 135.8 h frente a 18.3 h.

Vamos a hacer un estudio más general que nos permita comparar el cambio de velocidad Δv con una órbita elíptica de transferencia y el cambio de velocidad Δv para dos órbitas elípticas de transferencia.

Para una órbita elíptica de taransferencia expresamos Δv/v_A en términos del cociente x=r_B/r_A

$\begin{array}{l} v_{1} = \sqrt{\frac{2 G M r_{B}}{r_{A} (r_{B} + r_{A})}} = \sqrt{\frac{G M}{r_{A}}} \sqrt{\frac{2 \frac{r_{B}}{r_{A}}}{1 + \frac{r_{B}}{r_{A}}}} = v_{A} \sqrt{\frac{2 x}{1 + x}} \\ v_{2} = \sqrt{\frac{2 G M r_{A}}{r_{B} (r_{A} + r_{B})}} = v_{A} \sqrt{\frac{2}{x (1 + x)}} \\ v_{B} = \sqrt{\frac{G M}{r_{B}}} = v_{A} \sqrt{\frac{r_{A}}{r_{B}}} = \frac{v_{A}}{\sqrt{x}} \end{array}$

El cambio de velocidad es

${(\frac{Δ v}{v_{A}})}_{1} = | v_{1} - v_{A} | + | v_{2} - v_{B} | = | \sqrt{\frac{2 x}{1 + x}} - 1 | + | \sqrt{\frac{2}{x (1 + x)}} - \frac{1}{\sqrt{x}} |$

Para dos órbita elíptica de taransferencia expresamos Δv/v_A en términos del cociente x=r_B/r_A y k=r_C/r_A

$\begin{array}{l} v_{1} = \sqrt{\frac{2 G M r_{C}}{r_{A} (r_{A} + r_{C})}} = v_{A} \sqrt{\frac{2 k}{1 + k}} \\ v_{2} = \sqrt{\frac{2 G M r_{A}}{r_{C} (r_{A} + r_{C})}} = v_{A} \sqrt{\frac{2}{k (1 + k)}} \\ v_{3} = \sqrt{\frac{2 G M r_{B}}{r_{C} (r_{C} + r_{B})}} = v_{A} \sqrt{\frac{2 x}{k (k + x)}} \\ v_{4} = \sqrt{\frac{2 G M r_{C}}{r_{B} (r_{C} + r_{B})}} = v_{A} \sqrt{\frac{2 k}{x (k + x)}} \end{array}$

El cambio de velocidad es

$\begin{array}{l} {(\frac{Δ v}{v_{A}})}_{2} = | v_{1} - v_{A} | + | v_{3} - v_{2} | + | v_{4} - v_{B} | = \\ | \sqrt{\frac{2 k}{1 + k}} - 1 | + | \sqrt{\frac{2 x}{k (k + x)}} - \sqrt{\frac{2}{k (1 + k)}} | + | \sqrt{\frac{2 k}{x (k + x)}} - \frac{1}{\sqrt{x}} | \end{array}$

Cuando C está muy alejado k→∞, El cambio de velocidad se expresa

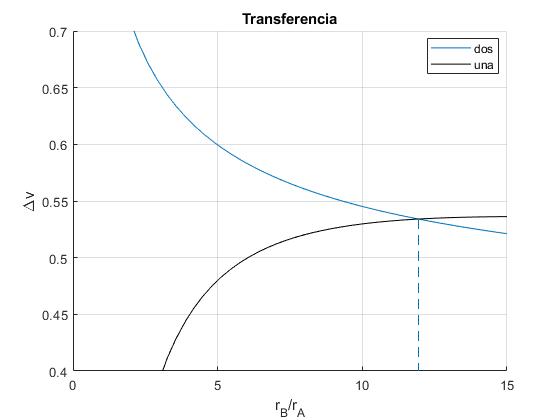
${(\frac{Δ v}{v_{A}})}_{2} = \sqrt{2} - 1 + \sqrt{\frac{2}{x}} - \frac{1}{\sqrt{x}}$

Representamos en la misma gráfica

(Δv/v_A)₁ para una órbita elíptica de transferencia
(Δv/v_A)₂ para dos órbitas elípticas de transferencia para k→∞

hold on
f=@(x) sqrt(2)-1+sqrt(2./x)-1./sqrt(x); %dos órbitas
fplot(f,[1,15])
g=@(x) abs(sqrt(2*x./(1+x))-1)+abs(sqrt(2./(x.*(1+x)))-1./sqrt(x)); %una órbita
fplot(g,[1,15],'color','k')
line([11.94,11.94],[0,g(11.94)],'lineStyle','--')
hold off
ylim([0.4,0.7])
xlabel('r_B/r_A')
ylabel('\Deltav')
legend('dos','una','Location','best')
grid on
title('Transferencia')

Comprobamos con Data tips que el punto de intersección es r_B/r_A=11.94. Calculamos la raiz de la función transcendente con fzero de MATLAB

${(\frac{Δ v}{v_{A}})}_{2} - {(\frac{Δ v}{v_{A}})}_{1} = {\sqrt{2} - 1 + \sqrt{\frac{2}{x}} - \frac{1}{\sqrt{x}}} - {| \sqrt{\frac{2 x}{1 + x}} - 1 | + | \sqrt{\frac{2}{x (1 + x)}} - \frac{1}{\sqrt{x}} |} = 0$

>> h=@(x) f(x)-g(x);
>> raiz=fzero(h,[10,12])
raiz =   11.9388

Para r_B/r_A<11.94, es más eficiente una órbita elíptica de transferencia. Para r_B/r_A>11.94, es más eficiente dos órbitas de transferencia

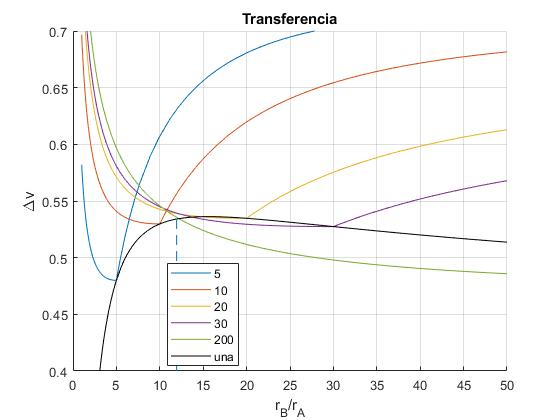
Representamos en la misma gráfica

(Δv/v_A)₁ para una órbita elíptica de transferencia (color negro)
(Δv/v_A)₂ para dos órbitas elípticas de transferencia para k=5, 10, 20, 30, 200 (en varios colores)

hold on
for k=[5,10,20,30,200]
    f=@(x) abs(sqrt(2*k/(1+k))-1)+abs(sqrt(2/(k*(1+k)))-
sqrt(2*x./(k*(k+x))))+abs(sqrt(2*k./(x.*(k+x)))-1./sqrt(x));
    fplot(f,[1,50])
end
g=@(x) abs(sqrt(2*x./(1+x))-1)+abs(sqrt(2./(x.*(1+x)))-1./sqrt(x));
fplot(g,[1,50],'color','k')
line([11.94,11.94],[0,g(11.94)],'lineStyle','--')
hold off
ylim([0.4,0.7])
xlabel('r_B/r_A')
ylabel('\Deltav')
legend('5','10','20','30','200','una','Location','best')
grid on
title('Transferencia')

Referencias

Howard D. Curtis. Orbital Mechanics for Engineering Students. Elsevier, págs. 308-312