Un astronauta envía un objeto a otro

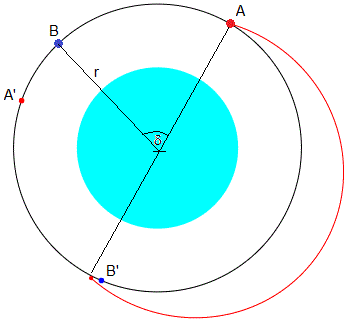
Como vemos en la figura, el primer astronauta lanza el objeto en la posición A, cuando el segundo astronauta está en la posición B, retrasado un ángulo δ. El objeto describe una trayectoria elíptica (en color rojo) cuyo foco está en el centro de la Tierra. A y B se mueven en su órbita circular con velocidad constante. Cuando el objeto llega a la órbita circular, las posiciones de los astronautas son A' y B'.

El programa interactivo al final de esta página, se ha planteado como un juego en el que se trata de que el astronauta B recoja la herramienta lanzada por el astronauta A en el menor número de intentos posible. Cuando el objeto llega a las proximidades del astronauta B, el programa se detiene y aparece un icono que anuncia el éxito en el intento.

Orbita circular

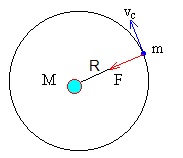
Una nave espacial describe una órbita circular de radio R alrededor de la Tierra con velocidad constante v_c, que se calcula aplicando la dinámica del movimiento circular.

$m \frac{v_{c}^{2}}{R} = \frac{G M m}{R} v_{c} = \sqrt{\frac{G M}{R}}$

Trayectoria del objeto

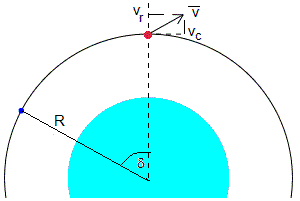
Cuando al objeto se le proporciona una velocidad radial v_r, el momento angular y la energía valen

$\begin{array}{l} L = m R v_{c} \\ E = \frac{1}{2} m (v_{r}^{2} + v_{c}^{2}) - \frac{G M m}{R} = \frac{1}{2} m v_{r}^{2} - \frac{1}{2} \frac{G M m}{R} \end{array}$

que se mantienen constantes en todos los puntos de la trayectoria.

La ecuación de la trayectoria en coordenadas polares es

$r = \frac{d}{1 + ε \cos θ} ε = \sqrt{1 + \frac{2 L^{2} E}{G^{2} M^{2} m^{3}}} = \frac{v_{r}}{v_{c}} d = \frac{L^{2}}{G M m^{2}} = R$

Para que la órbita sea elíptica ε<1, v_r<v_c

Como se ha estudiado en la página titulada Trayectoria de un proyectil disparado desde la superficie de la Tierra, el objeto sale de la posición R, θ₀ y llega a la posición R, -θ₀, donde

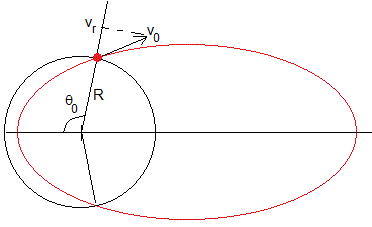
$R = \frac{d}{1 + ε \cos θ_{0}} \cos θ_{0} = \frac{d - R}{R ε} = 0 θ_{0} = \frac{π}{2}$

El objeto sale en la posición angular θ₀=π/2 y llega 2π-θ₀=3π/2. Su desplazamiento angular es π, tal como vemos en la primera figura de esta página

Conocidos los parámetros d y ε, se calculan

El semieje mayor a, que es la media aritmética de los radios mínimo (θ=0) y máximo (θ=π) de la elipse.

$2 a = \frac{d}{1 + ε} + \frac{d}{1 - ε} a = \frac{d}{1 - ε^{2}} = R \frac{v_{c}^{2}}{v_{c}^{2} - v_{r}^{2}}$

La semidistancia focal c=ε·a

$c = ε a = R \frac{v_{c} v_{r}}{v_{c}^{2} - v_{r}^{2}}$

El semieje menor b de la elipse

$b = \sqrt{a^{2} - c^{2}} = R \frac{v_{c}}{\sqrt{v_{c}^{2} - v_{r}^{2}}}$

Tiempo de vuelo, aplicando la constancia del momento angular

En la página titulada Trayectoria de un proyectil disparado desde la superficie de la Tierra, obtuvimos la expresión del tiempo T de vuelo del proyectil disparado desde la superficie de la Tierra, aplicando la constancia del momento angular

$\begin{array}{l} A r e a = \frac{a b}{2} (\frac{π}{2} - z_{1} - \frac{1}{2} \sin 2 z_{1}) - \frac{R^{2} \sin 2 θ_{0}}{4} \\ a \sin z_{1} = - c - R \cos θ_{0} \\ T = 2 \frac{2 m \cdot A r e a}{L} \end{array}$

Como θ₀=π/2, introduciendo las expresiones del semieje mayor a, menor b y semidistancia focal c en términos de v_r y v_c

$\begin{array}{l} A r e a = \frac{a b}{2} (\frac{π}{2} - z_{1} - \sin z_{1} \cos z_{1}) \\ \sin z_{1} = - \frac{v_{r}}{v_{c}} \end{array}$

Llamando cosα=v_r/v_c

$\begin{array}{l} z_{1} = - \frac{π}{2} + α \\ A r e a = \frac{1}{2} R \frac{v_{c}^{2}}{v_{c}^{2} - v_{r}^{2}} R \frac{v_{c}}{\sqrt{v_{c}^{2} - v_{r}^{2}}} (\frac{π}{2} - (- \frac{π}{2} + α) - (- \frac{v_{r}}{v_{c}} \sqrt{1 - {(\frac{v_{r}}{v_{c}})}^{2}})) \\ T = \frac{4 \cdot A r e a}{R v_{c}} = 2 R \frac{(π - α) v_{c}^{2} + v_{r} \sqrt{v_{c}^{2} - v_{r}^{2}}}{{(v_{c}^{2} - v_{r}^{2})}^{3 / 2}} \end{array}$

Aplicando la ecuación de Kepler

La ecuación de Kepler nos permite calcular la posición de un cuerpo celeste en un instante dado, o bien, el instante t en que el cuerpo celeste se encuentra en una determinada posición θ. En la página titulada El problema de Kepler se proporcionan ejemplos de ambos.

Calculamos el instante t₀ cuando se lanza el objeto desde la posición θ=π/2. Después calculamos el instante t₁ cuando el objeto alcanza la órbita circular de los astronautas, en la posición θ=2π-π/2=3π/2. El tiempo de vuelo es,T=t₁-t₀

Partimos de las expresiones sinE y cosE, deducidas en la página titulada El problema de Kepler

$\begin{array}{l} \sin E = \frac{\sqrt{1 - ε^{2}} \sin θ}{1 + ε \cos θ} \\ \cos E = \frac{ε + \cos θ}{1 + ε \cos θ} \end{array}$

Calculamos los ángulos E₀ y E₁

$\begin{array}{l} θ = \frac{π}{2} \to \sin E_{0} = \sqrt{1 - {(\frac{v_{r}}{v_{c}})}^{2}} \cos E_{0} = \frac{v_{r}}{v_{c}} E_{0} = \arccos (\frac{v_{r}}{v_{c}}) \\ θ = \frac{3 π}{2} \to \sin E_{1} = - \sqrt{1 - {(\frac{v_{r}}{v_{c}})}^{2}} \cos E_{1} = \frac{v_{r}}{v_{c}} \end{array}$

Llamando α=E₀=arccos(v_r/v_c), E₁=2π-α

Sustituyendo en la ecuación de Kepler, $M_{e} = E - ε \sin E$ , obtenemos M_e. Conocido M_e obtenemos el tiempo t.

$t = \frac{E - ε \sin E}{2 π} 2 π \sqrt{\frac{a^{3}}{G M}} = R v_{c} \frac{v_{c} E - v_{r} \sin E}{{(v_{c}^{2} - v_{r}^{2})}^{3 / 2}}$

Conocidos los ángulos E₀ y E₁, calculamos el tiempo de vuelo T

$T = t_{1} - t_{0} = R v_{c} \frac{v_{c} (E_{1} - E_{0}) - v_{r} (\sin E_{1} - \sin E_{0})}{{(v_{c}^{2} - v_{r}^{2})}^{3 / 2}} = 2 R \frac{v_{c}^{2} (π - α) + v_{r} \sqrt{v_{c}^{2} - v_{r}^{2}}}{{(v_{c}^{2} - v_{r}^{2})}^{3 / 2}}$

Llegamos a la misma expresión del tiempo de vuelo que aplicando la constancia del momento angular

Los astronautas describen una órbita circular de 1000 km de altura, el primero lanza un objeto con velocidad de v_r=1000 m/s en la dirección radial. El tiempo de vuelo del objeto hasta que alcanza la trayectoria circular es T=3795 s

M=5.98e24; %masa de la Tierra
G=6.67e-11; %constante G

R=6.37e6+1e6; %1000 km de altura
vr=1000; %velocidad radial
vc=sqrt(G*M/R); %velocidad órbita circular

T=2*R*(vc^2*(pi-acos(vr/vc))+vr*sqrt(vc^2-vr^2))
/(sqrt(vc^2-vr^2))^3; %tiempo de vuelo
fprintf('El tiempo de vuelo (s) es %4.1f\n',T)

El tiempo de vuelo (s) es 3795.0

El segundo astronauta recoge el objeto

El objeto tarda un tiempo T desde que es lanzado por el primer astronauta hasta que llega al segundo. El desplazamiento angular del segundo astronauta es π+δ, el arco de circunferencia que recorre a velocidad constante v_c es R(π+δ), luego para que se produzca el encuentro, la velocidad radial v_r con la que se deberá lanzar el objeto será solución de la ecuación

$\begin{array}{l} R \frac{π + δ}{v_{c}} = T \\ \frac{π + δ}{v_{c}} = 2 \frac{v_{c}^{2} (π - α) + v_{r} \sqrt{v_{c}^{2} - v_{r}^{2}}}{{(v_{c}^{2} - v_{r}^{2})}^{3 / 2}} \end{array}$

Dado el ángulo de retraso del segundo astronauta respecto del primero, δ y la velocidad v_c de los astronautas, obtenemos v_r de dicha ecuación trascendente.

Los astronautas describen una órbita circular de 5000 km de altura, el segundo astronauta está retrasado 30° (π/6) respecto del primero. Este lanza un objeto con velocidad v_r=672 m/s en la dirección radial para que sea recogido por el segundo

M=5.98e24; %masa de la Tierra
G=6.67e-11; %constante G

h=5e6; %5000 km de altura
R=6.37e6+h; 
delta=pi/6;
vc=sqrt(G*M/R); %velocidad órbita circular

f=@(x) 2*(vc^2*(pi-acos(x/vc))+x*sqrt(vc^2-x^2))/(vc^2-x^2)^(3/2)-
(pi+delta)/vc;
vr=fzero(f,vc/4)

vr =  672.2249

El problema admite más de una solución, por ejemplo, el primer astronuata puede lanzar el objeto con una velocidad radial v_r mayor de modo que el segundo recoja el objeto después de haber dado una vuelta completa

$\frac{2 π + π + δ}{v_{c}} = 2 \frac{v_{c}^{2} (π - α) + v_{r} \sqrt{v_{c}^{2} - v_{r}^{2}}}{{(v_{c}^{2} - v_{r}^{2})}^{3 / 2}}$

M=5.98e24; %masa de la Tierra
G=6.67e-11; %constante G

h=5e6; %5000 km de altura
R=6.37e6+h; 
delta=pi/6;
vc=sqrt(G*M/R); %velocidad órbita circular
f=@(x) 2*(vc^2*(pi-acos(x/vc))+x*sqrt(vc^2-x^2))/(vc^2-x^2)^(3/2)-
(2*pi+pi+delta)/vc;
vr=fzero(f,vc/4)

vr =   3.4536e+03

También podemos lanzarlo con velocidad aún mayor, de modo que el segundo astronauta recoja el objeto después de dos vueltas y así, sucesivamente sin superar el límite v_c=5923 m/s

M=5.98e24; %masa de la Tierra
G=6.67e-11; %constante G

h=5e6; %5000 km de altura
R=6.37e6+h; 
delta=pi/6;
vc=sqrt(G*M/R); %velocidad órbita circular
for n=0:3
    f=@(x) 2*(vc^2*(pi-acos(x/vc))+x*sqrt(vc^2-x^2))/(vc^2-x^2)^(3/2)-
(2*n*pi+pi+delta)/vc;
    vr=fzero(f,vc/4);
    if vr>vc
        break;
    end
    fprintf('vuelta %i, velocidad radial, %5.1f m/s\n',n,vr)
end

vuelta 0, velocidad radial, 672.2 m/s
vuelta 1, velocidad radial, 3453.6 m/s
vuelta 2, velocidad radial, 4193.9 m/s
vuelta 3, velocidad radial, 4555.0 m/s

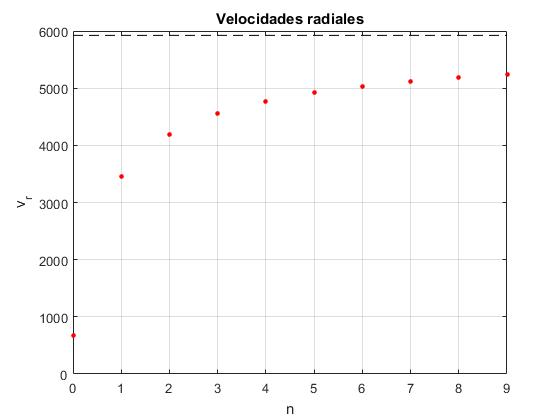
Añadimos unas líneas de código para representar las velocidades radiales calculadas y la velocidad en la órbita circular v_c en forma de línea a trazos

....
    vr=zeros(1,10);
for n=0:9
    f=@(x) 2*(vc^2*(pi-acos(x/vc))+x*sqrt(vc^2-x^2))/(vc^2-x^2)^(3/2)
-(2*n*pi+pi+delta)/vc;
    vr(n+1)=fzero(f,vc/4);
    if vr(n+1)>vc
        break;
    end
end
plot(0:9,vr,'o','markersize',3,'markeredgecolor','r','markerfacecolor','r')
line([0,9],[vc,vc], 'color','k','lineStyle','--')
grid on
xlabel('n')
ylabel('v_r')
title('Velocidades radiales')

Actividades

El programa interactivo, genera una número aleatorio entre 0 y 90, que representa el ángulo δ en grados de retraso del segundo astronuata respecto del primero

Se introduce

La altura en km de la órbita circular de los astronautas, en el control titulado Altura
La velocidad radial v_r que proporciona el primer astronuata al objeto, en el control titulado Velocidad radial

Se pulsa el botón titulado Nuevo

Observamos los dos astronautas identificados por colores, rojo el primero y azul el segundo. El segundo retrasado un ángulo que se proporciona en la esquina superior izquierda. Se dibuja el vector velocidad en la posición que ocupa el primer astronauta

Los astronautas empiezan a moverse alrededor de la Tierra siguiendo la órbita circular cuando se pulsa el botón titulado ► con la velocidad, que se especifica en la esquina superior izquierda

Se pulsa el botón titulado Lanza para que el primer astronauta proporcione un impulso en la dirección radial al objeto. Observamos la trayectoria del objeto hasta que alcanza la órbita circular

Si el segundo astronauta logra recoger el objeto, el programa se detiene mostrando el icono de éxito

Si no se ha tenido éxito, se cambia la velocidad radial v_r, se pulda el botón titulado Nuevo, a continuación ► y finalmente, Lanza

Ejemplo

Supongamos que hemos elegido una altura de 5000 km, la velocidad de los astronautas en su órbita circular es v_c=5923 m/s. El programa interactivo ha generado un ángulo de retraso δ=25.7° del segundo astronuata (azul) respecto del primero (rojo). Hemos calculado con un script de MATLAB las velocidades radiales v_r que proporciona el primer astronauta para que el segundo recoja el objeto

vuelta 0, velocidad radial, 587.0 m/s
vuelta 1, velocidad radial, 3439.8 m/s
vuelta 2, velocidad radial, 4188.1 m/s
vuelta 3, velocidad radial, 4551.8 m/s

Altura (km):
Velocidad radial (m/s):

Referencias

Francisco G. M. Orlando, C. Farina, Carlos A. D. Zarro. Kepler's equation and some of its pearls. Am. J. Phys. 86 (11) November 2018, pp. 849-858