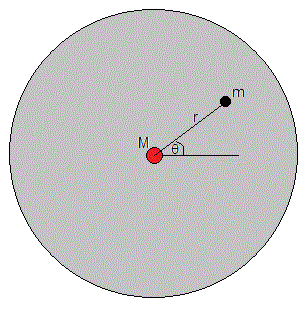
Supongamos un planeta de masa M que está rodeado de una capa de polvo, de densidad uniforme ρ. Un satélite artificial de masa m se mueve alrededor del planeta. Vamos a estudiar su movimiento bajo la fuerza de atracción del planeta y de la capa de polvo. No consideraremos el posible rozamiento del satélite al chocar con las partículas de polvo

La fuerza de atracción del planeta es inversamente proporcional al cuadrado de la distancia

${\displaystyle G\frac{Mm}{r^2}}$

Demostramos en la página titulada La aceleración de la gravedad en el interior y en el exterior de una distribución esférica y uniforme de masa que la fuerza de atracción de un distribución esférica y uniforme de masa ejerce sobre una partícula situada a una distancia r del centro, es la que ejercería sobre dicha partícula, la masa contenida en una esfera concéntrica de radio r.

${\displaystyle Gm\left(\rho \frac{4}{3}\pi r^3\right)\frac{1}{r^2}=\frac{4}{3}\pi Gm\rho r}$

El satélite se mueve bajo la acción de dos fuerzas centrales, una inversamente proporcional al cuadrado de la distancia r, y otra más pequeña, proporcional a la distancia r al centro fijo de fuerzas. Las ecuaciones del movimiento en coordendas polares son

${\displaystyle \begin{array}{l}m\left(\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2\right)=-GMm\frac{1}{r^2}-\frac{4}{3}\pi Gm\rho r\hfill \\ m\left(r\frac{d^2\theta }{d{t}^2}+2\frac{d\theta }{dt}\frac{dr}{dt}\right)=0\hfill \end{array}}$

La segunda ecuación nos indica que el momento angular L, expresado en coordenadas polares, es constante

${\displaystyle \frac{d}{dt}\left(m{r}^2\frac{d\theta }{dt}\right)=0L=m{r}^2\frac{d\theta }{dt}=\text{cte}}$

Teniendo en cuenta la constancia del momento angular L, escribimos la ecuación diferencial que describe el movimiento en la dirección radial

${\displaystyle \frac{d^{2}r}{d{t}^2}=\frac{L^2}{m^2{r}^3}-GM\frac{1}{r^2}-\frac{4}{3}\pi G\rho r}$

Escribimos esta ecuación en términos de la densidad relativa del polvo k=ρ/ρ_T respecto de la densidad del planeta y del radio del planeta r_T. Recordando que la masa del planeta M es

${\displaystyle M={\rho }_T\left(\frac{4}{3}\pi r_T^3\right)}$

El sistema de ecuaciones diferenciales que tenemos que resolver es

${\displaystyle \begin{array}{l}\frac{d^{2}r}{d{t}^2}=\frac{L^2}{m^2{r}^3}-GM\left(\frac{1}{r^2}+k\frac{r}{r_T^3}\right)\\ \frac{d\theta }{dt}=\frac{L}{m{r}^2}\end{array}}$

Ecuaciones de Lagrange

La fuerza de atracción -GMm/r² es conservativa y su energía potencial es -GMm/r. La fuerza atractiva -4πGρr/3 es similar a la fuerza que ejerce una muelle elástico -kx sobre una partícula, la energía potencial de esta fuerza es kx²/2. Por tanto, la fórmula de la energía potencial para esa fuerza es 2πGρr²/3

La energía cinética en coordenadas polares y la energía potencial del satélite de masa m son

${\displaystyle \begin{array}{l}{E}_k=\frac{1}{2}m\left\{{\left(\frac{dr}{dt}\right)}^2+r^2{\left(\frac{d\theta }{dt}\right)}^2\right\}\\ E_p=-G\frac{Mm}{r}+\frac{1}{2}\left(\frac{4}{3}\pi Gm\rho \right)r^2\end{array}}$

La energía total es la suma de las dos cantidades. La lagrangiana L (no confundir con el momento angular) es la diferencia

${\displaystyle \begin{array}{l}L=\frac{1}{2}m\left\{{\left(\frac{dr}{dt}\right)}^2+r^2{\left(\frac{d\theta }{dt}\right)}^2\right\}+G\frac{Mm}{r}-\frac{1}{2}\left(\frac{4}{3}\pi Gm\rho \right)r^2\\ \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ \frac{d}{dt}\left(m{r}^2\frac{d\theta }{dt}\right)=0\\ \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{r}}\right)-\frac{\partial L}{\partial r}=0\\ m\frac{d^{2}r}{d{t}^2}-mr{\left(\frac{d\theta }{dt}\right)}^2+G\frac{Mm}{r^2}+\left(\frac{4}{3}\pi Gm\rho \right)r=0\end{array}}$

Obtenemos las mismas ecuaciones

Resolvemos el sistema de dos ecuaciones diferenciales, con las siguientes condiciones iniciales: en el instante t=0, r=r₀, dr/dt=0.

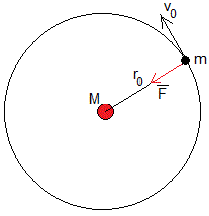
Nos queda determinar el valor del momento angular L que es una constante del movimiento. Supondremos que el satélite describe una órbita circular de radio r₀ alrededor del planeta de masa M, no cubierto de la nube de polvo.

Su velocidad v₀, se obtiene de la ecuación de la dinámica del movimiento circular

${\displaystyle m\frac{v_0^2}{r_0}=G\frac{Mm}{r_0^2}{v}_0=\sqrt{\frac{GM}{r_0}}}$

El momento angular L será

${\displaystyle L=m{r}_0{v}_0\sin 90=m\sqrt{GM{r}_0}}$

De esto modo, comprobaremos cómo se modifica la órbita circular del satélite artificial por el efecto de la nube de polvo.

Escalas

Consideraremos que el planeta es la Tierra, cuya masa M=5.98·10²⁴ kg y cuyo radio es r_T=6.37·10⁶ m. La constante G=6.67·10^-11 Nm²/kg². Para efectuar los cálculos, establecemos un sistema de unidades de modo que el tiempo τ se mide en horas, t=3600·τ, y la distancia R en unidades de 1000 km, r=10⁶R. Las ecuaciones del movimiento se escriben

${\displaystyle \begin{array}{l}\{\begin{array}{l}\frac{{10}^6}{{3600}^2}\frac{d^{2}R}{d{\tau }^2}=GM\frac{1}{{10}^{12}}\left\{\frac{R_0}{R^3}-\frac{1}{R^2}-k\frac{R}{R_T^3}\right\}\\ \frac{d\theta }{3600·d\tau }=\sqrt{GM}\frac{\sqrt{R_0}}{R^2}\frac{{10}^3}{{10}^{12}}\end{array}\\ \{\begin{array}{l}\frac{d^{2}R}{d{\tau }^2}=5169.3\left\{\frac{R_0}{R^3}-\frac{1}{R^2}-k\frac{R}{R_T^3}\right\}\\ \frac{d\theta }{d\tau }=71.89787\frac{\sqrt{R_0}}{R^2}\end{array}\end{array}}$

Resolvemos el sistema de ecuaciones diferenciales, con las siguientes condiciones iniciales: en el instante τ=0, R=R₀ y dR/dτ=0

RT=6.37; %radio de la Tierra
R0=8; %Posición inicial del satálite 
k=0.05; %densidad relativa del polvo

x0=[R0,0,0];	%condiciones iniciales
%x(1) es r, x(2) es dr/dt, x(3) es theta
fg=@(t,x) [x(2);5169.303*(R0/x(1)^3-1/x(1)^2-k*x(1)/RT^3);
71.89787*sqrt(R0)/x(1)^2];
[t,x]=ode45(fg,[0,4],x0);
plot(x(:,1).*cos(x(:,3)), x(:,1).*sin(x(:,3)))
grid on
axis equal
xlabel('x')
ylabel('y')
title('Movimiento en una nube')

figure
subplot(2,1,1)
plot(t,x(:,1))
grid on
xlabel('\tau')
ylabel('R')
subplot(2,1,2)
plot(t,x(:,3))
for i=1:floor(x(end,3)/(2*pi))
    line([0,t(end)],[i*2*pi,i*2*pi],'lineStyle','--','color','k')
end
grid on
xlabel('\tau')
ylabel('\theta')

Se representa la trayectoria hasta el instante τ=4

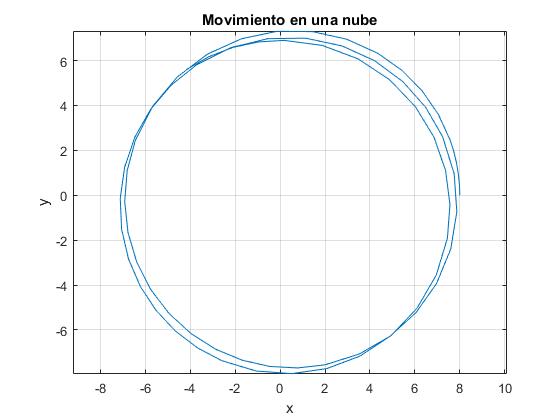
Si no hubiese polvo de densidad relativa k, el satélite describiría una órbita circular de radio R₀=8, con un periodo

${\displaystyle P_{\theta }=\frac{2\pi r_0}{v_0}=2\pi \sqrt{\frac{r_0^3}{GM}}}$

Con r₀=10⁶R₀. En las unidades que hemos establecido, P_θ=1.9774 horas

Comprobamos que la energía del satélite se mantiene constante, véase el apartado más abajo

>> E=x(:,2).^2/2+5169.3034*(R0./(x(:,1).^2*2)-1./x(:,1)+x(:,1).^2*k/(2*RT^3))
E =
 -291.0826
 -291.0826
 -291.0826
 .....

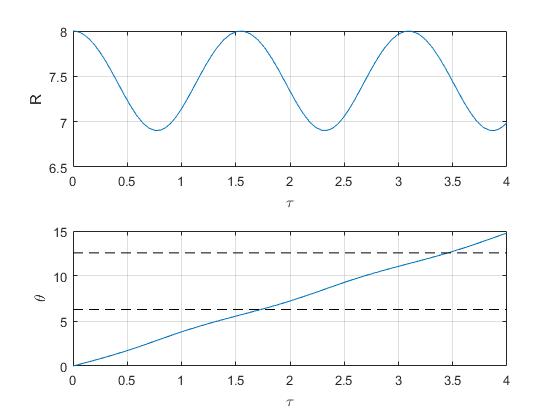
Representamos en la parte superior de la figura, la distancia radial R en función del tiempo τ. El periodo radial P_r, es el intervalo de tiempo entre dos máximos o dos mínimos

Representamos en la parte inferior de la figura, la posición angular θ en función del tiempo τ. El periodo P_θ, es el tiempo que tarda la posición angular en incrementarse 2π radianes. La primera línea a trazos marca la posición 2π, la segunda 4π, el periodo es el intervalo de tiempo entre dos intersecciones consecutivas

Energía

La suma de la energía cinética y potencial es

${\displaystyle \begin{array}{l}E=\frac{1}{2}m\left\{{\left(\frac{dr}{dt}\right)}^2+r^2{\left(\frac{d\theta }{dt}\right)}^2\right\}-G\frac{Mm}{r}+\frac{1}{2}\left(\frac{4}{3}\pi Gm\rho \right)r^2\\ E=\frac{1}{2}m{\left(\frac{dr}{dt}\right)}^2+\frac{L^2}{2m{r}^2}-G\frac{Mm}{r}+\frac{1}{2}GMmk\frac{r^2}{r_T^3}\end{array}}$

Sabiendo que el momento angular $L=m\sqrt{GM{r}_0}$, la energía E/m se escribe

${\displaystyle \frac{E}{m}=\frac{1}{2}{\left(\frac{dr}{dt}\right)}^2+\frac{GM{r}_0}{2r^2}-G\frac{M}{r}+\frac{1}{2}GMk\frac{r^2}{r_T^3}}$

En el sistema de unidades que hemos establecido,

${\displaystyle \frac{E}{m}\frac{{3600}^2}{{10}^{12}}=\frac{1}{2}{\left(\frac{dR}{d\tau }\right)}^2+5169.3\left(\frac{1}{2}\frac{R_0}{R^2}-\frac{1}{R}+\frac{1}{2}k\frac{R^2}{R_T^3}\right)}$

Energía potencial efectiva

Cuando se estudia el movimiento en la dirección radial, la energía potencial efectiva es

${\displaystyle E_{ef}=\frac{L^2}{2m{r}^2}-G\frac{Mm}{r}+\frac{1}{2}GMmk\frac{r^2}{r_T^3}}$

Con las condiciones iniciales especificadas, t=0, r=r₀ y dr/dt=0, $L=m\sqrt{GM{r}_0}$, la energía potencial efectiva es

${\displaystyle \begin{array}{l}\frac{E_{ef}}{GMm}=\frac{r_0}{2r^2}-\frac{1}{r}+\frac{1}{2}k\frac{r^2}{r_T^3}\\ e_{ef}=\frac{R_0}{2R^2}-\frac{1}{R}+\frac{1}{2}k\frac{R^2}{R_T^3}\end{array}}$

En la segunda fila expresamos la energía potencial efectiva en el sistema de unidades que hemos establecido

La energía es constante e igual a su valor en el instante inicial t=0, r=r₀ y dr/dt=0

${\displaystyle \begin{array}{l}\frac{E}{GMm}=-\frac{1}{2r_0}+\frac{1}{2}k\frac{r_0^2}{r_T^3}\\ e=-\frac{1}{2R_0}+\frac{1}{2}k\frac{R_0^2}{R_T^3}\end{array}}$

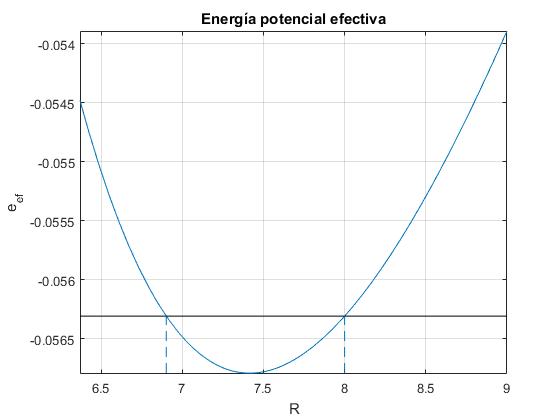
Representamos, la energía potencial efectiva e_ef, y superponemos la energía total e mediante una línea horizontal. Los puntos de intersección señalan las distancias R máxima y mínima del satélite al centro de fuerzas. Son las raíces reales de un polinomio de cuarto orden. Utilizamos la función roots de MATLAB para calcularlas y representarlas mediante líneas a trazos.

${\displaystyle \frac{k}{2R_T^3}{R}^4-e{R}^2-R+\frac{R_0}{2}=0}$

La energía potencial efectiva tiene un mínimo, que se obtiene derivando e_ef respecto de R e igualando a cero

${\displaystyle -\frac{k}{R_T^3}{R}^4+R+R_0=0}$

Utilizamos la función roots de MATLAB para calcular la raíz real positiva.

RT=6.37; %radio de la Tierra
R0=8; %Posición inicial del satálite 
k=0.05;
f=@(R) R0./(2*R.^2)-1./R+k*R.^2/(2*RT^3);
fplot(f,[RT,R0+1])
line([RT,R0+1],[f(R0),f(R0)],'color','k')
raices=roots([k/(2*RT^3),0,-f(R0),-1,R0/2])
raiz=zeros(2,1);
j=1;
for i=1:length(raices)
    if isreal(raices(i))
       raiz(j)=raices(i);
       j=j+1;
    end
end
%mínimo
raices=roots([k/RT^3,0,0,1,-R0]);
for i=1:length(raices)
    if isreal(raices(i)) & raices(i)>0
       Rmin=raices(i);
    end
end
for j=1:2
    line([raiz(j),raiz(j)],[f(Rmin), f(R0)],'lineStyle','--')
end
grid on
xlabel('R')
ylabel('e_{ef}')
title('Energía potencial efectiva')

Aproximación para órbitas casi circulares.

Partimos de la ecuación diferencial en la dirección radial. Hacemos que r=r₀+ξ,

${\displaystyle \begin{array}{l}\frac{d^{2}r}{d{t}^2}=\frac{L^2}{m^2{r}^3}-GM\frac{1}{r^2}-\frac{4}{3}\pi G\rho r\\ \frac{d^2\xi }{d{t}^2}=\frac{L^2}{m^2{r}_0^3{\left(1+\xi /r_0\right)}^3}-GM\frac{1}{r_0^2{\left(1+\xi /r_0\right)}^2}-\frac{4}{3}\pi G\rho r_0\left(1+\frac{\xi }{r_0}\right)\end{array}}$

Suponiendo que ξ/r₀<<1, hacemos la aproximación

${\displaystyle \begin{array}{l}{\left(1+\frac{\xi }{r_0}\right)}^{-3}\approx 1-3\frac{\xi }{r_0}\\ {\left(1+\frac{\xi }{r_0}\right)}^{-2}\approx 1-2\frac{\xi }{r_0}\end{array}}$

La ecuación diferencial se escribe

${\displaystyle \frac{d^2\xi }{d{t}^2}\approx \frac{L^2}{m^2{r}_0^3}\left(1-3\frac{\xi }{r_0}\right)-GM\frac{1}{r_0^2}\left(1-2\frac{\xi }{r_0}\right)-\frac{4}{3}\pi G\rho r_0\left(1+\frac{\xi }{r_0}\right)}$

Si r₀ es el radio de la órbita circular, d²r/dt²=0

${\displaystyle \frac{L^2}{m^2{r}_0^3}-GM\frac{1}{r_0^2}-\frac{4}{3}\pi G\rho r_0=0}$

obtenemos una ecuación diferencial sencilla

${\displaystyle \begin{array}{l}\frac{d^2\xi }{d{t}^2}+\left(3\frac{L^2}{m^2{r}_0^4}-2GM\frac{1}{r_0^3}+\frac{4}{3}\pi G\rho \right)\xi =0\\ \frac{d^2\xi }{d{t}^2}+\left\{\frac{L^2}{m^2{r}_0^4}+\frac{4}{3}\pi G\rho +\frac{2}{r_0}\left(\frac{L^2}{m^2{r}_0^3}-GM\frac{1}{r_0^2}\right)\right\}\xi =0\\ \frac{d^2\xi }{d{t}^2}+\left(\frac{L^2}{m^2{r}_0^4}+3GMk\frac{1}{r_T^3}\right)\xi =0\end{array}}$

Que es la ecuación diferencial de un Movimiento Armónico Simple. La frecuencia angular de la oscilación radial es,

${\displaystyle {\omega }_r=\sqrt{\frac{L^2}{m^2{r}_0^4}+3GMk\frac{1}{r_T^3}}}$

y el periodo P_r=2π/ω_r

Para $L=m\sqrt{GM{r}_0}$, densidad relativa k=0.05, r₀=8·10⁶ m y r_T=6.37·10⁶ m, obtenemos P_r=1.7362 h. La distancia entre dos mímimos de R en la gráfica es aproximadamente 1.6 h

El tiempo P_θ que tarda en dar una vuelta completa,

${\displaystyle {\omega }_{\theta }=\frac{d\theta }{dt}=\frac{L}{m{r}_0^2}}$

P_θ=2π/ω_θ

Con los datos anteriores, P_θ=1.9774 h

Ambos periodos P_r y P_θ son distintos, lo que da lugar a la precesión de la órbita

Referencias

Lim Yung-kuo. Problems and Solutions on Mechanics. World Scientific (1994). Problem 1047, pp. 66-69