Vamos a estudiar la trayectoria de una partícula de masa m que se mueve en el interior cuerpo de masa M de forma esférica de radio R cuya densidad es constante o bien, bajo la acción de una fuerza atractiva proporcional a la distancia r al centro fijo de fuerzas. Supondremos que el cuerpo permanece aislado en el espacio en reposo

Vamos a seguir los mismos pasos que en la página titulada Ecuación de la trayectoria para determinar la ecuación de la trayectoria de la partícula que supondremos que se mueve libremente en el interior del cuerpo bajo la fuerza de atracción F

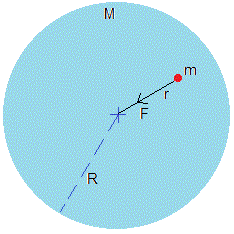
En la página titulada, La aceleración de la gravedad en el interior y en el exterior de una distribución esférica y uniforme de masa, demostramos que la fuerza de atracción es proporcional a la distancia r entre la partícula y el centro de la esfera.

${\displaystyle \overrightarrow{F}=-G\frac{Mm}{R^3}\overrightarrow{r}}$

Se trata de una fuerza conservativa cuya energía potencial vale

${\displaystyle E_p(r)=-\frac{3}{2}\frac{GMm}{R}+\frac{GMm}{R^3}\frac{r^2}{2}}$

El nivel cero de energía potencial se ha tomado en r=∞.

Ecuación de la trayectoria en coordenadas polares

Partimos de las expresiones:

• de la energía en coordenadas polares

${\displaystyle \begin{array}{l}E=\frac{1}{2}m{\left(\frac{dr}{dt}\right)}^2+\frac{1}{2}m{r}^2{\left(\frac{d\theta }{dt}\right)}^2-\frac{3}{2}\frac{GMm}{R}+\frac{GMm}{R^3}\frac{r^2}{2}\\ E^{\text{'}}=\frac{1}{2}m{\left(\frac{dr}{dt}\right)}^2+\frac{1}{2}m{r}^2{\left(\frac{d\theta }{dt}\right)}^2+\frac{GMm}{R^3}\frac{r^2}{2}\end{array}}$

• y del momento angular en coordenadas polares

${\displaystyle L=m{r}^2\frac{d\theta }{dt}}$

Despejamos dθ/dt en la expresión del momento angular y la introducimos en la expresión de la energía. Tenemos dos ecuaciones

${\displaystyle \begin{array}{l}{E}^{\text{'}}=\frac{1}{2}m{\left(\frac{dr}{dt}\right)}^2+\frac{L^2}{2m{r}^2}+\frac{GMm}{R^3}\frac{r^2}{2}\\ L=m{r}^2\frac{d\theta }{dt}\end{array}}$

Movimiento en la dirección radial

Analizamos la primera ecuación de la energía. Decimos que la partícula se mueve en una región unidimensional r>0 bajo un potencial efectivo, cuyo aspecto se muestra en la figura

${\displaystyle E_p(r)=\frac{L^2}{2m{r}^2}+\frac{GMm}{R^3}\frac{r^2}{2}}$

Representamos una función de la forma f(r)=a/r²+br² con a=1 y b=2. Calculamos los puntos de intersección con la recta horizontal e'=6

a=1; 
b=2; 
e=6; %energía
f=@(r) a./r.^2+b*r.^2;
fplot(f,[0.2,3],'color','r')
line([0,3],[e,e],'color','k')

%raíces
r1=(e+sqrt(e^2-4*a*b))/(2*b);
r2=(e-sqrt(e^2-4*a*b))/(2*b);
line([sqrt(r1),sqrt(r1)],[0,e], 'lineStyle','--')
line([sqrt(r2),sqrt(r2)],[0,e], 'lineStyle','--')
grid on
xlabel('r')
ylabel('V(r)')
title('Energía potencial')

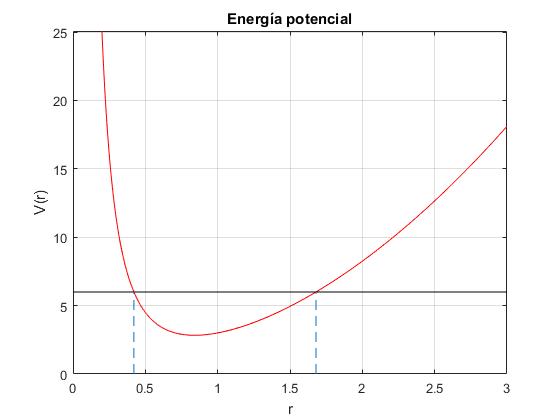
La energía E' tiene que ser mayor que el mínimo de la energía potencial efectiva. El valor mínimo de obtiene derivando E_p(r) respecto a r e igualando a cero

${\displaystyle \begin{array}{l}-\frac{L^2}{m{r}^3}+\frac{GMm}{R^3}r=0r_c={\left(\frac{L^2{R}^3}{GM{m}^2}\right)}^{1/4}\\ E_p{\left(r\right)}_{mín}=\frac{L}{R}\sqrt{\frac{GM}{R}}\end{array}}$

En el mínimo, el cuerpo describe una trayectoria circular de radio r_c con velocidad v_c. El momento angular L=mr_cv_c.

${\displaystyle v_c=\sqrt{\frac{GM}{R^3}{r}_c}}$

La misma expresión, se deduciría a partir de la dinámica del movimiento circular uniforme.

Cuando la energía total E' es mayor que el mínimo, como vemos en la gráfica, la recta horizontal que señala la energía total, corta a curva que describe la energía potencial E_p(r), en dos puntos r₁ y r₂, soluciones de la ecuación bicuadrada

${\displaystyle \begin{array}{l}{E}^{\text{'}}=\frac{L^2}{2m{r}^2}+\frac{GMm}{R^3}\frac{r^2}{2}\\ \frac{GMm}{2R^3}{r}^4-E^{\text{'}}{r}^2+\frac{L^2}{2m}=0\end{array}}$

Fuerza central y conservativa

Utilizamos las propiedades de la fuerza de atracción: central y conservativa, para obtener la ecuación de la trayectoria. Eliminamos el tiempo t sustituyendo dr/dt por

${\displaystyle \frac{dr}{dt}=\frac{dr}{d\theta }\frac{d\theta }{dt}=\frac{dr}{d\theta }\frac{L}{m{r}^2}}$

Despejamos dθ/dr en la ecuación de la energía

${\displaystyle d\theta =\frac{L}{\sqrt{2m}}\frac{dr/r^2}{\sqrt{\left(E^{\text{'}}-\frac{L^2}{2m{r}^2}-\frac{GMm}{2R^3}{r}^2\right)}}}$

Denominamos u=1/r

${\displaystyle d\theta =\frac{L}{\sqrt{2m}}\frac{-udu}{\sqrt{\left(E^{\text{'}}{u}^2-\frac{L^2}{2m}{u}^4-\frac{GMm}{2R^3}\right)}}}$

Teniendo en cuenta que u·du=du²/2, y llamando z=u²

${\displaystyle d\theta =\frac{1}{2}\frac{L}{\sqrt{2m}}\frac{-dz}{\sqrt{\left(E^{\text{'}}z-\frac{L^2}{2m}{z}^2-\frac{GMm}{2R^3}\right)}}}$

Resolvemos la integral

${\displaystyle \begin{array}{l}\theta -{\theta }_0=\frac{1}{2}\frac{L}{\sqrt{2m}}{\displaystyle \int \frac{-dz}{\sqrt{\left(-a{z}^2+bz-c\right)}}}\\ a=\frac{L^2}{2m}b=E\text{'}c=\frac{GMm}{2R^3}\end{array}}$

Donde θ₀ es la constante de integración que se determina a partir de las condiciones iniciales. Tenemos una integral del tipo

${\displaystyle {\displaystyle \int \frac{-dz}{\sqrt{a\left[\left(\frac{b^2}{4a^2}-\frac{c}{a}\right)-{\left(z-\frac{b}{2a}\right)}^2\right]}}}}$

Hacemos un nuevo cambio de variable

${\displaystyle z-\frac{b}{2a}=\sqrt{\frac{b^2}{4a^2}-\frac{c}{a}}\cos \xi }$

Con este cambio, la integral es inmediata

${\displaystyle \begin{array}{l}\theta -{\theta }_0=\frac{1}{2}\frac{L}{\sqrt{2m}}\frac{1}{\sqrt{a}}{{\displaystyle \int }}^{\text{}}d\xi \hfill \\ 2\left(\theta -{\theta }_0\right)=\xi \hfill \end{array}}$

Deshacemos los cambios

${\displaystyle \begin{array}{l}\begin{array}{l}z-\frac{b}{2a}=\sqrt{\frac{b^2}{4a^2}-\frac{c}{a}}\cos \left(2(\theta -{\theta }_0)\right)\hfill \\ u^2-\frac{b}{2a}=\sqrt{\frac{b^2}{4a^2}-\frac{c}{a}}\cos \left(2(\theta -{\theta }_0)\right)\hfill \\ \frac{1}{r^2}-\frac{mE\text{'}}{L^2}=\frac{m}{L}\sqrt{\frac{E{\text{'}}^2}{L^2}-\frac{GM}{R^3}}\cos \left(2(\theta -{\theta }_0)\right)\hfill \end{array}\hfill \\ \frac{1}{r^2}=\frac{mE\text{'}}{L^2}\left(1+\sqrt{1-\frac{GM{L}^2}{R^{3}E{\text{'}}^2}}\cos \left(2(\theta -{\theta }_0)\right)\right)\hfill \end{array}}$

La ecuación de la trayectoria en coordenadas polares es

${\displaystyle r^2=\frac{d}{1+\epsilon \cos \left(2(\theta -{\theta }_0)\right)}\epsilon =\sqrt{1-\frac{GM{L}^2}{R^{3}E{\text{'}}^2}}d=\frac{L^2}{mE\text{'}}}$

Periodo

Integramos la ecuación de la constancia del momento angular expresado en coordenadas polares

${\displaystyle \begin{array}{l}L=m{r}^2\frac{d\theta }{dt}\\ \underset{0}{\overset{2\pi }{{\displaystyle \int }}}{r}^{2}d\theta =\underset{0}{\overset{P}{{\displaystyle \int }}}\frac{L}{m}dt\\ \underset{0}{\overset{2\pi }{{\displaystyle \int }}}\frac{d}{1+\epsilon \cos \left(2\theta \right)}d\theta =\frac{L}{m}P\end{array}}$

La función cos(2θ) es peródica de periodo π, es positiva entre 0 y π/2 y negativa de π/2 a π. El primer miembro se puede expresar como la suma

${\displaystyle \begin{array}{l}d\underset{0}{\overset{2\pi }{{\displaystyle \int }}}\frac{d\theta }{1+\epsilon \cos \left(2\theta \right)}=2d\underset{0}{\overset{\pi }{{\displaystyle \int }}}\frac{d\theta }{1+\epsilon \cos \left(2\theta \right)}=\\ 2d\left\{\underset{0}{\overset{\pi /2}{{\displaystyle \int }}}\frac{d\theta }{1+\epsilon \cos \left(2\theta \right)}+\underset{0}{\overset{\pi /2}{{\displaystyle \int }}}\frac{d\theta }{1-\epsilon \cos \left(2\theta \right)}\right\}\end{array}}$

Las integrales son del tipo

${\displaystyle \underset{0}{\overset{\pi /2}{{\displaystyle \int }}}\frac{dx}{1+a\cos \left(2x\right)}}$

con a=±ε, con ε<1. Hacemos el cambio de variable

${\displaystyle t=\tan xdt=\frac{1}{{\cos }^{2}x}dx}$

Los límites de integración de t son 0 e ∞. Con las relaciones

${\displaystyle \begin{array}{l}\frac{1}{{\cos }^{2}x}=1+t^2{\sin }^{2}x=\frac{t^2}{1+t^2}\\ \cos (2x)={\cos }^{2}x-{\sin }^{2}x=\frac{1-t^2}{1+t^2}\end{array}}$

La integral se resuelve

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{dt}{(1-a)t^2+(1+a)}}=\frac{1}{1-a}{\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{dt}{t^2+{\left(\sqrt{\frac{1+a}{1-a}}\right)}^2}}={\frac{1}{\sqrt{1-a^2}}\arctan \left(\sqrt{\frac{1-a}{1+a}}t\right)|}_0^{\infty }\\ =\frac{\pi }{2\sqrt{1-a^2}}\end{array}}$

El primer miembro vale

${\displaystyle d\underset{0}{\overset{2\pi }{{\displaystyle \int }}}\frac{d\theta }{1+\epsilon \cos \left(2\theta \right)}=2d\left\{\frac{\pi }{2\sqrt{1-{\epsilon }^2}}+\frac{\pi }{2\sqrt{1-{\epsilon }^2}}\right\}=\frac{2\pi d}{\sqrt{1-{\epsilon }^2}}}$

Sustituyendo los parámetros d y ε por sus expresiones en términos de la energía E' y momento angular L, simplificando

${\displaystyle \begin{array}{l}\frac{2\pi d}{\sqrt{1-{\epsilon }^2}}=\frac{L}{m}P\\ P=\frac{2\pi }{\sqrt{\frac{GM}{R^3}}}=\frac{2\pi }{\omega }\end{array}}$

Ecuación del movimiento

Vamos a ver que es mucho más sencillo integrar directamente la ecuación del movimiento

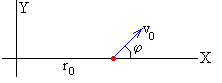
Vamos a determinar la ecuación de la trayectoria de una partícula de masa m bajo la acción de una fuerza central atractiva, proporcional a la distancia al centro fijo de fuerzas. La partícula parte de la posición (r₀, 0) con velocidad v₀ haciendo un ángulo φ con el eje X, tal como se muestra en la figura.

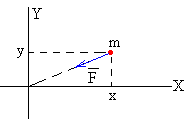
Cuando la partícula se encuentra en la posición $\overrightarrow{r}=x\widehat{i}+y\widehat{j}$ , la fuerza que actúa sobre la partícula es $-k\overrightarrow{r}=-kx\widehat{i}-ky\widehat{j}$

con k=GMm/R³. La ecuación del movimiento de la partícula es:

${\displaystyle m\frac{d^2\overrightarrow{r}}{d{t}^2}=-k\overrightarrow{r}\begin{array}{l}\frac{d^{2}x}{d{t}^2}+{\omega }^{2}x=0\\ \frac{d^{2}y}{d{t}^2}+{\omega }^{2}y=0\end{array}\}\omega =\sqrt{\frac{k}{m}}}$

La solución de este sistema de dos ecuaciones diferenciales es:

${\displaystyle \begin{array}{l}x=A_x\sin (\omega t)+B_x\cos (\omega t)\\ y=A_y\sin (\omega t)+B_y\cos (\omega t)\end{array}\}\omega =\sqrt{\frac{GM}{R^3}}}$

Que es la composición de dos MAS de la misma frecuencia y direcciones perpendiculares

El periodo o tiempo que tarda en completar una vuelta es P=2π/ω, tal como hemos obtenido en la sección anterior

Las componentes de la velocidad de la partícula son

${\displaystyle \begin{array}{l}\frac{dx}{dt}=\omega \left(A_x\cos \left(\omega t\right)-B_x\sin \left(\omega t\right)\right)\\ \frac{dy}{dt}=\omega \left(A_y\cos \left(\omega t\right)-B_y\sin \left(\omega t\right)\right)\end{array}}$

Las constantes A_x, A_y, B_x y B_y se determinan a partir de las condiciones iniciales, en el instante t=0, la partícula parte de la posición x=r₀, y=0, con velocidad v_x=v₀·cosφ, v_y=v₀·sinφ.

${\displaystyle \begin{array}{l}{B}_x=r_0{B}_y=0\\ A_x=\frac{v_0\cos \phi }{\omega }{A}_y=\frac{v_0\sin \phi }{\omega }\end{array}}$

Las coordenadas x e y de la partícula son:

${\displaystyle \begin{array}{l}x=\frac{v_0\cos \phi }{\omega }\sin \left(\omega t\right)+r_0\cos \left(\omega t\right)\\ y=\frac{v_0\sin \phi }{\omega }\sin \left(\omega t\right)\end{array}}$

Eliminando el tiempo t obtenemos la ecuación de la trayectoria

${\displaystyle x^2+\left(\frac{v_0^2{\cos }^2\phi +{\omega }^2{r}_0^2}{v_0^2{\sin }^2\phi }\right)y^2-2xy\frac{1}{\tan \phi }=r_0^2}$

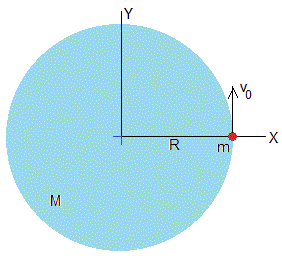
El ejemplo más sencillo se produce cuando φ=90°, y r₀=R. La partícula se lanza desde la superficie de la Tierra con velocidad tangencial v₀

La ecuación de la trayectoria es

${\displaystyle \{\begin{array}{l}x=R\cos (\omega t)\\ y=\frac{v_0}{\omega }\sin (\omega t)\end{array}}$

Cuando ωt=π/2, la partícula dista del origen v₀/ω, es el máximo acercamiento

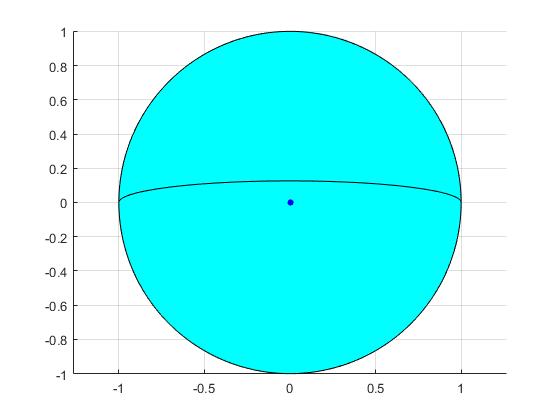
R=6371*1000; %radio de la Tierra
M=5.972e24; %masa de la Tierra
G=6.674e-11; %constante G

r0=R;
hold on
ang=(1:360)*pi/180;
fill(cos(ang),sin(ang),'c') %la Tierra
plot (0,0,'o','markersize',4,'markeredgecolor','b','markerfacecolor','b')
%trayectoria en el interior de la Tierra
v0=1000;
vx=0;
vy=v0;
w=sqrt(G*M/R^3);
Ax=0; Ay=vy/w;
Bx=r0; By=0;
fplot(@(t) (Ax*sin(w*t)+Bx*cos(w*t))/R, @(t) (Ay*sin(w*t)+By*cos(w*t))/R,[0,pi/w],'k')
grid on
hold off
axis equal

>> v0/w
ans =   8.0549e+05

La energía E' y el momento angular L son, respectivamente

${\displaystyle \begin{array}{l}{E}^{\text{'}}=\frac{1}{2}m{v}_0^2+\frac{GMm}{2R^3}{R}^2=\frac{1}{2}m{v}_0^2+\frac{GMm}{2R}\\ L=mR{v}_0\end{array}}$

La ecuación de la trayectoria es

${\displaystyle r^2=\frac{d}{1+\epsilon \cos \left(2(\theta -{\theta }_0)\right)}}$

Con el siguiente código obtenemos la misma trayectoria

R=6371*1000; %radio de la Tierra
M=5.972e24; %masa de la Tierra
G=6.674e-11; %constante G

r0=R; %desde el centro de la Tierra
hold on
ang=(1:360)*pi/180;
fill(cos(ang),sin(ang),'c') %la Tierra
plot (0,0,'o','markersize',4,'markeredgecolor','b','markerfacecolor','b')
%trayectoria en el interior de la Tierra
v0=1000;
Ep=v0^2/2+G*M/(2*R);
epsilon=sqrt(1-G*M*(r0*v0)^2/(R^3*Ep^2));
d=(r0*v0)^2/Ep;
ang=(0:180)*pi/180;
r2=@(x) d./(1+epsilon*cos(2*x-pi));
plot(sqrt(r2(ang)).*cos(ang)/R, sqrt(r2(ang)).*sin(ang)/R,'k')
grid on
hold off
axis equal

La distancia más próxima al centro de la Tierra se produce cuando θ=π/2

>> sqrt(r2(pi/2))
ans =   8.0549e+05

La envolvente

La ecuación de la trayectoria depende del ángulo φ con el que se dispara la partícula.

f(x, y, φ)=0

La ecuación de la envolvente de las trayectorias se obtiene derivando con respecto a φ e igualando a cero.

${\displaystyle \begin{array}{l}\frac{\partial f}{\partial \phi }=0\\ -\frac{2\cos \phi \left(r_0^2{\omega }^2+v_0^2\right)}{v_0^2{\sin }^3\phi }{y}^2+2xy\frac{1}{{\sin }^2\phi }=0\\ \tan \phi =\frac{y}{x}\frac{\left({\omega }^2{r}_0^2+v_0^2\right)}{v_0^2}\end{array}}$

y combinando ésta con la ecuación de la trayectoria para eliminar el ángulo φ. Para ello, empleamos las relaciones trigonométricas

${\displaystyle \begin{array}{l}{\cos }^2\phi =\frac{1}{1+{\tan }^2\phi }=\frac{v_0^4{x}^2}{v_0^4{x}^2+{\left({\omega }^2{r}_0^2+v_0^2\right)}^2{y}^2}\\ {\sin }^2\phi =\frac{{\tan }^2\phi }{1+{\tan }^2\phi }=\frac{{\left({\omega }^2{r}_0^2+v_0^2\right)}^2{y}^2}{v_0^4{x}^2+{\left({\omega }^2{r}_0^2+v_0^2\right)}^2{y}^2}\end{array}}$

Introducimos las expresiones de sin²φ, cos²φ y tanφ en la ecuación de la trayectoria obteniendo la ecuación de la envolvente, que es una elipse de semiejes a y b.

${\displaystyle \begin{array}{l}\frac{{\omega }^2}{v_0^2+{\omega }^2{r}_0^2}{x}^2+\frac{{\omega }^2}{v_0^2}{y}^2=1\\ a=\sqrt{r_0^2+\frac{v_0^2}{{\omega }^2}}b=\frac{v_0}{\omega }\end{array}}$

Actividades

Se introduce

• La posición r₀ de disparo de la partícula, en el control titulado Posición.
• La velocidad de disparo v₀, en el control titulado Velocidad.
• Se ha fijado la frecuencia angular ω=1

Se pulsa el botón titulado Nuevo

Se observa las trayectorias de las partículas disparadas con ángulos φ=0º, 30º, 60º, 90º, 120º, 150º, 180º, 210º, 240º, 270º, 300º, 330º y la envolvente de todas las trayectorias elípticas.

Referencias

French A. P. The envelopes of some families of fixed-energy trajectories. Am. J. Phys. 61 (9) September 1993