Choque de un meteorito con la Tierra inmóvil

Primero, vamos a resolver un problema sencillo que se plantea habitualmente en un curso de Física General:

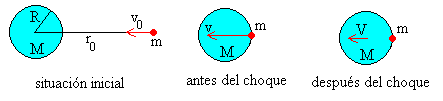
Supongamos la Tierra de masa M y radio R inmóvil en el espacio, un meteorito de masa m<<M se mueve en la dirección radial hacia el centro de la Tierra con velocidad v₀ cuando está a una distancia r₀>R. Determinar

• La velocidad v del meteorito justamente antes del impacto.
• La velocidad V del conjunto después del choque inelástico entre la Tierra y el meteorito.

Para resolver el problema supondremos que la masa m del meteorito es pequeña comparada con la masa M de la Tierra, es decir, la fuerza de atracción del meteorito sobre la Tierra no causa un movimiento apreciable de ésta.

La fuerza de atracción es conservativa, por lo que la energía total del meteorito permanece constante.

${\displaystyle \frac{1}{2}m{v}_0^2-\frac{GMm}{r_0}=\frac{1}{2}m{v}^2-\frac{GMm}{R}}$

Los datos son v₀ y r₀ y la incógnita es la velocidad v del meteorito justamente antes del choque con la Tierra.

La Tierra y el meteorito forman un sistema aislado, aplicando el principio de conservación del momento lineal,

m·v=(m+M)V

obtenemos la velocidad del conjunto Tierra-meteorito después del choque. Parte de la energía cinética del meteorito que se ha trasformado en energía interna del conjunto.

${\displaystyle Q=\frac{1}{2}m{v}^2-\frac{1}{2}(m+M)V^2}$

Ejemplo

Un meteorito de m=2·10⁷ kg de masa se dirige desde el espacio exterior hacia la Tierra. Su velocidad a una distancia de r₀=3.8·10⁷ m del centro de la Tierra es v₀=30 km/s. Calcular:

• La velocidad con la que llega a la superficie de la Tierra (se supone que la Tierra permanece inmóvil antes del choque)

• La velocidad del conjunto Tierra-meteorito después del choque

• La energía cinética del meteorito transformada en energía interna del sistema.

Datos:

• Masa de la Tierra, M=5.98·10²⁴ kg
• Radio de la Tierra, R=6.37·10⁶ m
• Constante, G=6.67·10^-11 Nm²/kg²

Resultados:

• La velocidad con que llega el meteorito a la superficie de la Tierra, v=31689.7 m/s, su energía cinética es E_k=1.0·10¹⁶ J

• Velocidad del conjunto después del choque, V=1.06·10^-13 m/s

• Energía cinética transformada en energía interna es Q=1.0·10¹⁶ J.

Prácticamente, toda la energía cinética del meteorito se transforma en energía interna, el centro de masas de la Tierra apenas se ve afectado por el choque, su velocidad no cambia apreciablemente.

Choque de un meteorito con la Tierra en órbita circular alrededor del Sol

Orbita circular de la Tierra

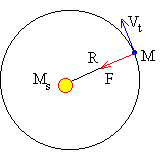
Supondremos que la Tierra describe un órbita circular de radio R=1.49·10¹¹ m alrededor del Sol. Aplicando la ecuación de la dinámica del movimiento circular uniforme, obtenemos la velocidad constante V_t de la Tierra en su movimiento de traslación alrededor del Sol.

${\displaystyle M\frac{V_t^2}{R}=\frac{G{M}_{s}M}{R^2}{V}_t=\sqrt{\frac{G{M}_s}{R}}}$

Los datos que se precisan son:

• El radio de la órbita circular de la Tierra, R=1.49·10¹¹ m.

• La masa del Sol M_s=1.98·10³⁰ kg

El resultado es V_t=29771.6 m/s

El periodo de la Tierra o tiempo que tarda en dar una vuelta completa es

${\displaystyle P=\frac{2\pi R}{V_t}=2\pi \sqrt{\frac{R^3}{G{M}_s}}=363.96\text{ días}}$

Choque de un meteorito con la Tierra.

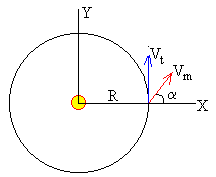
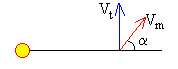
Establecemos un sistema inercial de referencia con origen en el Sol, la Tierra justamente antes del choque está situada en el eje X a una distancia R del Sol, y se mueve a lo largo del eje Y con velocidad V_t. El meteorito se mueve con velocidad V_m relativa al Sol haciendo un ángulo α con el eje X, tal como se indica en la figura. Aplicando el principio de conservación del momento lineal

${\displaystyle m\overrightarrow{V_m}+M\overrightarrow{V_t}=(m+M)\overrightarrow{v}}$

o bien,

mV_m·cosα=(m+M)v_x
mV_m·sinα+MV_t=(m+M)v_y

donde m es la masa del meteorito, M la masa de la Tierra, V_t la velocidad de traslación de la Tierra alrededor del Sol y v la velocidad del conjunto formado por la Tierra y el meteorito después del choque.

Calculamos el módulo de la velocidad v y su dirección φ después del choque.

${\displaystyle v=\frac{\sqrt{{\gamma }^2{V}_m^2+v_t^2+2\gamma V_m{V}_t\text{sin}\alpha }}{\text{1}+\gamma }\tan \phi =\frac{\gamma V_m·\text{sin}\alpha +V_t}{\gamma V_m\cos \alpha }}$

donde γ=m/M cociente entre la masas del meteorito y de la Tierra

Trayectoria del sistema formado por la Tierra y el meteorito

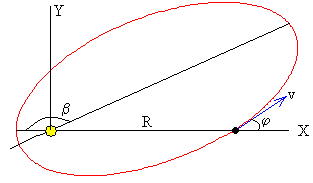
Calculamos la trayectoria seguida por una partícula de masa (m+M) bajo la fuerza de atracción del Sol, sabiendo que en el instante inicial está alejada una distancia R y lleva una velocidad v que hace un ángulo φ con el eje horizontal tal como se indica en la figura

Se trata de un problema similar al resuelto en la página titulada  “Trayectoria de un proyectil disparado desde una altura h por encima de la superficie terrestre”.

El momento angular y la energía de la combinación meteorito-Tierra después del choque es, respectivamente

${\displaystyle \begin{array}{l}L=(m+M)Rv·\text{sin}\phi \\ E=\frac{1}{2}(m+M)v^2-\frac{G{M}_s(M+m)}{R}\end{array}}$

La ecuación de la trayectoria en coordenadas polares es

${\displaystyle r=\frac{d}{1+\epsilon \cos \left(\theta -{\theta }_0\right)},\epsilon =\sqrt{1+\frac{2L^{2}E}{G^2{M}_s^2{(m+M)}^3}},d=\frac{L^2}{G{M}_s{(m+M)}^2}}$

La ecuación de la trayectoria es independiente de la masa de la partícula

Si la energía de la partícula es negativa E<0 su trayectoria es una elipse, y su excentricidad ε<1.

Conocido d y ε,  se calcula el semieje mayor a, que es la media aritmética de los radios mínimo (θ=0)  y máximo (θ=π) de la elipse.

${\displaystyle 2a=\frac{d}{1+\epsilon }+\frac{d}{1-\epsilon }}$

El periodo viene dado por la fórmula

${\displaystyle P^2=\frac{4{\pi }^2{a}^3}{GM}}$

Como vemos en la figura, la trayectoria que sigue la partícula es una elipse girada un ángulo β. Este ángulo se calcula poniendo r=R en la ecuación de la trayectoria y despejando el ángulo θ

${\displaystyle \cos \beta =\frac{1}{\epsilon }\left(\frac{d}{R}-1\right)}$

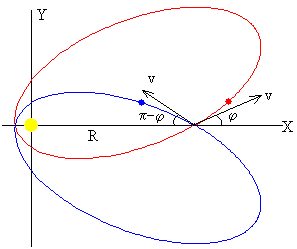
Las partículas cuyas direcciones iniciales formen con el eje X ángulos φ y 180-φ tienen la misma energía y el mismo momento angular, la trayectoria es una elipse con los mismos valores del parámetro d, y de la excentricidad ε, pero su orientación es distinta β, y 2π-β.

Las partículas cuyas direcciones iniciales formen con el eje X ángulos φ y π+φ describen la misma trayectoria pero en sentido opuestos.

Los meteoritos cuyas velocidades forman ángulos de 0º o de 180º con el eje X, al chocar con la Tierra producen trayectorias que tienen la misma excentricidad y el mismo periodo pero que tienen una orientación distinta, ya que las velocidades finales del conjunto formado por la Tierra y el meteorito después del choque forman ángulos suplementarios.

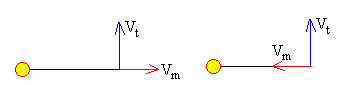
Los cambios más dramáticos se producen en un choque frontal entre el meteorito y la Tierra, es decir, cuando la dirección de la velocidad del meteorito forma 270º con el eje X.

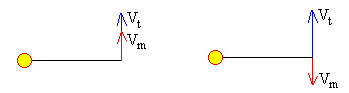
Como ejercicio numérico vamos a estudiar, dos ejemplos, un choque frontal y un choque oblicuo.

Trayectoria

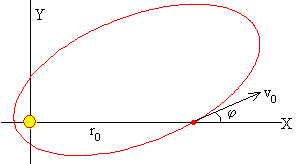
Para representar la trayectoria de un elipse girada es más conveniente utilizar esta ecuación

${\displaystyle \begin{array}{l}\frac{r_0}{r}=-\frac{\cos \phi }{\sin \phi }\sin \theta +\cos \theta +\frac{p(1-\cos \theta )}{2{\sin }^2\phi }\\ p=\frac{2GM}{r_0{v}_0^2}\end{array}}$

p es un parámetro adimensional

Choque frontal

• Sea γ=m/M=0.1 el cociente entre la masa del meteorito y la masa de la Tierra
• Velocidad del meteorito V_m=30000 m/s
• El ángulo que forma la dirección de la velocidad del meteorito con el eje X, α=270º

Planteamos las ecuaciones del choque inelástico a lo largo del eje Y

-γV_m +V_t=(γ+1)v

Conocida la velocidad V_t de la Tierra antes del choque, despejamos la velocidad final del conjunto después del choque v=24337.8 m/s a lo largo del eje Y, φ=90º.

Calculamos el momento angular y la energía en función de la masa m+M, ya que la ecuación de la órbita es independiente de la masa de la partícula. Se precisa el dato de la masa del Sol, M_s=1.98·10³⁰ kg y del radio de la órbita de la Tierra R=1.49·10¹¹ m

E=-590.2·10⁶ (m+M) J
L=3.63·10¹⁵ (m+M) kgm²/s

Con estos datos calculamos la excentricidad de la órbita ε y el parámetro d

d=0.996·10¹¹ m
ε=0.332

El semieje mayor de la elipse es a=1.19·10¹¹ m y el periodo P=236.83 días

vT=29771.6; %velocidad orbital de la Tierra, m/s
R=1.49e11; %radio de la órbita de la Tierra
gamma=0.1; %relación m/M entre masas 
alpha=3*pi/2;  %270°
vM=30000; %velocidad del meteorito
%componentes de la velocidad después del choque
vX=gamma*vM*cos(alpha)/(1+gamma);
vY=(gamma*vM*sin(alpha)+vT)/(1+gamma);
%momento angular y energía
L=R*vY;
E=(vX^2+vY^2)/2-6.67e-11*1.98e30/R;
ex=sqrt(1+2*L^2*E/(6.67e-11*1.98e30)^2); %excentricidad
d=L^2/(6.67e-11*1.98e30); %parámetro d de la elipse
a=d/(1-ex^2);  %semieje mayor
P=2*pi*sqrt(a^3/(6.67e-11*1.98e30))/(24*3600);  %periodo en días
fprintf('excentricidad %1.3f, periodo %3.1f\n',ex,P)

%trayectoria
v0=sqrt(vX^2+vY^2);
phi=atan2(vY,vX);
p=2*6.67e-11*1.98e30/(R*v0^2);
r0=1; %el radio de la Tierra se toma como unidad
r=@(x) r0./(-cos(phi)*sin(x)/sin(phi)+cos(x)+p*(1-cos(x))/(2*sin(phi)^2));
hold on
fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[0,2*pi])
%punto de lanzamiento
plot(r0,0,'ko', 'markersize',4,'markerfacecolor','k')
%vector velocidad inicial, en unidades de la velocidad de la Tierra
quiver(r0,0, v0*cos(phi)/vT, v0*sin(phi)/vT, 'color','k')
hold off
axis equal
xlabel('x')
ylabel('y')
grid on
title('Trayectoria elíptica')

La flecha indica la velocidad después del choque en unidades de la velocidad de la Tierra

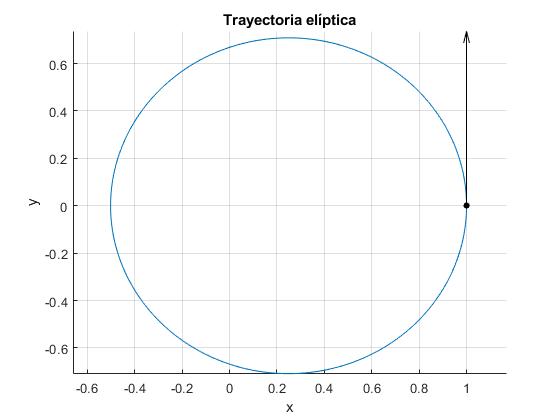
excentricidad 0.332, periodo 236.8

Choque oblicuo

Cambiamos el ángulo a α=60º y planteamos las ecuaciones de conservación del momento lineal a lo largo del eje X y a lo largo del eje Y.

γV_m·cosα=(γ+1)v_x
γV_m·sinα+V_t=(γ+1)v_y

Conocida la velocidad V_t de la Tierra antes del choque, despejamos la velocidad final del conjunto después del choque v=29458.6 m/s y su dirección, φ=87.3º.

Calculamos el momento angular y la energía

E=-452.4·10⁶ (m+M) J
L=4.38·10¹⁵ (m+M) kgm²/s

Con estos datos calculamos la excentricidad de la órbita ε y el parámetro d

d=1.456·10¹¹ m
ε=0.051

La trayectoria es una elipse cuyo eje mayor está girada un ángulo β=117º

El semieje mayor de la elipse es a=1.459·10¹¹ m y el periodo P=352.83 días

vT=29771.6; %velocidad orbital de la Tierra, m/s
R=1.49e11; %radio de la órbita de la Tierra
gamma=0.1; %relación m/M entre masas 
alpha=pi/3;  %60°
vM=30000; %velocidad del meteorito
%componentes de la velocidad después del choque
vX=gamma*vM*cos(alpha)/(1+gamma);
vY=(gamma*vM*sin(alpha)+vT)/(1+gamma);
%momento angular y energía
L=R*vY;
E=(vX^2+vY^2)/2-6.67e-11*1.98e30/R;
ex=sqrt(1+2*L^2*E/(6.67e-11*1.98e30)^2); %excentricidad
d=L^2/(6.67e-11*1.98e30); %parámetro d de la elipse
a=d/(1-ex^2);  %semieje mayor
P=2*pi*sqrt(a^3/(6.67e-11*1.98e30))/(24*3600);  %periodo en días
fprintf('excentricidad %1.3f, periodo %3.1f\n',ex,P)

%trayectoria
v0=sqrt(vX^2+vY^2);
phi=atan2(vY,vX);
p=2*6.67e-11*1.98e30/(R*v0^2);
r0=1; %el radio de la Tierra se toma como unidad
r=@(x) r0./(-cos(phi)*sin(x)/sin(phi)+cos(x)+p*(1-cos(x))/(2*sin(phi)^2));
hold on
fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[0,2*pi])
%punto de lanzamiento
plot(r0,0,'ko', 'markersize',4,'markerfacecolor','k')
%vector velocidad inicial, en unidades de la velocidad de la Tierra
quiver(r0,0, v0*cos(phi)/vT, v0*sin(phi)/vT, 'color','k')

%eje mayor de la elipse
th_0=-acos((d/R-r0)/(r0*ex));
x1=r(th_0)*cos(th_0);
y1=r(th_0)*sin(th_0);
x2=r(th_0+pi)*cos(th_0+pi);
y2=r(th_0+pi)*sin(th_0+pi);
line([x1,x2],[y1,y2])
hold off
axis equal
xlabel('x')
ylabel('y')
grid on
title('Trayectoria elíptica')

Se obtiene una trayectoria casi circular. Se muestra el eje mayor de la elipse girada

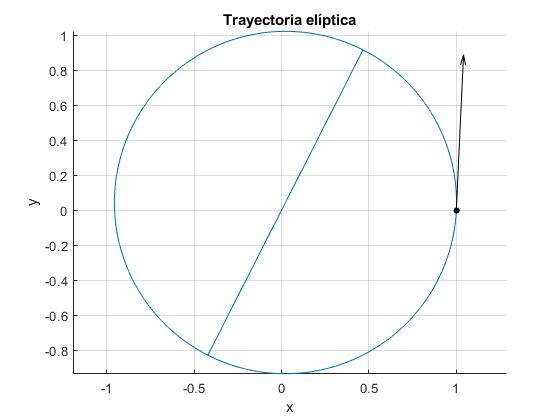
excentricidad 0.051, periodo 352.8

Variación de la excentricidad con el ángulo α

En la figura, se muestra el comportamiento complejo de la excentricidad ε en función del ángulo α que forma la dirección de la velocidad $\overrightarrow{V_m}$ del meteorito con el eje X para tres velocidades distintas del meteorito.

vT=29771.6; %velocidad orbital de la Tierra, m/s
R=1.49e11; %radio de la órbita circular de la Tierra
gamma=0.1; %relación m/M entre masas  

hold on
for vM=30000:30000:90000 %velocidad del meteorito
    alpha=(0:360)*pi/180;
    %componentes de la velocidad después del choque
    vX=gamma*vM*cos(alpha)/(1+gamma);
    vY=(gamma*vM*sin(alpha)+vT)/(1+gamma);
    %momento angular y energía
    L=R*vY;
    E=(vX.^2+vY.^2)/2-6.67e-11*1.98e30/R;
    ex=sqrt(1+2*L.^2.*E/(6.67e-11*1.98e30)^2); %excentricidad
    plot(alpha,ex,'displayName',num2str(vM))
end
hold off
legend('-DynamicLegend','location','northwest')
set(gca,'XTick',0:pi/2:2*pi)
set(gca,'XTickLabel',{'0','\pi/2','\pi','3\pi/2','2\pi'})
grid on
xlabel('\alpha')
ylabel('\epsilon')
title('Excentricidad de la órbita después del choque')

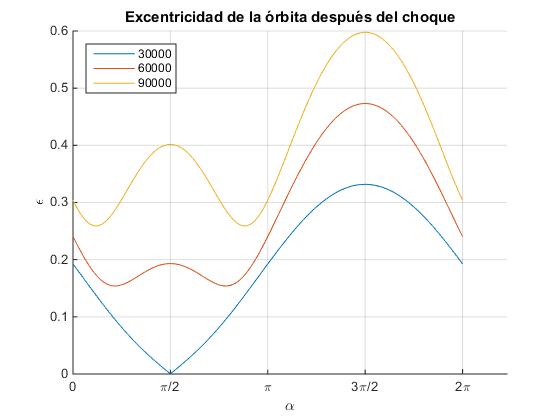
La excentricidad tiene un valor máximo para α=270º que es el choque frontal.

Para velocidades grandes del meteorito, hay mínimos para ciertos ángulos cuyo valor se obtiene en el artículo citado en las referencias.

Actividades

Se introduce

• El cociente γ=m/M entre la masa del meteorito y la masa de la Tierra (5.98·10²⁴ kg), en el control titulado Cociente masas.

• La velocidad del meteorito V_m en km/s en el control titulado Velocidad

• El ángulo α que forma la dirección de la velocidad del meteorito con el eje X,en el control titulado Angulo

Se pulsa el botón titulado Nuevo

Si como consecuencia del choque, la energía de la partícula resultante es positiva o nula, el programa no prosigue e invita al usuario a disminuir la velocidad del meteorito.

Se observa el movimiento rectilíneo del meteorito y circular de la Tierra antes del choque, que se produce en el eje horizontal X a una distancia R=1.49·10¹¹ m del Sol. Se observa la trayectoria del conjunto formado por la Tierra y el meteorito después de choque.

El programa interactivo proporciona los datos de la excentricidad y del periodo de la nueva órbita.

Referencias

Mohazzabi P., Luecke J. Asteroid impact and eccentricity of Earth’s orbit. Am. J. Phys. 71 (7) July 2003, pp. 687-690