En la página titulada Trayectoria de un proyectil disparado desde una altura h sobre la superficie de la Tierra, hemos estudiado las trayectorias de un proyectil disparado desde una altura h sobre la superficie de la Tierra con velocidad v₀ haciendo distintos ángulos φ con la dirección radial. En esta página, nos limitaremos al caso φ=90°, el disparo se produce en la dirección tangencial

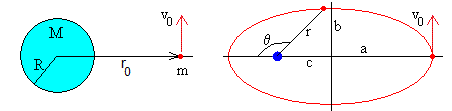
Se dispara un proyectil de masa m desde una distancia r₀=R+h del centro de la Tierra, con velocidad v₀ haciendo un ángulo 90° con el radio vector. El momento angular y la energía del proyectil son, respectivamente.

${\displaystyle \begin{array}{l}L=m{r}_0{v}_0\text{sin}90º=m{r}_0{v}_0\hfill \\ E=\frac{1}{2}m{v}_0^2-\frac{GMm}{r_0}\hfill \end{array}}$

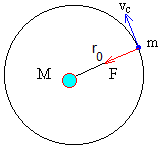
La ecuación de la dinámica del movimiento circular uniforme, nos proporciona la velocidad v_c de disparo del proyectil para que describa una órbita circular de radio r₀

${\displaystyle m\frac{v_c^2}{r_0}=\frac{GMm}{r_0}{v}_c=\sqrt{\frac{GM}{r_0}}}$

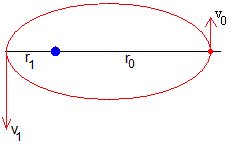
Conocidos r₀ y v₀, calculamos r₁ y v₁ a partir de la constancia del momento angular y la energía

${\displaystyle \begin{array}{l}\{\begin{array}{l}m{r}_0{v}_0=m{r}_1{v}_1\\ \frac{1}{2}m{v}_0^2-\frac{GmM}{r_0}=\frac{1}{2}m{v}_1^2-\frac{GmM}{r_1}\end{array}\\ r_1=\frac{r_0^2{v}_0^2}{2GM-r_0{v}_0^2}{v}_1=\frac{2GM}{r_0{v}_0}-v_0=\frac{2v_c^2}{v_0}-v_0\end{array}}$

• Si v₀>v_c, v₁<v₀ y r₁>r₀. La posición de disparo es el perigeo
• Si v₀<v_c, v₁>v₀ y r₁<r₀. La posición de disparo es el apogeo, tal como se muestra en la figura

Estamos interesados en los proyectiles que impacten sobre la superficie de la Tierra, aquellos en los que r₁<R y por tanto, la posición de disparo es el apogeo.

Por ejemplo, si el disparo se produce sobre el polo Norte, cuando r₁=R, el proyectil roza tangencialmente la superficie de la Tierra en el polo Sur. La velocidad de disparo para esta trayectoria elíptica vale

${\displaystyle \begin{array}{l}R=\frac{r_0^2{v}_m^2}{2GM-r_0{v}_m^2}\\ v_m=\sqrt{\frac{2GMR}{r_0\left(r_0+R\right)}}\end{array}}$

Para que impacte sobre la superficie de la Tierra el proyectil debería ser disparado con velocidad v₀<v_m

Ejemplos

Sea el radio de la Tierra, R=6371 km, la masa M=5.972·10²⁴ kg y G=6.674·10^-11 Nm²/kg².

Se dispara un proyectil desde una altura h=2700 km, por lo que r₀=9071 km.

• Para que el proyectil describa una trayectoria circular de radio r₀, la velocidad de disparo debería ser v_c= 6.6287 km/s.
• Para que el proyectil roce tangencialmente la Tierra su velocidad debería ser v_m=6.0213 km/s

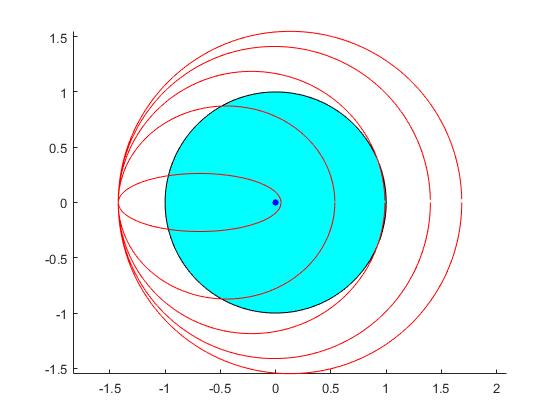
Dibujamos las trayectorias de los proyectiles disparados con velocidades v₀ crecientes desde la misma posición r₀.

R=6371*1000; %radio de la Tierra
M=5.972e24; %masa de la Tierra
G=6.674e-11; %constante G

h=2700*1000; %altura de disparo
r0=R+h; %desde el centro de la Tierra
hold on
ang=(1:360)*pi/180;
fill(cos(ang),sin(ang),'c') %la Tierra
%trayectorias 
for v0=[1.70,4.90,6.00,6.60,6.90]*1000; %velocidad de disparo
    d=r0^2*v0^2/(G*M); 
    e=sqrt(1+r0*v0^2*(r0*v0^2-2*G*M)/(G*M)^2);
    delta=0;
    if v0>6.6*1000
        delta=pi;
    end
    %trayectorias elípticas
    r=@(x) d./(1+e*cos(x+delta));
    plot(r(ang).*cos(ang)/R, r(ang).*sin(ang)/R, 'r')
end
%centro de la Tierra
plot (0,0,'o','markersize',4,'markeredgecolor','b','markerfacecolor','b')
hold off
axis equal

>> vc=sqrt(G*M/r0)
vc =   6.6287e+03
>> vm=sqrt(2*G*M*R/(r0*(r0+R)))
vm =   6.0213e+03

Trayectoria exterior

La ecuación de la trayectoria en coordenadas polares es

${\displaystyle \begin{array}{l}r=\frac{d}{1+\epsilon \cos \theta }\\ \epsilon =\sqrt{1+\frac{2L^{2}E}{G^2{M}^2{m}^3}}=\sqrt{1+\frac{r_0{v}_0^2\left(r_0{v}_0^2-2GM\right)}{G^2{M}^2}}\\ d=\frac{L^2}{GM{m}^2}=\frac{r_0^2{v}_0^2}{GM}\end{array}}$

Punto de impacto

Determinamos la intersección P de la trayectoria elíptica con la superficie de la Tierra

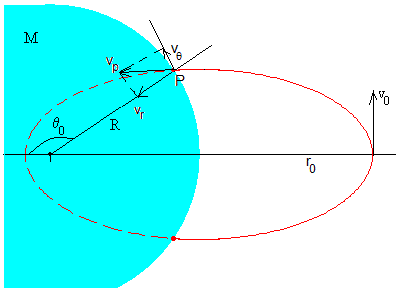
En coordenadas polares, el proyectil sale de la posición r₀, θ=π, y llega a la posición R, θ₀, donde

${\displaystyle R=\frac{d}{1+\epsilon \cos {\theta }_0}\cos {\theta }_0=\frac{d-R}{R\epsilon }}$

Las coordenadas del punto P son: x_p=Rcosθ₀, y_p=Rsinθ₀.

Calculamos el módulo de la velocidad del proyectil en el punto P a partir del principio de conservación de la energía.

${\displaystyle \begin{array}{l}\frac{1}{2}m{v}_0^2-\frac{GmM}{r_0}=\frac{1}{2}m{v}_p^2-\frac{GmM}{R}\\ v_p^2=v_0^2+2GM\left(\frac{1}{R}-\frac{1}{r_0}\right)\end{array}}$

A partir de la constancia del momento angular, calculamos la componente v_θ de la velocidad

${\displaystyle \begin{array}{l}L=mr\left(r\frac{d\theta }{dt}\right)\\ r_0{v}_0=R{v}_{\theta }\end{array}}$

Ahora la componente radial v_r

${\displaystyle v_p^2=v_r^2+v_{\theta }^2}$

Las componentes rectangulares v_x y v_y del vector velocidad en el punto P son (véase la figura anterior):

${\displaystyle \{\begin{array}{l}{v}_x=-v_r\cos \left(\pi -{\theta }_0\right)-v_{\theta }\sin \left(\pi -{\theta }_0\right)\\ v_y=-v_r\sin \left(\pi -{\theta }_0\right)+v_{\theta }\cos \left(\pi -{\theta }_0\right)\end{array}}$

El alcance del proyectil es el arco sobre la superficie de la Tierra correspondiente al ángulo π-θ₀, s=R(π-θ₀)

Tiempo de vuelo

Calculamos el instante de impacto empleando la ecuación de Kepler

• Se calcula el tiempo t₀ para posición angular π
• Se calcula el tiempo t₁ para posición θ₀

Dada la posición angular θ, determinamos el ángulo E mediante las relaciones

${\displaystyle \sin E=\frac{\sqrt{1-{\epsilon }^2}\sin \theta }{1+\epsilon \cos \theta }\cos E=\frac{\epsilon +\cos \theta }{1+\epsilon \cos \theta }}$

Dependiendo del signo del seno y del coseno, se determina el cuadrante y se calcula el ángulo E. Sustituyendo en la ecuación de Kepler, obtenemos M_e

${\displaystyle M_e=E-\epsilon \sin E}$

Conocido M_e, obtenemos el tiempo τ hasta que impacta en la superficie de la Tierra

${\displaystyle \tau =\frac{M_e}{2\pi }P{P}^2=\frac{4{\pi }^2}{GM}{a}^3}$

Desde una altura h=2000 km, lanzamos un proyectil con velocidad v₀=2000 m/s en la dirección tangencial. Calculamos el tiempo de vuelo y el alcance

R=6371*1000; %radio de la Tierra
M=5.972e24; %masa de la Tierra
G=6.674e-11; %constante G

h=2000*1000; %altura de disparo
r0=R+h; %desde el centro de la Tierra
hold on
ang=(1:360)*pi/180;
fill(cos(ang),sin(ang),'c') %la Tierra

%trayectoria en el exterior
v0=2*1000; %velocidad de disparo
d=r0^2*v0^2/(G*M); 
e=sqrt(1+r0*v0^2*(r0*v0^2-2*G*M)/(G*M)^2);
E=v0^2/2-G*M/r0;
r=@(x) d./(1+e*cos(x));
plot(r(ang).*cos(ang)/R, r(ang).*sin(ang)/R, 'r','lineStyle','--')
plot (0,0,'o','markersize',4,'markeredgecolor','b','markerfacecolor','b')

%punto de impacto
th_0=acos((d-R)/(R*e));
plot (cos(th_0),sin(th_0),'o','markersize',4,'markeredgecolor',
'r','markerfacecolor','r')
ang=(th_0*180/pi:180)*pi/180;
plot(r(ang).*cos(ang)/R, r(ang).*sin(ang)/R,'r')
line([0,-r0/R],[0,0],'color','k','lineStyle','--')
line([0,r(th_0)*cos(th_0)/R],[0,r(th_0)*sin(th_0)/R],'color','k','lineStyle','--')

r1=(r0*v0)^2/(2*G*M-r0*v0^2);
c=(r0-r1)/2; %semidistancia focal
a=(r0+r1)/2; %semieje mayor
th=pi;
s_E=sqrt(1-e^2)*sin(th)/(1+e*cos(th));
c_E=(e+cos(th))/(1+e*cos(th));
E=atan2(s_E,c_E);
if E<0
    E=2*pi+E;
end
t1=(E-e*s_E)*a^(3/2)/sqrt(G*M);
th=th_0;
s_E=sqrt(1-e^2)*sin(th)/(1+e*cos(th));
c_E=(e+cos(th))/(1+e*cos(th));
E=atan2(s_E,c_E);
if E<0
    E=2*pi+E;
end
t2=(E-e*s_E)*a^(3/2)/sqrt(G*M);
fprintf('El tiempo de vuelo es %2.1f min, alcance es %4.1f km\n'
,(t1-t2)/60,(pi-th_0)*R/1000)
hold off
axis equal

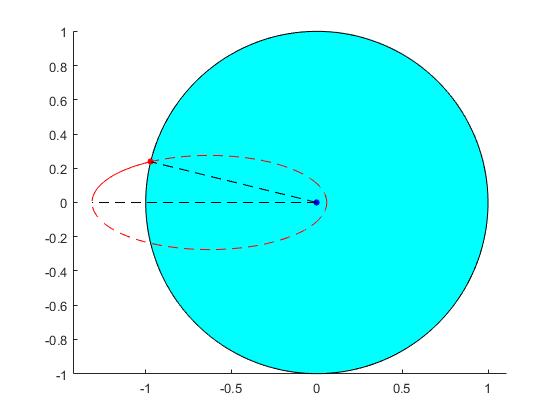
El tiempo de vuelo es 14.0 min, alcance es 1532.5 km

Actividades

Se introduce

• La altura en kilómetros sobre la superficie de la Tierra desde la que lanzamos un proyectil, perpendicularmente a la dirección radial, en el control titulado Altura (km)
• La velocidad con que se lanza el proyectil, en el control titulado Velocidad (m/s).

Se pulsa el botón titulado Nuevo

Se representa la trayectoria seguida por el proyectil. Si impacta en la superficie de la Tierra, se calcula el alcance o longitud del arco del meridiano terrestre comprendido entre la dirección radial de disparo y la dirección radial de impacto.

Ejemplos:

Comprobamos que un proyectil disparado horizontalmente en lo alto de una montaña situada en el polo Norte, no puede caer más allá del polo Sur. Si se le proporciona una velocidad adicional el proyectil rodeará la Tierra.

Para comprobarlo, introducir los siguientes datos en los respectivos controles

• Altura 30000 km
• Velocidad de disparo 1808 y 1809 m/s

Calculamos la velocidad de disparo para que el proyectil describa una trayectoria circular de altura h=20000 km

• Masa de la Tierra M=5.98·10²⁴ kg
• Radio de la Tierra, R=6.37·10⁶ m
• Constante G=6.67·10^-11 Nm²/kg²

${\displaystyle \frac{m{v}^2}{r}=G\frac{Mm}{r^2}v=\sqrt{\frac{GM}{r}}=\sqrt{\frac{6.67·{10}^{-11}·5.98·{10}^{24}}{(6.37·{10}^6+20·{10}^6)}}=3889.2\text{m/s}}$

Cuando la altura es pequeña, por ejemplo 20 km o menos, la superficie de la Tierra aparece plana, la trayectoria elíptica se aproxima a la parábola que describe un cuerpo bajo la aceleración constante de la gravedad. Calculamos el alcance aplicando las ecuaciones del tiro parabólico.

Un proyectil se dispara desde una altura de h=20 km, con una velocidad de v=30 m/s, calcular el alcance. Tómese g=9.8 m/s²

${\displaystyle \begin{array}{l}h=\frac{1}{2}g{t}^2\text{}x=vt\\ 20000=\frac{1}{2}9.8t^{2}x=30t=1917\text{m}\end{array}}$

Trayectoria interior

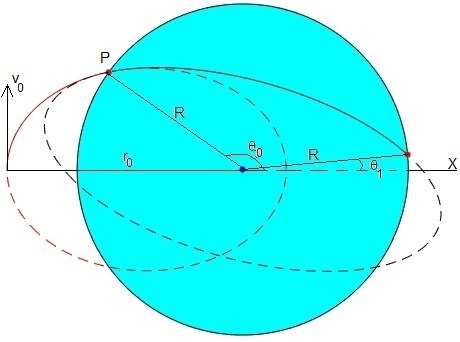
Una vez que el móvil se encuentra en P, sigue una trayectoria elíptica bajo la acción de una fuerza atractiva proporcional a la distancia al centro de la Tierra

La posición de la partícula respecto del tiempo es

${\displaystyle \begin{array}{l}x=A_x\sin (\omega t)+B_x\cos (\omega t)\\ y=A_y\sin (\omega t)+B_y\cos (\omega t)\end{array}\}\omega =\sqrt{G\frac{M}{R^3}}}$

Las componentes de la velocidad de la partícula son

${\displaystyle \{\begin{array}{l}\frac{dx}{dt}=\omega (A_x\cos (\omega t)-B_x\sin (\omega t))\\ \frac{dy}{dt}=\omega (A_y\cos (\omega t)-B_y\sin (\omega t))\end{array}}$

Las constantes A_x, A_y, B_x y B_y se determinan a partir de las condiciones iniciales, en el instante t=0, el proyectil entra en la Tierra en la posición x_p=Rcosθ₀, y_p=Rsinθ₀, con velocidades

${\displaystyle \{\begin{array}{l}{v}_x=-v_r\cos \left(\pi -{\theta }_0\right)-v_{\theta }\sin \left(\pi -{\theta }_0\right)\\ v_y=-v_r\sin \left(\pi -{\theta }_0\right)+v_{\theta }\cos \left(\pi -{\theta }_0\right)\end{array}}$

Los coeficientes valen

${\displaystyle \{\begin{array}{l}{A}_x=\frac{v_x}{\omega }{A}_y=\frac{v_y}{\omega }\\ B_x=x_p{B}_y=y_p\end{array}}$

La intersección entre la trayectoria elíptica y la circunferencia de radio R nos proporciona el tiempo t₁ que tarda el proyectil en salir del interior de la Tierra. La ecuación de la circunferencia es, x²+y²=R²

${\displaystyle \begin{array}{l}\left(A_x^2+A_y^2\right){\sin }^2\left(\omega t\right)+\left(B_x^2+B_y^2\right){\cos }^2\left(\omega t\right)+2\left(A_x{B}_x+A_y{B}_y\right)\sin \left(\omega t\right)\cos \left(\omega t\right)=R^2\\ {\left(\frac{v_p}{\omega }\right)}^2{\sin }^2\left(\omega t\right)+R^2{\cos }^2\left(\omega t\right)+2\left(A_x{B}_x+A_y{B}_y\right)\sin \left(\omega t\right)\cos \left(\omega t\right)=R^2\\ \left\{{\left(\frac{v_p}{\omega }\right)}^2-R^2\right\}\sin \left(\omega t\right)+2\left(A_x{B}_x+A_y{B}_y\right)\cos \left(\omega t\right)=0\\ \tan \left(\omega t\right)=\frac{2\left(A_x{B}_x+A_y{B}_y\right)}{R^2-{\left(\frac{v_p}{\omega }\right)}^2}\end{array}}$

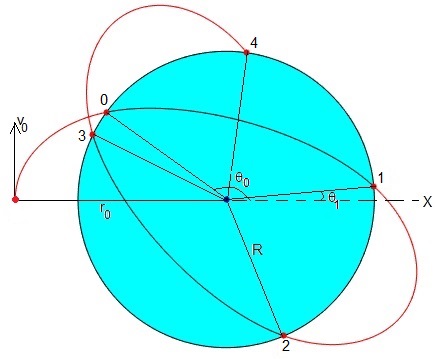
En el siguiente script representamos en color rojo la trayectoria seguida por un proyectil que es disparado con velocidad de 3.70 km/s desde una altura de 2700 km, la línea a puntos completa la trayectoria elíptica que seguiría el proyectil si la Tierra fuese una masa puntual. El punto de color rojo señala el impacto del proyectil sobre la superficie de la Tierra cuya posición angular es θ₀.

Una vez que llega a la superficie, el proyectil describe una porción de trayectoria elíptica girada, señalada en color negro en la figura. La trayectoria del proyectil en el interior de la Tierra se representa mediante una línea continua. La variable t1 guarda el tiempo que tarda en alcanzar la superficie de la Tierra desde el interior

R=6371*1000; %radio de la Tierra
M=5.972e24; %masa de la Tierra
G=6.674e-11; %constante G

h=2700*1000; %altura de disparo
r0=R+h; %desde el centro de la Tierra
hold on
ang=(1:360)*pi/180;
fill(cos(ang),sin(ang),'c') %la Tierra

%trayectoria en el exterior
v0=3.70*1000; %velocidad de disparo
d=r0^2*v0^2/(G*M); 
e=sqrt(1+r0*v0^2*(r0*v0^2-2*G*M)/(G*M)^2);
E=v0^2/2-G*M/r0;
r=@(x) d./(1+e*cos(x));
plot(r(ang).*cos(ang)/R, r(ang).*sin(ang)/R, 'r','lineStyle','--')
plot (0,0,'o','markersize',4,'markeredgecolor','b','markerfacecolor','b')

%punto de impacto
th_0=acos((d-R)/(R*e));
plot (cos(th_0),sin(th_0),'o','markersize',4,'markeredgecolor','r',
'markerfacecolor','r')
ang=(th_0*180/pi:180)*pi/180;
plot(r(ang).*cos(ang)/R, r(ang).*sin(ang)/R,'r')
%velocidades
vp=sqrt(v0^2+2*G*M*(1/R-1/r0));
v_th=r0*v0/R;
vr=sqrt(vp^2-v_th^2);

%trayectoria en el interior de la Tierra
vx=vr*cos(pi-th_0)+v_th*sin(pi-th_0);
vy=-vr*sin(pi-th_0)+v_th*cos(pi-th_0);
w=sqrt(G*M/R^3);
Ax=vx/w; Ay=vy/w;
Bx=R*cos(th_0); By=R*sin(th_0);
%tiempo hasta que llega a la superficie
t1=(atan(2*(Ax*Bx+Ay*By)/(R^2-(vp/w)^2))+pi)/w; 
fplot(@(t) (Ax*sin(w*t)+Bx*cos(w*t))/R, @(t) (Ay*sin(w*t)+By*cos(w*t))/R,
[0,2*pi/w], 'lineStyle','--','color','k')
fplot(@(t) (Ax*sin(w*t)+Bx*cos(w*t))/R, @(t) (Ay*sin(w*t)+By*cos(w*t))/R,
[0,t1],'color','k')
hold off
axis equal

Ecuación de la trayectoria interior

Vamos a dibujar la trayectoria del proyectil en el interior de la Tierra usando ecuación de la trayectoria en coordenadas polares

${\displaystyle r^2=\frac{d\text{'}}{1+\epsilon \text{'}\cos \left(2(\theta -{\phi }_0)\right)}\epsilon \text{'}=\sqrt{1-\frac{GM{L}^2}{R^{3}E{\text{'}}^2}}d\text{'}=\frac{L^2}{mE\text{'}}}$

Donde E' es la energía E del proyectil disparado más una cantidad adicional

${\displaystyle E^{\text{'}}=E+\frac{3}{2}\frac{GMm}{R}}$

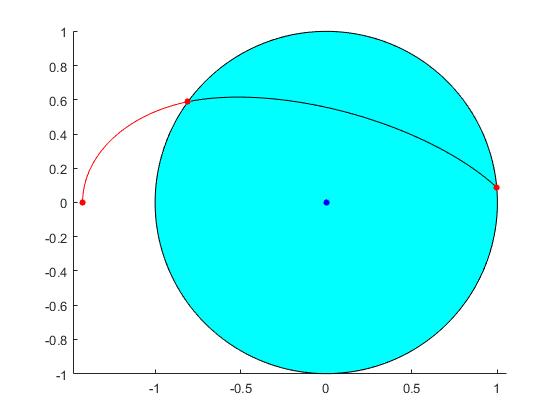
Se calcula el ángulo φ₀ a partir de la posición de partida (R, θ₀). El punto P de impacto que se ha producido cuando r=R, en la posición angular θ₀ ya calculado en la sección anterior y que es el punto de entrada del proyectil en el interior de la Tierra

${\displaystyle R^2=\frac{d\text{'}}{1+\epsilon \text{'}\cos \left(2({\theta }_0-{\phi }_0)\right)}{\phi }_0={\theta }_0-\frac{1}{2}\arccos \frac{d\text{'}-R^2}{\epsilon \text{'}{R}^2}}$

La intersección de esta trayectoria con la superficie esférica, se produce para el ángulo θ₁, que es la posición angular de salida del proyectil de la Tierra. Dado que para θ=θ₀, r=R y para θ=θ₁, r=R, se tendrá que cumplir que

${\displaystyle \begin{array}{l}\cos \left(2({\theta }_1-{\phi }_0)\right)=\cos \left(2({\theta }_0-{\phi }_0)\right)\hfill \\ 2({\theta }_1-{\phi }_0)=-2({\theta }_0-{\phi }_0)\hfill \\ {\theta }_1=2{\phi }_0-{\theta }_0\hfill \end{array}}$

Creamos un script alternativo para representar las trayectorias de la figura al principio de este apartado

R=6371*1000; %radio de la Tierra
M=5.972e24; %masa de la Tierra
G=6.674e-11; %constante G

h=2700*1000; %altura de disparo
r0=R+h; %desde el centro de la Tierra
hold on
plot (-r0/R,0,'o','markersize',4,'markeredgecolor','r','markerfacecolor','r')
ang=(1:360)*pi/180;
fill(cos(ang),sin(ang),'c') %la Tierra
plot (0,0,'o','markersize',4,'markeredgecolor','b','markerfacecolor','b')

%trayectoria en el exterior
v0=3.70*1000; %velocidad de disparo
d=r0^2*v0^2/(G*M); 
e=sqrt(1+r0*v0^2*(r0*v0^2-2*G*M)/(G*M)^2);
E=v0^2/2-G*M/r0;
r=@(x) d./(1+e*cos(x));
%intersección
th_0=acos((d-R)/(R*e));
plot (cos(th_0),sin(th_0),'o','markersize',4,'markeredgecolor',
'r','markerfacecolor','r')
ang=(th_0*180/pi:180)*pi/180;
plot(r(ang).*cos(ang)/R, r(ang).*sin(ang)/R,'r')

%trayectoria en el interior 
Ep=E+3*G*M/(2*R);
ep=sqrt(1-G*M*(r0*v0)^2/(R^3*Ep^2));
dp=(r0*v0)^2/Ep;
phi_0=th_0-acos((dp-R^2)/(ep*R^2))/2; 
th_1=2*phi_0-th_0;
ang=(th_1*180/pi:th_0*180/pi)*pi/180;
r2=@(x) dp./(1+ep*cos(2*(x-phi_0)));
plot(sqrt(r2(ang)).*cos(ang)/R, sqrt(r2(ang)).*sin(ang)/R,'k')
ang=(th_0*180/pi:360+th_1*180/pi)*pi/180;
plot (cos(th_1),sin(th_1),'o','markersize',4,'markeredgecolor',
'r','markerfacecolor','r')
hold off
axis equal

Trayectorias exteriores e interiores

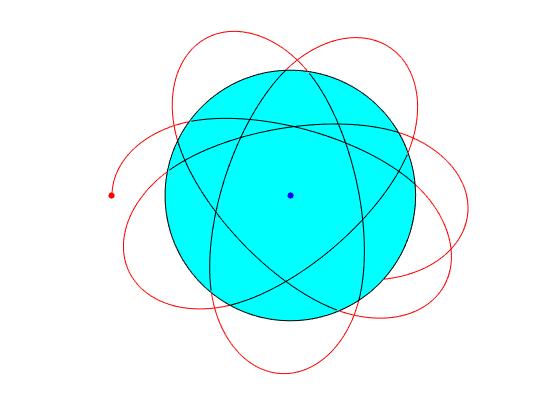
Una vez que hemos aprendido a trazar y conectar una trayectoria exterior a la Tierra y una trayectoria interior, vamos a continuar el proceso de forma indefinida tal como se muestra en la figura.

Vamos a resumir los pasos

• Trayectoria inicial exterior

${\displaystyle r=\frac{d}{1+\epsilon \cos \left(\theta -{\phi }_e\right)}\epsilon =\sqrt{1+\frac{2L^{2}E}{G^2{M}^2{m}^3}}d=\frac{L^2}{GM{m}^2}}$

Donde el ángulo φ_e se determina a partir de la posición de partida que en nuestro caso es: θ=π, r=r₀, por lo que φ_e=0

Cuando el proyectil impacta en la superficie de la Tierra, el ángulo θ₀ para el que r=R es

${\displaystyle R=\frac{d}{1+\epsilon \cos \left({\theta }_0-{\phi }_e\right)}{\theta }_0={\phi }_e+\arccos \left(\frac{d-R}{R\epsilon }\right)}$

La posición (R, θ₀) es la posición de partida para la trayectoria interior

• Trayectoria interior

${\displaystyle r^2=\frac{d\text{'}}{1+\epsilon \text{'}\cos \left(2(\theta -{\phi }_i)\right)}\epsilon \text{'}=\sqrt{1-\frac{GM{L}^2}{R^{3}E{\text{'}}^2}}d\text{'}=\frac{L^2}{mE\text{'}}}$

Donde E' es la energía E del proyectil disparado más una cantidad adicional necesaria para ajustar el nivel cero de energía potencial en el infinito

${\displaystyle E^{\text{'}}=E+\frac{3}{2}\frac{GMm}{R}}$

El ángulo φ_i se determina a partir de la posición inicial de esta trayectoria (R, θ₀)

${\displaystyle R^2=\frac{d\text{'}}{1+\epsilon \text{'}\cos \left(2({\theta }_0-{\phi }_i)\right)}{\phi }_i={\theta }_0-\frac{1}{2}\arccos \left(\frac{d\text{'}-R^2}{R^2\epsilon \text{'}}\right)}$

La otra intersección de la trayectoria interior con la superficie de la Tierra r=R, marca el final de la trayectoria interior y el comienzo de la exterior

${\displaystyle \begin{array}{l}{R}^2=\frac{d\text{'}}{1+\epsilon \text{'}\cos \left(2({\theta }_0-{\phi }_i)\right)}{R}^2=\frac{d\text{'}}{1+\epsilon \text{'}\cos \left(2({\theta }_1-{\phi }_i)\right)}\\ \cos \left(2({\theta }_1-{\phi }_i)\right)=\cos \left(2({\theta }_0-{\phi }_i)\right)\\ {\theta }_1-{\phi }_i=-\left({\theta }_0-{\phi }_i\right)\\ {\theta }_1=2{\phi }_i-{\theta }_0\end{array}}$

• Trayectoria exterior

${\displaystyle r=\frac{d}{1+\epsilon \cos \left(\theta -{\phi }_e\right)}}$

El ángulo φ_e se determina a partir de la posición inicial (R, θ₁). Teniendo en cuenta que arccos(k)=±θ (en este caso, tomamos el signo negativo)

${\displaystyle R=\frac{d}{1+\epsilon \cos \left({\theta }_1-{\phi }_e\right)}{\phi }_e={\theta }_1+\arccos \left(\frac{d-R}{R\epsilon }\right)}$

La otra intersección de la trayectoria interior con la superficie de la Tierra r=R, marca el final de la trayectoria exterior y el comienzo de la interior

${\displaystyle \begin{array}{l}R=\frac{d}{1+\epsilon \cos \left({\theta }_1-{\phi }_e\right)}R=\frac{d}{1+\epsilon \cos \left({\theta }_2-{\phi }_e\right)}\\ \cos \left({\theta }_2-{\phi }_e\right)=\cos \left({\theta }_1-{\phi }_e\right)\\ {\theta }_2-{\phi }_e=-\left({\theta }_1-{\phi }_e\right)-2\pi \\ {\theta }_2=2{\phi }_e-{\theta }_1-2\pi \end{array}}$

• Se vuelve a la trayectoria interior con θ₀=θ₂ y así, sucesivamente

R=6371*1000; %radio de la Tierra
M=5.972e24; %masa de la Tierra
G=6.674e-11; %constante G

h=2700*1000; %altura de disparo
r0=R+h; %desde el centro de la Tierra
hold on
ang=(1:360)*pi/180;
fill(cos(ang),sin(ang),'c') %la Tierra
plot (-r0/R,0,'o','markersize',4,'markeredgecolor',
'r','markerfacecolor','r')
plot (0,0,'o','markersize',4,'markeredgecolor','b',
'markerfacecolor','b')

%trayectoria en el exterior
v0=3.70*1000; %velocidad de disparo
d=r0^2*v0^2/(G*M); 
e=sqrt(1+r0*v0^2*(r0*v0^2-2*G*M)/(G*M)^2);
E=v0^2/2-G*M/r0;

%trayectoria en el interior 
Ep=E+3*G*M/(2*R);
ep=sqrt(1-G*M*(r0*v0)^2/(R^3*Ep^2));
dp=(r0*v0)^2/Ep;

%trayectoria exterior (inicial)
th_0=acos((d-R)/(R*e));
r=@(x) d./(1+e*cos(x));
ang=(th_0*180/pi:180)*pi/180;
plot(r(ang).*cos(ang)/R, r(ang).*sin(ang)/R,'r')

for i=1:6
%trayectoria interior
    phi_i=th_0-acos((dp-R^2)/(ep*R^2))/2;
    th_1=2*phi_i-th_0; 
    ang=(th_1*180/pi:th_0*180/pi)*pi/180;
    r2=@(x) dp./(1+ep*cos(2*(x-phi_i)));
    plot(sqrt(r2(ang)).*cos(ang)/R, sqrt(r2(ang)).*sin(ang)/R,'k')

  %trayectoria exterior
    phi_e=th_1+acos((d-R)/(R*e));
    th_2=2*phi_e-th_1-2*pi; 
    r=@(x) d./(1+e*cos(x-phi_e));
    ang=(th_2*180/pi:th_1*180/pi)*pi/180;
    plot(r(ang).*cos(ang)/R, r(ang).*sin(ang)/R,'r')
    th_0=th_2;
end

hold off
axis equal
axis off

Mediante el siguiente script podremos cambiar fácilmente los parámetros (d', ε', d, ε) de la trayectoria interior y exterior y observamos el resultado. Para reproducir la figura anterior ponemos los parámetros d y d' en unidades del radio de la Tierra R. Definimos los ángulos

${\displaystyle \delta =\arccos \left(\frac{d/R-1}{\epsilon }\right){\delta }_p=\frac{1}{2}\arccos \left(\frac{d\text{'}/R^2-1}{\epsilon \text{'}}\right)}$

Para cada iteracción i, calculamos los ángulos, φ_i y θ₁ de la trayectoria interior

${\displaystyle \{\begin{array}{l}{\phi }_i={\theta }_0-(2i-1){\delta }_p+2(i-1)\delta -2(i-1)\pi \\ {\theta }_1={\theta }_0-2i·{\delta }_p+2(i-1)\delta -2(i-1)\pi \end{array}}$

los ángulos, φ_e y θ₂ de la trayectoria exterior

${\displaystyle \{\begin{array}{l}{\phi }_e={\theta }_0-2i·{\delta }_p+(2i-1)\delta -2(i-1)\pi \\ {\theta }_2={\theta }_0-2i·{\delta }_p+2i·\delta -2i\pi \end{array}}$

hold on
ang=(1:360)*pi/180;
fill(cos(ang),sin(ang),'c') %la Tierra
plot (0,0,'o','markersize',4,'markeredgecolor','b','markerfacecolor','b')

%trayectoria en el interior 
ep=0.6788; %excentricidad
dp=0.4891; %parámetro d
%trayectoria en el exterior
e=0.6884; %excentricidad
d=0.4436;  %parámetro d

n=6;
delta_p=acos((dp-1)/ep)/2;
delta=acos((d-1)/e);

%trayectoria exterior (inicial)
th_0=delta;
r=@(x) d./(1+e*cos(x));
ang=(th_0*180/pi:180)*pi/180;
plot(r(ang).*cos(ang), r(ang).*sin(ang),'r')

th_2=th_0;
for i=1:n
%trayectoria interior
    phi_i=th_0-(2*i-1)*delta_p+2*(i-1)*delta-2*(i-1)*pi; %th_0-delta_p;
    th_1=th_0-2*i*delta_p+2*(i-1)*delta-2*(i-1)*pi; %2*phi_i-th_0; 
    ang=(th_1*180/pi:th_2*180/pi)*pi/180;
    r2=@(x) dp./(1+ep*cos(2*(x-phi_i)));
    plot(sqrt(r2(ang)).*cos(ang), sqrt(r2(ang)).*sin(ang),'k')

  %trayectoria exterior
    phi_e=th_0-2*i*delta_p+(2*i-1)*delta-2*(i-1)*pi;
    th_2=th_0-2*i*delta_p+2*i*delta-2*i*pi; %2*phi_e-th_1-2*pi;
    r=@(x) d./(1+e*cos(x-phi_e));
    ang=(th_2*180/pi:th_1*180/pi)*pi/180;
    plot(r(ang).*cos(ang), r(ang).*sin(ang),'r')
end

hold off
axis equal
axis off

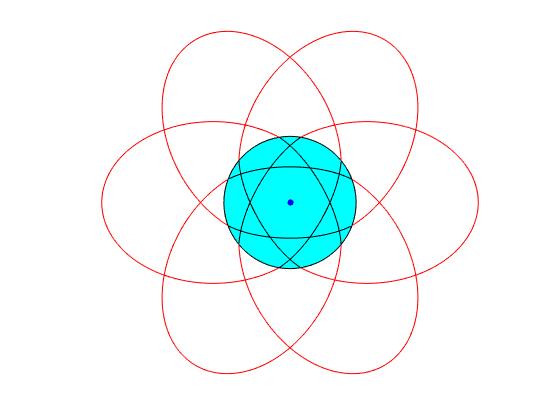
Trayectorias cerradas

El eje de la primera trayectoria exterior es horizontal, tiene un ángulo φ_e=0. Para que la trayectoria se cierre, el ángulo del eje φ_e de la trayectoria exterior tiene que ser un múltiplo de 2π, φ_e=-2nπ. Teniendo en cuenta que el ángulo θ₀=δ

${\displaystyle \begin{array}{l}{\theta }_0-2i·{\delta }_p+(2i-1)\delta -(2i-1)\pi =-2n\pi \\ -2i·{\delta }_p+2i\delta -2(i-1)\pi =-2n\pi \\ \delta ={\delta }_p+\frac{i-1-n}{i}\pi \end{array}}$

Si elegimos modificar el parámetro d de la trayectoria exterior

${\displaystyle \begin{array}{l}\frac{d/R-1}{\epsilon }=\cos \left({\delta }_p+\frac{i-1-n}{i}\pi \right)\\ \frac{d}{R}=1+\epsilon \cos \left({\delta }_p+\frac{i-1-n}{i}\pi \right)\end{array}}$

Por ejemplo, queremos que la trayectoria se cierre en la última iteracción, cuando i=n

${\displaystyle \frac{d}{R}=1+\epsilon \cos \left({\delta }_p-\frac{\pi }{n}\right)}$

hold on
ang=(1:360)*pi/180;
fill(cos(ang),sin(ang),'c') %la Tierra
plot (0,0,'o','markersize',4,'markeredgecolor','b','markerfacecolor','b')

%trayectoria en el interior 
ep=0.6788; %excentricidad
dp=0.4891; %parámetro d
%trayectoria en el exterior
e=0.6884; %excentricidad
d=0.4436;  %parámetro d

n=6;
delta_p=acos((dp-1)/ep)/2;
d=1+e*cos(delta_p+pi/n); %para que se cierre la trayectoria
delta=acos((d-1)/e);

%trayectoria exterior (inicial)
th_0=delta;
r=@(x) d./(1+e*cos(x));
ang=(th_0*180/pi:180)*pi/180;
plot(r(ang).*cos(ang), r(ang).*sin(ang),'r')

th_2=th_0;
for i=1:n
%trayectoria interior
    phi_i=th_0-(2*i-1)*delta_p+2*(i-1)*delta-2*(i-1)*pi; %th_0-delta_p;
    th_1=th_0-2*i*delta_p+2*(i-1)*delta-2*(i-1)*pi; %2*phi_i-th_0; 
    ang=(th_1*180/pi:th_2*180/pi)*pi/180;
    r2=@(x) dp./(1+ep*cos(2*(x-phi_i)));
    plot(sqrt(r2(ang)).*cos(ang), sqrt(r2(ang)).*sin(ang),'k')

  %trayectoria exterior
    phi_e=th_0-2*i*delta_p+(2*i-1)*delta-2*(i-1)*pi;
    th_2=th_0-2*i*delta_p+2*i*delta-2*i*pi; %2*phi_e-th_1-2*pi;
    r=@(x) d./(1+e*cos(x-phi_e));
    ang=(th_2*180/pi:th_1*180/pi)*pi/180;
    plot(r(ang).*cos(ang), r(ang).*sin(ang),'r')
end

hold off
axis equal
axis off

Referencias

W. Dean Pesnell. The flight of Newton's cannonball. Am. J. Phys. 86 (5) May 2018, pp. 338-343

H. X. Jiang, J. Y. Lin. Precession of Kepler's orbit. Am. J. Phys. 53(7) July 1985, pp. 694-695