La Tierra tiene masa M=5.98·10²⁴ kg y radio R=6.37·10⁶ m, supondremos no gira sobre su eje.

Movimiento del satélite

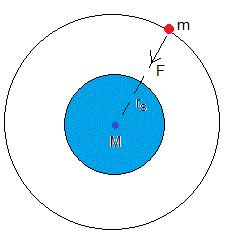
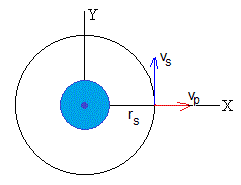
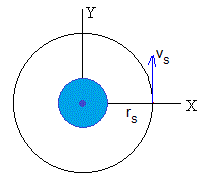
Sea un satélite de masa m que describe una órbita circular de radio r_s

La ecuación de la dinámica del movimiento circular uniforme (fuerza de atracción igual a masa por aceleración normal), se escribe

${\displaystyle \begin{array}{l}G\frac{Mm}{r_s^2}=m\frac{v_s^2}{r_s}\\ v_s=\sqrt{\frac{GM}{r_s}}\end{array}}$

Donde v_s es la velocidad constante del satélite

La órbita de un satélite cuyo periodo es un día se denomina geoestacionaria, su velocidad angular es la misma que la de rotación de la Tierra

${\displaystyle \begin{array}{l}P=\frac{2\pi r_s}{v_s}=\frac{2\pi r_s\sqrt{r_s}}{\sqrt{GM}}\\ P^2=4{\pi }^2\frac{r_s^3}{GM}\end{array}}$

Si P=24·60·60, entonces r_s=42 250 km=6.63·R

Movimiento del proyectil en la dirección radial

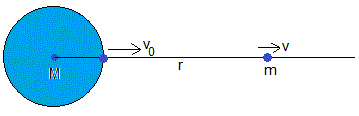
Sea un proyectil de masa m que se dispara desde la superficie de la Tierra con velocidad v₀ en dirección radial. Pueden ocurrir los siguientes casos:

La velocidad inicial del proyectil es inferior a la de escape

Supongamos que la velocidad de disparo del proyectil es menor que la velocidad de escape, v₀<v_e

El proyectil se detiene cuando dista del centro de la Tierra r_m y regresa a la superficie de la Tierra con la misma velocidad de disparo.

${\displaystyle \begin{array}{l}\frac{1}{2}m{v}_0^2-G\frac{Mm}{R}=-G\frac{Mm}{r_m}\\ r_m=\frac{2GMR}{2GM-R{v}_0^2}\end{array}}$

Si r_m<r_s el proyectil no alcanza al satélite. En caso contrario, si r_m>r_s calculamos la velocidad del proyectil v_p cuando alcanza la órbita del satélite.

${\displaystyle \frac{1}{2}m{v}_0^2-G\frac{Mm}{R}=\frac{1}{2}m{v}_p^2-G\frac{Mm}{r_s}}$

Se denomina velocidad de escape v_e, la mínima necesaria para salir del campo gravitatorio de la Tierra, es decir, para alcanzar el infinito con velocidad nula

${\displaystyle \frac{1}{2}m{v}_e^2-G\frac{Mm}{R}=0v_e=\sqrt{\frac{2GM}{R}}}$

La velocidad v del proyectil cuando está a una distancia r del centro de la Tierra es

${\displaystyle \frac{1}{2}m{v}_0^2-G\frac{Mm}{R}=\frac{1}{2}m{v}^2-G\frac{Mm}{r}}$

Despejamos v=dr/dt en función r

${\displaystyle \begin{array}{l}{\left(\frac{dr}{dt}\right)}^2=v_0^2-2GM\left(\frac{1}{R}-\frac{1}{r}\right)\\ t={\displaystyle \underset{R}{\overset{r}{\int }}\sqrt{\frac{rR}{a-br}}dr}\{\begin{array}{l}a=2GMR\\ b=2GM-R{v}_0^2\end{array}\end{array}}$

Se hace el cambio de variable

${\displaystyle r=\frac{a}{b}{\sin }^2\theta }$

Quedando la integral,

${\displaystyle \begin{array}{l}t=\frac{2\sqrt{R}a}{b\sqrt{b}}{\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}{\sin }^2\theta \cdot d\theta }\\ t=\frac{\sqrt{R}a}{b\sqrt{b}}\left(\theta -\frac{1}{2}\sin \left(2\theta \right)-{\theta }_0+\frac{1}{2}\sin \left(2{\theta }_0\right)\right)\end{array}}$

• Disparamos un proyectil de masa m desde la superficie de la Tierra con velocidad v₀=0.9·v_e, calcular la máxima distancia r_m al centro de la Tierra y el tiempo t que tarda en alcanzarla.

GM=6.67e-11*5.98e24;
R=6.37e6; %radio de la Tierra
ve=sqrt(2*GM/R); %velocidad de escape
v0=0.9*ve; %velocidad de disparo del proyectil
a=2*GM*R;
b=2*GM-R*v0^2;
rm=a/b; %máximo alejamiento del centro de la Tierra
phi_0=asin(sqrt(b*R/a));
phi=asin(sqrt(b*rm/a));
t=sqrt(R)*a*(phi-sin(2*phi)/2-phi_0+sin(2*phi_0)/2)/b^(3/2);
fprintf('La máxima distancia es %3.2f·R, y el tiempo %3.2f min\n',rm/R,t/60);

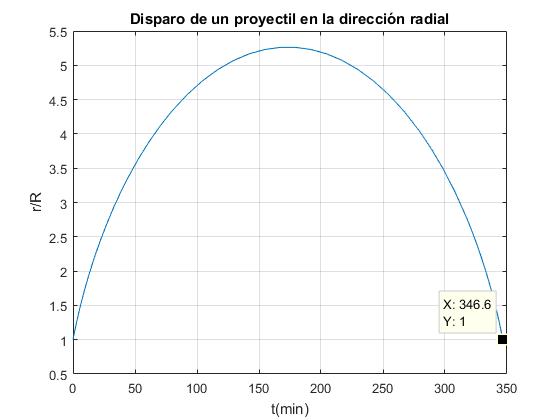
La máxima distancia es 5.26·R, y el tiempo 173.21 min

La máxima distancia que el proyectil se aleja del centro de la Tierra es 5.26·R=33526 km y emplea un tiempo de t=173.21 minutos

• Disparamos un proyectil de masa m desde la superficie de la Tierra con velocidad v₀=0.9·v_e, calcular la velocidad del proyectil cuando se encuentra a una distancia r_s=5·R del centro de la Tierra y el tiempo t que tarda en alcanzar esta posición.

GM=6.67e-11*5.98e24;
R=6.37e6; %radio de la Tierra
ve=sqrt(2*GM/R); %velocidad de escape
v0=0.9*ve; %velocidad de disparo del proyectil
rS=5*R;    
v=sqrt(v0^2-2*GM*(1/R-1/rS));
a=2*GM*R;
b=2*GM-R*v0^2;
phi_0=asin(sqrt(b*R/a));
phi=asin(sqrt(b*rS/a));
t=sqrt(R)*a*(phi-sin(2*phi)/2-phi_0+sin(2*phi_0)/2)/b^(3/2);
fprintf('La velocidad es %3.2f m/s, y el tiempo %3.2f min\n',v,t/60);

La velocidad es 1119.07 m/s, y el tiempo 122.41 min

La velocidad del proyectil cuando se ha alejado del centro de la Tierra 5·R es v_p=1119 m/s y emplea un tiempo de t=122.41 minutos en alcanzar esta posición

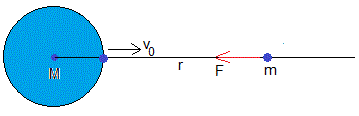
La velocidad inicial del proyectil es mayor que la de escape

Supongamos que la velocidad de disparo del proyectil es mayor que la velocidad de escape, v₀>v_e

${\displaystyle \begin{array}{l}{v}_0^2>v_e^2\\ v_0^{2}R>2GM\end{array}}$

El parámetro b ahora es negativo, y hay que buscar otro procedimiento para calcular la integral

${\displaystyle \begin{array}{l}{\left(\frac{dr}{dt}\right)}^2=v_0^2-2GM\left(\frac{1}{R}-\frac{1}{r}\right)\\ t={\displaystyle \underset{R}{\overset{r}{\int }}\sqrt{\frac{rR}{a+br}}dr}\{\begin{array}{l}a=2GMR\\ b=R{v}_0^2-2GM\end{array}\end{array}}$

Se hace un cambio de variable, se integra por partes y finalmente, una fracción racional sencilla

${\displaystyle \begin{array}{l}{x}^2=\frac{r}{a+br}dr=\frac{2ax}{{\left(1-b{x}^2\right)}^2}dx\\ t=\sqrt{R}{\displaystyle \underset{x_1}{\overset{x_2}{\int }}x\frac{2ax}{{\left(1-b{x}^2\right)}^2}}dx=\sqrt{R}{\left(\frac{ax}{b\left(1-b{x}^2\right)}-\frac{a}{2b\sqrt{b}}\log \left(\frac{1+\sqrt{b}x}{1-\sqrt{b}x}\right)\right)|}_{x_1}^{x_2}=\\ \sqrt{R}{\left(\frac{\sqrt{r}\sqrt{a+br}}{b}-\frac{a}{2b\sqrt{b}}\log \left(\frac{\sqrt{a+br}+\sqrt{br}}{\sqrt{a+br}-\sqrt{br}}\right)\right)|}_R^r\end{array}}$

Disparamos un proyectil de masa m desde la superficie de la Tierra con velocidad v₀=1.1·v_e, calcula la velocidad del proyectil cuando se encuentra a una distancia r_s=5·R del centro de la Tierra y el tiempo t que tarda en alcanzar esta posición.

GM=6.67e-11*5.98e24;
R=6.37e6; %radio de la Tierra
ve=sqrt(2*GM/R); %velocidad de escape
v0=1.1*ve; %velocidad de disparo del proyectil
rS=5*R;    
v=sqrt(v0^2-2*GM*(1/R-1/rS));
a=2*GM*R;
b=R*v0^2-2*GM;
t=sqrt(R)*(sqrt(rS)*sqrt(a+b*rS)/b-a*log((sqrt(a+b*rS)+sqrt(b*rS))
/(sqrt(a+b*rS)-sqrt(b*rS)))/(2*b^(3/2))-sqrt(R)*sqrt(a+b*R)/b+
a*log((sqrt(a+b*R)+sqrt(b*R))/(sqrt(a+b*R)-sqrt(b*R)))/(2*b^(3/2)));
fprintf('La velocidad es %3.2f m/s, y el tiempo %3.2f min\n',v,t/60);

La velocidad es 7165.57 m/s, y el tiempo 50.07 min

La velocidad del proyectil ha disminuido a 0.64·v_e

Ecuación del movimiento

Para determinar la posición r del proyectil en función del tiempo t, resolvemos la ecuación diferencial del movimiento por procedimientos numéricos.

${\displaystyle \frac{d^{2}r}{d{t}^2}=-G\frac{M}{r^2}}$

con las siguientes condiciones iniciales: en el instante t=0, r=R, dr/dt=v₀

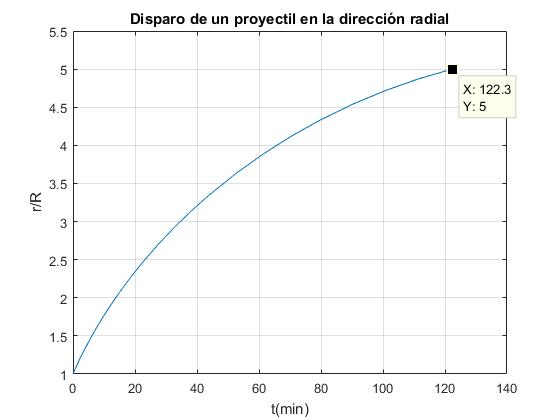
• Disparamos un proyectil de masa m desde la superficie de la Tierra con velocidad v₀=0.9·v_e, determinar la posición r del proyectil en función del tiempo t hasta que regresa a la superficie de la Tierra

GM=6.67e-11*5.98e24;
R=6.37e6; %radio de la Tierra
ve=sqrt(2*GM/R); %velocidad de escape
v0=0.9*ve; %velocidad de disparo del proyectil

x0=[R,v0];
f=@(t,x) [x(2);-GM/x(1)^2]; 
opts=odeset('events',@stop_derribo);

tspan=[0 500*60];
[t,x]=ode45(f,tspan,x0,opts);
plot(t/60,x(:,1)/R)
grid on
xlabel('t(min)')
ylabel('r/R')
title('Disparo de un proyectil en la dirección radial')

Definimos una función para que el proceso de cálculo se detenga cuando el proyectil regrese a la superficie de la Tierra

function [detect,stopin,direction]=stop_derribo(t,x)
    detect=x(1)-6.37e6; 
    stopin=1; 
    direction=-1; 
end



• Disparamos un proyectil de masa m desde la superficie de la Tierra con velocidad v₀=0.9·v_e, determinar la posición r del proyectil en función del tiempo t hasta que se encuentra a una distancia r_s=5·R del centro de la Tierra

Modificamos la definición de la función para que el proceso de cálculo se detenga cuando el proyectil alcance la posición r_s=5·R en el viaje de ida

function [detect,stopin,direction]=stop_derribo(t,x)
    detect=x(1)-5*6.37e6; 
    stopin=1; 
    direction=1; 
end

Choque del proyectil con el satélite

El proyectil y el satélite ambos de la misma masa m, experimentan un choque inelástico quedando pegados ambos cuerpos después del choque.

Aplicamos el principio de conservación del momento lineal para calcular el vector velocidad del objeto resultante de masa 2m tras el choque.

${\displaystyle m{v}_p\widehat{i}+m{v}_s\widehat{j}=2m\overrightarrow{v}}$

Las componentes de la velocidad después del choque son v_x=v_p/2 y v_y=v_s/2

El momento angular y la energ&icaute;a son

${\displaystyle \begin{array}{l}L=(2m)r_s{v}_y=m{r}_s{v}_s\\ E=\frac{1}{2}(2m)\left(v_x^2+v_y^2\right)-G\frac{M(2m)}{r_s}=\frac{1}{4}m\left(v_p^2+v_s^2\right)-2G\frac{Mm}{r_s}\end{array}}$

La ecuación de la trayectoria en coordenadas polares es

${\displaystyle r=\frac{d}{1+\epsilon \cos \left(\theta -{\theta }_0\right)},\epsilon =\sqrt{1+\frac{2L^{2}E}{G^2{M}_s^2{(2m)}^3}},d=\frac{L^2}{G{M}_s{(2m)}^2}}$

La ecuación de la trayectoria es independiente de la masa de la partícula

Si la energía de la partícula es negativa E<0, su trayectoria es una elipse y su excentricidad ε<1.

Conocido d y ε,  se calcula el semieje mayor a, que es la media aritmética de los radios mínimo (θ=0)  y máximo (θ=π) de la elipse.

${\displaystyle 2a=\frac{d}{1+\epsilon }+\frac{d}{1-\epsilon }}$

El periodo viene dado por la fórmula

${\displaystyle P^2=\frac{4{\pi }^2{a}^3}{GM}}$

Trayectoria

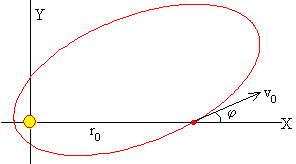
Para representar la trayectoria de un elipse girada es más conveniente utilizar esta ecuación

${\displaystyle \begin{array}{l}\frac{r_0}{r}=-\frac{\cos \phi }{\sin \phi }\sin \theta +\cos \theta +\frac{p(1-\cos \theta )}{2{\sin }^2\phi }\\ p=\frac{2GM}{r_0{v}_0^2}\end{array}}$

p es un parámetro adimensional

Disparamos un proyectil de masa m desde la superficie de la Tierra con velocidad v₀=0.98·v_e, determinar la trayectoria del proyectil después de chocar con un satélite de la misma masa que describe una órbita circular de radio r_s=10·R

GM=6.67e-11*5.98e24;
R=6.37e6; %radio de la Tierra
ve=sqrt(2*GM/R); %velocidad de escape
v0=0.98*ve; %velocidad de disparo del proyectil
rS=10*R; %satélite
vS=sqrt(GM/rS);
rM=2*GM*R/(2*GM-R*v0^2); %máximo alejamiento del centro de la Tierra
if rM>rS || v0>ve
    vP=sqrt(v0^2-2*GM*(1/R-1/rS));
    vX=vP/2; %después del choque
    vY=vS/2;
%trayectoria
    L=rS*vY;
    E=(vX^2+vY^2)/2-GM/rS;
    ex=sqrt(1+2*L^2*E/GM^2); %excentricidad
    d=L^2/GM; %parámetro d de la elipse
    a=d/(1-ex^2);  %semieje mayor
    fprintf('La distancia m&icaute;nima es %1.2f y la máxima %1.2f al centro de 
la Tierra\n',d/(R*(1+ex)), d/(R*(1-ex)))
    P=2*pi*sqrt((a^3/GM)/(24*3600));  %periodo en d&icaute;as
    fprintf('excentricidad %1.3f, periodo d&icaute;as %3.1f\n',ex,P)
    v0=sqrt(vX^2+vY^2);
    phi=atan2(vY,vX);
    p=2*GM/(rS*v0^2);
    r=@(x) (rS/R)./(-cos(phi)*sin(x)/sin(phi)+cos(x)+p*(1-cos(x))/(2*sin(phi)^2));
    hold on
    fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[0,2*pi])
    %punto de lanzamiento
    plot(rS/R,0,'ko', 'markersize',4,'markerfacecolor','k')
    %vector velocidad inicial, en unidades de la velocidad vS por dos
    quiver(rS/R,0, 2*v0*cos(phi)/vS, 2*v0*sin(phi)/vS, 'color','k')

    %eje mayor de la elipse
    th_0=-acos((d/rS-r0)/(r0*ex));
    x1=r(th_0)*cos(th_0);
    y1=r(th_0)*sin(th_0);
    x2=r(th_0+pi)*cos(th_0+pi);
    y2=r(th_0+pi)*sin(th_0+pi);
    line([x1,x2],[y1,y2])
    %la Tierra
    th=(0:360)*pi/180;
    fill(cos(th),sin(th),'b')
    hold off
    axis equal
    xlabel('x')
    ylabel('y')
    grid on
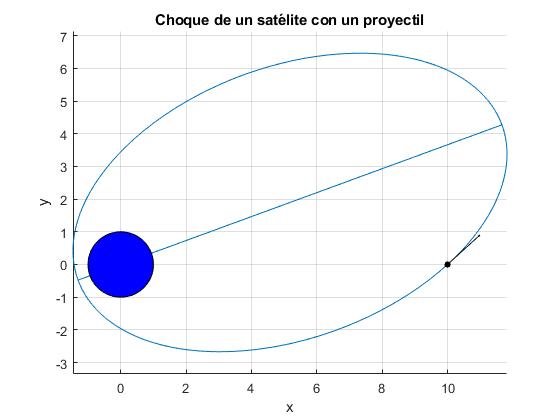
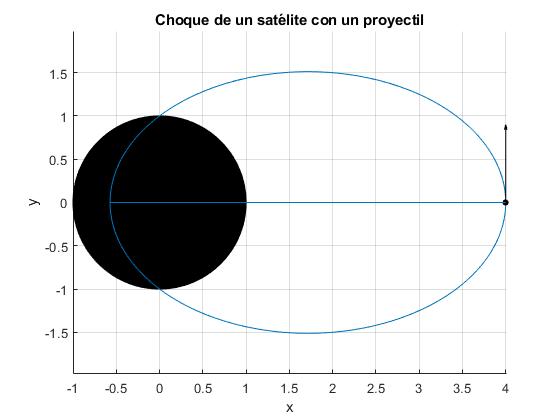
    title('Choque de un satélite con un proyectil')
end

La distancia mínima del objeto resultante del choque entre el proyectil y el satélite al centro de la Tierra es 1.39·R.

La distancia mínima es 1.39 y la máxima 12.42 al centro de la Tierra
excentricidad 0.799, periodo d&icaute;as 312.3

La flecha de color negro muestra la dirección de la velocidad del cuerpo resultante después del choque

Caso particular

Supongamos que el proyectil llega al satélite con velocidad nula v_p=0 y queda pegado. Para que esto ocurra, tenemos que disparar el proyectil desde la superficie de la Tierra con velocidad

${\displaystyle v_0=\sqrt{2GM\left(\frac{1}{R}-\frac{1}{r_s}\right)}}$

Aplicando el principio de conservación del momento lineal al choque entre el proyectil de masa m y velocidad cero, con el satélite de masa m y velocidad v_s, la velocidad del objeto resultante de masa 2m es v_s/2 en la misma dirección

La trayectoria del objeto resultante es una elipse cuyo perigeo calculamos a partir de las propiedades de la fuerza de atracción: central y conservativa

${\displaystyle \begin{array}{l}{r}_s\frac{v_s}{2}=rv\\ \frac{1}{2}{\left(\frac{v_s}{2}\right)}^2-\frac{GM}{r_s}=\frac{1}{2}{v}^2-\frac{GM}{r}\end{array}}$

Conocida la velocidad del satélite v_s en su órbita circular obtenemos la ecuación de segundo grado

${\displaystyle r_s^2-8r·r_s+7r^2=0}$

Conocido r_s calculamos el perigeo r. El valor de r_s que hace que el objeto resultante caiga a la superficie r=R de la Tierra es r_s=7R. Comprobamos que si r_s<7R impacta en la superficie de la Tierra r<R. Por ejemplo, para r_s=4R, obtenemos que r=4R/7

GM=6.67e-11*5.98e24;
R=6.37e6; %radio de la Tierra
rS=4*R; %satélite
vS=sqrt(GM/rS);
vX=0; %después del choque
vY=vS/2;
%trayectoria
L=rS*vY;
E=(vX^2+vY^2)/2-GM/rS;
ex=sqrt(1+2*L^2*E/GM^2); %excentricidad
d=L^2/GM; %parámetro d de la elipse
a=d/(1-ex^2);  %semieje mayor
fprintf('La distancia m&icaute;nima es %1.2f y la máxima %1.2f al centro de la 
Tierra\n',d/(R*(1+ex)), d/(R*(1-ex)))
P=2*pi*sqrt((a^3/GM)/(24*3600));  %periodo en d&icaute;as
fprintf('excentricidad %1.3f, periodo d&icaute;as %3.1f\n',ex,P)
v0=sqrt(vX^2+vY^2);
phi=atan2(vY,vX);
p=2*GM/(rS*v0^2);
r=@(x) (rS/R)./(-cos(phi)*sin(x)/sin(phi)+cos(x)+p*(1-cos(x))/(2*sin(phi)^2));
hold on
%la Tierra
th=(0:360)*pi/180;
fill(cos(th),sin(th),'k')
fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[0,2*pi])
%punto de lanzamiento
plot(rS/R,0,'ko', 'markersize',4,'markerfacecolor','k')
%vector velocidad inicial, en unidades de la velocidad vS por dos
quiver(rS/R,0, 2*v0*cos(phi)/vS, 2*v0*sin(phi)/vS, 'color','k')
    %eje mayor de la elipse
th_0=-acos((d/rS-r0)/(r0*ex));
x1=r(th_0)*cos(th_0);
y1=r(th_0)*sin(th_0);
x2=r(th_0+pi)*cos(th_0+pi);
y2=r(th_0+pi)*sin(th_0+pi);
line([x1,x2],[y1,y2])
hold off
axis equal
xlabel('x')
ylabel('y')
grid on
title('Choque de un satélite con un proyectil')

El objeto resultante después del choque entre el proyectil y el satélite cae a la superficie de la Tierra, su perigeo es menor que el radio de la Tierra

La distancia mínima es 0.57 y la máxima 4.00 al centro de la Tierra

Actividades

Se introduce

• El radio de la órbita circular del satélite en unidades del radio de la Tierra R, en el control titulado Radio órbita
• La velocidad de disparo del proyectil desde la superficie de la Tierra, v₀, en unidades de la velocidad de escape v_e, en el control titulado Velocidad disparo

Se pulsa el botón titulado Nuevo

Observamos el movimiento del satélite en órbita circular de radio r_s y el proyectil disparado desde la superficie de la Tierra con velocidad v₀.

Puede ocurrir que la velocidad de disparo no sea suficiente para que el proyectil llegue a la órbita del satélite. El proyectil regresa a la superficie de la Tierra

Si la velocidad de disparo es suficiente. El proyectil choca con el satélite y se observa la trayectoria del objeto resultante. Si el perigeo es menor que el radio de la Tierra, el objeto se detiene cuando impacta en su superficie, el satélite ha sido derribado por el proyectil

Para que el proyectil llegue con velocidad nula a la órbita del satélite es preciso calcular la velocidad de disparo v₀ aplicando la conservación de la energía y después, introducirla en el control titulado Velocidad disparo en unidades de la velocidad de escape

${\displaystyle \frac{v_0}{v_e}=\sqrt{\left(1-\frac{R}{r_s}\right)}}$

Por ejemplo, si r_s=6·R, entonces v₀/v_e=0.913, para que el proyectil llegue justo a la órbita del satélite y se pegue a éste.

El programa interactivo nos permite jugar a derribar un satélite artificial que describe una órbita circular mediante un proyectil disparado desde la superficie de la Tierra en dirección radial

Ejercicio

Un satélite de masa m describe una órbita circular de radio r_s alrededor de un planeta de masa M y radio R. Un asteroide de la misma masa m, se mueve radialmente partiendo del reposo a grandes distancias del planeta. El satélite y el asteroide chocan inelásticamente y quedan pegados uno al otro.

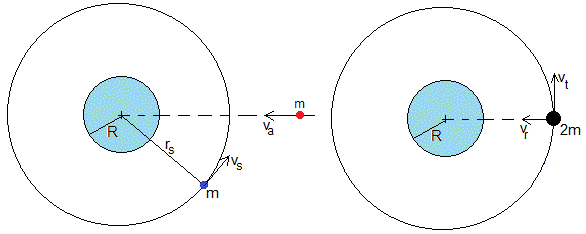
Después del choque el cuerpo resultante describe una órbita elíptica cuyo mínima distancia al centro del planeta es R, vuela rozando la superficie del planeta. Determinar el radio r_s de la órbita del satélite.

• Antes del choque

El satélite describe una órbita circular. De la dinámica del movimiento circular uniforme

${\displaystyle m\frac{v_s^2}{r_s}=G\frac{Mm}{r^2},v_s=\sqrt{\frac{GM}{r_s}}}$

El asteroide parte del infinito con velocidad nula, moviéndose radialmente hacia el planeta. La velocidad del asteroide cuando llega a la órbita del satélite, aplicando la conservación de la energía, es

${\displaystyle \frac{1}{2}m{v}_a^2-G\frac{Mm}{r_s}=\mathrm{0,}{v}_a=\sqrt{2\frac{GM}{r_s}}}$

• Después del choque

Después del choque inelástico, la velocidad del cuerpo resultante de masa 2m tiene dos componentes, en la dirección radial v_r y en la dirección tangencial v_t

En el momento del choque se conserva el momento lineal

• a lo largo de la dirección radial

${\displaystyle m{v}_a=\left(2m\right)v_r,v_r=\frac{1}{2}\sqrt{2\frac{GM}{r_s}}}$

• a lo largo de la dirección tangencial

${\displaystyle m{v}_s=\left(2m\right)v_t,v_t=\frac{1}{2}\sqrt{\frac{GM}{r_s}}}$

El momento angular y la energía del cuerpo resultante son

${\displaystyle \begin{array}{l}L=(2m)r_s{v}_t=m\sqrt{GM{r}_s}\\ E=\frac{1}{2}(2m)\left(v_t^2+v_r^2\right)-G\frac{2mM}{r_s}=-\frac{5}{4}G\frac{mM}{r_s}\end{array}}$

determinan la trayectoria elíptica del cuerpo de masa 2m alrededor del planeta.

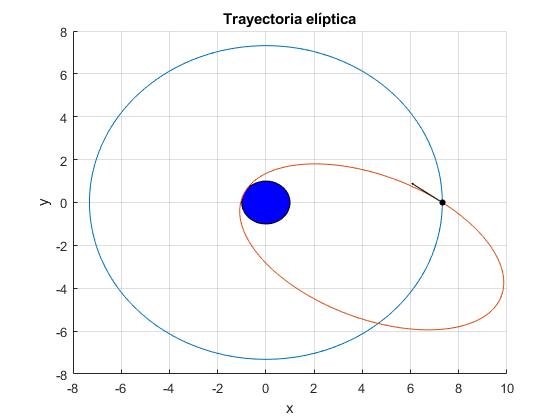
Trayectoria elíptica

La distancia de máximo acercamiento al planeta es R. La energía y el momento angular en esta posición es

${\displaystyle \begin{array}{l}L=(2m)R{v}_R\\ E=\frac{1}{2}(2m)v_R^2-G\frac{2mM}{R}\end{array}}$

En este sistema de dos ecuaciones despejamos r_s y v_R. La incógnita que nos interesa r_s, se despeja de la ecuación de segundo grado

${\displaystyle \begin{array}{l}\frac{r_s}{4R^2}-\frac{2}{R}=-\frac{5}{4}\frac{1}{r_s}\\ r_s=\left(4\pm \sqrt{11}\right)R\end{array}}$

La raíz válida es la positiva, r_s=7.317R. La otra se encuentra en el interior del planeta

La ecuación de la trayectoria en coordenadas polares es

${\displaystyle r=\frac{d}{1+\epsilon \cos \left(\theta -{\theta }_0\right)},\epsilon =\sqrt{1+\frac{2L^{2}E}{G^2{M}^2{(2m)}^3}},d=\frac{L^2}{GM{(2m)}^2}}$

Con el dato de r_s, la energía E y el momento angular L

${\displaystyle \epsilon =\frac{\sqrt{11}}{4}=\mathrm{0.829,}d=\frac{r_s}{4}=\frac{4+\sqrt{11}}{4}R=1.829R}$

La posición de máximo acercamiento es

${\displaystyle r_{mín}=\frac{d}{1+\epsilon }=\frac{\frac{4+\sqrt{11}}{4}R}{1+\frac{\sqrt{11}}{4}}=R}$

La posición más alejada es

${\displaystyle r_{máx}=\frac{d}{1-\epsilon }=\frac{\frac{4+\sqrt{11}}{4}R}{1-\frac{\sqrt{11}}{4}}=\frac{4+\sqrt{11}}{4-\sqrt{11}}R=10.71R}$

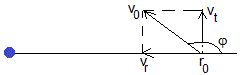
Para representar la trayectoria elíptica girada utilizamos la ecuación

${\displaystyle \begin{array}{l}\frac{r_0}{r}=-\frac{\cos \phi }{\sin \phi }\sin \theta +\cos \theta +\frac{p(1-\cos \theta )}{2{\sin }^2\phi }\\ p=\frac{2GM}{r_0{v}_0^2}\end{array}}$

Donde r₀=r_s, el ángulo φ y el parámetro p valen

${\displaystyle \begin{array}{l}\phi =\pi -\arctan \left(\frac{v_t}{v_r}\right)=\pi -\arctan \left(\frac{1}{\sqrt{2}}\right)\\ p=\frac{8}{3}\end{array}}$

r0=4+sqrt(11); %posición inicial
phi=pi-atan(1/sqrt(2)); %ángulo de tiro
p=8/3; %parámetro adimensional
hold on
th=(0:360)*pi/180;
x1=cos(th); y1=sin(th);
fill(x1,y1,'b')
rs=4+sqrt(11);
fplot(@(x) rs*cos(x),@(x) rs*sin(x),[0,2*pi])
r=@(x) r0./(-cos(phi)*sin(x)/sin(phi)+cos(x)+p*(1-cos(x))/(2*sin(phi)^2));
fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[0,2*pi])
%punto de lanzamiento
plot(r0,0,'ko', 'markersize',4,'markerfacecolor','k')
%vector velocidad inicial, en unidades de vs por dos
quiver(r0,0, 2*sqrt(2/p)*cos(phi), 2*sqrt(2/p)*sin(phi), 'color','k')
hold off
xlabel('x')
ylabel('y')
grid on
title('Trayectoria elíptica')

La flecha de color negro señala la dirección de la velocidad en el punto de impacto

Referencias

Philip R Blanco, Carl E Mungan. Satellite splat: an inelastic collision with a surface-launched projectile. Eur. J. Phys. 36 (2015) 045004.

Este artículo está disponible en la dirección: https://www.usna.edu/Users/physics/mungan/_files/documents/Publications/EJP17.pdf

Physics Challenge for Teachers and Students. Hit and miss. Phys. Teach. 53, January 2015. pp. 59