La energía de una partícula en un campo de fuerzas centrales descrito por un potencial V(r) se expresan en coordenadas polares

${\displaystyle \begin{array}{l}E=\frac{1}{2}m{v}^2+V(r)\hfill \\ E=\frac{1}{2}m{\left(\frac{dr}{dt}\right)}^2+\frac{1}{2}m{r}^2{\left(\frac{d\theta }{dt}\right)}^2+V(r)\hfill \end{array}}$

El momento angular se expresa

${\displaystyle L=m{r}^2\frac{d\theta }{dt}}$

Combinando ambas expresiones

${\displaystyle E=\frac{1}{2}m{\left(\frac{dr}{dt}\right)}^2+\frac{L^2}{2m{r}^2}+V(r)}$

Se denomina potencial efectivo a la suma de los dos últimos términos que dependen de la distancia radial r

${\displaystyle V_{ef}(r)=\frac{L^2}{2m{r}^2}+V(r)}$

Cuando V(r)=-GMm/r encontramos que

• Una partícula con energía E>0, se puede mover desde (r_m,∞). Siendo r_m la raíz positiva de la ecuación

${\displaystyle E=\frac{L^2}{2m{r}^2}+V(r)}$

En las posiciones de retorno, r_m, la componente radial de la velocidad es nula dr/dt=0

• Una partícula con energía E<0, se puede mover en una región (r₁,r₂). Siendo r₁ y r₂ las raices positivas de dicha ecuación

Potencial de Yukawa

El potencial de Yukawa depende de la distancia radial r de la forma

${\displaystyle V(r)=-\frac{k}{r}\exp \left(-\frac{r}{\lambda }\right)}$

El potencial efectivo es

${\displaystyle V_{ef}(r)=-\frac{k}{r}\exp \left(-\frac{r}{\lambda }\right)+\frac{L^2}{2m{r}^2},r\ge 0}$

Definimos la distancia adimensional, x=r/λ

${\displaystyle V_{ef}(x)=\frac{k}{\lambda }\left(-\frac{e^{-x}}{x}+\frac{1}{2\alpha x^2}\right),\alpha =\frac{mk}{L^2}\lambda }$

Estudiamos la función dependiente de la variable x definida entre paréntesis

${\displaystyle y=-\frac{e^{-x}}{x}+\frac{1}{2\alpha x^2}}$

Parámetro α=0.9

Representamos la función y(x) para el valor del parámetro α=0.9

a=0.9; %parámetro alfa
f=@(x) -exp(-x)./x+1./(2*a*x.^2);
fplot(f,[0.5,5])
E=0.2; %energía
g=@(x) f(x)-E;
xm=fzero(g,[0.5,2]); %distancia mínima
line([xm,5],[E,E],'color','k')
line([xm,xm],[0,E],'lineStyle','--','color','k')
ylim([0,0.5])
grid on
xlabel('x')
ylabel('y')
title('Potencial de Yukawa')

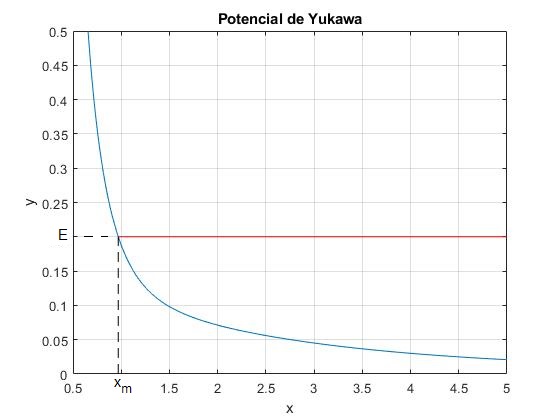
La función V_ef(r) es similar a la de un campo de fuerzas repulsivo inversamente proporcional al cuadrado de la distancia

Cuando la energía de la partícula es E=0.2, la intesección de la recta horizontal y la función energía potencial efectiva, define la distancia de máximo acercamiento x_m al centro de fuerzas

La ecuación E=y(x) es transcendente por lo que utilizamos la función fzero de MATLAB para calcularla

...
f=@(x) -exp(-x)./x+1./(2*a*x.^2);
E=0.2; %energía
g=@(x) f(x)-E;
xm=fzero(g,[0.5,2]); %distancia mínima
...

>> xm
xm =    0.9692

Parámetro α=1.3

Representamos la función y(x) para el valor del parámetro α=1.3

a=1.3; %parámetro
f=@(x) -exp(-x)./x+1./(2*a*x.^2);
hold on
fplot(f,[0.5,5])
g=@(x) x*(x+1)*a-exp(x);
x_min=fzero(g,1);
plot(x_min,f(x_min),'ro','markersize',3,'markeredgecolor','r',
'markerfacecolor','r')
x_max=fzero(g,2);
plot(x_max,f(x_max),'bo','markersize',3,'markeredgecolor','b',
'markerfacecolor','b')

E=0.04; %energía
h=@(x) f(x)-E;
x0=fzero(h,[0.5,x_min]); %distancia mínima
line([x0,5],[E,E],'color','r')
line([x0,x0],[0,f(x0)],'lineStyle','--','color','k')

E=0.02; %energía
h=@(x) f(x)-E;
x1=fzero(h,[0.5,x_min]); %distancia mínima
x2=fzero(h,[x_min,x_max]); %distancia máxima
x3=fzero(h,[x_max,5]); %distancia mínima
line([x1,x2],[E,E],'color','r')
line([x3,5],[E,E],'color','r')
line([x1,x1],[0,f(x1)],'lineStyle','--','color','k')
line([x2,x2],[0,f(x2)],'lineStyle','--','color','k')
line([x3,x3],[0,f(x3)],'lineStyle','--','color','k')
ylim([0,0.05])
hold off
grid on
xlabel('x')
ylabel('y')
title('Potencial de Yukawa')

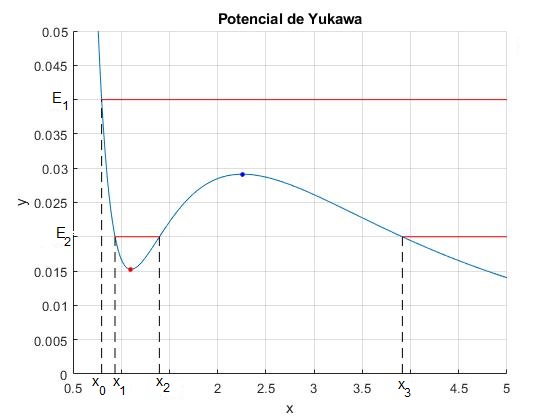
Observamos que la función y(x) presenta un mínimo y un máximo, puntos de color rojo y azul

El extremo de una función se calcula haciendo que su derivada primera sea nula

${\displaystyle \frac{dy}{dx}=\mathrm{0,}\frac{x{e}^{-x}+e^{-x}}{x^2}-\frac{1}{\alpha x^3}=\mathrm{0,}x(x+1)\alpha -e^x=0}$

El mínimo está cerca de x=1 y el máximo está cerca de x=2, ambos los calculamos con fzero de MATLAB

...
g=@(x) x*(x+1)*a-exp(x);
x_min=fzero(g,1);
x_max=fzero(g,2);
...

>> x_min,x_max
x_min =    1.1010
x_max =    2.2578
>> f(x_min)
ans =    0.0153
>> f(x_max)
ans =    0.0291

La derivada segunda de y(x) es

${\displaystyle \frac{d^{2}y}{d{x}^2}=-\frac{x^2+2x+2}{x^3}{e}^{-x}+3\frac{1}{\alpha x^4}}$

Comprobamos que en un mínimo d²y/dx²>0 y que en un máximo d²y/dx²<0

>> h=@(x) -(x^2+2+x*2)*exp(-x)/x^3+3/(a*x^4);
>> h(x_min)
ans =    0.2214
>> h(x_max)
ans =   -0.0167

Para la energía E₁=0.04, la recta horizontal E₁=0.04 y la función y(x) se cortan en un punto que define la distancia mínima x₀ al centro de fuerzas. La partícula se puede mover en el intervalo (x₀, ∞)

...
f=@(x) -exp(-x)./x+1./(2*a*x.^2);
E=0.04; %energía
h=@(x) f(x)-E;
x0=fzero(h,[0.5,x_min]); %distancia mínima
...

>> x0
x0 =    0.7971

El caso más interesante se presenta cuando la energía E₂ está entre la altura del mínimo, 0.0153 y la del máximo, 0.0291, por ejemplo, E₂=0.02

Para esta energía, la recta horizontal E₂=0.02 y la función y(x) se cortan en tres puntos: x₁ situado en el intervalo (0, x_mín), x₂ situado en el intervalo (x_mín, x_máx) y x₃ situado en el intervalo (x_máx, ∞). La partícula se puede mover en el intervalo (x₁, x₂) o en el intervalo (x₃,∞)

...
f=@(x) -exp(-x)./x+1./(2*a*x.^2);
E=0.02; %energía
h=@(x) f(x)-E;
x1=fzero(h,[0.5,x_min]); %distancia mínima
x2=fzero(h,[x_min,x_max]); %distancia máxima
x3=fzero(h,[x_max,5]); %distancia mínima
...

>> x1,x2,x3
x1 =    0.9360
x2 =    1.3958
x3 =    3.9150

Podríamos estar interesados en que el mínimo de y(x) fuese cero, para calcular el valor del parámetro α, hacemos que y(x)=0 y su derivada dy/dx=0 sean nulas simultáneamente

${\displaystyle \{\begin{array}{l}y(x)=\mathrm{0,}-\frac{e^{-x}}{x}+\frac{1}{2\alpha x^2}=\mathrm{0,}{e}^x-2\alpha x=0\\ \frac{dy}{dx}=\mathrm{0,}x(x+1)\alpha -e^x=0\end{array}}$

La solución es x=1, a=e/2=1.3591

Para comprobarlo, se sugiere al lector sustituir en la primera línea de código del script, el valor de α=1.3 por α=1.3591

Punto de inflexión

Hemos comprobado que para α=0.9, no hay máximos y mínimos, para α=1.3 la curva presenta un máximo y un mínimo. Habrá un valor de α para el cual la función y(x) presenta un punto de inflexión, aquél en el que la derivada primera dy/dx=0 y la derivada segunda, d²y/dx²=0, se anulan simultáneamente

${\displaystyle \{\begin{array}{l}\frac{dy}{dx}=\mathrm{0,}x(x+1)\alpha -e^x=0\\ \frac{d^{2}y}{d{x}^2}=\mathrm{0,}x\left(x^2+2x+2\right)-\frac{3}{\alpha }{e}^x=0\end{array}}$

Obtenemos la ecuación x²-x-1=0, cuya raíz positiva es

${\displaystyle \begin{array}{l}x=\frac{1+\sqrt{5}}{2}=1.6180\\ {\alpha }_c=\frac{e^x}{x(x+1)}=1.1905\end{array}}$

hold on
x0=(1+sqrt(5))/2; %punto de inflexión
a=exp(x0)/(x0*(x0+1)); %parámetro
f=@(x) -exp(-x)./x+1./(2*a*x.^2);
fplot(f,[0.5,5])
line([x0,x0],[0,f(x0)],'lineStyle','--','color','k')
line([0,x0],[f(x0),f(x0)],'lineStyle','--','color','k')
plot(x0,f(x0),'ro','markersize',3,'markeredgecolor','r','markerfacecolor','r')
ylim([0,0.1])
hold off
grid on
xlabel('x')
ylabel('y')
title('Potencial de Yukawa')

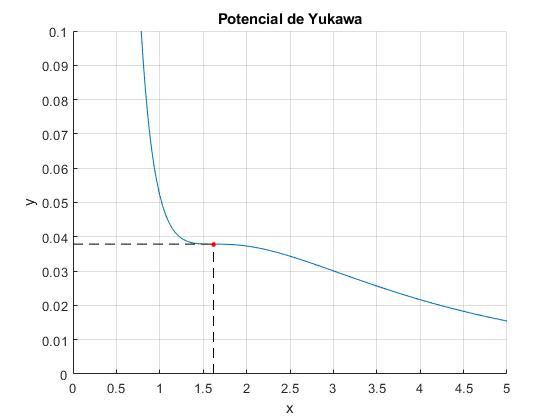
El potencial de Yukawa da lugar a trayectorias cerradas cuando

${\displaystyle \lambda >1.1905\frac{L^2}{mk}}$

Ecuación de la trayectoria

La lagrangiana es

${\displaystyle L=\frac{1}{2}m{\left(\frac{dr}{dt}\right)}^2+\frac{1}{2}m{r}^2{\left(\frac{d\theta }{dt}\right)}^2+\frac{k}{r}\exp \left(-\frac{r}{\lambda }\right)}$

Como la lagrangina no depende de θ, hay una constante del movimiento (el momento angular)

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ \frac{d}{dt}\left(m{r}^2\dot{\theta }\right)=0\\ m{r}^2\frac{d\theta }{dt}=\text{cte}\end{array}}$

La ecuación del movimiento en la dirección radial es

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{r}}\right)-\frac{\partial L}{\partial r}=0\\ m\frac{d^{2}r}{d{t}^2}-mr{\left(\frac{d\theta }{dt}\right)}^2+\frac{k}{r^2}\exp \left(-\frac{r}{\lambda }\right)+\frac{k}{\lambda r}\exp \left(-\frac{r}{\lambda }\right)=0\\ \frac{d^{2}r}{d{t}^2}=\frac{L^2}{m^2{r}^3}-\frac{k}{m\lambda }\left(\frac{\lambda }{r}+1\right)\frac{\exp \left(-\frac{r}{\lambda }\right)}{r}\end{array}}$

Donde L es el momento angular que se mantiene constante. Para calcular la ecuación de la trayectoria, r=r(θ), eliminamos el tiempo t del siguiente modo

${\displaystyle \begin{array}{l}\frac{dr}{dt}=\frac{dr}{d\theta }\frac{d\theta }{dt}=\frac{L}{m{r}^2}\frac{dr}{d\theta }\hfill \\ \frac{d^{2}r}{d{t}^2}=\frac{d}{dt}\left(\frac{L}{m{r}^2}\frac{dr}{d\theta }\right)=\frac{d}{d\theta }\left(\frac{L}{m{r}^2}\frac{dr}{d\theta }\right)\frac{d\theta }{dt}=\frac{L}{m{r}^2}\frac{d}{d\theta }\left(\frac{L}{m{r}^2}\frac{dr}{d\theta }\right)\hfill \\ \frac{d^{2}r}{d{t}^2}=\frac{L^2}{m^2{r}^4}\left(\frac{d^{2}r}{d{\theta }^2}-\frac{2}{r}{\left(\frac{dr}{d\theta }\right)}^2\right)\hfill \end{array}}$

La ecuación diferencial de la trayectoria se escribe

${\displaystyle \frac{L^2}{m^2{r}^4}\left(\frac{d^{2}r}{d{\theta }^2}-\frac{2}{r}{\left(\frac{dr}{d\theta }\right)}^2\right)=\frac{L^2}{m^2{r}^3}-\frac{k}{m\lambda }\left(\frac{\lambda }{r}+1\right)\frac{\exp \left(-\frac{r}{\lambda }\right)}{r}}$

Hacemos el cambio de variable u=1/r

${\displaystyle \begin{array}{l}\frac{dr}{d\theta }=-\frac{1}{u^2}\frac{du}{d\theta }\hfill \\ \frac{d^{2}r}{d{\theta }^2}=\frac{2}{u^3}{\left(\frac{du}{d\theta }\right)}^2-\frac{1}{u^2}\frac{d^{2}u}{d{\theta }^2}\hfill \end{array}}$

La ecuación diferencial de la trayectoria se escribe

${\displaystyle \begin{array}{l}\frac{L^2}{m^2}{u}^4\left(\frac{2}{u^3}{\left(\frac{du}{d\theta }\right)}^2-\frac{1}{u^2}\frac{d^{2}u}{d{\theta }^2}-2u{\left(-\frac{1}{u^2}\frac{du}{d\theta }\right)}^2\right)=\frac{L^2}{m^2}{u}^3-\frac{k}{m\lambda }u\left(\lambda u+1\right)\exp \left(-\frac{1}{\lambda u}\right)\\ \frac{d^2(\lambda u)}{d{\theta }^2}+\lambda u=\alpha \left(\frac{\lambda u+1}{\lambda u}\right)\exp \left(-\frac{1}{\lambda u}\right),\alpha =\frac{mk\lambda }{L^2}\end{array}}$

Energía de la partícula

${\displaystyle \begin{array}{l}E=\frac{1}{2}m\left\{{\left(\frac{dr}{dt}\right)}^2+r^2{\left(\frac{d\theta }{dt}\right)}^2\right\}-\frac{k}{r}\exp \left(-\frac{r}{\lambda }\right)\\ E=\frac{1}{2}\frac{L^2}{m{r}^4}\left\{{\left(\frac{dr}{d\theta }\right)}^2+r^2\right\}-\frac{k}{r}\exp \left(-\frac{r}{\lambda }\right)\end{array}}$

Denominamos x=r/λ

${\displaystyle \begin{array}{l}\frac{E\lambda }{k}=\frac{1}{2}\frac{L^2}{mk\lambda }\left\{\frac{1}{x^4}{\left(\frac{dx}{d\theta }\right)}^2+\frac{1}{x^2}\right\}-\frac{1}{x}\exp \left(-x\right)\\ e=\frac{1}{2\alpha }\left\{\frac{1}{x^4}{\left(\frac{dx}{d\theta }\right)}^2+\frac{1}{x^2}\right\}-\frac{1}{x}\exp \left(-x\right)\end{array}}$

Dada la energía e calculamos la distancia mínima al centro de fuerzas. Por ejemplo, para el valor del parámetro α=1.3, si la energía de la partícula e=0.02, calculamos x₁=0.9360, raíz de la ecuación transcendente con dx/dθ=0

Supongamos que la partícula parte de esa posición x₁=r₁/λ=1/(λu₁)=0.9360. Resolvemos la ecuación diferencial por procedimientos numéricos con las siguientes condiciones iniciales, en la posición (λu₁, θ=0), d(λu)/dθ=0. En el código, denominamos x(1) a (λu) y x(2) a d(λu)/dθ

a=1.3; %parámetro
e=0.02; %energía
h=@(x) 1./(2*a*x.^2)-exp(-x)./x-e;
x1=fzero(h,[0.5,1]); %mímima distancia
f=@(t,x) [x(2); -x(1)+a*(x(1)+1)*exp(-1/x(1))/x(1)]; 
[t,x]=ode45(f,[0,8*pi],[1/x1,0]);
plot(cos(t)./x(:,1), sin(t)./x(:,1))
grid on
axis equal
xlabel('x')
ylabel('y')
title('Potencial de Yukawa')

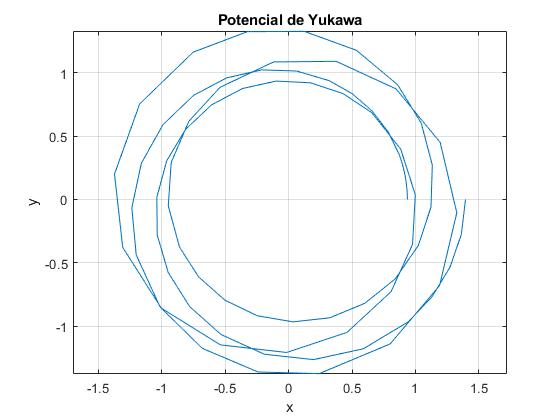
Comprobamos que la mínima distancia es 0.9360 y la máxima 1.3958

>> min(1./x(:,1))
ans =    0.9359
>> max(1./x(:,1))
ans =    1.3956    

Comprobamos que la energía e se mantiene constante e igual a 0.02

>> e=(x(:,2).^2+x(:,1).^2)/(2*a)-x(:,1).*exp(-1./x(:,1))
   e =
    0.0200
    0.0200
    ....
    0.0200
    0.0200

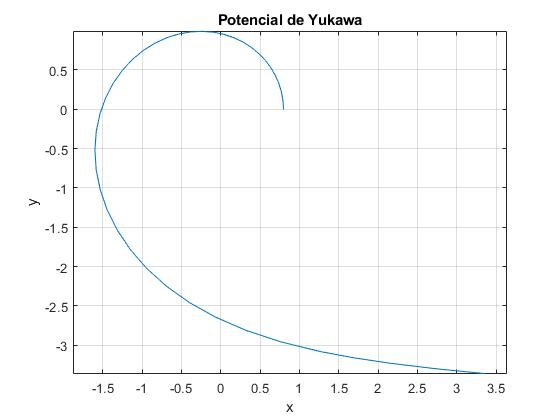
Para el valor del parámetro α=1.3, si la energía de la partícula e=0.04, calculamos la mínima distancia al centro de fuerzas, x₀=0.7971. Resolvemos la ecuación diferencial por procedimientos numéricos con las siguientes condiciones iniciales, en la posición (λu₀=1/x₀, θ=0), d(λu)/dθ=0

a=1.3; %parámetro
e=0.04; %energía
h=@(x) 1./(2*a*x.^2)-exp(-x)./x-e;
x0=fzero(h,[0.5,1]); %mímima distancia
f=@(t,x) [x(2); -x(1)+a*(x(1)+1)*exp(-1/x(1))/x(1)]; 
[t,x]=ode45(f,[0,2*pi-pi/4],[1/x0,0]);
plot(cos(t)./x(:,1), sin(t)./x(:,1))
grid on
axis equal
xlabel('x')
ylabel('y')
title('Potencial de Yukawa')

Referencias

O. L. de Lange, J. Pierrus. Solved Problems in Classical Mechanics. Analytical and numerical solutions with comments. Oxford University Press (2010). Question 8.6, pp. 224-228