Desviación hacia el este de un cuerpo que cae

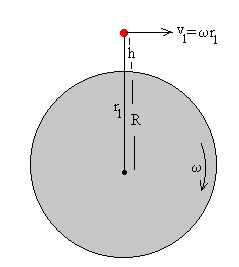
Supongamos un planeta de masa M y radio R, que tiene un movimiento de rotación con velocidad angular ω . Un observador situado en la superficie del planeta ve como cae un cuerpo de masa m desde una altura h por encima del observador.

Para un observador inercial no ligado al movimiento de rotación del planeta, el cuerpo se lanza desde una distancia r=R+h del centro del planeta con una velocidad inicial v₁=ω ·r.

Desde el punto de vista de este observador, el cuerpo se mueve bajo la única influencia de la fuerza de atracción del planeta. Describirá por tanto, una órbita elíptica en uno de cuyos focos estará el centro del planeta. Los pasos de la presente discusión serán los siguientes:

Cálculo de la trayectoria elíptica del cuerpo
Intersección de la trayectoria con la superficie del planeta
Tiempo que tarda en chocar con la superficie
Determinación de su desviación respecto de la dirección radial por el observador no inercial o en rotación con el planeta.

Ecuación de la trayectoria elíptica

La ecuación de una elipse en coordenadas polares es

$r = \frac{d}{1 + ε \cos θ}$

Los valores del parámetro d y de la excentricidad ε se calculan a partir de la energía E y del momento angular L de la partícula

$\begin{array}{l} E = \frac{1}{2} m v_{1}^{2} - \frac{G M m}{r_{1}} \\ L = m v_{1} r_{1} \end{array}$

Ejemplo: Consideremos el planeta Tierra con los siguientes datos

Masa M=5.98·10²⁴ kg
Radio R=6.378·10⁶ m
Velocidad angular de rotación ω =2π /(24·60·60) rad/s
Constante de la gravitación G=6.67·10^-11 Nm²/kg²

Supongamos que el cuerpo se deja caer desde una altura h=0.1·R=637.8 km o bien, desde una distancia r₁=7.02·10⁶ m,

Su velocidad es v₁=ω ·r₁=510.2 m/s.
Su momento angular vale L=3.58·10⁹· m kgm²/s.
Su energía total será E=-5.67·10⁷·m J

Los parámetros d y ε de la trayectoria se obtienen mediante las fórmulas

$\begin{array}{l} d = \frac{L^{2}}{G M m^{2}} = 32122.8 m \\ ε = \sqrt{1 + \frac{2 L^{2} E}{G^{2} M^{2} m^{3}}} = 0.9954 \end{array}$

Conocidos los parámetros d y ε de la ecuación de la trayectoria, se obtiene r₂ y r₁

Cuando θ=0º, r₂=16098 m
Cuando θ=180º, r₁=7.02·10⁶ m

Fuerza central y conservativa

No es necesario utilizar estas dos fórmulas para calcular la ecuación de la trayectoria, existe otro camino alternativo

Conocido r₁ y v₁ se calcula r₂ y v₂ aplicando la constancia del momento angular y de la energía

$\begin{array}{l} m r_{1} \cdot v_{1} = m r_{2} \cdot v_{2} \\ \frac{1}{2} m v_{1}^{2} - \frac{G M m}{r_{1}} = \frac{1}{2} m v_{2}^{2} - \frac{G M m}{r_{2}} \end{array}$

Como en la ecuación de la trayectoria, el valor de r₁ se obtiene para θ =180°, $r_{1} = \frac{d}{1 - ε}$
y el valor de r₂ se obtiene para θ =0°, $r_{2} = \frac{d}{1 + ε}$

De estas dos ecuaciones despejamos d y ε .

Intersección con la superficie del planeta

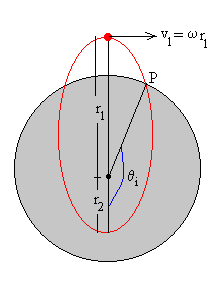
Calculamos la intersección de una elipse y una circunferencia de radio R.

Poniendo en la ecuación de la trayectoria r=R, despejamos el ángulo θ

$\cos θ = \frac{d - R}{ε R}$

Con los datos anteriores cos θ_i=-0.9995, lo que da un ángulo de intersección de θ_i =178.3º.

Tiempo que tarda en chocar con la superficie

Para calcular el tiempo que tarda el cuerpo desde que se deja caer hasta que choca con la superficie del planeta en el punto P, emplearemos la ley de las áreas.

En coordenadas polares el momento angular se expresa

$L = m r^{2} \frac{d θ}{d t}$

Como hemos visto el área barrida por el radio vector entre el instante t y el instante t+dt es un triángulo diferencial de área r²·dθ /2.

El área barrida por el radio vector en el tiempo t es

$A = \int_{0}^{θ} \frac{r^{2} d θ}{2} = \frac{L}{2 m} \int_{0}^{t} d t$

Si calculamos el área A sombreada en color azul claro, obtenemos el tiempo t.

El área A sombreada es la suma del área de un triángulo y el área de la porción de elipse de la figura.

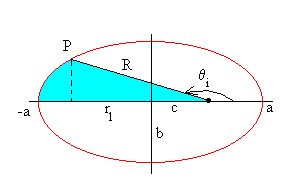
El área del triángulo es

$A_{1} = \frac{R \cdot \cos (π - θ_{i}) \cdot R \sin (π - θ_{i})}{2} = \frac{1}{4} R^{2} \sin (2 (π - θ_{i}))$

El área de la porción de elipse A₂ se puede calcular sumando las áreas de los elementos infinitesimales ydx comprendidos entre x₁=–a y x₂= –R·cos(π -θ_i)+c. Donde a es el semieje mayor de la elipse a=(r₁+r₂)/2, y c es la semidistancia focal c=ε ·a.

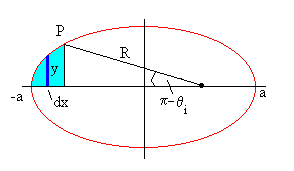
La ecuación de la elipse en coordenadas rectangulares es

$\begin{array}{l} \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 \\ A_{2} = \int_{x_{1}}^{x_{2}} y d x = \int_{x_{1}}^{x_{2}} \frac{1}{b} \sqrt{1 - \frac{x^{2}}{a^{2}}} d x = \frac{a b}{2} {(\arcsin \frac{x}{a} + \frac{x}{a} \sqrt{1 - \frac{x^{2}}{a^{2}}})}_{x_{1}}^{x_{2}} \end{array}$

como x₁=-a, la expresión se reduce a

$A_{2} = \frac{a b}{2} (\frac{π}{2} + \arcsin \frac{x_{2}}{a} + \frac{x_{2}}{a} \sqrt{1 - \frac{x_{2}^{2}}{a^{2}}})$

con x₂= –R·cos(π -θ_i)+ε a

Si x₂=+a obtenemos la mitad del área de la elipse πab/2

Ejemplo:

Siguiendo con los datos anteriores tenemos que

El semieje mayor de la elipse a=(r₁+r₂)/2, vale a=3.52·10⁶ m
La semidistancia focal c=ε ·a, vale c=3.50·10⁶ m
El semieje menor $b = \sqrt{a^{2} - c^{2}}$ , vale b=3.36·10⁵ m

El área A₁=6.17·10¹¹ m²
El área A₂=8.43·10¹⁰ m²
El área total es A=7.0·10¹¹ m²

Solamente nos queda despejar el tiempo de la ecuación

$A = \frac{L}{2 m} t$ , por lo que t=391.6 s

R=6.378e6; %radio Tierra
M=5.98e24; %masa de la Tierra
G=6.67e-11; %constante G

r1=R+0.1*R; %distancia al centro de la Tierra
v1=(2*pi)*r1/(24*60*60); %velocidad
L=r1*v1; %momento angular
d=L^2/(G*M);
E=v1^2/2-G*M/r1; %energía
ex=sqrt(1+2*L^2*E/(G*M)^2); %excentricidad
a=d/(1-ex^2);  %semieje mayor de la elipse
b=a*sqrt(1-ex^2); %semieje menor de la elipse
angulo=acos((d-R)/(R*ex));
area1=R^2*sin(2*(pi-angulo))/4;
x2=-R*cos(pi-angulo)+ex*a;
area2=a*b*(pi/2+asin(x2/a)+x2*sqrt(1-(x2/a)^2)/a)/2;
fprintf('El tiempo de vuelo (s) es %4.1f\n',2*(area1+area2)/L)

El tiempo de vuelo (s) es 391.6

Tiempo de vuelo empleando la ecuación de Kepler

Se calcula el tiempo t₀ para posición angular θ_i
Se calcula el tiempo t₁ para posición π

R=6.378e6; %radio Tierra
M=5.98e24; %masa de la Tierra
G=6.67e-11; %constante G

r1=R+0.1*R; %distancia al centro de la Tierra
v1=(2*pi)*r1/(24*60*60); %velocidad
L=r1*v1; %momento angular
d=L^2/(G*M);
E=v1^2/2-G*M/r1; %energía
ex=sqrt(1+2*L^2*E/(G*M)^2); %excentricidad
a=d/(1-ex^2);  %semieje mayor de la elipse
angulo=acos((d-R)/(R*ex));
th=angulo; %posición inicial
c_E=(ex+cos(th))/(1+ex*cos(th));
s_E=sqrt(1-ex^2)*sin(th)/(1+ex*cos(th));
E=atan2(s_E,c_E);
if E<0
    E=2*pi+E;
end
t0=(E-ex*s_E)*a^(3/2)/sqrt(G*M);
th=pi; %posición final
c_E=(ex+cos(th))/(1+ex*cos(th));
s_E=sqrt(1-ex^2)*sin(th)/(1+ex*cos(th));
E=atan2(s_E,c_E);
if E<0
    E=2*pi+E;
end
t1=(E-ex*s_E)*a^(3/2)/sqrt(G*M);
fprintf('El tiempo de vuelo (s) es %4.1f\n',(t1-t0))

El tiempo de vuelo (s) es 391.6

Determinación de su desviación respecto de la dirección radial por el observador no inercial, o en rotación con el planeta.

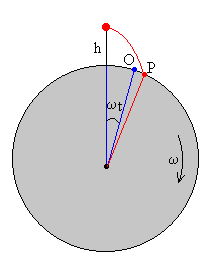
El cuerpo después de un tiempo t choca con la superficie del planeta en P. La posición angular del punto P es π-θ_i. Mientras tanto el observador se ha desplazado al punto O cuya posición angular es ω·t.

La distancia a lo largo de la superficie del planeta entre O y P es la longitud del arco

s=R·(π-θ_i-ω·t)

Con los datos que disponemos s=11837 m

Comparación con la desviación obtenida aplicando la fórmula de la aceleración de Coriolis

Vamos a comparar la desviación hacia el este de un cuerpo que se deja caer desde una altura h en el Ecuador mediante el procedimiento explicado en esta página, con la desviación obtenida aplicando la fórmula de la aceleración de Coriolis.

La fuerza de atracción es central y conservativa. La trayectoria que sigue el cuerpo en su caída es elíptica

Sea h=0.01·R=63780 m. cerca de la superficie de la Tierra

Los datos iniciales necesarios para determinar la trayectoria elíptica son:

r₁=R+h=6.44·10⁶ m
v₁=ω ·r₁=468.5 m/s

De la constancia del momento angular y de la energía obtenemos r₂ y v₂. Solamente nos interesa r₂=11436 m.

El semieje mayor de la elipse vale a=(r₁+r₂)/2=3.35·10⁶ m
La semidistancia focal c=r₁-a=3.09·10⁶ m
La excentricidad ε =c/a=0.996
El semieje menor $b = \sqrt{a^{2} - c^{2}}$ =2.71·10⁵ m

El parámetro d=a(1- e²)=22831.2 m

El ángulo θ_i=179.52º

El área total A=A₁+ A₂=1.715·10¹¹+2.30·10⁹=1.74·10¹¹

El tiempo t que tarda en llegar el móvil a la superficie de la Tierra t=2A/(r₁·v₁)=115.21 s

La desviación del cuerpo respecto del observador en la superficie terrestre.

s=R·(π-θ _i-ω·t)=355.43 m

Caída de un cuerpo descrita por un observador en rotación (no inercial).

Tiempo que tarda en llegar a la superficie de la Tierra cayendo desde una altura de h=63780 m.

Con h=gt²/2, tomando g=9.8, se obtiene t=114.1 s

Aplicando la fórmula de la desviación para la latitud λ =0º.

$s = \frac{1}{3} g ω \cos λ \cdot t^{3} = \frac{1}{3} 9.8 \cdot \frac{2 π}{24 \cdot 60 \cdot 60} \cdot t^{3} = 352.8 m$

Obtenemos un valor muy parecido, a pesar de que g es más pequeño que 9.8 debido a la aceleración centrífuga y a que disminuye con la altura.

Cálculo con MATLAB

R=6.37e6; %radio de la Tierra
M=5.98e24; %masa de la Tierra
G=6.67e-11; %constante G
w=2*pi/(24*3600); %velocidad angular de rotación

r1=(1+0.01)*R; %un cuerpo se deja caer desde una altura de 0.01*R
v1=w*r1;

L=v1*r1; %momento angular
E=v1^2/2-G*M/r1; %energía
ex=sqrt(1+2*L^2*E/(G*M)^2); %excentricidad
d=L^2/(G*M);
a=d/(1-ex^2);  %semieje mayor de la elipse
b=a*sqrt(1-ex^2); %semieje menor
angulo=acos((d-R)/(R*ex));
area1=R^2*sin(2*(pi-angulo))/4;
x2=-R*cos(pi-angulo)+ex*a;
area2=a*b*(pi/2+asin(x2/a)+x2*sqrt(1-(x2/a)^2)/a)/2;
t=2*(area1+area2)/L; %tiempo
alcance=R*(pi-angulo-w*t); %alcance
fprintf('Alcance (m) es %3.1f y tiempo (s) de vuelo %4.1f\n'
,alcance, t)

Alcance (m) es 354.3 y tiempo (s) de vuelo 115.0

Actividades

Se elige un planeta en el control titulado Planeta entre los siguientes:

Planeta	Periodo de rotación (horas)	Radio ecuatorial (km)	Masa × 5.98 10²⁴ kg
Mercurio	1406.4	2 439	0.06
Venus	5 832	6 051	0.82
Tierra	24.0	6 378	1.00
Marte	24.6	3 394	0.11
Júpiter	9.9	71 398	318
Saturno	10.2	60 000	95.1
Urano	10.8	25 400	14.6
Neptuno	15.8	24 750	17.2
Plutón	153.6	1 400	0.002

Fuente: M. Márov. Planetas del Sistema Solar. Editorial Mir

Se introduce la altura sobre la superficie del planeta, una fracción del radio del mismo, en el control titulado Altura

Se pulsa el botón titulado Nuevo.

El objeto que está a una altura h por encima del observador no inercial situado en la superficie del planeta, empieza a caer. Su trayectoria para un observador inercial es una porción de una elipse, al mismo tiempo que el objeto cae el observador no inercial describe un movimiento circular. El observador inercial mide el desplazamiento de ambos durante el tiempo de caída del cuerpo.

El observador no inercial situado en la superficie del planeta mide el desplazamiento relativo del cuerpo, la longitud del arco de circunferencia entre la posición que ocupa el observador (un punto de color rojo) y el punto de impacto del cuerpo sobre la superficie del planeta.

La desviación hacia el este del cuerpo que cae es pequeña para los planetas con velocidad de rotación muy baja como Venus y es muy acusada, para planetas con elevada velocidad angular de rotación como Júpiter.

Planeta:
Altura