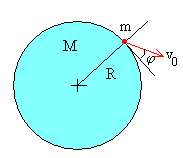
Supondremos que la Tierra está estacionaria en el espacio

El momento angular y la energía de un proyectil de masa m lanzado desde una distancia R del centro de la Tierra, con velocidad v₀ haciendo un ángulo 90-φ con la dirección radial es

${\displaystyle \begin{array}{l}L=mR{v}_0\cos \phi \\ E=\frac{1}{2}m{v}_0^2-\frac{GMm}{R}\end{array}}$

que se mantienen constantes en todos los puntos de la trayectoria.

La ecuación de la trayectoria en coordenadas polares es

${\displaystyle r=\frac{d}{1+\epsilon \cos \theta }\epsilon =\sqrt{1+\frac{2L^{2}E}{G^2{M}^2{m}^3}}d=\frac{L^2}{GM{m}^2}}$

La ecuación de la trayectoria es independiente de la masa m del proyectil.

Si la energía del proyectil es negativa E<0 la trayectoria es una elipse. La velocidad de disparo v₀ debe ser menor que la velocidad de escape v_e

${\displaystyle \frac{1}{2}m{v}_e^2-G\frac{Mm}{R}=0v_e=\sqrt{\frac{2GM}{R}}=11190.7\text{m/s}}$

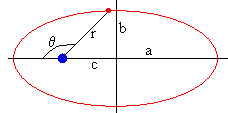
Conocidos d y ε, se calculan

• El semieje mayor a, que es la media aritmética de los radios mínimo (θ=0)  y máximo (θ=π) de la elipse.

${\displaystyle 2a=\frac{d}{1+\epsilon }+\frac{d}{1-\epsilon }a=\frac{d}{1-{\epsilon }^2}}$

• La semidistancia focal c=ε·a

• El semieje menor b de la elipse $b=\sqrt{a^2-c^2}$

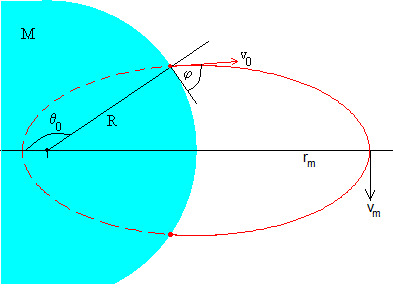
En coordenadas polares, el proyectil sale de la posición R, θ₀, y llega a la posición R, -θ₀, donde

${\displaystyle R=\frac{d}{1+\epsilon \cos {\theta }_0}\cos {\theta }_0=\frac{d-R}{R\epsilon }}$

El alcance del proyectil, es la medida del arco a lo largo de la superficie de la Tierra entre la posición de disparo y la de impacto 2·R·(π-θ₀)

La distancia máxima al centro de la Tierra se calcula en la ecuación de la elipse en coordenadas polares con θ=π.

${\displaystyle r_m=\frac{d}{1-\epsilon }}$

La altura máxima sobre la superficie de la Tierra es h_m=r_m-R

Alternativamente, calculamos la distancia máxima r_m y la velocidad v_m a partir de la constancia del momento angular y de la energía

${\displaystyle \{\begin{array}{l}mR{v}_0\cos \phi =m{r}_m{v}_m\\ \frac{1}{2}m{v}_0^2-\frac{GMm}{R}=\frac{1}{2}m{v}_m^2-\frac{GMm}{r_m}\end{array}}$

Alcance máximo

El alcance es el arco s=2R(π-θ₀) que va de la posición de disparo hasta el impacto.

Para simplificar las expresiones denominamos

${\displaystyle k=\frac{R{v}_0^2}{GM}}$

Como la velocidad de disparo v₀ tiene que ser menor que la de escape v_e, por lo que k<2

Las expresiones del parámetro d, excentricidad ε, son

${\displaystyle \begin{array}{l}d=\frac{L^2}{GM{m}^2}=Rk{\cos }^2\phi \\ \epsilon =\sqrt{1+\frac{2L^{2}E}{G^2{M}^2{m}^3}}=\sqrt{1-k\left(2-k\right){\cos }^2\phi }\end{array}}$

La expresión del arco s es

${\displaystyle \begin{array}{l}s=2R\left(\pi -{\theta }_0\right)\\ s=2R\left(\pi -\arccos \frac{k{\cos }^2\phi -1}{\sqrt{1-k\left(2-k\right){\cos }^2\phi }}\right)=2R\arccos \frac{1-k{\cos }^2\phi }{\sqrt{1-k\left(2-k\right){\cos }^2\phi }}\end{array}}$

Utilizamos MATLAB para calcular el máximo de la función

${\displaystyle f(x)=\arccos \frac{1-k{x}^2}{\sqrt{1-k\left(2-k\right)x^2}}x=\cos \phi }$

>> syms k x;
>> y=acos((1-k*x^2)/sqrt(1+(k^2-2*k)*x^2));
>> solve(diff(y,x))
ans =
  1/(2 - k)^(1/2)
 -1/(2 - k)^(1/2)

El alcance máximo se produce para el ángulo φ_m

${\displaystyle \begin{array}{l}\cos {\phi }_m=\frac{1}{\sqrt{2-k}}\\ s_m=2R\arccos \left(\frac{2\sqrt{1-k}}{(2-k)}\right)\end{array}}$

Para valores de k>1 no hay alcance máximo,

Representamos s/(2R) para varios valores de k

hold on
for k=[0.2,0.5,0.9]
    s=@(x) (acos((1-k*cos(x).^2)./sqrt(1+k*(k-2)*cos(x).^2)));
    fplot(s,[0,pi/2], 'displayName',num2str(k))
end
hold off
legend('-DynamicLegend','location','northeast')
grid on
xlabel('\phi')
ylabel('s')
title('Alcance')

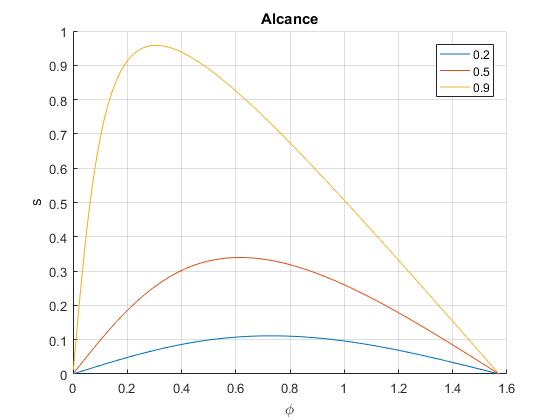
Por ejemplo, para k=0.5, o una velocidad de disparo,v₀=5595 m/s, el ángulo para el cual se produce el alcance máximo es φ_m=0.62 rad (35.3°) como vemos en la gráfica (curva de color rojo). Calculamos este alcance s_m= 4329.5 km

Tiempo de vuelo

Tenemos dos formas de calcular el tiempo de vuelo

• Aplicando la constancia del momento angular, tal como se dedujo el periodo P de un planeta
• La ecuación de Kepler. Dada la posición angular θ del cuerpo celeste determinamos el tiempo t

El momento angular en coordenadas polares se escribe

${\displaystyle L=m{r}^2\frac{d\theta }{dt}}$

Integrando

${\displaystyle {\displaystyle \underset{{\theta }_0}{\overset{\pi }{\int }}\frac{1}{2}{r}^{2}d\theta }={\displaystyle \underset{0}{\overset{t}{\int }}\frac{L}{2m}dt}}$

El primer miembro, es el área barrida por el radio vector cuando el proyectil se mueve desde la posición angular θ=θ₀, a la posición θ=π. El tiempo de vuelo t se obtiene.

${\displaystyle t=2\frac{2m·\text{Area}}{L}}$

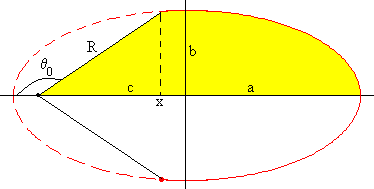
El área sombreada es el área de la porción de elipse comprendida entre x y a más el área del triángulo de base R·cos(π-θ₀) y altura R·sin(π-θ₀), siendo x=-c+R·cos(π-θ₀)

Sabiendo que la ecuación de la elipse es

${\displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2}=1}$  

donde a es el semieje mayor de la elipse, b el semieje menor, y c la semidistancia focal.

El área de la porción de elipse comprendida entre x y a es

${\displaystyle {\displaystyle \underset{x}{\overset{a}{\int }}b\sqrt{1-\frac{x^2}{a^2}}dx}={\displaystyle \underset{z_1}{\overset{z_2}{\int }}ab{\cos }^{2}z·dz}=\frac{ab}{2}{\left[z+\frac{1}{2}\text{sin}2z\right]}_{z_1}^{z_2}=\frac{ab}{2}\left(\frac{\pi }{2}-z_1-\frac{1}{2}\text{sin}2z_1\right)}$

Para integrar, se ha hecho el cambio de variable x=a·sin z. Los nuevos límites de integración son:

• cuando x=a, z₂=π/2,
• cuando -c-R·cosθ₀=a·sinz₁

El área sombreada vale, por tanto

${\displaystyle \text{Area}=\frac{ab}{2}\left(\frac{\pi }{2}-z_1-\frac{1}{2}\text{sin}2z_1\right)-\frac{R^2\text{sin}2{\theta }_0}{4}}$

Caso particular

El ángulo de disparo es φ=90º.

El momento angular L=0, por lo que la trayectoria es una línea recta que pasa por el centro de fuerzas. El proyectil asciende y desciende cayendo hacia la Tierra a lo largo de la dirección radial.

La máxima altura que alcanza, se calcula poniendo v=0 en la ecuación de la energía y se despejando la incógnita r.

${\displaystyle E=\frac{1}{2}m{v}_0^2-\frac{GMm}{R}=-\frac{GMm}{r}}$

En la página titulada Movimiento de dos cuerpos bajo la fuerza de atracción mutua, calculamos el tiempo que tarda el proyectil en volver a la superficie de la Tierra .

Aplicando la ecuación de Kepler

La ecuación de Kepler nos permite calcular la posición de un cuerpo celeste en un instante dado, o bien, el instante t en que el cuerpo celeste se encuentra en una determinada posición θ. En la página titulada El problema de Kepler se proporcionan ejemplos de ambos.

Calculamos el instante t₀ cuando se dispara el proyectil desde la posición θ=θ₀. Después calculamos el instante t₁ cuando el proyectil impacta en la superficie de la Tierra, en la posición θ=2π-θ₀. El procedimiento de cálculo requiere repetir dos veces los pasos:

1. Dada la posición angular θ, determinamos el ángulo E mediante las relaciones

${\displaystyle \sin E=\frac{\sqrt{1-{\epsilon }^2}\sin \theta }{1+\epsilon \cos \theta }\cos E=\frac{\epsilon +\cos \theta }{1+\epsilon \cos \theta }}$

2. Sustituyendo en la ecuación de Kepler, obtenemos M_e

${\displaystyle M_e=E-\epsilon \sin E}$

3. Conocido M_e obtenemos el tiempo

${\displaystyle t=\frac{M_e}{2\pi }P}$

Donde P es el periodo

Una vez que se ha calculado t₀ y t₁. El tiempo de vuelo es la diferencia, T=t₁-t₀

Más adelante, en Ejemplos codificaremos este procedimiento para calcular el tiempo de vuelo

Solución analítica

Vamos a intentar encontrar una expresión analítica del tiempo de vuelo T en función del parámetro k y del ángulo de disparo φ

Dada la posición angular θ, determinamos el ángulo E mediante las relaciones siguientes:

${\displaystyle \begin{array}{l}\sin E=\frac{\sqrt{1-{\epsilon }^2}\sin \theta }{1+\epsilon \cos \theta }\\ \cos E=\frac{\epsilon +\cos \theta }{1+\epsilon \cos \theta }\end{array}}$

La posición de disparo es θ=θ₀. Conocemos la expresión de cosθ₀ y la excentricidad ε en función del parámetro k y el ángulo de disparo φ

${\displaystyle \begin{array}{l}\cos {\theta }_0=\frac{d-R}{\epsilon R}=\frac{1-k{\cos }^2\phi }{\sqrt{1-k\left(2-k\right){\cos }^2\phi }}\\ \epsilon =\sqrt{1+k\left(k-2\right){\cos }^2\phi }\end{array}}$

Dado que

${\displaystyle \sin E_0=\frac{\sqrt{1-{\epsilon }^2}\sqrt{1-{\cos }^2{\theta }_0}}{1+\epsilon \cos {\theta }_0}}$

Operando y simplificando llegamos a la expresión de sinE₀ y cosE₀

${\displaystyle \begin{array}{l}\sin E_0=\frac{\sqrt{k(2-k)}\sin \phi }{\sqrt{1-k\left(2-k\right){\cos }^2\phi }}\\ \cos E_0=\frac{k-1}{\sqrt{1-k\left(2-k\right){\cos }^2\phi }}\end{array}}$

• Cuando k>1, el seno y el coseno son positivos (primer cuadrante). E₀=α

${\displaystyle \alpha =\arcsin \left(\frac{\sqrt{k(2-k)}\sin \phi }{\sqrt{1-k\left(2-k\right){\cos }^2\phi }}\right)}$

• Cuando k≤1, el seno es positivo y el coseno negativo (segundo cuadrante) E₀=π-α

El instante t₀ es

${\displaystyle \begin{array}{l}{t}_0=\frac{E_0-\epsilon \sin E_0}{2\pi }P\\ a=\frac{d}{1-{\epsilon }^2}=\frac{R}{2-k}{P}^2=\frac{4{\pi }^2}{GM}{a}^3\end{array}}$

La posición del punto de impacto es θ=2π-θ₀. Los cosenos son iguales y del mismo signo, cos(θ₀)=cos(2π-θ₀), los senos son de signo contrario sin(θ₀)=-sin(2π-θ₀) por lo que, sinE₁=-sinE₀ y cosE₁=cosE₀

• Cuando k>1, el seno es negativo y el coseno es positivo (cuarto cuadrante). E₁=2π-α

• Cuando k≤1, el seno es negativo y el coseno es negativo (tercer cuadrante). E₁=π+α

El instante t₁ de impacto es

${\displaystyle t_1=\frac{E_1-\epsilon \sin E_1}{2\pi }P}$

La diferencia t₁-t₀ es el tiempo de vuelo

${\displaystyle \begin{array}{l}T=t_1-t_0=\frac{(E_1-E_0)-\epsilon \left(\sin E_1-\sin E_0\right)}{\sqrt{GM}}\sqrt{\frac{R^3}{{(2-k)}^3}}\\ T=\{\begin{array}{l}2\frac{\alpha +\sqrt{k(2-k)}\sin \phi }{\sqrt{GM}}\sqrt{\frac{R^3}{{(2-k)}^3}}k\le 1\\ 2\frac{(\pi -\alpha )+\sqrt{k(2-k)}\sin \phi }{\sqrt{GM}}\sqrt{\frac{R^3}{{(2-k)}^3}}k>1\end{array}\end{array}}$

Ejemplo

Disparamos un proyectil desde algún lugar de la superficie de la Tierra con velocidad inicial v₀= 7500 m/s en la dirección que hace φ=60º con el plano local

La energía del proyectil y el momento angular valen

L=6.37·10⁶·7500·cos60º=2.39 ·10¹⁰ m kgm²/s

${\displaystyle E=\frac{1}{2}m{7500}^2-\frac{6.67·{10}^{-11}·5.98·{10}^{24}m}{6.37·{10}^6}=-34.49·{10}^6·m\text{J}}$

Trayectoria

Conocidos los valores de la energía E y del momento angular L, calculamos el valor del parámetros geométricos de la elipse: d y la excentricidad ε

ε=0.867
d=1.43·10⁶ m

Con estos datos calculamos el ángulo θ₀.

${\displaystyle \cos {\theta }_0=\frac{1.43·{10}^6-6.37·{10}^6}{6.37·{10}^6·0.867}{\theta }_0=153.4º}$

El alcance del proyectil es 2·R·(π-θ₀)= 2·6.37·10⁶·(π-2.68)=5.92·10⁶ m

R=6.37e6; %radio de la Tierra
M=5.98e24; %masa de la Tierra
G=6.67e-11; %constante G

v0=7500; %velocidad de disparo
ang=pi/3; %ángulo de tiro
k=R*v0^2/(G*M);
alcance=2*R*acos((1-k*cos(ang)^2)/sqrt(1+k*(k-2)*cos(ang)^2)); %alcance
fprintf('Alcance (km) es %2.1f\n',alcance/1000)

Alcance (km) es 5923.7

Calculamos la distancia máxima r_m y la velocidad v_m aplicando la constancia del momento angular y de la energía

${\displaystyle \begin{array}{l}{v}_m=\frac{mGM}{L}-\sqrt{{\left(\frac{mGM}{L}\right)}^2+2\frac{E}{m}}\hfill \\ r_m=\frac{L}{m{v}_m}\hfill \end{array}}$

El resultado es v_m=2212 m/s, y r_m=10.80·10⁶ m

Esta distancia se calcula también a partir de la ecuación de la trayectoria para θ=π, r_m=d/(1-ε)=1.43·10⁶/(1-0.867)

Tiempo de vuelo aplicando la constancia del momento angular

Para calcular el tiempo de vuelo tenemos que calcular primero el área barrida por el radio vector desde la posición angular θ=θ₀, a la posición θ=π sombreada de elipse y multiplicarla por dos

En primer lugar, necesitamos los valores de los parámetros de la elipse:

• semieje mayor a=5.78·10⁶ m
• semieje menor b=2.88·10⁶ m

a·sinz₁=-c-R·cosθ₀        z₁=6.73º=0.117 rad

${\displaystyle \text{Area}=\frac{ab}{2}\left(\frac{\pi }{2}-z_1-\frac{1}{2}\text{sin}2z_1\right)-\frac{R^2\text{sin}2{\theta }_0}{4}}$

Area=1.925·10¹³

El tiempo de vuelo es

${\displaystyle t=2\frac{2m·\text{Area}}{L}=3223.1\text{s}}$

R=6.37e6; %radio de la Tierra
M=5.98e24; %masa de la Tierra
G=6.67e-11; %constante G

v0=7500; %velocidad de disparo
ang=pi/3; %ángulo de tiro
L=R*v0*cos(ang); %momento angular
E=v0^2/2-G*M/R; %energía
ex=sqrt(1+2*L^2*E/(G*M)^2); %excentricidad
d=L^2/(G*M);
angulo=acos((d-R)/(R*ex));
alcance=2*R*(pi-angulo); %alcance
fprintf('Alcance (km) es %2.1f\n',alcance/1000)

a=d/(1-ex^2);  %semieje mayor de la elipse
b=a*sqrt(1-ex^2); %semieje menor
z1=asin((-ex*a-R*cos(angulo))/a);
area=a*b*(pi/2-z1-sin(2*z1)/2)/2-R^2*sin(2*angulo)/4;
P=4*area/L; %tiempo de vuelo
fprintf('El tiempo de vuelo (min) es %4.1f\n',P/60)

Alcance (km) es 5923.7
El tiempo de vuelo (min) es 53.7

Tiempo de vuelo aplicando la ecuación de Kepler

Conocidos los valores de la energía E y del momento angular L, calculamos el valor del parámetros geométricos de la elipse: d y la excentricidad ε

Con estos datos calculamos el ángulo θ₀, tal como se ha hecho en el apartado anterior

Conocido el semieje mayor a de la elipse, calculamos el periodo P del proyectil

${\displaystyle a=\frac{d}{1-{\epsilon }^2}{P}^2=\frac{4{\pi }^2}{GM}{a}^3}$

Dada la posición angular θ, determinamos el ángulo E mediante las relaciones

${\displaystyle \sin E=\frac{\sqrt{1-{\epsilon }^2}\sin \theta }{1+\epsilon \cos \theta }\cos E=\frac{\epsilon +\cos \theta }{1+\epsilon \cos \theta }}$

Dependiendo del signo del seno y del coseno, se determina el cuadrante y se calcula el ángulo E. Sustituyendo en la ecuación de Kepler, obtenemos el tiempo t

${\displaystyle t=\frac{E-\epsilon \sin E}{2\pi }P}$

Dada la posición angular θ₁=2π-θ₀ final, determinamos el instante t₁ aplicando las mismas relaciones

Creamos un script para calcular el tiempo de vuelo, T=t₁-t₀

R=6.37e6; %radio de la Tierra
M=5.98e24; %masa de la Tierra
G=6.67e-11; %constante G

v0=7500; %velocidad de disparo
ang=pi/3; %ángulo de tiro
%tiempo de vuelo
L=R*v0*cos(ang); %momento angular
d=L^2/(G*M);
E=v0^2/2-G*M/R; %energía
ex=sqrt(1+2*L^2*E/(G*M)^2); %excentricidad
a=d/(1-ex^2);  %semieje mayor de la elipse
angulo=acos((d-R)/(R*ex));

th=angulo; %posición inicial
c_E=(ex+cos(th))/(1+ex*cos(th));
s_E=sqrt(1-ex^2)*sin(th)/(1+ex*cos(th));
E=atan2(s_E,c_E);
if E<0
    E=2*pi+E;
end
t0=(E-ex*s_E)*a^(3/2)/sqrt(G*M);

th=2*pi-angulo; %impacto en la superficie de la Tierra
c_E=(ex+cos(th))/(1+ex*cos(th));
s_E=sqrt(1-ex^2)*sin(th)/(1+ex*cos(th));
E=atan2(s_E,c_E);
if E<0
    E=2*pi+E;
end
t1=(E-ex*s_E)*a^(3/2)/sqrt(G*M);
fprintf('El tiempo de vuelo (min) es %4.1f\n',(t1-t0)/60)

El tiempo de vuelo (min) es 53.7

Calculamos de forma alternativa, mediante la expresión analítica, el alcance y el tiempo de vuelo y dibujamos la trayectoria

R=6.37e6; %radio de la Tierra
M=5.98e24; %masa de la Tierra
G=6.67e-11; %constante G

v0=7500; %velocidad de disparo
phi=pi/3; %ángulo de tiro
k=R*v0^2/(G*M);
alcance=2*R*acos((1-k*cos(phi)^2)/sqrt(1+k*(k-2)*cos(phi)^2)); %alcance
%tiempo de vuelo
alpha=asin(sqrt(k*(2-k))*sin(phi)/sqrt(1-k*(2-k)*cos(phi)^2));
if k<=1
    T=2*(alpha+sqrt(k*(2-k))*sin(phi))*sqrt((R/(2-k))^3)/sqrt(G*M);
else
     T=2*(pi-alpha+sqrt(k*(2-k))*sin(phi))*sqrt((R/(2-k))^3)/sqrt(G*M);
end 
fprintf('Alcance (km) es %2.1f\n',alcance/1000)
fprintf('El tiempo de vuelo (min) es %4.1f\n',T/60)

%trayectoria
d=k*cos(phi)^2;
ex=sqrt(1-k*(2-k)*cos(phi)^2);
th_0=acos((d-1)/ex);
hold on
ang=(1:360)*pi/180;
fill(cos(ang),sin(ang),'c') %la Tierra
plot (cos(th_0),sin(th_0),'o','markersize',4,'markeredgecolor','r',
'markerfacecolor','r')
plot (0,0,'o','markersize',4,'markeredgecolor','b','markerfacecolor','b')
r=@(x) d./(1+ex*cos(x));
fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[0,2*pi],'lineStyle','--','color','b')
fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[th_0,2*pi-th_0])
fplot(@(x) cos(x),@(x)sin(x),[th_0,2*pi-th_0], 'lineWidth',1.5,'color','r')
hold off
axis equal
axis off

El punto de color rojo, es la posición de disparo, el arco de color rojo es el alcance. La trayectoria del proyectil es el arco de elipse cuyo foco está en el centro de la Tierra

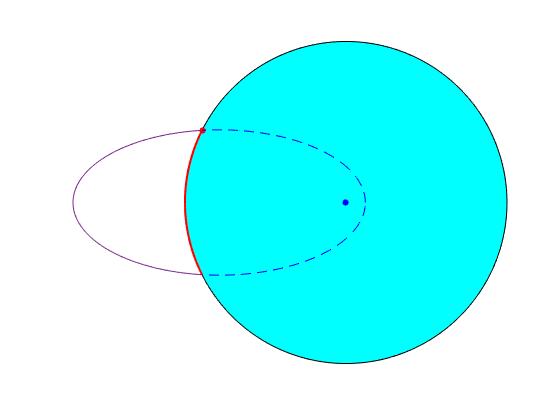
Alcance (km) es 5923.7
El tiempo de vuelo (min) es 53.7

Velocidad de disparo mínima

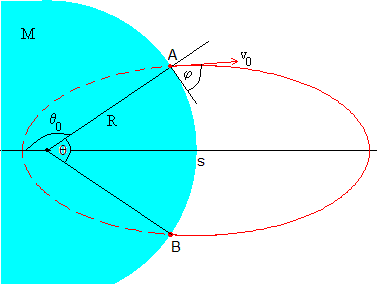
Dos localidades A y B distan un arco de longitud s=Rθ, o un ángulo θ. Vamos a encontrar la velocidad mínima de disparo v₀ de un proyectil en A para que impacte en B

Como apreciamos en la figura, θ=2(π-θ₀)

El proyectil sale de la posición R, θ₀, y llega a la posición R, -θ₀, donde

${\displaystyle \begin{array}{l}R=\frac{d}{1+\epsilon \cos {\theta }_0}\\ R=\frac{d}{1-\epsilon \cos \left(\frac{\theta }{2}\right)}\end{array}}$

Para simplificar las expresiones denominamos

${\displaystyle k=\frac{R{v}_0^2}{GM},k<2}$

Las expresiones del parámetro d, excentricidad ε, (véase el principio de la página) son

${\displaystyle \begin{array}{l}d=\frac{L^2}{GM{m}^2}=Rk{\cos }^2\phi \hfill \\ \epsilon =\sqrt{1+\frac{2L^{2}E}{G^2{M}^2{m}^3}}=\sqrt{1-k(2-k){\cos }^2\phi }=\sqrt{1-(2-k)\frac{d}{R}}\hfill \end{array}}$

Elevamos la excentricidad ε al cuadrado y despejamos k

${\displaystyle \begin{array}{l}{\epsilon }^2=1-(2-k)\left(1-\epsilon \cos \left(\frac{\theta }{2}\right)\right)\\ k=2-\frac{1-{\epsilon }^2}{1-\epsilon \cos \left(\frac{\theta }{2}\right)}\end{array}}$

Para que v₀ sea mínima o k sea mínima, derivamos respecto de la excentricidad ε e igualamos a cero

${\displaystyle \begin{array}{l}\frac{dk}{d\epsilon }=-\frac{-2\epsilon \left(1-\epsilon \cos \left(\frac{\theta }{2}\right)\right)+\cos \left(\frac{\theta }{2}\right)\left(1-{\epsilon }^2\right)}{{\left(1-\epsilon \cos \left(\frac{\theta }{2}\right)\right)}^2}=0\\ 2\epsilon \left(1-\epsilon \cos \left(\frac{\theta }{2}\right)\right)-\cos \left(\frac{\theta }{2}\right)\left(1-{\epsilon }^2\right)=0\\ {\epsilon }^2\cos \left(\frac{\theta }{2}\right)-2\epsilon +\cos \left(\frac{\theta }{2}\right)=0\\ \epsilon =\frac{1-\sin \left(\frac{\theta }{2}\right)}{\cos \left(\frac{\theta }{2}\right)}\end{array}}$

La otra solución, ε=(1+sin(θ/2))/cos(θ/2), implica que la excentricidad ε>1, la trayectoria, por tanto, no es elíptica

Sustituimos ε en la expresión de k

${\displaystyle \begin{array}{l}k=2-\frac{1-{\left(\frac{1-\sin \left(\frac{\theta }{2}\right)}{\cos \left(\frac{\theta }{2}\right)}\right)}^2}{\sin \left(\frac{\theta }{2}\right)}=\frac{2\sin \left(\frac{\theta }{2}\right){\cos }^2\left(\frac{\theta }{2}\right)-{\cos }^2\left(\frac{\theta }{2}\right)+1+{\sin }^2\left(\frac{\theta }{2}\right)-2\sin \left(\frac{\theta }{2}\right)}{{\cos }^2\left(\frac{\theta }{2}\right)\sin \left(\frac{\theta }{2}\right)}=\\ \frac{2{\cos }^2\left(\frac{\theta }{2}\right)+2\sin \left(\frac{\theta }{2}\right)-2}{{\cos }^2\left(\frac{\theta }{2}\right)}=\frac{2\sin \left(\frac{\theta }{2}\right)\left(1-\sin \left(\frac{\theta }{2}\right)\right)}{\left(1-\sin \left(\frac{\theta }{2}\right)\right)\left(1+\sin \left(\frac{\theta }{2}\right)\right)}=\frac{2\sin \left(\frac{\theta }{2}\right)}{1+\sin \left(\frac{\theta }{2}\right)}\end{array}}$

La velocidad de disparo mínima es

${\displaystyle \begin{array}{l}\frac{R{v}_0^2}{GM}=\frac{2\sin \left(\frac{\theta }{2}\right)}{1+\sin \left(\frac{\theta }{2}\right)}\\ v_0=\sqrt{\frac{GM}{R}\frac{2\sin \left(\frac{\theta }{2}\right)}{1+\sin \left(\frac{\theta }{2}\right)}}\end{array}}$

La distancia angular entre dos ciudades A y B es θ=120°, determinar la velocidad de disparo v₀ mínima en A para que impacte en B

R=6.37e6; %radio de la Tierra
M=5.97e24; %masa de la Tierra
G=6.67e-11; %constante G
th=115.05*pi/180; %distancia angular
v0=sqrt(2*G*M*sin(th/2)/(R*(1+sin(th/2))));
disp(v0)

La velocidad mínima es v₀=7 617 m/s

7.6173e+03

Ejemplo

En este ejemplo, calcularemos la velocidad mínima con la que hemos de disparar un proyectil desde el polo Norte para que llegue al Ecuador, la distancia angular es θ=π/2

Para el valor mínimo de la velocidad de disparo v₀, la excentricidad vale

${\displaystyle \epsilon =\sqrt{2}-1}$

Para este valor de ε,

${\displaystyle \begin{array}{l}k=2\sqrt{2}-\mathrm{2,}{v}_0^2=\left(\sqrt{2}-1\right)\frac{2GM}{R}=\left(\sqrt{2}-1\right)v_e^2\\ d=Rk{\cos }^2\phi ,\cos \phi =\frac{1}{2}\sqrt{\frac{\sqrt{2}}{\sqrt{2}-1}}\end{array}}$

La velocidad de disparo es v₀=7 202 m/s, el ángulo de tiro, φ=22.5°. El alcance es un cuarto de la circunferencia de la Tierra 2πR/4=10 006 km

R=6.37e6; %radio de la Tierra
M=5.98e24; %masa de la Tierra
G=6.67e-11; %constante G

k=2*sqrt(2)-2;
phi=acos(sqrt(sqrt(2)/(sqrt(2)-1))/2);
% v0=sqrt(k*G*M/R); %velocidad de disparo

%trayectoria
d=k*cos(phi)^2;
ex=sqrt(2)-1;
th_0=pi-pi/4;
alcance=2*R*acos((1-k*cos(phi)^2)/sqrt(1+k*(k-2)*cos(phi)^2)); %alcance
%tiempo de vuelo
alpha=asin(sqrt(k*(2-k))*sin(phi)/sqrt(1-k*(2-k)*cos(phi)^2));
if k<=1
    T=2*(alpha+sqrt(k*(2-k))*sin(phi))*sqrt((R/(2-k))^3)/sqrt(G*M);
else
     T=2*(pi-alpha+sqrt(k*(2-k))*sin(phi))*sqrt((R/(2-k))^3)/sqrt(G*M);
end 
fprintf('Alcance (km) es %2.1f\n',alcance/1000)
fprintf('El tiempo de vuelo (min) es %4.1f\n',T/60)

hold on
ang=(1:360)*pi/180;
fill(cos(ang),sin(ang),'c') %la Tierra
plot (-1,0,'o','markersize',4,'markeredgecolor','r','markerfacecolor','r')
plot (0,1,'o','markersize',4,'markeredgecolor','r','markerfacecolor','r')
plot (0,0,'o','markersize',4,'markeredgecolor','b','markerfacecolor','b')
r=@(x) d./(1+ex*cos(x+pi/4));
fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[0,2*pi],
'lineStyle','--','color','b')
fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[th_0-pi/4,2*pi-th_0-pi/4])
hold off
axis equal
axis off

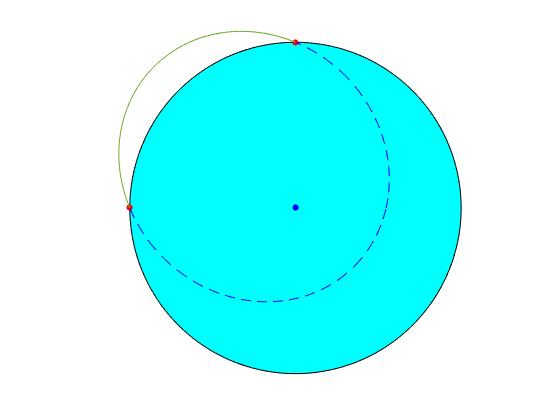
Alcance (km) es 10006.0
El tiempo de vuelo (min) es 32.2

Hemos girado la elipse π/4, para que la posición de disparo coincida con el polo Norte y la de impacto con el Ecuador

Actividades

Se introduce

• La velocidad de disparo v₀ menor que la velocidad de escape v_e=11191 m/s, en el control titulado Velocidad.
• El ángulo de tiro φ, con la horizontal local, en el control titulado Ángulo.

Se pulsa el botón titulado Nuevo

Se observa la trayectoria seguida por el proyectil. En la parte superior derecha, se proporcionan los datos de la distancia al centro de la Tierra medido en radios terrestres, el tiempo en segundos y el alcance del proyectil (medida del arco entre el punto de lanzamiento y de impacto, en km)

Se tiene en cuenta la rotación de la Tierra

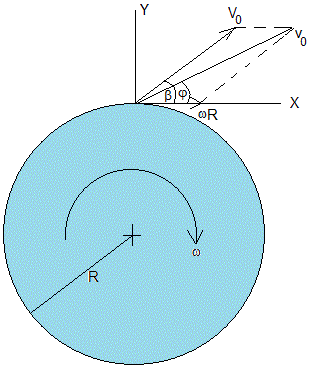
La Tierra gira alrededor de su eje, con velocidad angular constante ω=2π/(24·60·60)=7.27·10^-5 rad/s. La velocidad de un punto situado en el ecuador es ωR=463.24 m/s, siendo R el radio de la Tierra. Supongamos que lanzamos un proyectil desde la superficie de la Tierra, en el ecuador, con velocidad V₀ haciendo un ángulo β con la horizontal local. La velocidad v₀ del proyectil y el ángulo de tiro φ para el observador inercial son:

${\displaystyle \begin{array}{l}\{\begin{array}{l}{v}_0\sin \phi =V_0\sin \beta \\ v_0\cos \phi =V_0\cos \beta +\omega R\end{array}\\ \{\begin{array}{l}{v}_0^2=V_0^2+{\omega }^2{R}^2+2V_0\omega R\cos \beta \\ \tan \phi =\frac{V_0\sin \beta }{V_0\cos \beta +\omega R}\end{array}\end{array}}$

Mientras el proyectil describe la trayectoria, la Tierra gira, la posición de disparo se desplaza un arco ωt·R. El alcance medido desde la posición de disparo es s-ωT·R, donde s es el alcance calculado para un proyectil que se dispara con velocidad v₀, haciendo un ángulo φ, con la horizontal local, suponiendo que la Tierra no gira y T es el tiempo de vuelo del proyectil.

Disparamos un proyectil desde algún lugar del ecuador con velocidad inicial v₀= 7500 m/s en la dirección que hace φ=60º con el plano local.

R=6.37e6; %radio de la Tierra
M=5.98e24; %masa de la Tierra
G=6.67e-11; %constante G
w=2*pi/(24*60*60); %velocidad angular de la Tierra

V0=7500; %velocidad de disparo, en el plano local
beta=60*pi/180; %ángulo de tiro

%sistema de referencia inercial
v0=sqrt(V0^2+(w*R)^2+2*V0*w*R*cos(beta));
phi=atan2(V0*sin(beta),V0*cos(beta)+w*R);
k=R*v0^2/(G*M);
alcance=2*R*acos((1-k*cos(phi)^2)/sqrt(1+k*(k-2)*cos(phi)^2)); 
%tiempo de vuelo
alpha=asin(sqrt(k*(2-k))*sin(phi)/sqrt(1-k*(2-k)*cos(phi)^2));
if k<=1
    T=2*(alpha+sqrt(k*(2-k))*sin(phi))*sqrt((R/(2-k))^3)/sqrt(G*M);
else
     T=2*(pi-alpha+sqrt(k*(2-k))*sin(phi))*sqrt((R/(2-k))^3)/sqrt(G*M);
end 
fprintf('Alcance (km) es %2.1f\n',(alcance-w*T*R)/1000)
fprintf('El tiempo de vuelo (min) es %4.1f\n',T/60)

%trayectoria
d=k*cos(phi)^2;
ex=sqrt(1-k*(2-k)*cos(phi)^2);
th_0=acos((d-1)/ex);
hold on
ang=(1:360)*pi/180;
fill(cos(ang),sin(ang),'c') %la Tierra
plot (cos(th_0),sin(th_0),'o','markersize',4,'markeredgecolor','r',
'markerfacecolor','r')
plot (cos(th_0+w*T),sin(th_0+w*T),'o','markersize',4,'markeredgecolor',
'b','markerfacecolor','b')
plot (0,0,'o','markersize',4,'markeredgecolor','b','markerfacecolor','b')
r=@(x) d./(1+ex*cos(x));
fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[0,2*pi],'lineStyle','--')
fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[th_0,2*pi-th_0])
fplot(@(x) cos(x),@(x)sin(x),[th_0+w*T,2*pi-th_0], 'lineWidth',1.5,'color','r')
hold off
axis equal
axis off

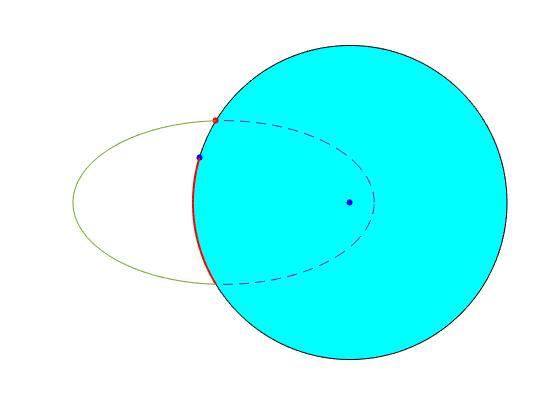
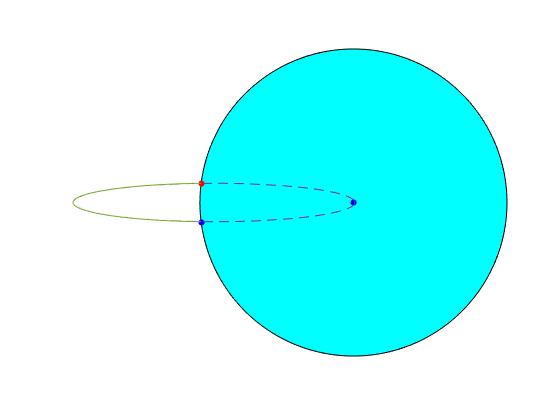
El punto de color rojo es la posición de disparo en el instante t=0. El punto de color azul es la posición de disparo en el instante T cuando el proyectil impacta en la superficie de la Tierra. El alcance es el arco de color rojo, la distancia entre la posición de disparo y la de impacto

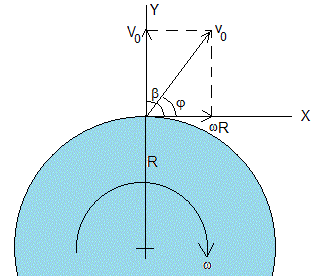
Cuando el ángulo de tiro es β=90°, el momento angular vale L=m·R·ωR=mωR². La constancia del momento angular implica que

${\displaystyle m{r}^2\frac{d\theta }{dt}=m{R}^2\omega \frac{d\theta }{dt}=\frac{R^2}{r^2}\omega }$

dado que la distancia entre el proyectil y el centro de la Tierra, r, es mayor que el radio de la Tierra, r>R, entonces, dθ/dt<ω. El punto de impacto se encontrará por detrás de la posición de disparo

En el script hacemos el ángulo de tiro β=90°. En la figura que obtenemos, observamos la posición inicial de disparo, el punto de color rojo, la posición de disparo al cabo de un tiempo T (tiempo de vuelo), el punto de color azul que está por detrás de la posición de impacto

...
beta=90*pi/180; %ángulo de tiro
...

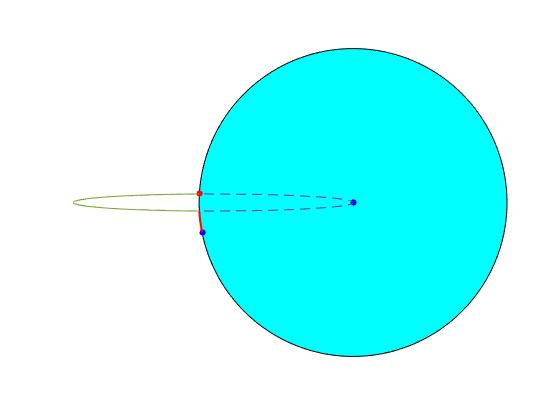
Podríamos pensar que hay un ángulo de tiro β<90° para el cual coinciden la posición de disparo con la de impacto. Para ello, tenemos que resolver la ecuación trascendente s-ωT·R con el ángulo φ como incógnita a partir del cual, calculamos el ángulo de disparo β

${\displaystyle \begin{array}{l}s-\omega RT=0\\ \arccos \frac{1-k{\cos }^2\phi }{\sqrt{1+k\left(k-2\right){\cos }^2\phi }}-\\ \omega \sqrt{\frac{R^3}{GM}}\left(\arcsin \left(\frac{\sqrt{k(2-k)}\sin \phi }{\sqrt{1-k\left(2-k\right){\cos }^2\phi }}\right)+\sqrt{k(2-k)}\sin \phi \right)\sqrt{\frac{1}{{(2-k)}^3}}=0\end{array}}$

En el supuesto que el parámetro k<1

>> f=@(phi) acos((1-k*cos(phi)^2)/sqrt(1+k*(k-2)*cos(phi)^2))-
w*(asin(sqrt(k*(2-k))*sin(phi)/sqrt(1-k*(2-k)*cos(phi)^2))+
sqrt(k*(2-k))*sin(phi))*sqrt((R/(2-k))^3)/sqrt(G*M);
>> ang=fzero(f,pi/2);
>> atan(v0*sin(ang)/(v0*cos(ang)-w*R))*180/pi
ans =   85.5776
>> k
k =    0.9018

Cambiamos el ángulo de tiro a β=85.6°, comprobando que coinciden la posición de disparo con la de impacto,

...
beta=85.6*pi/180; %ángulo de tiro
...

Referencias

Francisco G. M. Orlando, C. Farina, Carlos A. D. Zarro. Kepler's equation and some of its pearls. Am. J. Phys. 86 (11) November 2018, pp. 849-858

Physics Challenge for Teachers and Students. One Giant Leap. The Physics Teacher Vol. 50, December 2012, pp. 568

2021 Online Physics Olympiad: Open Contest. pp. 26-27. Problem 25