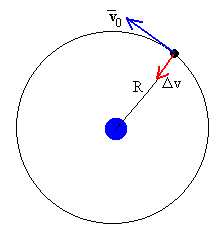
Consideremos un satélite de comunicación de masa m situado en la órbita geoestacionaria. Debido a un error de los controladores en Tierra, que accionan los motores que proporcionan un empuje al satélite en la dirección radial  dirigido hacia la Tierra. Como consecuencia una variación no deseada de la velocidad Δv se proporciona al satélite, tal como se muestra en la figura.

Caracterizamos dicho impulso por el parámetro β= Δv/v₀. Donde v₀ es la velocidad del satélite en su órbita circular. Se supondrá que los motores están encendidos durante un intervalo de tiempo muy pequeño comparado con el periodo de la órbita, se considera un impulso instantáneo.

Órbita circular

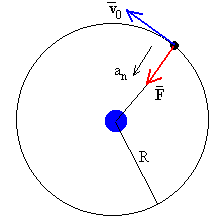
Si R es el radio de la órbita circular del satélite, aplicando la dinámica del movimiento circular uniforme: la masa del cuerpo m por la aceleración normal es igual a la fuerza F de atracción que ejerce la Tierra sobre el satélite.

${\displaystyle m\frac{v_0^2}{R}=G\frac{Mm}{R^2}{v}_0^2=\frac{GM}{R}}$

La energía del satélite en la órbita circular es

${\displaystyle E_0=\frac{1}{2}m{v}_0^2-G\frac{Mm}{R}=-\frac{1}{2}\frac{GMm}{R}=-\frac{1}{2}m{v}_0^2}$

El momento angular del satélite es

L=mRv₀

Trayectoria elíptica

Si se proporciona al satélite una velocidad Δv en la dirección radial.

El momento angular del satélite es el mismo que el que tenía en la órbita circular,  ya que la variación de velocidad Δv tiene dirección radial.

L=mRv₀

La energía del satélite es

$$\begin{gathered} {\displaystyle E=\frac{1}{2}m\left(v_0^2+\Delta v^2\right)-G\frac{Mm}{R}=E_0+\frac{1}{2}m\Delta v^2=-\frac{1}{2}m{v}_0^2+\frac{1}{2}m\Delta v^2= \\ \frac{1}{2}m{v}_0^2\left({\beta }^2-1\right)} \end{gathered}$$

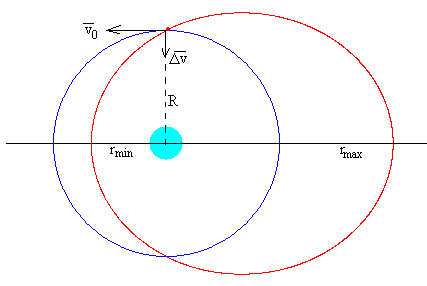
Si β<1 la energía total E<0, el satélite describe una órbita elíptica. La ecuación de la trayectoria  es

${\displaystyle r=\frac{d}{1+\epsilon \cos (\theta )}}$

La excentricidad ε y el parámetro d valen, respectivamente

${\displaystyle \begin{array}{l}\epsilon =\sqrt{1+\frac{2L^{2}E}{m^3{G}^2{M}^2}}=\sqrt{1+\frac{R^2{v}_0^4({\beta }^2-1)}{G^2{M}^2}}=\beta \\ d=\frac{L^2}{GM{m}^2}=\frac{R^2{v}_0^2}{GM}=R\end{array}}$

El valor máximo y mínimo de r se obtiene para θ=π y θ=0, respectivamente.

${\displaystyle r_{max}=\frac{R}{1-\beta }{r}_{\min }=\frac{R}{1+\beta }}$

Estas distancias se pueden también obtener a partir de la conservación del momento angular y de la energía

${\displaystyle \begin{array}{l}mvr=mR{v}_0\\ \frac{1}{2}m{v}^2-G\frac{Mm}{r}=\frac{1}{2}m{v}_0^2\left({\beta }^2-1\right)\end{array}}$

Despejamos r en la primera ecuación y la sustituimos en la segunda. La ecuación de segundo grado en v tiene dos soluciones

${\displaystyle \begin{array}{l}{v}^2-2v_{0}v-v_0^2({\beta }^2-1)=0\\ v_{\min }=v_0(1-\beta )v_{\max }=v_0(1+\beta )\\ r_{\max }=\frac{R}{1-\beta }{r}_{\min }=\frac{R}{1+\beta }\end{array}}$

El semieje mayor de la elipse es

${\displaystyle a=\frac{r_{\min }+r_{\max }}{2}=\frac{R}{1-{\beta }^2}}$

El periodo

${\displaystyle P^2=\frac{4{\pi }^2{a}^3}{\left(GM\right)}=\frac{4{\pi }^2{R}^3}{GM{(1-{\beta }^2)}^3}=\frac{4{\pi }^2{R}^2}{v_0^2{(1-{\beta }^2)}^3}=\frac{P_0^2}{{(1-{\beta }^2)}^3}}$

Ejemplo

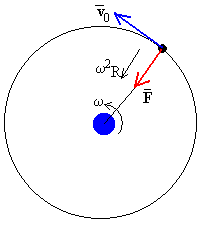
La Tierra tarda en dar una vuelta alrededor de su eje en 24 h, su velocidad angular de rotación es

${\displaystyle \omega =\frac{2\pi }{24·60·60}=7.272·{10}^{-5}\text{rad/s}}$

Un satélite artificial que describe una órbita circular con el mismo periodo que la rotación de la Tierra se denomina geoestacionario. Un observador situado en la línea que une el centro de la Tierra y el satélite lo vería inmóvil en la misma posición.

Si R es el radio de la órbita circular del satélite, aplicando la dinámica del movimiento circular uniforme, la masa del cuerpo m por la aceleración normal ω²R es igual a la fuerza F de atracción que ejerce la Tierra sobre el satélite.

${\displaystyle \begin{array}{l}m{\omega }^{2}R=G\frac{Mm}{r^2}{R}^3=\frac{GM}{{\omega }^2}\\ R^3=\frac{6.67·{10}^{-11}·5.98·{10}^{24}}{{\left(\frac{2\pi }{24·60·60}\right)}^2}R=42250\text{km}\end{array}}$

Sea β=0.5

La trayectoria es una elipse. El apogeo y el perigeo se encuentra a una distancia del centro de la Tierra de

${\displaystyle \begin{array}{l}{r}_{\max }=\frac{R}{1-\beta }=\frac{42250}{1-0.5}=84500\text{km}\\ r_{\min }=\frac{R}{1+\beta }=\frac{42250}{1+0.5}=28167\text{km}\end{array}}$

El periodo P de la órbita es

${\displaystyle P^2=\frac{P_0^2}{{(1-{\beta }^2)}^3}P=\frac{24}{{\left(1-{0.5}^2\right)}^{3/2}}=37\text{h}}$

Trayectoria hiperbólica

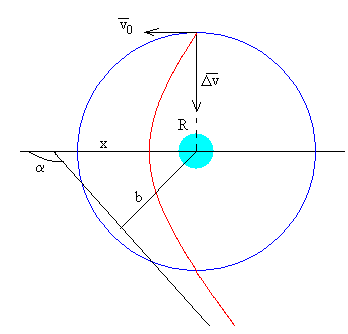
Para que el satélite escape de la atracción de la Tierra su energía E≥0, es decir, la excentricidad ε o β tiene que ser mayor o igual a 1, la trayectoria es una hipérbola.

La velocidad del satélite cuando está lejos de la Tierra es

${\displaystyle \begin{array}{l}E=\frac{1}{2}m{v}_{\infty }^2=\frac{1}{2}m{v}_0^2\left({\beta }^2-1\right)\\ v_{\infty }=v_0\sqrt{{\beta }^2-1}\end{array}}$

El movimiento es rectilíneo y uniforme. La dirección de la velocidad es la asíntota de la hipérbola. La asíntota está a una distancia b del centro de la Tierra. El momento angular L es

${\displaystyle \begin{array}{l}L=m{v}_{0}R=m{v}_{\infty }b\\ b=\frac{R}{\sqrt{{\beta }^2-1}}\end{array}}$

De la ecuación de la trayectoria obtenemos el ángulo para el cual r→∞,

${\displaystyle \alpha =\arccos \left(-\frac{1}{\epsilon }\right)=\arccos \left(-\frac{1}{\beta }\right)}$

La asíntota corta al eje horizontal a una distancia x del centro de fuerzas.

${\displaystyle x=\frac{b\epsilon }{\sqrt{{\epsilon }^2-1}}=\frac{R\beta }{{\beta }^2-1}}$

Ejemplo

Sea β=1.5

La trayectoria es una hipérbola. El satélite se acerca hacia la Tierra hasta una distancia

${\displaystyle r_{\min }=\frac{R}{1+\beta }=\frac{42250}{1+1.5}=16900\text{km}}$

La asíntota forma un ángulo de α con el eje X

${\displaystyle \alpha =\arccos \left(-\frac{1}{\beta }\right)=132º}$

corta al eje X a la distancia

${\displaystyle x=\frac{R\beta }{{\beta }^2-1}=\frac{42250·1.5}{{1.5}^2-1}=50700\text{km}}$

Actividades

Se introduce

• El parámetro β=Δv/v₀ en el control titulado beta

Se pulsa el botón titulado Nuevo

Observamos la nave espacial describiendo la órbita circular geoestacionaria. Una flecha de color azul muestra la velocidad de la nave v₀, cuya dirección es tangente a la circunferencia.

Se pulsa el botón titulado Lanza

Se pulsa el botón titulado || para detener el movimiento de la nave, cuando completa la trayectoria elíptica o cuando sale de los límites de de la ventana.

Se observa por un momento una flecha de color rojo que muestra el impulso radial y dirigido hacia la Tierra que los motores proporcionan a la nave y que cambia la velocidad de la nave Δv en la dirección radial.

Referencias

An ill fated satellite. 36^th International Physics Olympiad. Salamanca. Spain ( 2005)