En vez de disparar en la dirección radial, disparamos en la dirección transversal, tangente a la superficie de la Tierra, de modo que el proyectil sigue una trayectoria elíptica hasta que impacta con el satélite.

Trayectoria del proyectil

Calculamos la energía total y el momento angular en la posición inicial del proyectil

${\displaystyle \begin{array}{l}L=mR{v}_0\\ E=\frac{1}{2}m{v}_0^2-\frac{GMm}{R}\end{array}}$

La ecuación de la trayectoria es

${\displaystyle r=\frac{d}{1+\epsilon \cos \theta }\epsilon =\sqrt{1+\frac{2L^{2}E}{m^3{G}^2{M}^2}}d=\frac{L^2}{GM{m}^2}}$

El apogeo del proyectil se obtiene cuando θ=π.

${\displaystyle r_P=\frac{d}{1-\epsilon }{r}_P=\frac{R^2{v}_0^2}{GM-\sqrt{G^2{M}^2-R{v}_0^2\left(2GM-v_0^{2}R\right)}}}$

Este resultado se puede obtener aplicando la constancia del momento angular y la energía en todos los puntos de la trayectoria y en particular, en el apogeo r_p y en el perigeo R

${\displaystyle \{\begin{array}{l}{v}_{0}R=v_p{r}_p\\ \frac{1}{2}{v}_0^2-\frac{GM}{R}=\frac{1}{2}{v}_p^2-\frac{GM}{r_p}\end{array}}$

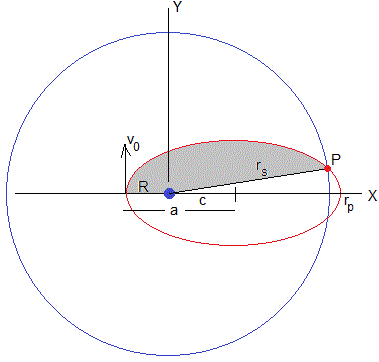
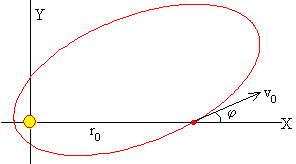
Supongamos que la trayectoria elíptica del proyectil alcanza la órbita circular del satélite, es decir r_p>r_s, tal como se muestra en la figura. Calculamos las coordenadas del punto de intersección P

Situamos el origen en el centro de la Tierra y los ejes X e Y tal como se muestra en la figura. Escribimos la ecuación de la circunferencia con centro en el origen y radio r_s y la ecuación de la elipse centrada en el punto (c,0), de semiejes a y b.

${\displaystyle \begin{array}{l}{x}^2+y^2=r_s^2\\ \frac{{\left(x-c\right)}^2}{a^2}+\frac{y^2}{b^2}=1\end{array}}$

Relacionamos los semiejes a, b y la semidistancia focal c

${\displaystyle \begin{array}{l}2a=R+r_p=\frac{d}{1+\epsilon }+\frac{d}{1-\epsilon }=\frac{2d}{1-{\epsilon }^2}\\ c=\epsilon a\\ b=\sqrt{a^2-c^2}\end{array}}$

La abscisa del punto de intersección P es

${\displaystyle x_p=\frac{a{r}_s-b^2}{c}}$

El ángulo del punto de impacto P es

${\displaystyle {\theta }_p=\pi -\arccos \left(\frac{x_p}{r_s}\right)}$

Duración del vuelo del proyectil

Calculamos el tiempo que tarda el proyectil en alcanzar la órbita del satélite

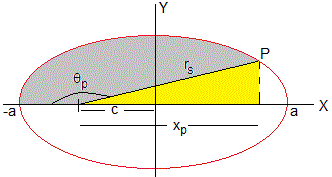
El momento angular se expresa en coordenadas polares

${\displaystyle L=m{r}^2\frac{d\theta }{dt}}$

Calculamos el área barrida por el radio vector, entre el instante t=0 y el instante t_p, cuando el ángulo θ varía de 0 a θ_p. Siendo θ_p la posición angular el punto P

${\displaystyle {\displaystyle \underset{0}{\overset{{\theta }_p}{\int }}\frac{1}{2}{r}^{2}d\theta =\frac{L}{2m}}{\displaystyle \underset{0}{\overset{t_p}{\int }}dt}}$

El primer miembro es el área sombreada de color gris en la figura, que es la diferencia entre dos áreas: el área de la porción de elipse comprendida entre -a y x_p-c y el área del triángulo sombreado de color amarillo

${\displaystyle {\displaystyle \underset{-a}{\overset{x_p-c}{\int }}b\sqrt{1-\frac{x^2}{a^2}}}dx-\left(\frac{x_p\sqrt{r_s^2-x_p^2}}{2}\right)}$

Para calcular la primera integral, hacemos el cambio de variable x=a·sin(z)

${\displaystyle \begin{array}{l}{\displaystyle \underset{z_1}{\overset{z_2}{\int }}ab}{\cos }^{2}z·dz-\left(\frac{x_p\sqrt{r_s^2-x_p^2}}{2}\right)=\\ \frac{ab}{2}\left(z_2+\frac{1}{2}\sin \left(2z_2\right)+\frac{\pi }{2}\right)-\frac{x_p\sqrt{r_s^2-x_p^2}}{2}\end{array}}$

con z₁=-π/2 y x_p-c=a·sin(z₂)

Una vez calculada el área barrida por el radio vector, calculamos el tiempo t_p que tarda el proyectil desde que es lanzado en la superficie de la Tierra hasta que se encuentra con el satélite

${\displaystyle t_P=\frac{1}{R{v}_0}\left(ab\left(z_2+\frac{1}{2}\sin \left(2z_2\right)+\frac{\pi }{2}\right)-x_p\sqrt{r_s^2-x_p^2}\right)}$

Disparamos un proyectil de masa m desde la superficie de la tierra con una velocidad v₀=0.95·v_e en dirección tangente a la superficie. Comprobamos que el proyectil alcanza la órbita circular del satélite de radio r_s=5·R. Calculamos el punto de intersección y el tiempo que tarda el proyectil en alcanzarlo

GM=6.67e-11*5.98e24;
R=6.37e6; %radio de la Tierra
rS=5*R; 
vS=sqrt(GM/rS);
ve=sqrt(2*GM/R); %velocidad de escape
v0=0.95*ve; %velocidad de disparo del proyectil
d=(R*v0)^2/GM;
epsilon=sqrt(1-R*v0^2*(2*GM-R*v0^2)/GM^2);
hold on
%la Tierra
th=(0:360)*pi/180;
fill(cos(th),sin(th),'b')
fplot(@(x) rS*cos(x)/R, @(x) rS*sin(x)/R,[0,2*pi])
%tiempo 
rP=(R*v0)^2/(GM-sqrt(GM^2-R*v0^2*(2*GM-v0^2*R)));
r=@(x) d./(1+epsilon*cos(x));
if rP>rS
    a=(R+rP)/2;
    c=epsilon*a;
    b=sqrt(a^2-c^2);
    xP=(a*rS-b^2)/c; %abscisa del punto de intersección
    z2=asin(xP-c)/a;
    tP=(a*b*(z2+sin(2*z2)/2+pi/2)-xP*sqrt(rS^2-xP^2))/(R*v0);
    fprintf('En %3.1f min, el proyectil choca con el satélite\n',tP/60)
    fplot(@(x) r(x).*cos(x)/R, @(x) r(x).*sin(x)/R,[0,2*pi],'lineStyle','--') 
    th=pi-acos(xP/rS); %posición de impacto P
    fplot(@(x) r(x).*cos(x)/R, @(x) r(x).*sin(x)/R,[0,th]) 
    plot(r(th)*cos(th)/R,r(th)*sin(th)/R,'ro', 'markersize',4,
'markerfacecolor','r')
  else
     fplot(@(x) r(x).*cos(x)/R, @(x) r(x).*sin(x)/R,[0,2*pi]) 
end
hold off
axis equal
grid on
xlabel('x')
ylabel('y')
title('Intersección de las órbitas')

En 124.2 min, el proyectil choca con el satélite

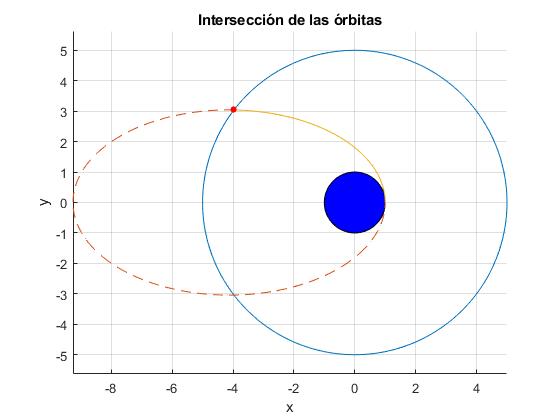
Choque del proyectil con el satélite

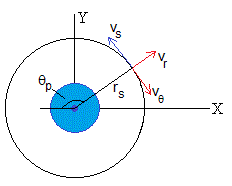
En la posición de impacto, θ_p el proyectil dista r_s del centro de la Tierra. La velocidad del proyectil tiene dos componentes, una radial v_r y otra transversal v_θ. La primera se calcula a partir de la energía y la segunda a partir del momento angular

${\displaystyle \begin{array}{l}E=\frac{1}{2}m{\left(\frac{dr}{dt}\right)}^2+\frac{L^2}{2m{r}^2}-\frac{GMm}{r}{v}_r=\frac{dr}{dt}\\ L=m{r}^2\left(\frac{d\theta }{dt}\right)v_{\theta }=r\frac{d\theta }{dt}\end{array}}$

Donde E y L son la energía y momento angular calculados en la posición inicial

Aplicamos el principio de conservación del momento lineal, para calcular la velocidad del objeto resultado del choque inelástico

${\displaystyle m{v}_r\widehat{i}+m\left(v_s-v_{\theta }\right)\widehat{j}=2m\overrightarrow{v}}$

Las componentes de la velocidad después del choque son

${\displaystyle v_x=\frac{v_r}{2},v_y=\frac{v_s-v_{\theta }}{2}}$

Trayectoria del objeto formado por el satélite y el proyectil

Para representar la trayectoria de un elipse girada es más conveniente utilizar esta ecuación

${\displaystyle \begin{array}{l}\frac{r_0}{r}=-\frac{\cos \phi }{\sin \phi }\sin \theta +\cos \theta +\frac{p(1-\cos \theta )}{2{\sin }^2\phi }\\ p=\frac{2GM}{r_0{v}_0^2}\end{array}}$

p es un parámetro adimensional

La posición inicial del objeto después del choque no es θ=0 como en la figura, sino θ=θ_p

Disparamos un proyectil de masa m desde la superficie de la Tierra con una velocidad v₀=0.95·v_e en dirección tangente a la superficie. Representamos la trayectoria del proyectil, del satélite y del objeto resultado del choque inelástico entre el proyectil y el satélite

GM=6.67e-11*5.98e24;
R=6.37e6; %radio de la Tierra
rS=10*R; 
vS=sqrt(GM/rS);
ve=sqrt(2*GM/R); %velocidad de escape
v0=0.96*ve; %velocidad de disparo del proyectil
d=(R*v0)^2/GM;
epsilon=sqrt(1-R*v0^2*(2*GM-R*v0^2)/GM^2);
hold on
%la Tierra
th=(0:360)*pi/180;
fill(cos(th),sin(th),'b')
fplot(@(x) rS*cos(x)/R, @(x) rS*sin(x)/R,[0,2*pi])
%tiempo 
rP=(R*v0)^2/(GM-sqrt(GM^2-R*v0^2*(2*GM-v0^2*R)));
r=@(x) d./(1+epsilon*cos(x));
a=(R+rP)/2;
c=epsilon*a;
b=sqrt(a^2-c^2);
xP=(a*rS-b^2)/c; %abscisa del punto de intersección
z2=asin(xP-c)/a;
tP=(a*b*(z2+sin(2*z2)/2+pi/2)-xP*sqrt(rS^2-xP^2))/(R*v0);
fprintf('El tiempo %3.1f min, de choque con el satélite\n',tP/60)
th=pi-acos(xP/rS); %intersección
fplot(@(x) r(x).*cos(x)/R, @(x) r(x).*sin(x)/R,[0,th]) 
plot(r(th)*cos(th)/R,r(th)*sin(th)/R,'ro', 'markersize',4,
'markerfacecolor','r')

%choque
mAngular=R*v0;
energia=v0^2/2-GM/R;
%componentes de la velocidad después del choque en el punto de impacto rS
vX=sqrt(2*energia-mAngular^2/rS^2+2*GM/rS)/2; %componente radial 
vY=(-mAngular/rS+vS)/2; %componente transversal 
v0=sqrt(vX^2+vY^2);
phi=atan2(vY,vX);
p=2*GM/(rS*v0^2);
r=@(x) (rS/R)./(-cos(phi)*sin(x-th)/sin(phi)+cos(x-th)+
p*(1-cos(x-th))/(2*sin(phi)^2));
fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[0,2*pi]) 
hold off
axis equal
grid on
xlabel('x')
ylabel('y')
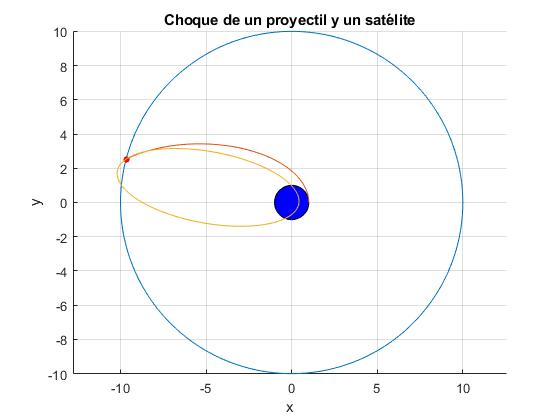
title('Choque de un proyectil y un satélite')

El tiempo 97.2 min, de choque con el satélite

En color azul, la órbita circular del satélite. En color rojo, la trayectoria elíptica del proyectil hasta que choca con el satélite. En amarillo, la trayectoria del objeto resultado de la colisión inelástica entre el proyectil y el satélite

Caso particular

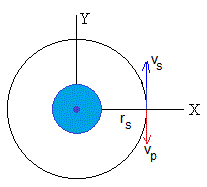
La situación más importante se produce cuando el apogeo del proyectil coincide con el radio de la órbita del satélite r_p=r_s, el resultado es una colisión frontal entre los dos objetos

Calculamos la velocidad v₀ con el que tendríamos que lanzar el proyectil para que su apogeo sea r_s. Aplicamos las propiedades de la fuerza de atracción: central y conservativa

${\displaystyle \begin{array}{l}R{v}_0=v_p{r}_s\\ \frac{1}{2}{v}_0^2-\frac{GM}{R}=\frac{1}{2}{v}_p^2-\frac{GM}{r_s}\end{array}}$

Despejamos v₀ y r_p

${\displaystyle v_0=\sqrt{\left(\frac{2GM}{r_s+R}\right)\frac{r_s}{R}}{v}_p=\sqrt{\left(\frac{2GM}{r_s+R}\right)\frac{R}{r_s}}}$

Aplicamos el principio de conservación del momento lineal, para calcular la velocidad del objeto de masa 2m después del choque inelástico

${\displaystyle \begin{array}{l}2mv=m{v}_s-m{v}_p\\ v=\frac{v_s-v_p}{2}=\frac{v_s}{2}\left(1-\sqrt{\frac{2R}{r_s+R}}\right)=\frac{v_s}{2}\delta \end{array}}$

Calculamos la energía y el momento angular en la situación inicial, justamente después del choque

${\displaystyle \begin{array}{l}E=\frac{1}{2}\left(2m\right)\frac{v_s^2}{4}{\delta }^2-\frac{GM\left(2m\right)}{r_s}\\ L=\left(2m\right)r_s\frac{v_s}{2}\delta \end{array}}$

Calculamos el parámetro d y la excentricidad ε

${\displaystyle d=\frac{r_s}{4}{\delta }^2\epsilon =1-\frac{{\delta }^2}{4}}$

La ecuación de la trayectoria es

${\displaystyle r=\frac{d}{1+\epsilon \cos \theta }}$

La distancia del centro de la Tierra al perigeo se obtiene con θ=0

${\displaystyle r_{\min }=\frac{r_s{\delta }^2}{4-{\delta }^2}}$

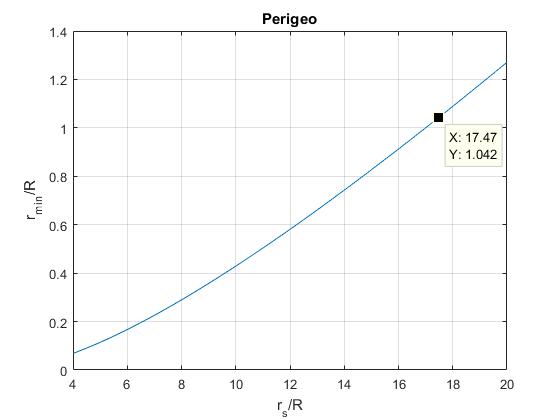
Representamos r_min/R en función de r_s/R. Vemos que r_min<R hasta r_s=17R, aproximadamente

delta=@(y) 1-sqrt(2/(y+1));
f=@(x) (x*delta(x)^2)/(8-delta(x)^2); 
fplot(f,[4,20])
grid on
xlabel('r_s/R')
ylabel('r_m_i_n/R')
title('Perigeo')
ff=@(x) f(x)-1;
fzero(ff,[15,18])

Con la función fzero de MATLAB obtenemos la raíz de la ecuación trascendente

ans =   17.0000

Actividades

Se introduce

• El radio de la órbita circular del satélite en unidades del radio de la Tierra R, en el control titulado Radio órbita
• La velocidad de disparo del proyectil desde la superficie de la Tierra, v₀, en unidades de la velocidad de escape v_e, en el control titulado Velocidad disparo

Se pulsa el botón titulado Nuevo

Observamos el movimiento del satélite en órbita circular de radio r_s y el proyectil disparado desde la superficie de la Tierra con velocidad v₀.

Puede ocurrir que la velocidad de disparo no sea suficiente para que el proyectil llegue a la órbita del satélite. El proyectil regresa a la superficie de la Tierra

Si la velocidad de disparo es suficiente. El proyectil choca con el satélite y se observa la trayectoria del objeto resultante. Si el perigeo es menor que el radio de la Tierra, el objeto se detiene cuando impacta en su superficie, el satélite ha sido derribado por el proyectil

Para que el proyectil llegue justamente a la órbita del satélite y choque frontalmente con éste, es preciso calcular la velocidad de disparo v₀ aplicando la conservación de la energía y después, introducirla en el control titulado Velocidad disparo en unidades de la velocidad de escape

${\displaystyle \frac{v_0}{v_e}=\sqrt{\frac{r_s/R}{1+r_s/R}}}$

Por ejempo, para r_s/R=10, v₀/v_e=0.9535

Referencias

Philip R Blanco, Carl E Mungan. Satellite splat II: an inelastic collision with a surface-launched projectile and the maximum orbital radius for planetary impact. Eur. J. Phys. 37 (2016) 045004.

Este artículo está disponible en la dirección: https://www.usna.edu/Users/physics/mungan/_files/documents/Publications/EJP19.pdf