Desviación hacia el este y hacia el sur de un cuerpo que cae
Supongamos que hemos construido sobre la superficie de la Tierra, supuesta esférica de radio R, un torre muy alta a lo largo de la dirección radial. La torre de altura h está situada en el hemisferio norte a una latitud λ. Dejamos caer una partícula de masa m y medimos la desviación hacia el este y hacia la sur del punto de impacto de la partícula respecto de la base de la torre.
Mientras la partícula llega a la superficie de la Tierra (en color rojo), la base de la torre (en color azul) se ha desplazado a lo largo del paralelo, debido a la rotación de la Tierra.
Sabiendo que la Tierra gira alrededor de su eje Z con velocidad angular constante de ω=2π/(24·60·60)=7.272·10-5 rad/s, dada la altura h de la torre, se trata de calcular las desviaciones e, hacia el este y s, hacia el Sur medidas desde la base de la torre, de una partícula que se deja caer desde lo alto de la torre.
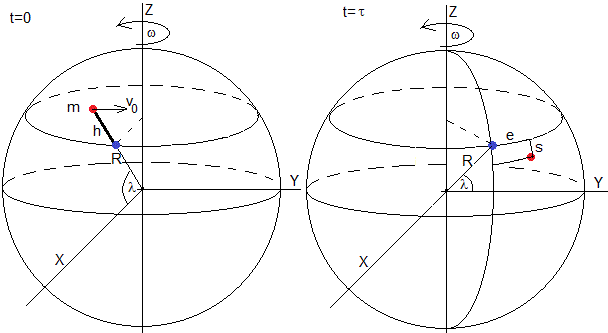
Situamos el Sistema de Referencia Inercial tal como se muestra en la figura, el eje Z es el eje de rotación de la Tierra. La torre y la partícula se encuentran en el instante t=0 en el plano XZ.
Trayectoria de la partícula
Como la partícula, situada inicialmente en el alto de la torre, t=0, describe una circunferencia de radio (R+h)cosλ, con velocidad angular ω. La velocidad inicial de la partícula es ω(R+h)cosλ, dirigida a lo largo del eje Y.
El momento angular respecto del origen es L=mω(R+h)2cosλ. La dirección del vector es perpendicular al plano formado por la dirección radial y la dirección de la velocidad inicial. La trayectoria de la partícula está contenida en este plano, que forma un ángulo λ con el plano XY (plano ecuatorial)
La energía de la partícula es
La partícula describe una trayectoria elíptica cuyo foco está en el centro de la Tierra
donde el ángulo θ se mide desde el perigeo, sin embargo el punto de lanzamiento está en el apogeo, θ=π.
Creamos un script para dibujar una órbita elíptica situada en un plano que hace un ángulo λ con el plano XY. Se dibuja el punto A de lanzamiento, el vector velocidad inicial v0 y el punto P de impacto en la intersección de la órbita elíptica (en rojo) con la superficie esférica de la Tierra (en azul).
Poniendo en la ecuación de la trayectoria r=R. El ángulo θ0 que forma la dirección del punto de lanzamiento con la de impacto es
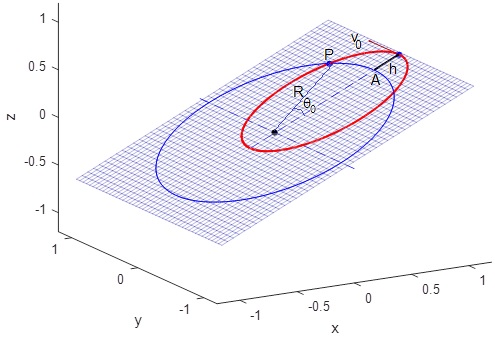
La posición del punto de impacto en la intersección de la órbita elíptica con la superficie esférica de la Tierra es
Para dibujar una parte de la figura se ha empleado el siguiente código
%plano de la órbita
lambda=pi/6;
[x,y]=meshgrid(-1.1:0.05:1.1,-1.1:0.05:1.1);
z=x*tan(lambda);
hold on
h1=mesh(x,y,z);
set(h1,'EdgeColor',[0,0,0.6],'EdgeAlpha',0.3,'FaceAlpha',0.3)
th=(1:360)*pi/180;
r1=0.25; r2=1.25; %órbita elíptica
ex=(r2-r1)/(r2+r1);
p=r1*(1+ex);
x=-p*cos(th)./(1+ex*cos(th));
y=p*sin(th)./(1+ex*cos(th));
z=zeros(1,length(x));
X=x*cos(lambda)-z*sin(lambda);
Z=x*sin(lambda)+z*cos(lambda);
plot3(X,y,Z,'r','lineWidth',1.5);
plot3(0,0,0,'ko','markersize',4,'markeredgecolor','k','markerfacecolor','k');
line([0,0],[-1.2,1.2],[0,0],'lineStyle','--','color','b')
line([-r1*cos(lambda),r2*cos(lambda)],[0,0],[-r1*sin(lambda),r2*sin(lambda)],
'lineStyle','--','color','b')
%tierra
R=1;
x=R*cos(th);
y=R*sin(th);
z=zeros(1,length(x));
X=x*cos(lambda)-z*sin(lambda);
Z=x*sin(lambda)+z*cos(lambda);
plot3(X,y,Z,'b');
%intersección
th_0=acos((p-R)/(ex*R));
z=0;
X=R*cos(pi-th_0)*cos(lambda)-z*sin(lambda);
Z=R*cos(pi-th_0)*sin(lambda)+z*cos(lambda);
y=R*sin(pi-th_0);
plot3(X,y,Z,'bo','markersize',4,'markeredgecolor','b','markerfacecolor','b');
%lanzamiento
line([R*cos(lambda),r2*cos(lambda)],[0,0],[R*sin(lambda),r2*sin(lambda)],
'color','k', 'lineWidth',1.5)
x=r2*cos(lambda);
z=r2*sin(lambda);
plot3(x,0,z,'bo','markersize',4,'markeredgecolor','b','markerfacecolor','b');
h1=quiver3(x,0,z,0,0.5,0);
set(h1,'Color',[0.7,0,0])
view(-30,20)
ylim([-1.2,1.2])
xlim([-1.2,1.2])
zlim([-1.2,1.2])
hold off
xlabel('x'); ylabel('y'); zlabel('z')
title('Desviación')
Tiempo de vuelo
Calculamos el instante de impacto empleando la ecuación de Kepler
- Se calcula el tiempo t0 para posición angular π-θ0
- Se calcula el tiempo t1 para posición π
Dada la posición angular θ, determinamos el ángulo E mediante las relaciones
Dependiendo del signo del seno y del coseno, se determina el cuadrante y se calcula el ángulo E. Sustituyendo en la ecuación de Kepler, obtenemos Me
Conocido Me, obtenemos el tiempo τ hasta que impacta en la superficie de la Tierra
Una partícula se deja caer desde lo alto de una torre de h=10 km de altura que está situada en la latitud λ=30°
R=6.378e6; %radio Tierra
M=5.98e24; %masa de la Tierra
G=6.67e-11; %constante G
r1=R+10000; %distancia al centro de la Tierra, 10 km de altura
lambda=pi/6; %latitud 30°
w=2*pi/(24*60*60); %velocidad angular de rotación de la Tierra
L=r1*w*r1*cos(lambda); %momento angular
d=L^2/(G*M);
E=(w*r1*cos(lambda))^2/2-G*M/r1; %energía
ex=sqrt(1+2*L^2*E/(G*M)^2); %excentricidad
a=d/(1-ex^2); %semieje mayor de la elipse
angulo=acos((d-R)/(R*ex));
th=angulo; %posición inicial
c_E=(ex+cos(th))/(1+ex*cos(th));
s_E=sqrt(1-ex^2)*sin(th)/(1+ex*cos(th));
E=atan2(s_E,c_E);
if E<0
E=2*pi+E;
end
t0=(E-ex*s_E)*a^(3/2)/sqrt(G*M);
th=pi; %posición final
c_E=(ex+cos(th))/(1+ex*cos(th));
s_E=sqrt(1-ex^2)*sin(th)/(1+ex*cos(th));
E=atan2(s_E,c_E);
if E<0
E=2*pi+E;
end
t1=(E-ex*s_E)*a^(3/2)/sqrt(G*M);
tau=t1-t0;
fprintf('El tiempo de vuelo (s) es %2.3f\n',tau)
El tiempo de vuelo (s) es 45.281
El tiempo que tarda en impactar en la superficie de la Tierra es τ=45.3 s
Sistema de Referencia Inercial
En el tiempo τ la torre se ha movido a lo largo del paralelo de A a B, un ángulo ωτ. La latitud de la base de la torre es λ y la longitud ωτ (tomando como referencia el meridiano que pasa por la posición inicial). El vector posición de la base de la torre es
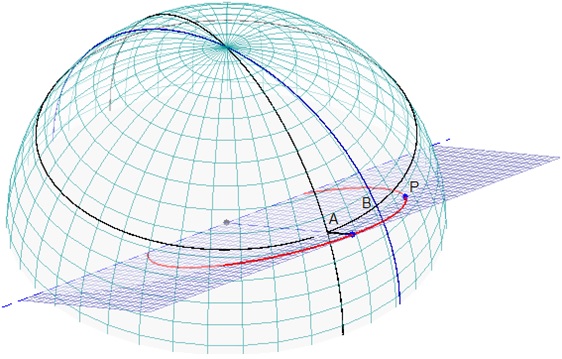
Como vemos en la figura, la partícula se deja caer desde lo alto de la torre de altura h, cuya base está A a una latitud λ. La partícula describe un arco de elipse hasta que impacta en P con la superficie de la tierra empleando un tiempo τ. Mientras tanto, la base de la torre se ha desplazado a B a lo largo del paralelo un ángulo ωτ
Para dibujar una parte de la figura se ha empleado el siguiente código
%esfera
R=1;
phi=linspace(0,pi,30);
theta=linspace(0,2*pi,40);
[phi,theta]=meshgrid(phi,theta);
x=R*sin(phi).*cos(theta);
y=R*sin(phi).*sin(theta);
z=R*cos(phi);
h1=mesh(x,y,z);
set(h1,'EdgeColor',[0.,0.6,0.6],'EdgeAlpha',0.5,'FaceAlpha',0.5);
%meridiano
phi=0;
theta=-pi:0.1:pi;
x=sin(theta)*cos(phi);
y=sin(theta)*sin(phi);
z=cos(theta);
h1=line(x,y,z);
set(h1,'Color',[0,0,0],'LineWidth',1)
%meridiano
phi=20*pi/180;
x=sin(theta)*cos(phi);
y=sin(theta)*sin(phi);
z=cos(theta);
h1=line(x,y,z);
set(h1,'Color',[0,0,0.7],'LineWidth',1)
%paralelo
lambda=pi/6;
phi=0:0.1:2*pi;
x=cos(lambda)*cos(phi);
y=cos(lambda)*sin(phi);
z=sin(lambda)*ones(1,length(x));
h1=line(x,y,z);
set(h1,'Color',[0,0,0],'LineWidth',1)
%plano de la órbita
lambda=pi/6;
[x,y]=meshgrid(-1.1:0.05:1.1,-1.1:0.05:1.1);
z=x*tan(lambda);
hold on
h1=mesh(x,y,z);
set(h1,'EdgeColor',[0,0,0.6],'EdgeAlpha',0.3,'FaceAlpha',0.3)
th=(1:360)*pi/180;
r1=0.25; r2=1.25; %órbita elíptica
ex=(r2-r1)/(r2+r1);
p=r1*(1+ex);
x=-p*cos(th)./(1+ex*cos(th));
y=p*sin(th)./(1+ex*cos(th));
z=zeros(1,length(x));
X=x*cos(lambda)-z*sin(lambda);
Z=x*sin(lambda)+z*cos(lambda);
plot3(X,y,Z,'r','lineWidth',1.5);
plot3(0,0,0,'ko','markersize',4,'markeredgecolor','k','markerfacecolor','k');
line([0,0],[-1.2,1.2],[0,0],'lineStyle','--','color','b')
line([-r1*cos(lambda),r2*cos(lambda)],[0,0],[-r1*sin(lambda),r2*sin(lambda)],
'lineStyle','--','color','b')
%intersección
th_0=acos((p-R)/(ex*R));
z=0;
X=R*cos(pi-th_0)*cos(lambda)-z*sin(lambda);
Z=R*cos(pi-th_0)*sin(lambda)+z*cos(lambda);
y=R*sin(pi-th_0);
plot3(X,y,Z,'bo','markersize',4,'markeredgecolor','b','markerfacecolor','b');
%lanzamiento
line([R*cos(lambda),r2*cos(lambda)],[0,0],[R*sin(lambda),r2*sin(lambda)],'color'
,'k', 'lineWidth',1.5)
x=r2*cos(lambda);
z=r2*sin(lambda);
plot3(x,0,z,'bo','markersize',4,'markeredgecolor','b','markerfacecolor','b');
axis equal
axis off
zlim([0,1])
view(58,37)
hold off
xlabel('x'); ylabel('y'); zlabel('z')
title('Desviación')
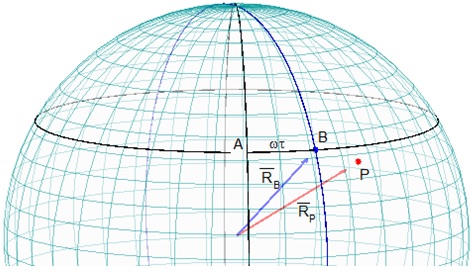
Conocidos los vectores , calculamos la posición relativa de P respecto de B, el vector diferencia
Para dibujar parte de esta figura se ha empleado el siguiente código
%esfera
hold on
R=1;
phi=linspace(0,pi,30);
theta=linspace(0,2*pi,40);
[phi,theta]=meshgrid(phi,theta);
x=R*sin(phi).*cos(theta);
y=R*sin(phi).*sin(theta);
z=R*cos(phi);
h1=mesh(x,y,z);
set(h1,'EdgeColor',[0.,0.6,0.6],'EdgeAlpha',0.5,'FaceAlpha',0.5);
%meridiano
phi=0;
theta=-pi:0.1:pi;
x=sin(theta)*cos(phi);
y=sin(theta)*sin(phi);
z=cos(theta);
h1=line(x,y,z);
set(h1,'Color',[0,0,0],'LineWidth',1)
%paralelo
lambda=pi/6;
phi=0:0.1:2*pi;
x=cos(lambda)*cos(phi);
y=cos(lambda)*sin(phi);
z=sin(lambda)*ones(1,length(x));
h1=line(x,y,z);
set(h1,'Color',[0,0,0],'LineWidth',1)
%meridiano, base torre
phi=20*pi/180;
x=sin(theta)*cos(phi);
y=sin(theta)*sin(phi);
z=cos(theta);
h1=line(x,y,z);
plot3(R*cos(lambda)*cos(phi),R*cos(lambda)*sin(phi),R*sin(lambda),
'bo','markersize',4,'markeredgecolor','b','markerfacecolor','b');
set(h1,'Color',[0,0,0.7],'LineWidth',1)
h1=quiver3(0,0,0,R*cos(lambda)*cos(phi),R*cos(lambda)*sin(phi),R*sin(lambda));
set(h1,'Color',[0,0,1],'lineWidth',1.5)
%intersección
th_0=acos((p-R)/(ex*R));
z=0;
X=R*cos(pi-th_0)*cos(lambda)-z*sin(lambda);
Z=R*cos(pi-th_0)*sin(lambda)+z*cos(lambda);
y=R*sin(pi-th_0);
plot3(X,y,Z,'ro','markersize',4,'markeredgecolor','r','markerfacecolor','r');
h1=quiver3(0,0,0,X,y,Z);
set(h1,'Color',[1,0,0],'lineWidth',1.5)
axis equal
axis off
view(87,9)
hold off
xlabel('x'); ylabel('y'); zlabel('z')
title('Vectores')
Sistema de Referencia Local
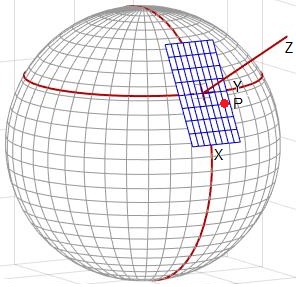
En la figura se muestra el plano local, el eje Z sigue la dirección radial, el eje X es tangente al meridiano del lugar y el eje Y es tangente al paralelo del lugar. Las coordenadas del punto de impacto P en este Sistema de Referencia Local son las desviaciones hacia el este e y hacia el sur s, que vamos a calcular a continuación
Hemos calculado las componentes del vector , referidas al Sistema de Referencia Inercial OXYZ son:
Tenemos que calcular sus componentes de este vector en el Sistema de Referencia Local BX''Y''Z'', para ello tenemos que realizar dos transformaciones:
Giramos el Sistema OXYZ alrededor del eje Z un ángulo ωτ
Giramos el sistema OX'Y'Z' alrededor del eje Y' un ángulo π/2-λ
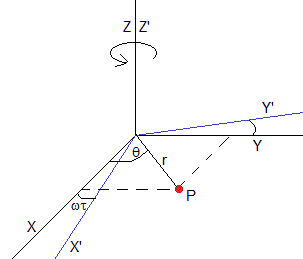
Las componentes (x,y,z) de de P respecto del Sistema de Referencia OXYZ están relacionadas con las componentes (x',y',z') de P respecto del Sistema de Referencia OX'Y'Z' del siguiente modo
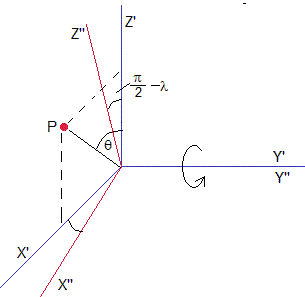
Las componentes (x',y',z') de de P respecto del Sistema de Referencia OX'Y'Z' están relacionadas con las componentes (x'',y'',z'') de P respecto del Sistema de Referencia OX''Y''Z'' del siguiente modo
El resultado de las dos transformaciones para las dos primeras componentes (x'', y'') del punto P en las que estamos interesados es
x'' es la componente X de P en el Sistema de Referencia Local y corresponde a la desviación hacia el Sur, s
y'' es la componente Y de P en el Sistema de Referencia Local y corresponde a la desviación hacia el Este, e
Cuando dejamos caer la partícula desde lo alto de una torre situada en el plano ecuatorial, λ=0, no se desvía hacia el sur s=0.
Completamos el script que nos calculaba el tiempo τ de impacto, para determinar las desviaciones e y s de la partícula
Calculamos el tiempo de vuelo, la desviación hacia el este y hacia el sur de una partrícula que se deja caer desde el alto de una torre de h=100 m de altura, situada en la latitud λ=45°
R=6.378e6; %radio Tierra
M=5.98e24; %masa de la Tierra
G=6.67e-11; %constante G
r1=R+100; %distancia al centro de la Tierra, 1000 m
lambda=pi/4; %latitud
w=2*pi/(24*60*60); %velocidad angular de rotación de la Tierra
L=r1*w*r1*cos(lambda); %momento angular
d=L^2/(G*M);
E=(w*r1*cos(lambda))^2/2-G*M/r1; %energía
ex=sqrt(1+2*L^2*E/(G*M)^2); %excentricidad
a=d/(1-ex^2); %semieje mayor de la elipse
angulo=acos((d-R)/(R*ex));
th=angulo; %posición inicial
c_E=(ex+cos(th))/(1+ex*cos(th));
s_E=sqrt(1-ex^2)*sin(th)/(1+ex*cos(th));
E=atan2(s_E,c_E);
if E<0
E=2*pi+E;
end
t0=(E-ex*s_E)*a^(3/2)/sqrt(G*M);
th=pi; %posición final
c_E=(ex+cos(th))/(1+ex*cos(th));
s_E=sqrt(1-ex^2)*sin(th)/(1+ex*cos(th));
E=atan2(s_E,c_E);
if E<0
E=2*pi+E;
end
t1=(E-ex*s_E)*a^(3/2)/sqrt(G*M);
tau=t1-t0;
fprintf('El tiempo de vuelo (s) es %2.3f\n',tau)
e=R*(sin(pi-angulo)*cos(w*tau)-cos(lambda)*cos(pi-angulo)*sin(w*tau));
s=R*sin(lambda)*(cos(pi-angulo)*cos(w*tau)*cos(lambda)+sin(pi-angulo)*sin(w*tau)
-cos(lambda)-cos(pi-angulo)+1);
fprintf('Desviación hacia el este %2.4f, hacia el sur %2.4f\n',e,s)
El tiempo de vuelo (s) es 4.520 Desviación hacia el este 0.0155, hacia el sur 0.2080
El tiempo de vuelo es aproximadamente
La torre desde la que se deja caer la partícula, no tiene la dirección radial, sino dirección vertical del lugar, lo que implica una corrección en la desviación hacia el sur
Desviación hacia el este, cálculo aproximado
La aceleración se expresa en coordenadas polares,
En el Sistema de Referencia Inercial, la única fuerza que actúa sobre la partícula es mg0. Donde g0 es la aceleración de la gravedad en la superficie de la Tierra, cuya dirección es radial y sentido hacia el centro de la Tierra
Las ecuaciones del movimiento son
La segunda ecuación expresa la constancia del momento angular en coordenadas polares
El momento angular es constante e igual al momento angular inicial. Si la distancia inicial de la partícula a la superficie de la Tierra es h y se encuentra a una latitud λ
x es la distancia de la partícula a la superficie de la Tierra. Se ha tenido en cuenta que h/R<<1
La ecuación del movimiento en la dirección radial se expresa
Combinando la aceleración g0 con la aceleración centrífuga tenemos la aceleración efectiva g que supondremos que es aproximadamente constante. Para un movimiento rectilíneo con aceleración constante
Sustituyendo x en la ecuación de la constancia del momento angular
El primer término es el desplazamiento angular de la base de la torre, por lo que el desplazamiento de la partícula referido a la base de la torre es
La longitud del arco, o desplazamiento δS hacia el este es
Casos particulares
Se deja caer la partícula desde una altura h, v0=0
Se lanza la partícula con velocidad inicial v0 desde la superficie de la Tierra, h=0.
Se lanza desde una altura h con velocidad inicial v0
Para una partícula que se deja caer desde una altura de h=100 m en el hemisferio norte a una latitud λ=45°, δS=1.55 cm
El tiempo que tarda en regresar al suelo es t=v0/g
Lo que indica que la partícula se desvía hacia el oeste.
Para una partícula que se lanza con velocidad inicial de v0=30 m/s, la desviación hacia el oeste es δS=-1.92 cm
El tiempo que tarda una partícula que parte desde una altura h con velocidad inicial v0 en regresar al suelo x=0 es
para que la desviación δS=0, sea cero se tiene que cumplir
Una partícula que se lanza desde una altura h=100 m con la velocidad inicial v0=25.6 m/s, cae en el mismo punto de lanzamiento, δS=0. Esta velocidad es independiente de la latitud.
Referencias
J. M. Potgieter. An exact solution for the horizontal defection of a falling object. Am. J. Phys. 5183) march 1983, pp. 257-258
Elie Belorizki, Jean Sivardière. Comments on the horizontal defection of a falling object. Am. J. Phys. 55(12) December 1987, pp. 1103-1104
Del último apartado: Desviación hacia el este, cálculo aproximado
Pirooz Mohazzabi. Free fall and angular momentum. Am. J. Phys. 67(11) November 1999, pp. 1017-1020

