El mejor ángulo para arrastrar un bloque

En esta página, se presenta un ejemplo más en el que se analiza la fuerza de rozamiento entre un cuerpo y la superficie horizontal sobre la que desliza. La novedad de este ejemplo, es que la reacción del plano no es constante sino que cambia con el ángulo que forma la fuerza aplicada con la horizontal.

Sea un bloque rectangular de masa m que está situado sobre un plano horizontal. Si aplicamos una fuerza T que hace un ángulo θ con la horizontal, ¿cuál debe ser el valor de dicha fuerza para que el bloque empiece a moverse?. Más aún, determínese el valor del ángulo θ para el cual la fuerza aplicada es mínima.

Habitualmente, los estudiantes tienden a identificar la reacción del plano o la fuerza normal N hacia arriba que ejerce el plano sobre el bloque, con el peso mg si el plano es horizontal, y con la componente perpendicular del peso mgcosθ si el plano está inclinado un ángulo θ. Vamos a ver en este ejemplo, que el valor de la reacción del plano N depende de las otras fuerzas que se aplican sobre el bloque.

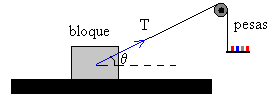
En la primera parte de esta página, se analiza la situación de equilibrio, mientras el bloque está en reposo sobre el plano horizontal. En la página titulada La máquina de Atwood y sus variantes, se describe el movimiento vertical de las pesas y del bloque sobre el plano horizontal una vez que ha empezado a deslizar. Veremos que, debido a la geometría, un problema aprentemente sencillo, conduce a una ecuación diferencial del movimiento bastante complicada, que es preciso resolver aplicando procedimientos numéricos

Estática

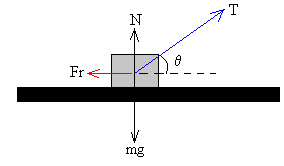
Dibujamos las fuerzas que actúan sobre el bloque

El peso mg
La fuerza aplicada T que forma un ángulo θ con la horizontal.
La fuerza N que ejerce el plano sobre el bloque
La fuerza de rozamiento F_r.

Las condiciones de equilibrio se escriben

Tcosθ-F_r=0
Tsinθ+N-mg=0

Cuando el bloque empieza a deslizar la fuerza de rozamiento alcanza un valor máximo dado por F_r=μ_sN, siendo μ_sel coeficiente de rozamiento estático, y N=mg-Tsinθ

En esta situación, despejamos T del sistema de ecuaciones.

$T = \frac{μ_{s} m g}{\cos θ + μ_{s} \sin θ}$

T es una función del ángulo θ que representamos gráficamente

m=1; %masa bloque
mu=0.7; %coeficiente estático
f=@(x) mu*m*9.8./(cos(x*pi/180)+mu*sin(x*pi/180)); %fuerza
fplot(f,[0,90])
ylim([0,10])
ang=atan(mu)*180/pi;
line([ang,ang],[0, mu*m*9.8/sqrt(1+mu^2)],'linestyle','--');
ylabel('T (N)')
xlabel('\theta')
grid on
title('Fuerza T')

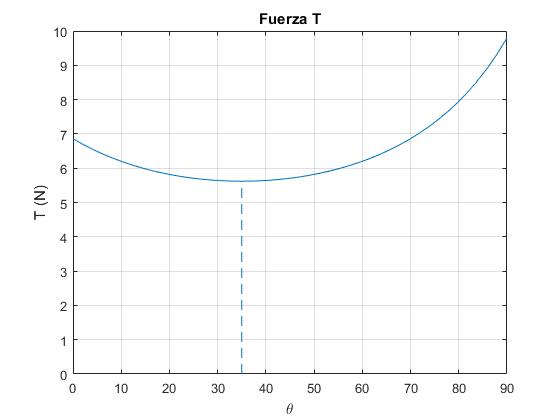
Para θ=0, T=μ_smg
Para θ=π/2, T=mg
Esta función tiene un mínimo, el mejor ángulo para arrastrar el bloque, que se obtiene derivando T respecto de θ, e igualando a cero.

$\frac{d T}{d θ} = \frac{- μ_{s} m g (- \sin θ + μ_{s} \cos θ)}{{(\cos θ + μ_{s} \cos θ)}^{2}} = 0$

El valor de la fuerza mínima T que tenemos que aplicar al cuerpo para que empiece a deslizar vale

$\tan θ = μ_{s} T_{\min} = \frac{μ_{s} m g}{\sqrt{1 + μ_{s}^{2}}}$

Actividades

Se introduce

El coeficiente estático μ_s, en el control titulado Coeficiente de rozamiento
El ángulo que forma la cuerda con la horizontal, en el control titulado Angulo
La masa m del bloque que está sobre el plano horizontal se ha fijado en 1 kg.

Se pulsa el botón titulado Nuevo

Aplicamos la fuerza T colocando pesas en el extremo de la cuerda que pasa por la polea, para ello, se selecciona el tipo de pesa y se arrastra con el puntero del ratón hasta colgarla del gancho, o de la pesa previa.

Tenemos que acercarnos lo máximo posible al valor de la fuerza μ_sN que hace que el bloque comience a deslizar con el juego de pesas disponible. En este caso, se dispone de un total de 16 pesas, cuatro de cada tipo:

5
25 g
100 g
500 g

Ejemplo:

μ_s=0.75
θ=30º

Procedimiento para acercarnos al valor máximo de la fuerza de rozamiento.

Se empieza colocando una pesa de 500 g, el bloque no desliza. Se pone una segunda pesa de 500 g, el bloque desliza.
Se pulsa el botón titulado Repetir. Se pone una pesa de 500 g. Se añade una pesa de 100 g, el bloque no desliza. Se añade otra pesa de 100 g, el bloque desliza.
Se pulsa el botón titulado Repetir. Se pone una pesa de 500 g, y una pesa de 100 g. Se añade una pesa de 25 g, el bloque desliza.
Se pulsa el botón titulado Repetir. Se pone una pesa de 500 g, una pesa de 100 g. Se añade una pesa de 5 g, el bloque desliza.

El valor de la tensión T de la cuerda más cercana al valor máximo μ_sN (por exceso) es

$T = \frac{(500 + 100 + 5) 10.0}{1000} = 6.05 N$

La aceleración de la gravedad se ha tomado como g=10.0 m/s²

En la parte superior izquierda, se dibujan las fuerzas sobre el bloque. Observamos que la fuerza N que ejerce el plano sobre el bloque no es constante e igual al peso del bloque mg sino que va cambiando a medida que se modifica la fuerza aplicada T o el ángulo θ que hace la cuerda con la horizontal.

Coeficiente de rozamiento:
Angulo:

La fuerza de rozamiento

Dada la fuerza T o bien f=T/mg se pueden producir los siguientes casos:

mu=0.6; %coeficiente estático
f=@(x) mu./(cos(x*pi/180)+mu*sin(x*pi/180)); %fuerza
fplot(f,[0,90], 'lineWidth',1.5)
ylim([0,1.5])
ang=atan(mu)*180/pi;
line([ang,ang],[0, mu/sqrt(1+mu^2)],'linestyle','--');
line([0,90],[0.3,0.3],'color','r')
line([0,90],[mu/sqrt(1+mu^2),mu/sqrt(1+mu^2)],'color','r')
line([0,90],[0.55,0.55],'color','r')
line([0,90],[0.75,0.75],'color','r')
line([0,90],[1.2,1.2],'color','r')
ylabel('T/mg')
xlabel('\theta')
grid on
title('Fuerza T/mg')

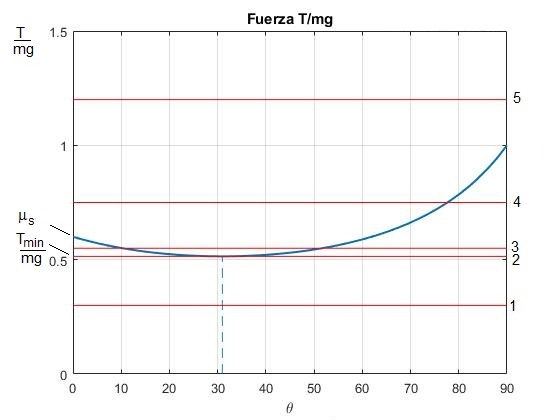
T<T_min. No hay ningún punto de intersección
T=T_min. Hay un punto de intersección, tanθ=μ_s
T_min<T<μ_smg. Tenemos dos puntos de intersección que corresponden a los ángulos θ₁ y θ₂
μ_smg<T<mg. Tenemos un punto de intersección que corresponde al ángulo θ₂, θ₁=0
T>mg. θ₁=0, θ₂ corresponde al ángulo para el que la reacción del plano horizontal N es nula

Las fuerzas que actúan sobre el bloque son:

El peso mg
La fuerza aplicada T que forma un ángulo θ con la horizontal.
La fuerza N que ejerce el plano sobre el bloque
La fuerza de rozamiento F_r.

Las condiciones de equilibrio se escriben

Tcosθ-F_r=0
Tsinθ+N-mg=0

Dado el valor de la fuerza aplicada T, calculamos la fuerza de rozamiento F_ry la fuerza N que ejerce el plano sobre el bloque:

N=mg-Tsinθ

La reacción N de la superficie horizontal se anula, es decir, el cuerpo se eleva sobre la superficie, si Tsinθ≥mg. Si N>0 la fuerza de rozamiento F_r tiene uno u otro de los siguientes valores:

Si T·cosθ <μ_s(mg-Tsinθ), el cuerpo está en equilibrio en reposo, F_r=T·cosθ
Si T·cosθ ≥μ_s(mg-Tsinθ), el cuerpo desliza y F_r=μ_k(mg-Tsinθ)

Siendo μ_s el coeficiente estático.

Designando f=T/(mg), calculamos los ángulos θ para los cuales las curvas f·cosθ y μ_s(1-f·sinθ) se cortan.

f·cosθ =μ_s(1-f·sinθ)

Primero se divide por cosθ, a continuación se emplea la relación 1/cos²θ=1+tan²θ. Quedando la siguiente ecuación en x=tanθ.

$μ_{s} \sqrt{1 + x^{2}} = f + μ_{s} f x$

Elevando al cuadrado ambos miembros, nos queda una ecuación de segundo grado cuyas soluciones son

$\tan θ = x = \frac{- f^{2} \pm \sqrt{μ_{s}^{2} f^{2} + f^{2} - μ_{s}^{2}}}{μ_{s} (f^{2} - 1)}$

Pueden ocurrir los siguientes casos:

No hay raíces reales cuando el discriminante es negativo, es decir, cuando T<T_min

$f < \frac{μ_{s}}{\sqrt{1 + μ_{s}^{2}}}$

Sea μ_s=0.6 y f=0.5,

mu_s=0.6; %coeficiente estático
f=0.5; %fuerza

hold on
fplot(@(t) f*cos(t),[0,pi/2])
fplot(@(t) mu_s*(1-f*sin(t)),[0,pi/2])
hold off
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
grid on
xlabel('\theta')
ylabel('f')
legend('fcos(\theta)','\mu_s(1-fsin(\theta))')
title('Fuerza de rozamiento')

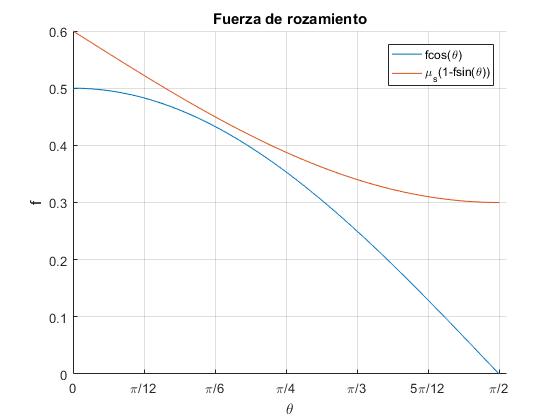
Observamos, que la función μ_s(1-f·sinθ) se mantiene por encima f·cosθ, el cuerpo siempre está en reposo y la fuerza de rozamiento vale f_r= f·cosθ

Cuando el discriminante es nulo, es decir, cuando T=T_min

$f = \frac{μ_{s}}{\sqrt{1 + μ_{s}^{2}}}$

La raíz doble de la ecuación de segundo grado vale

tanθ=μ_s

Que corresponden a la fuerza T_min=f·mg y ángulo óptimo para arrastrar el bloque, deducido en el primer apartado

Sea μ_s=0.6, calculamos el valor de f=0.514

mu_s=0.6; %coeficiente estático
f=mu_s/sqrt(1+mu_s^2); %fuerza
th=atan(mu_s); 
fprintf('Angulo: %1.2f\n',th*180/pi)

hold on
fplot(@(t) f*cos(t),[0,pi/2])
fplot(@(t) mu_s*(1-f*sin(t)),[0,pi/2])
line([th,th],[0,f*cos(th)],'lineStyle','--')
hold off
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
grid on
xlabel('\theta')
ylabel('f')
legend('fcos(\theta)','\mu_s(1-fsin(\theta))')
title('Fuerza de rozamiento')

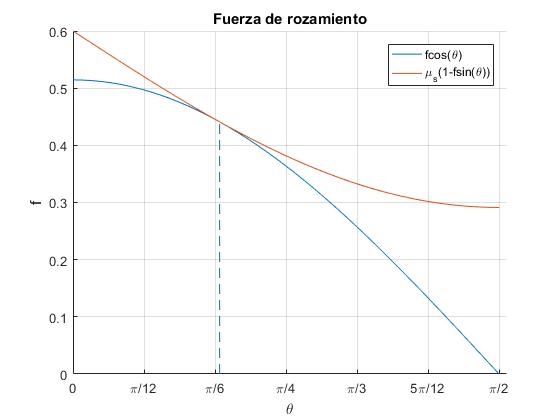
Angulo: 30.96

Observamos, que la función μ_s(1-f·sinθ) se mantiene por encima de f·cosθ, tocándose para el ángulo θ=31º. El cuerpo está en reposo, la fuerza de rozamiento vale f_r= f·cosθ. Justamente para este único ángulo el cuerpo empieza a deslizar y la fuerza de rozamiento disminuye al valor μ_k(1-f·sinθ)

T_min<T<μ_smg y μ_smg<T<mg. Tenemos dos raíces x₁ y x₂ que corresponden a los ángulos θ₁ y θ₂

Sea μ_s=0.6, e incrementamos la fuerza f=0.55. Probar tambien con f=0.7

mu_s=0.6; %coeficiente estático
mu_k=0.5; %coeficiente cinético
f=0.55; %fuerza

hold on
fplot(@(t) f*cos(t),[0,pi/2])
fplot(@(t) mu_s*(1-f*sin(t)),[0,pi/2])
discriminante=(f*mu_s)^2+f^2-mu_s^2;
if discriminante>=0
    th_1=atan((-f^2+sqrt(discriminante))/(mu_s*(f^2-1)));
    if th_1<0
        th_1=0;
    end
    th_2=atan((-f^2-sqrt(discriminante))/(mu_s*(f^2-1)));
    fprintf('Angulos: %1.2f, %1.2f\n',th_1*180/pi,th_2*180/pi)
    fr=@(t) f*(t<th_1).*cos(t)+mu_k*((t>=th_1)&(t<=th_2)).
*(1-f*sin(t))+f*(t>th_2).*cos(t);
    fplot(fr,[0,pi/2],'color','k')
    line([th_1,th_1],[0,fr(th_1)],'lineStyle','--')
    line([th_2,th_2],[0,fr(th_2)],'lineStyle','--')
end
hold off
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
grid on
xlabel('\theta')
ylabel('f')
legend('fcos(\theta)','\mu_s(1-fsin(\theta))','f_r')
title('Fuerza de rozamiento')

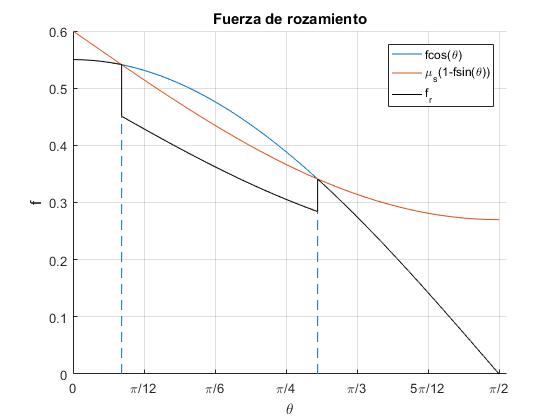
Angulos: 10.26, 51.66

Calculamos las raíces de la ecuación de segundo grado x₁ y x₂ y los ángulos correspondientes θ₁=10.26 y θ₂=51.66,

En la región 0< θ< θ₁

f·cosθ es menor que μ_s(1-f·sinθ), el cuerpo permanece en reposo y la fuerza de rozamiento es f_r= f·cosθ

En la región θ₁≤ θ≤ θ₂

f·cosθ es mayor que μ_s(1-f·sinθ), el cuerpo desliza y la fuerza de rozamiento f_r disminuye al valor μ_k(1-f·sinθ)

En la región θ₂< θ< 90º

f·cosθ es menor que μ_s(1-f·sinθ), el cuerpo permanece en reposo y la fuerza de rozamiento vale f_r= f·cosθ

Por tanto, en el intervalo angular (θ₁≤ θ≤ θ₂) el cuerpo desliza, para el resto de los ángulos el cuerpo permanece en reposo.

T>mg. Entonces θ₁=0,

Sea μ_s=0.6, e incrementamos la fuerza f=1.2

En este caso, la reacción del plano horizontal N tal que N+Tsinθ=mg o bien, N/mg=1-fsinθ, se hace cero para el ángulo sinθ₂=1/f. Para este ángulo, el bloque deja de estar en contacto con el plano horizontal

mu_s=0.6; %coeficiente estático
mu_k=0.5; %coeficiente cinético
f=1.2; %fuerza

hold on
fplot(@(t) f*cos(t),[0,pi/2])
fplot(@(t) mu_s*(1-f*sin(t)),[0,pi/2])
th_1=0;
th_2=asin(1/f);
fprintf('Angulos: %1.2f, %1.2f\n',th_1*180/pi,th_2*180/pi)
fr=@(t) mu_k*(1-f*sin(t));
fplot(fr,[0,th_2],'color','k')
hold off
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
grid on
xlabel('\theta')
ylabel('f')
legend('fcos(\theta)','\mu_s(1-fsin(\theta))','f_r')
title('Fuerza de rozamiento')

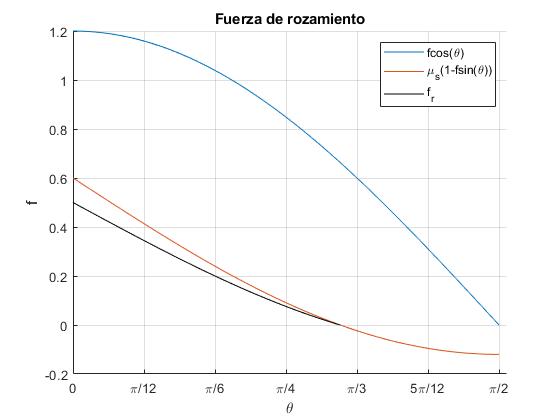
Angulos: 0, 56.44

Referencias

Sütt D. Elementary discussion of an optimization problem concerning friction. Physics Education 29 (4) July 1994, 249-252

van den Berg W. The best angle for dragging a box. The Physics Teacher, Vol. 38 Nov. 2000, pp. 506-508