Rozamiento en el plano inclinado

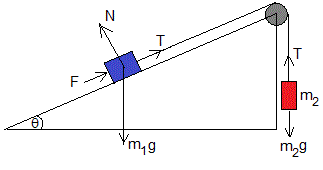
Las fuerzas que actúan sobre el cuerpo de masa m₂ son:

El peso, m₂g
La tensión T de la cuerda

Las fuerzas que actúan sobre el cuerpo de masa m₁ son:

El peso, m₁g
La tensión T de la cuerda
La reacción N del plano inclinado
La fuerza de rozamiento F entre el cuerpo y el plano inclinado

Cuando el cuerpo está en movimiento, F es opuesta a su velocidad y vale F=μ_kN. Siendo μ_k el coeficiente cinético
Cuando el cuerpo está en reposo, F es opuesta a la resultante a lo largo del plano inclinado, de las fuerzas que actúan sobre el cuerpo, T-m₁gsinθ. F no puede ser mayor en módulo que μ_sN. Siendo μ_s el coeficiente estático

El equilibrio en el sentido perpendicular al plano inclinado, implica que N=m₁gcosθ

Cuerpos en reposo

Cuando los cuerpos están en equilibrio, en reposo, la tensión de la cuerda T=m₂g

Si m₂g>m₁gsinθ, (la resultante es positiva), la fuerza de rozamiento F será negativa (dirigida hacia la izquierda)
Si m₂g<m₁gsinθ, (la resultante es negativa), la fuerza de rozamiento F será positiva (dirigida hacia la derecha), tal como se muestra en la figura
El módulo de F no puede superar el valor, μ_sm₁gcosθ

Vamos a calcular el ángulo o los ángulos θ_s del plano inclinado para los cuales el módulo de la fuerza de rozamiento F alcanza su valor máximo, μ_sm₁gcosθ_s

m₂g-m₁gsinθ_s=±μ_sm₁gcosθ_s

Llamando M=m₂/m₁

$M - \sin θ_{s} = \pm μ_{s} \sqrt{1 - \sin^{2} θ_{s}}$

Elevando al cuadrado, despejamos sinθ_s

$\sin θ_{s} = \frac{M \pm μ_{s} \sqrt{1 - M^{2} + μ_{s}^{2}}}{1 + μ_{s}^{2}}$

Para que existan raíces reales el discriminante tiene que ser mayor o igual a cero

Para M<1, es decir, m₂<m₁, el discriminante es siempre positivo
Para M>1, es decir, m₂>m₁, se tiene que cumplir que

$μ_{s} \geq \sqrt{M^{2} - 1}$

Para que los dos ángulos sean positivos se tiene que cumplir además que M>μ_s

Los cuerpos en movimiento

Cuando la fuerza de rozamiento F alcanza el valor máximo μ_sm₁gcosθ, el cuerpo de masa m₁ empieza a deslizar, la fuerza de rozamiento se reduce ligeramente a μ_km₁gcosθ, opuesta a la velocidad del cuerpo. Los dos cuerpos se mueven con la misma aceleración a. Las ecuaciones del movimiento son

m₂g-T=m₂a

T-m₁gsinθ-μ_km₁gcosθ=m₁a

Eliminando la tensión T de la cuerda

$\begin{array}{l} a = \frac{m_{2} - m_{1} \sin θ - μ_{k} m_{1} \cos θ}{m_{2} + m_{1}} g \\ a = \frac{M - \sin θ - μ_{k} \cos θ}{M + 1} g \end{array}$

La tensión de la cuerda es un poco menor que el peso, T=m₂(g-a)

Ejemplos

Vamos a representar las funciones

M-sinθ, proporcional a la resultante a lo largo del plano inclinado, de las fuerzas sobre el cuerpo de masa m₁
±μ_scosθ, proporcional al valor máximo de la fuerza de rozamiento

M>1

La primera función, M-sinθ, es siempre positiva, por lo que solamente dibujamos la función μ_scosθ

M=1.1 y μ_s=0.4

El discriminante es negativo, las dos funciones no se cortan

M=1.1; %cociente m2/m1
mu_s=0.4;%coeficiente estático
 
hold on
fplot(@(t) M-sin(t),[0,pi/2])
fplot(@(t) mu_s*cos(t),[0,pi/2])
hold off
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
grid on
xlabel('\theta')
ylabel('f')
legend('M-sin(\theta)','\mu_scos(\theta)')
title('Fuerza de rozamiento')

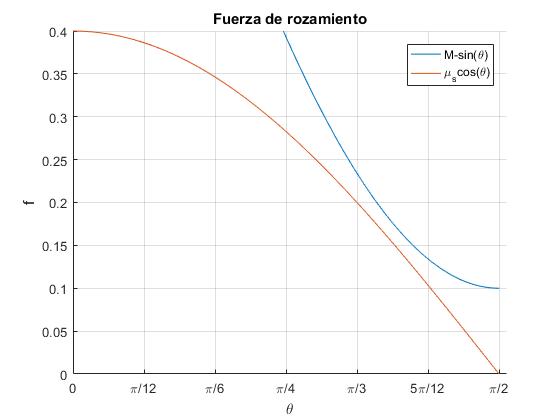
Los cuerpos aceleran para cualquier ángulo θ del plano inclinado. La fuerza de rozamiento valdrá μ_km₁cosθ, opuesta a la velocidad del cuerpo

Por ejemplo, para θ=π/6 (30°)

Resultante, m₂g-m₁gsinθ=5.88 N
Valor máximo de la fuerza de rozamiento, μ_sm₁gcosθ=3.39 N

El cuerpo acelera a lo largo del plano inclinado, hacia arriba

M=1.1 y μ_s=0.6

El discriminante es positivo, las dos funciones se cortan

M=1.1; %cociente m2/m1
mu_s=0.6;%coeficiente estático
 
hold on
fplot(@(t) M-sin(t),[0,pi/2])
fplot(@(t) mu_s*cos(t),[0,pi/2])
discriminante=1-M^2+mu_s^2;
if discriminante>=0
    th_1=asin((M+mu_s*sqrt(discriminante))/(mu_s^2+1));
    th_2=asin((M-mu_s*sqrt(discriminante))/(mu_s^2+1));
    fprintf('Angulos: %1.2f, %1.2f\n',th_1*180/pi,th_2*180/pi)
    line([th_1,th_1],[0,mu_s*cos(th_1)],'lineStyle','--')
    line([th_2,th_2],[0,mu_s*cos(th_2)],'lineStyle','--')
end
hold off
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
grid on
xlabel('\theta')
ylabel('f')
legend('M-sin(\theta)','\mu_scos(\theta)')
title('Fuerza de rozamiento')

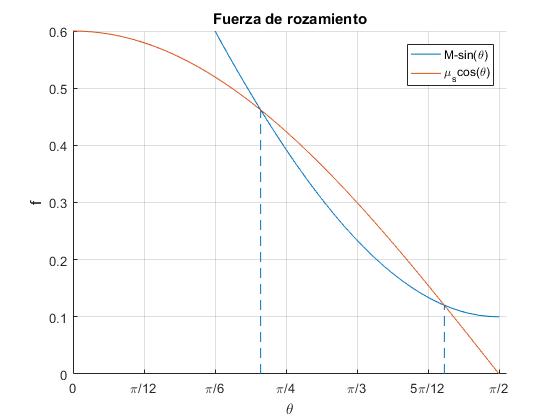
Angulos: 78.43, 39.64

Los cuerpos se mueven cuando el ángulo θ del plano inclinado está comprendido en los intervalos (0,39.64°) o (78.43°,90°). Los cuerpos están en equilibrio, en reposo, cuando el ángulo θ del plano inclinado está comprendido en el intervalo (39.64°, 78.43°)

Para θ=π/3 (60°)

Resultante, m₂g-m₁gsinθ=2.29 N
Valor máximo de la fuerza de rozamiento, μ_sm₁gcosθ=2.94 N

El cuerpo permanece en reposo, la fuerza de rozamiento que actúa sobre el cuerpo de masa m₁ es -2.29 N dirigida hacia abajo, que se opone a la resultante

M<1

M=0.6 y μ_s=0.4

El discriminante es siempre positivo, las dos funciones se cortan

Dado que la función M-sinθ, puede ser positiva o negativa, dibujamos además, la función -μ_scosθ

M=0.6;
mu_s=0.4;%coeficiente estático

hold on
fplot(@(t) M-sin(t),[0,pi/2])
fplot(@(t) mu_s*cos(t),[0,pi/2])
fplot(@(t) -mu_s*cos(t),[0,pi/2])
discriminante=1-M^2+mu_s^2;
if discriminante>=0
    th_1=asin((M+mu_s*sqrt(discriminante))/(mu_s^2+1));
    th_2=asin((M-mu_s*sqrt(discriminante))/(mu_s^2+1));
    fprintf('Angulos: %1.2f, %1.2f\n',th_1*180/pi,th_2*180/pi)
     line([th_1,th_1],[0,-mu_s*cos(th_1)],'lineStyle','--')
    line([th_2,th_2],[0,mu_s*cos(th_2)],'lineStyle','--')
end

hold off
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
grid on
xlabel('\theta')
ylabel('f')
legend('M-sin(\theta)','\mu_scos(\theta)','-\mu_scos(\theta)')
title('Fuerza de rozamiento')

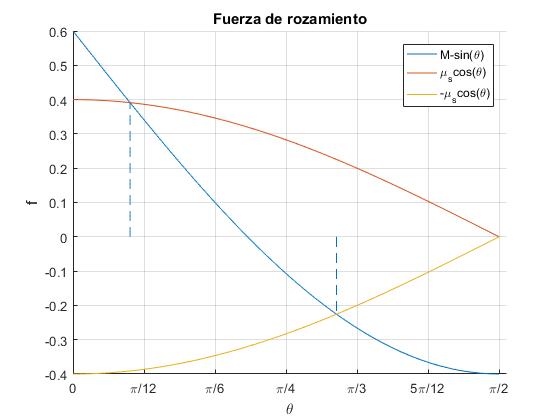
Angulos: 55.66, 12.05

Los cuerpos se mueven cuando el ángulo θ del plano inclinado está comprendido en los intervalos (0,12.05°) o (55.66°,90°). Los cuerpos están en equilibrio, en reposo, cuando el el ángulo θ del plano inclinado está comprendido en el intervalo (12.05°, 55.66°)

Para θ=10°

Resultante, m₂g-m₁gsinθ=4.18 N
Valor máximo de la fuerza de rozamiento, μ_sm₁gcosθ=3.86 N

El cuerpo de masa m₁ acelera, hacia arriba, a lo largo del plano inclinado.

Para θ=π/4 (45°)

Resultante, m₂g-m₁gsinθ=-1.05 N
Valor máximo de la fuerza de rozamiento, μ_sm₁gcosθ=2.77 N

El cuerpo permanece en reposo, la fuerza de rozamiento que actúa sobre el cuerpo de masa m₁ es 1.05 N dirigida hacia arriba, que se opone a la resultante

Para θ=π/3 (60°)

Resultante, m₂g-m₁gsinθ=-2.61 N
Valor máximo de la fuerza de rozamiento, μ_sm₁gcosθ=1.96 N

El cuerpo de masa m₁ acelera, hacia abajo, a lo largo del plano inclinado.

M=0.6 y μ_s=0.7

Comprobamos que uno de los dos ángulos es negativo, ya que M<μ_s

Actividades

Se introduce

El ángulo θ del plano inclinado, en el control titulado Angulo
La masa m₂ del cuerpo que cuelga, en el control titulado Masa
Se ha fijado la masa m₁=1 del cuerpo que descansa sobre el plano inclinado
El coeficiente estático μ_s, en el control titulado Coef. estático

El programa calcula:

La resultante de las fuerzas, a lo largo del plano inclinado, que actúan sobre el cuerpo de masa m₁, es decir, m₂g-m₁gsinθ
Valor máximo de la fuerza de rozamiento, μ_sm₁gcosθ

Cuando el módulo de la resultante es mayor que el valor máximo de la fuerza de rozamiento, el cuerpo acelera a lo largo del plano inclinado, hacia arriba o hacia abajo dependiento del signo de la resultante.

Se dibujan las fuerzas sobre el cuerpo que desliza

El peso, m₁g
La reacción N del plano inclinado
La tensión T de la cuerda
La fuerza de rozamiento una flecha de color rojo

Angulo: Masa :
Coef. estático :

Referencias

William M. Wehrbein. Frictional forces on an inclined plane. Am. J. Phys. 60 (1), January 1992, pp. 57-58