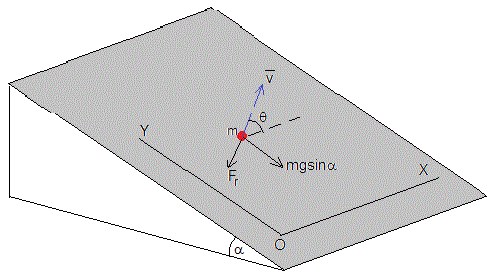
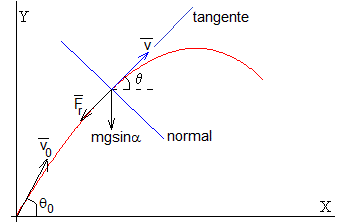
Consideremos un proyectil de masa m, que es lanzado desde el origen O con velocidad v₀ haciendo un ángulo θ₀ con el eje X. En un momento dado, la posición del proyectil es (x,y), su vector velocidad v es tangente a la trayectoria y forma un ángulo θ con el eje X.

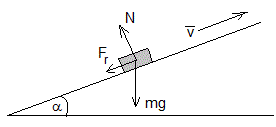
Las fuerzas que actúan sobre el proyectil son:

• el peso, mg
• la reacción del plano, N=mgcosα
• la fuerza de rozamiento F_r=μN, tiene la dirección de la velocidad y de sentido contrario

Casos particulares

Los casos particulares más sencillos se producen cuando el ángulo de tiro θ₀=π/2 y cuando θ₀=-π/2.

θ₀=π/2

${\displaystyle \begin{array}{l}a=-g\left(\sin \alpha +\mu \cos \alpha \right)\\ v=v_0+at\\ y=v_{0}t+\frac{1}{2}a{t}^2\end{array}}$

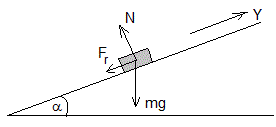
El proyectil se detiene, v=0, en la posición

${\displaystyle \begin{array}{l}x=0\\ y=\frac{1}{2}\frac{v_0^2}{g\left(\sin \alpha +\mu \cos \alpha \right)}\end{array}}$

θ₀=-π/2

${\displaystyle \begin{array}{l}a=g\left(-\sin \alpha +\mu \cos \alpha \right)\\ v=-v_0+at\\ y=-v_{0}t+\frac{1}{2}a{t}^2\end{array}}$

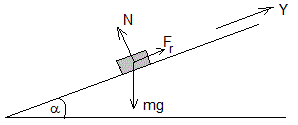
El proyectil se detiene, v=0, si μcosα>sinα, μ>tanα, en la posición

${\displaystyle \begin{array}{l}x=0\\ y=-\frac{1}{2}\frac{v_0^2}{g\left(-\sin \alpha +\mu \cos \alpha \right)}\end{array}}$

Si no se cumple esta condición, el proyectil continuará su movimiento descendente a lo largo del eje Y del plano inclinado

Movimiento general

Escribimos las ecuaciones del movimiento en la dirección tangencial y en la dirección normal

${\displaystyle \begin{array}{l}m\frac{dv}{dt}=-mg\sin \alpha \sin \theta -\mu mg\cos \alpha \\ m\frac{v^2}{\rho }=mg\sin \alpha \cos \theta \end{array}}$

donde ρ es el radio de curvatura de la trayectoria.

En el intervalo de tiempo comprendido entre t y t+dt, la dirección del vector velocidad cambia un ángulo dθ, que es el ángulo entre las tangentes o entre las normales. El móvil se desplaza en este intervalo de tiempo un arco ds=ρ·dθ, tal como se aprecia en la figura.

${\displaystyle \frac{dv}{dt}=\frac{dv}{ds}\frac{ds}{dt}=v\frac{dv}{ds}=\frac{v}{\rho }\frac{dv}{d\theta }}$

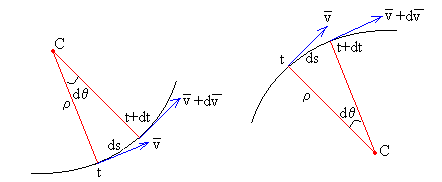
Hemos de tener en cuenta que la curvatura de la trayectoria es negativa (figura de la derecha). La curva queda a la derecha de la tangente tomada en sentido de las x crecientes. La igualdad anterior se escribe para este caso

${\displaystyle \frac{dv}{dt}=-\frac{v}{\rho }\frac{dv}{d\theta }}$

Las ecuaciones del movimiento en la dirección tangencial y en la dirección normal se convierten en una única ecuación diferencial de primer orden.

${\displaystyle \begin{array}{l}-\frac{g\sin \alpha \cos \theta }{v}\frac{dv}{d\theta }=-g\sin \alpha \sin \theta -\mu g\cos \alpha \hfill \\ \frac{1}{v}\frac{dv}{d\theta }=\tan \theta +\frac{f}{\cos \theta }\hfill \end{array}}$

Sea f=μ/tanα

• Si f>1, la fuerza de rozamiento μmgcosα será mayor que la componente del peso mgsinα y el proyectil se detendrá
• Si f≤1, el movimiento continuará sin límite

Velocidad del proyectil

Integramos la ecuación diferencial, teniendo en cuenta que en el cuerpo se lanza del origen con velocidad v₀ haciendo un ángulo θ₀ con la horizontal

${\displaystyle \begin{array}{l}{\displaystyle \underset{v_0}{\overset{v}{\int }}\frac{dv}{v}}={\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}\left(\tan \theta +\frac{f}{\cos \theta }\right)}d\theta \\ \ln \left(\frac{v}{v_0}\right)=-\ln \left(\frac{\cos \theta }{\cos {\theta }_0}\right)+f\ln \left(\frac{(1+\sin \theta )\cos {\theta }_0}{\cos \theta (1+\sin {\theta }_0)}\right)\\ v=v_0{\left(\frac{\cos {\theta }_0}{\cos \theta }\right)}^{f+1}{\left(\frac{1+\sin \theta }{1+\sin {\theta }_0}\right)}^f\end{array}}$

Se ha utilizado el resultado de la integral de la inversa del coseno

Tiempo de vuelo

ds=v·dt
ρdθ= v·dt

${\displaystyle \begin{array}{l}dt=-\frac{v}{g\sin \alpha \cos \theta }d\theta =\\ t=-\frac{v_0}{g\sin \alpha }\frac{{\left(\cos {\theta }_0\right)}^{f+1}}{{\left(1+\sin {\theta }_0\right)}^f}{\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}{\left(\frac{1+\sin \theta }{\cos \theta }\right)}^f\frac{d\theta }{{\cos }^2\theta }}\end{array}}$

Haciendo los cambios de variable

${\displaystyle \begin{array}{l}u=\tan \theta du=\frac{d\theta }{{\cos }^2\theta }\\ {{\displaystyle \int \left(\sqrt{1+u^2}+u\right)}}^{f}du\\ u=\sinh z\\ {{\displaystyle \int \left(\cosh z+\sinh z\right)}}^f\cosh z·dz=\frac{1}{2}{\displaystyle \int \left(e^{(f+1)z}+e^{(f-1)z}\right)}dz=\frac{e^{fz}}{2}\left(\frac{e^z}{f+1}+\frac{e^{-z}}{f-1}\right)\\ e^z=\frac{1+\sin \theta }{\cos \theta }{e}^{-z}=\frac{1-\sin \theta }{\cos \theta }\end{array}}$

llegamos al siguiente resultado

${\displaystyle \begin{array}{l}t={-\frac{v_0}{g\sin \alpha }\frac{{\left(\cos {\theta }_0\right)}^{f+1}}{{\left(1+\sin {\theta }_0\right)}^f}\left\{\frac{{\left(1+\sin \theta \right)}^f}{{\left(\cos \theta \right)}^f}\frac{\left(f-\sin \theta \right)}{\left(f^2-1\right)\cos \theta }\right\}|}_{{\theta }_0}^{\theta }=\\ \frac{1}{f^2-1}\frac{v_0}{g\sin \alpha }\left\{\left(f-\sin {\theta }_0\right)-{\left(\frac{\cos {\theta }_0}{\cos \theta }\right)}^{f+1}{\left(\frac{1+\sin \theta }{1+\sin {\theta }_0}\right)}^f\left(f-\sin \theta \right)\right\}\end{array}}$

Abscisa x

dx=ds·cosθ=ρdθ·cosθ

${\displaystyle \begin{array}{l}dx=-\frac{v^2}{g\sin \alpha \cos \theta }\cos \theta ·d\theta =-\frac{v^2}{g\sin \alpha }d\theta \hfill \\ x=-\frac{v_0^2}{g\sin \alpha }\frac{{\left(\cos {\theta }_0\right)}^{2f+2}}{{\left(1+\sin {\theta }_0\right)}^{2f}}\underset{{\theta }_0}{\overset{\theta }{{\displaystyle \int }}}{\left(\frac{1+\sin \theta }{\cos \theta }\right)}^{2f}\frac{d\theta }{{\cos }^2\theta }\hfill \end{array}}$

Haciendo los cambios de variable

${\displaystyle \begin{array}{l}u=\tan \theta du=\frac{d\theta }{{\cos }^2\theta }\\ {{\displaystyle \int \left(\sqrt{1+u^2}+u\right)}}^{2f}du\\ u=\sinh z\\ {{\displaystyle \int \left(\cosh z+\sinh z\right)}}^{2f}\cosh z·dz=\frac{1}{2}{\displaystyle \int \left(e^{(2f+1)z}+e^{(2f-1)z}\right)}dt=\frac{e^{2fz}}{2}\left(\frac{e^z}{2f+1}+\frac{e^{-z}}{2f-1}\right)\\ e^z=\frac{1+\sin \theta }{\cos \theta }{e}^{-z}=\frac{1-\sin \theta }{\cos \theta }\end{array}}$

Llegamos al siguiente resultado

${\displaystyle \begin{array}{l}x={-\frac{v_0^2}{g\sin \alpha }\frac{{\left(\cos {\theta }_0\right)}^{2f+2}}{{\left(1+\sin {\theta }_0\right)}^{2f}}\left\{\frac{{\left(1+\sin \theta \right)}^{2f}}{{\left(\cos \theta \right)}^{2f}}\frac{\left(2f-\sin \theta \right)}{\left(4f^2-1\right)\cos \theta }\right\}|}_{{\theta }_0}^{\theta }=\\ \frac{1}{4f^2-1}\frac{v_0^2}{g\sin \alpha }\left\{\left(2f-\sin {\theta }_0\right)\cos {\theta }_0-{\left(\frac{\cos {\theta }_0}{\cos \theta }\right)}^{2f+2}{\left(\frac{1+\sin \theta }{1+\sin {\theta }_0}\right)}^{2f}\cos \theta \left(2f-\sin \theta \right)\right\}\end{array}}$

Ordenada y

dy=ds·sinθ=ρdθ·sinθ

${\displaystyle \begin{array}{l}dy=-\frac{v^2}{g\sin \alpha \cos \theta }\sin \theta ·d\theta =-\frac{v^2}{g\sin \alpha }\tan \theta d\theta \hfill \\ y=-\frac{v_0^2}{g\sin \alpha }\frac{{\left(\cos {\theta }_0\right)}^{2f+2}}{{\left(1+\sin {\theta }_0\right)}^{2f}}\underset{{\theta }_0}{\overset{\theta }{{\displaystyle \int }}}{\left(\frac{1+\sin \theta }{\cos \theta }\right)}^{2f}\frac{\tan \theta }{{\cos }^2\theta }d\theta \hfill \end{array}}$

Haciendo los cambios de variable

${\displaystyle \begin{array}{l}u=\tan \theta du=\frac{d\theta }{{\cos }^2\theta }\\ {{\displaystyle \int \left(\sqrt{1+u^2}+u\right)}}^{2f}u·du\\ u=\sinh z\\ {{\displaystyle \int \left(\cosh z+\sinh z\right)}}^{2f}\sinh z·\cosh z·dz=\frac{1}{4}{\displaystyle \int \left(e^{(2f+2)z}-e^{(2f-2)z}\right)}dt=\frac{e^{2fz}}{8}\left(\frac{e^{2z}}{f+1}-\frac{e^{-2z}}{f-1}\right)\\ e^z=\frac{1+\sin \theta }{\cos \theta }{e}^{-z}=\frac{1-\sin \theta }{\cos \theta }\end{array}}$

llegamos al siguiente resultado

${\displaystyle \begin{array}{l}y={\frac{v_0^2}{g\sin \alpha }\frac{{\left(\cos {\theta }_0\right)}^{2f+2}}{{\left(1+\sin {\theta }_0\right)}^{2f}}\left\{{\left(\frac{1+\sin \theta }{\cos \theta }\right)}^{2f}\frac{\left(2f\sin \theta -1-{\sin }^2\theta \right)}{4\left(f^2-1\right){\cos }^2\theta }\right\}|}_{{\theta }_0}^{\theta }=\\ \frac{1}{4\left(f^2-1\right)}\frac{v_0^2}{g\sin \alpha }\left\{\left(2f\sin {\theta }_0-1-{\sin }^2{\theta }_0\right)-{\left(\frac{\cos {\theta }_0}{\cos \theta }\right)}^{2f+2}{\left(\frac{1+\sin \theta }{1+\sin {\theta }_0}\right)}^{2f}\left(2f\sin \theta -1-{\sin }^2\theta \right)\right\}\end{array}}$

Trayectorias cuando el proyectil se detiene, f>1

Cuando f>1 el proyectil se detiene v=0, la dirección de la velocidad hace un ángulo θ=-π/2.

En la expresión de la velocidad v en función del ángulo θ

${\displaystyle v=v_0{\left(\frac{\cos {\theta }_0}{\cos \theta }\right)}^{f+1}{\left(\frac{1+\sin \theta }{1+\sin {\theta }_0}\right)}^f}$

obtenemos un cociente 0/0 cuando θ=-π/2. Resolvemos esta indeterminación, del siguiente modo

${\displaystyle \begin{array}{l}\frac{{\left(1+\sin \theta \right)}^f}{{\left(\cos \theta \right)}^{f+1}}=\frac{{\left({\left(\cos \frac{\theta }{2}+\sin \frac{\theta }{2}\right)}^2\right)}^f}{{\left(\left(\cos \frac{\theta }{2}+\sin \frac{\theta }{2}\right)\left(\cos \frac{\theta }{2}-\sin \frac{\theta }{2}\right)\right)}^{f+1}}=\frac{{\left(\cos \frac{\theta }{2}+\sin \frac{\theta }{2}\right)}^{f-1}}{{\left(\cos \frac{\theta }{2}-\sin \frac{\theta }{2}\right)}^{f+1}}\\ \underset{\theta \to -\frac{\pi }{2}}{\lim }\frac{{\left(1+\sin \theta \right)}^f}{{\left(\cos \theta \right)}^{f+1}}=\underset{\theta \to -\frac{\pi }{2}}{\lim }\frac{{\left(\cos \frac{\theta }{2}+\sin \frac{\theta }{2}\right)}^{f-1}}{{\left(\cos \frac{\theta }{2}-\sin \frac{\theta }{2}\right)}^{f+1}}=0f>1\end{array}}$

Otro resultado notable, el límite tiende a 1/2 cuando f=1

Teniendo en cuenta este resultado para f>1, el instante t₁ en el que el proyectil se detiene es

${\displaystyle t_1=\frac{1}{f^2-1}\frac{v_0}{g\sin \alpha }\left(f-\sin {\theta }_0\right)}$

Su posición (x₁, y₁) es

${\displaystyle \begin{array}{l}{x}_1=\frac{1}{4f^2-1}\frac{v_0^2}{g\sin \alpha }\left(2f-\sin {\theta }_0\right)\cos {\theta }_0\\ y_1=\frac{1}{4\left(f^2-1\right)}\frac{v_0^2}{g\sin \alpha }\left(2f\sin {\theta }_0-1-{\sin }^2{\theta }_0\right)\end{array}}$

Representamos la velocidad del proyectil en función del tiempo hasta que se detiene. El ángulo de disparo es θ₀=-30°, el ángulo del plano inclinado es α=30°, la velocidad de disparo es v₀=1, y el parámetro que mide el rozamiento f=2

f=2;
alfa=pi/6;
ang=-pi/6;
v0=1;
v=@(th) v0*((cos(ang)./cos(th)).^(f+1)).*((1+sin(th))/(1+sin(ang))).^f;
t=@(th) v0*((f-sin(ang))-((cos(ang)./cos(th)).^(f+1)).*
(((1+sin(th))/(1+sin(ang))).^f).*(f-sin(th)))/((f^2-1)*9.8*sin(alfa));
fplot(t,v,[-pi/2,ang])
grid on
xlabel('t')
ylabel('v')
title('velocidad')

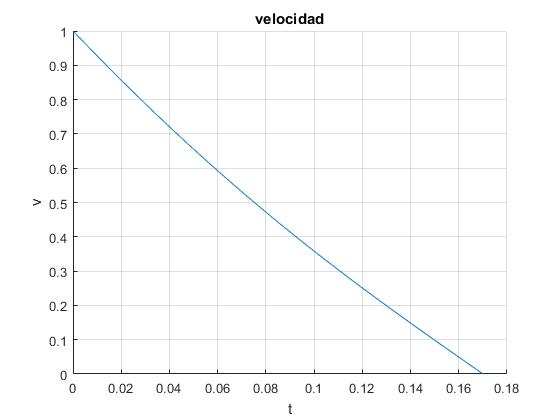
Calculamos el tiempo t₁ que tarda en detenerse

>> t1 = v0*(f - sin(ang))/((f^2 - 1)*9.8*sin(alfa))
t1 =    0.1701

Casos particulares

• Para θ₀=π/2

${\displaystyle \begin{array}{l}{x}_1=0\\ y_1=\frac{1}{4(f^2-1)}\frac{v_0^2}{g\sin \alpha }\left(2f-2\right)=\frac{1}{2}\frac{v_0^2}{g\sin \alpha }\frac{1}{\frac{\mu }{\tan \alpha }+1}=\frac{1}{2}\frac{v_0^2}{g\left(\sin \alpha +\mu \cos \alpha \right)}\end{array}}$

• Para θ₀=-π/2

${\displaystyle \begin{array}{l}{x}_1=0\\ y_1=\frac{1}{4(f^2-1)}\frac{v_0^2}{g\sin \alpha }\left(-2f-2\right)=-\frac{1}{2}\frac{v_0^2}{g\sin \alpha }\frac{1}{\frac{\mu }{\tan \alpha }-1}=-\frac{1}{2}\frac{v_0^2}{g\left(-\sin \alpha +\mu \cos \alpha \right)}\end{array}}$

Resultados que hemos obtenido al principio de esta página

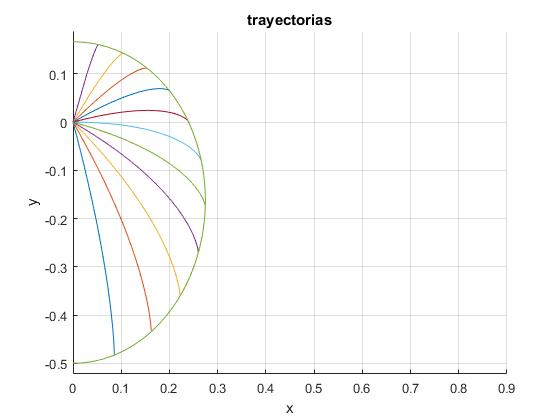
Dibujamos la curva que une los puntos (x₁, y₁) para todos los ángulos de tiro -π/2≤θ₀≤π/2 para un determinado valor de f>1. Se ha fijado la velocidad de disparo $v_0^2=g\sin \alpha$

hold on
for f=[2,3,4,6,10]
    x1=@(th) (2*f-sin(th)).*cos(th)/(4*f^2-1);
    y1=@(th) (2*f*sin(th)-1-sin(th).^2)/(4*(f^2-1));
    fplot(x1,y1,[-pi/2,pi/2], 'displayName',num2str(f));
end
axis equal
hold off
grid on
legend('-DynamicLegend','location','northeast')
xlabel('x')
ylabel('y')
title('Envolventes')

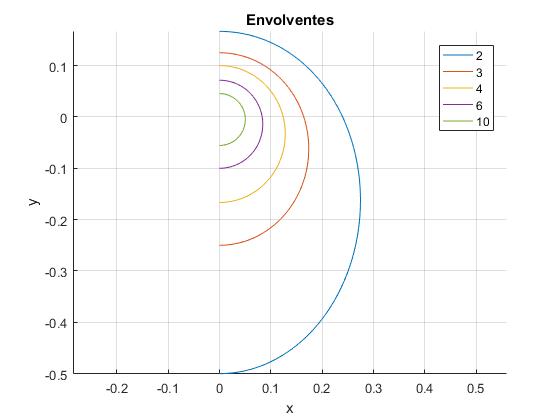
El proyectil recorre más distancia cuando el ángulo de tiro apunta hacia abajo θ₀=-π/2 que cuando apunta hacia arriba θ₀=π/2. A medida que se incrementa el rozamiento f, las distancias hasta que se detiene el proyectil se hacen cada vez más pequeñas

Cuando f se hace grande, (x₁, y₁) tienden a

${\displaystyle \begin{array}{l}{x}_1=\frac{1}{4f^2}\frac{v_0^2}{g\sin \alpha }2f\cos {\theta }_0=\frac{1}{2f}\frac{v_0^2}{g\sin \alpha }\cos {\theta }_0\\ y_1=\frac{1}{4f^2}\frac{v_0^2}{g\sin \alpha }2f\sin {\theta }_0=\frac{1}{2f}\frac{v_0^2}{g\sin \alpha }\sin {\theta }_0\\ x_1^2+y_1^2=\frac{1}{4f^2}\frac{v_0^4}{g^2{\sin }^2\alpha }\end{array}}$

Los puntos (x₁, y₁) están situados en una semicircunferencia de radio r (la más interior de color verde, con la etiqueta de f=10)

${\displaystyle r=\frac{1}{2f}\frac{v_0^2}{g\sin \alpha }}$

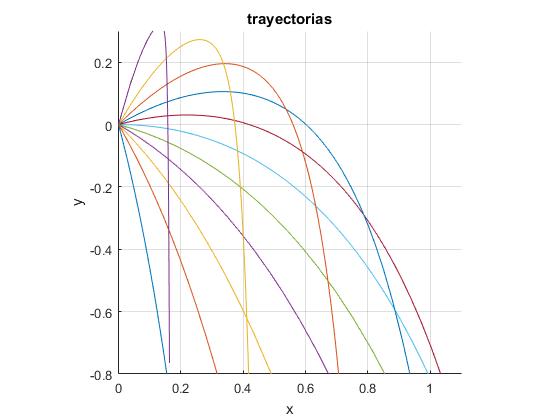
Dibujamos las trayectorias de los proyectiles lanzados con la misma velocidad de disparo v₀, con ángulos de tiro espaciados 15°=π/12. El valor del parámetro f=2. Se dibuja la curva que une los puntos (x₁, y₁) en los que se detiene el proyectil

f=2;
hold on
for ang=-pi/2+pi/12:pi/12:pi/2-pi/12
    x=@(th) ((2*f-sin(ang))*cos(ang)-((cos(ang)./cos(th)).^(2*f+2)).
*(((1+sin(th))/(1+sin(ang))).^(2*f)).*cos(th).*(2*f-sin(th)))/(4*f^2-1);
    y=@(th) ((2*f*sin(ang)-1-sin(ang)^2)-((cos(ang)./cos(th)).^(2*f+2)).
*(((1+sin(th))/(1+sin(ang))).^(2*f)).*(2*f*sin(th)-1-sin(th).^2))/(4*(f^2-1));
    fplot(x,y,[-pi/2,ang])
end
x1=@(th) (2*f-sin(th)).*cos(th)/(4*f^2-1);
y1=@(th) (2*f*sin(th)-1-sin(th).^2)/(4*(f^2-1));
fplot(x1,y1,[-pi/2,pi/2]);
axis equal
xlim([0,0.9])
grid on
hold off
xlabel('x')
ylabel('y')
title('trayectorias')

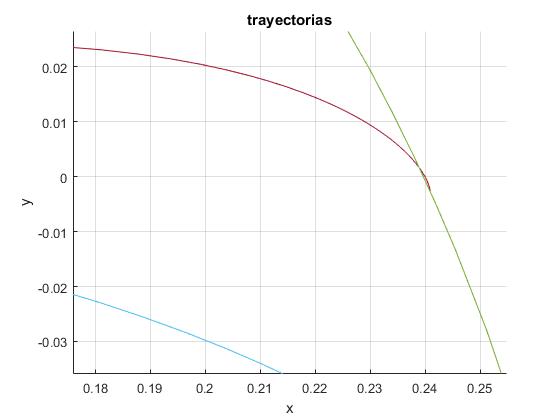
Utilizamos las herramientas Zoom in y Pan de la ventana gráfica, para observar el final de la trayectoria de un proyectil, cómo se curva hasta que la tangente a la trayectoria alcanza el ángulo límite θ=-π/2

Trayectorias cuando el proyectil no se detiene, f<1

Velocidad del proyectil

Representamos la velocidad del proyectil en función del tiempo, para un ángulo de tiro de θ=45°, la velocidad de disparo es v₀=1, el ángulo del plano inclinado α=30°, el parámetro f=0.7

f=0.7;
alfa=pi/6;
ang=pi/4;
v=@(th) ((cos(ang)./cos(th)).^(f+1)).*((1+sin(th))/(1+sin(ang))).^f;
t=@(th) ((f-sin(ang))-((cos(ang)./cos(th)).^(f+1)).*
(((1+sin(th))/(1+sin(ang))).^f).*(f-sin(th)))/((f^2-1)*9.8*sin(alfa));
fplot(t,v,[-pi/2+0.001,ang])
grid on
xlabel('t')
ylabel('v')
title('velocidad')

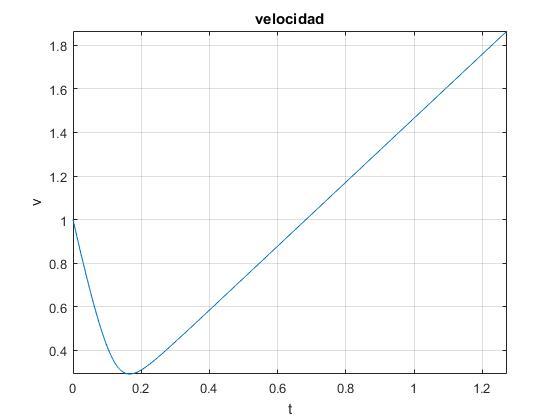
Vemos que el módulo de la velocidad disminuye, hasta que alcanza la altura máxima y luego vuelve a aumentar

Trayectorias de los proyectiles

Examinamos las trayectorias de los proyectiles disparados desde el origen con ángulos espaciados 15°, para f=0.7

f=0.7;
hold on
for ang=-pi/2+pi/12:pi/12:pi/2-pi/12
    x=@(th) ((2*f-sin(ang))*cos(ang)-((cos(ang)./cos(th)).^(2*f+2)).
*(((1+sin(th))/(1+sin(ang))).^(2*f)).*cos(th).*(2*f-sin(th)))/(4*f^2-1);
    y=@(th) ((2*f*sin(ang)-1-sin(ang)^2)-((cos(ang)./cos(th)).^(2*f+2)).
*(((1+sin(th))/(1+sin(ang))).^(2*f)).*(2*f*sin(th)-1-sin(th).^2))/(4*(f^2-1));
    fplot(x,y,[-pi/2+0.0001,ang])
end
axis equal
ylim([-0.8,0.3])
xlim([0,0.9])
grid on
hold off
xlabel('x')
ylabel('y')
title('trayectorias')

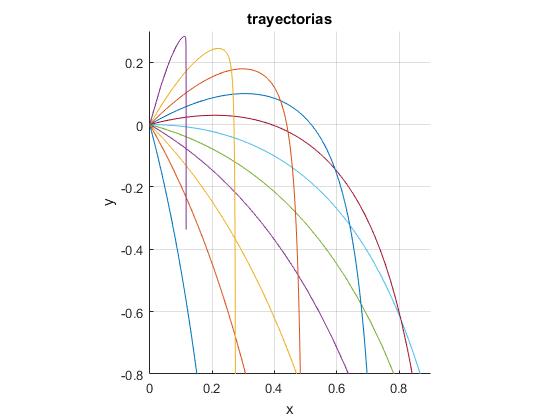
Observamos que los proyectiles disparados con un ángulo próximo a 90° se curvan rápidamente y descienden siguiendo una trayectoria que es casi una línea recta paralela al eje Y. Observamos que el alcance de los proyectiles está limitado

Cuando θ tiende a -π/2, la ordenada y tiende a infinito. Sin embargo, la abscisa x tiene un comportamiento diferente

${\displaystyle \begin{array}{l}\frac{{\left(1+\sin \theta \right)}^{2f}}{{\left(\cos \theta \right)}^{2f+1}}=\frac{{\left(\cos \frac{\theta }{2}+\sin \frac{\theta }{2}\right)}^{2f}}{{\left(\left(\cos \frac{\theta }{2}+\sin \frac{\theta }{2}\right)\left(\cos \frac{\theta }{2}-\sin \frac{\theta }{2}\right)\right)}^{2f+1}}=\frac{{\left(\cos \frac{\theta }{2}+\sin \frac{\theta }{2}\right)}^{2f-1}}{{\left(\cos \frac{\theta }{2}-\sin \frac{\theta }{2}\right)}^{2f+1}}\\ \underset{\theta \to -\frac{\pi }{2}}{\lim }\frac{{\left(1+\sin \theta \right)}^{2f}}{{\left(\cos \theta \right)}^{2f+1}}=\underset{\theta \to -\frac{\pi }{2}}{\lim }\frac{{\left(\cos \frac{\theta }{2}+\sin \frac{\theta }{2}\right)}^{2f-1}}{{\left(\cos \frac{\theta }{2}-\sin \frac{\theta }{2}\right)}^{2f+1}}=00.5<f\le 1\end{array}}$

Otro resultado notable, el límite tiende a 1/2 cuando f=0.5

Llevando este resultado a la expresión de x (aquí abajo) obtenemos x_∞

${\displaystyle \begin{array}{l}x=\frac{1}{4f^2-1}\frac{v_0^2}{g\sin \alpha }\left\{\left(2f-\sin {\theta }_0\right)\cos {\theta }_0-{\left(\frac{\cos {\theta }_0}{\cos \theta }\right)}^{2f+2}{\left(\frac{1+\sin \theta }{1+\sin {\theta }_0}\right)}^{2f}\cos \theta \left(2f-\sin \theta \right)\right\}\\ x_{\infty }=\frac{1}{4f^2-1}\frac{v_0^2}{g\sin \alpha }\left(2f-\sin {\theta }_0\right)\cos {\theta }_0\end{array}}$

Representamos la trayectoria de un proyectil disparado con ángulo de tiro θ₀=π/4, y dibujamos mediante una línea a trazos su asíntota vertical x_∞

f=0.7;
ang=pi/4;
x=@(th) ((2*f-sin(ang))*cos(ang)-((cos(ang)./cos(th)).^(2*f+2)).
*(((1+sin(th))/(1+sin(ang))).^(2*f)).*cos(th).*(2*f-sin(th)))/(4*f^2-1);
y=@(th) ((2*f*sin(ang)-1-sin(ang)^2)-((cos(ang)./cos(th)).^(2*f+2)).
*(((1+sin(th))/(1+sin(ang))).^(2*f)).*(2*f*sin(th)-1-sin(th).^2))/(4*(f^2-1));
fplot(x,y,[-pi/2+0.0001,ang])
x_inf=(2*f-sin(ang))*cos(ang)/(4*f^2-1);
line([x_inf,x_inf],[-0.8,0.4],'linestyle','--','color','k')
axis equal
ylim([-0.8,0.4])
xlim([0,1.3])
grid on
xlabel('x')
ylabel('y')
title('trayectorias')

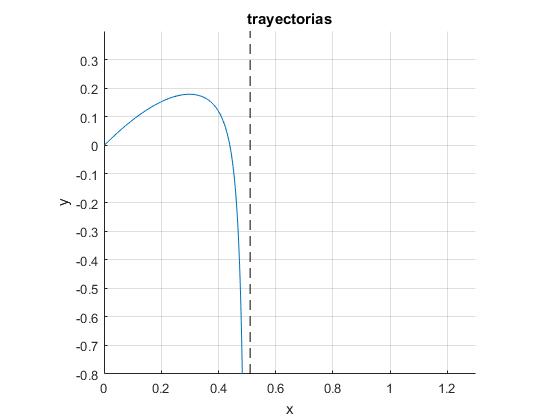
La altura máxima de un proyectil disparado con ángulo de tiro, θ₀>0, se obtiene para θ=0

>> y(0)
ans =    0.1787

Cambiamos el parámetro f=0.3, y volvemos a dibujar las trayectorias

f=0.3;
hold on
for ang=-pi/2+pi/12:pi/12:pi/2-pi/12
    x=@(th) ((2*f-sin(ang))*cos(ang)-((cos(ang)./cos(th)).^(2*f+2)).
*(((1+sin(th))/(1+sin(ang))).^(2*f)).*cos(th).*(2*f-sin(th)))/(4*f^2-1);
    y=@(th) ((2*f*sin(ang)-1-sin(ang)^2)-((cos(ang)./cos(th)).^(2*f+2)).
*(((1+sin(th))/(1+sin(ang))).^(2*f)).*(2*f*sin(th)-1-sin(th).^2))/(4*(f^2-1));
    fplot(x,y,[-pi/2+0.0001,ang])
end
axis equal
ylim([-0.8,0.4])
xlim([0,1.3])
grid on
hold off
xlabel('x')
ylabel('y')
title('trayectorias')

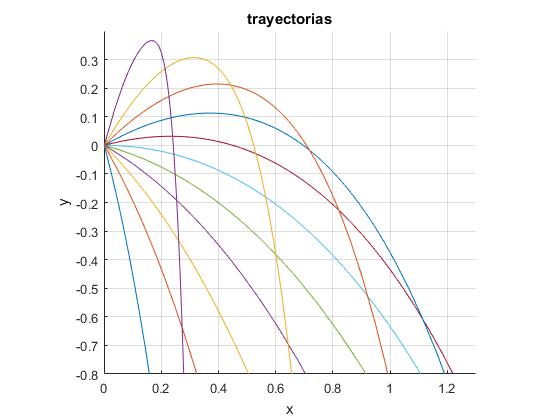
Casos especiales f=1 y f=0.5

Examinamos primeros el caso f=1, la velocidad del proyectil es

${\displaystyle v=v_0{\left(\frac{\cos {\theta }_0}{\cos \theta }\right)}^2\left(\frac{1+\sin \theta }{1+\sin {\theta }_0}\right)}$

Hemos demostrado que el límite cuando θ tiende a -π/2

${\displaystyle \underset{\theta \to -\frac{\pi }{2}}{\lim }\frac{\left(1+\sin \theta \right)}{{\left(\cos \theta \right)}^2}=\underset{\theta \to -\frac{\pi }{2}}{\lim }\frac{1}{{\left(\cos \frac{\theta }{2}-\sin \frac{\theta }{2}\right)}^2}=\frac{1}{2}}$

La velocidad tiende al valor constante

${\displaystyle v_{\infty }=\frac{v_0}{2}\frac{{\cos }^2{\theta }_0}{1+\sin {\theta }_0}}$

Para f=1, tenemos que volver a calcular la expresión del tiempo t y la expresión de la ordenada y, debido a que en el denominador contienen el término (f²-1) que se hace cero

Tiempo t

${\displaystyle \begin{array}{l}dt=-\frac{v}{g\sin \alpha \cos \theta }d\theta =\\ t=-\frac{v_0}{g\sin \alpha }\frac{{\left(\cos {\theta }_0\right)}^2}{\left(1+\sin {\theta }_0\right)}{\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}\left(\frac{1+\sin \theta }{\cos \theta }\right)\frac{d\theta }{{\cos }^2\theta }}\end{array}}$

Haciendo los cambios de variable

${\displaystyle \begin{array}{l}u=\tan \theta du=\frac{d\theta }{{\cos }^2\theta }\\ {\displaystyle \int \left(\sqrt{1+u^2}+u\right)}du\\ u=\sinh z\\ {\displaystyle \int \left(\cosh z+\sinh z\right)}\cosh z·dz=\frac{1}{2}{\displaystyle \int \left(e^{2z}+1\right)}dz=\frac{1}{2}\left(\frac{e^{2z}}{2}+z\right)\\ e^z=\frac{1+\sin \theta }{\cos \theta }\end{array}}$

llegamos al siguiente resultado

${\displaystyle \begin{array}{l}t={-\frac{v_0}{g\sin \alpha }\frac{{\left(\cos {\theta }_0\right)}^2}{\left(1+\sin {\theta }_0\right)}\frac{1}{2}\left\{\frac{1}{2}\frac{{\left(1+\sin \theta \right)}^2}{{\left(\cos \theta \right)}^2}+\ln \left|\frac{1+\sin \theta }{\cos \theta }\right|\right\}|}_{{\theta }_0}^{\theta }=\\ \frac{1}{2}\frac{v_0}{g\sin \alpha }\frac{{\left(\cos {\theta }_0\right)}^2}{\left(1+\sin {\theta }_0\right)}\left\{\frac{1}{2}\frac{{\left(1+\sin {\theta }_0\right)}^2}{{\left(\cos {\theta }_0\right)}^2}+\ln \left|\frac{1+\sin {\theta }_0}{\cos {\theta }_0}\right|-\frac{1}{2}\frac{{\left(1+\sin \theta \right)}^2}{{\left(\cos \theta \right)}^2}-\ln \left|\frac{1+\sin \theta }{\cos \theta }\right|\right\}\end{array}}$

Representamos la velocidad del proyectil en función del tiempo, para un ángulo de tiro θ₀=30°, la velocidad de disparo es v₀=1, el ángulo del plano inclinado α=30°, el parámetro f=1

f=1;
alfa=pi/6;
ang=pi/6;
v=@(th) ((cos(ang)./cos(th)).^(f+1)).*((1+sin(th))/(1+sin(ang))).^f;
t=@(th) cos(ang)^2*(((1+sin(ang))/cos(ang))^2/2+log((1+sin(ang))/cos(ang))
-((1+sin(th))./cos(th)).^2/2-log((1+sin(th))./cos(th)))
/(2*9.8*sin(alfa)*(1+sin(ang)));
fplot(t,v,[-pi/2+0.001,ang])
grid on
ylim([0,1])
xlabel('t')
ylabel('v')
title('velocidad')

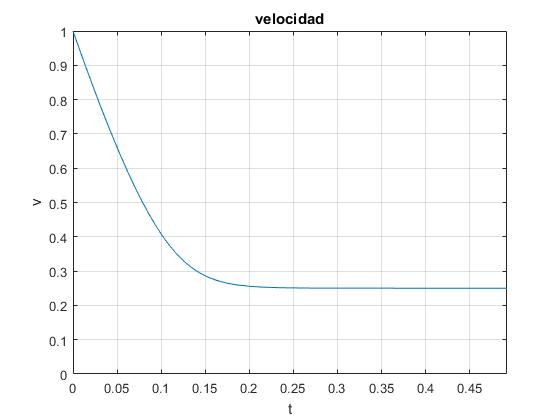
Observamos que la velocidad tiende hacia un valor límite constante

0.5*cos(ang)^2/(1+sin(ang))
ans =    0.2500

Ordenada y

${\displaystyle \begin{array}{l}dy=-\frac{v^2}{g\sin \alpha \cos \theta }\sin \theta ·d\theta =-\frac{v^2}{g\sin \alpha }\tan \theta d\theta \hfill \\ y=-\frac{v_0^2}{g\sin \alpha }\frac{{\left(\cos {\theta }_0\right)}^4}{{\left(1+\sin {\theta }_0\right)}^2}\underset{{\theta }_0}{\overset{\theta }{{\displaystyle \int }}}{\left(\frac{1+\sin \theta }{\cos \theta }\right)}^2\frac{\tan \theta }{{\cos }^2\theta }d\theta \hfill \end{array}}$

Haciendo los cambios de variable

${\displaystyle \begin{array}{l}u=\tan \theta du=\frac{d\theta }{{\cos }^2\theta }\\ {{\displaystyle \int \left(\sqrt{1+u^2}+u\right)}}^{2}u·du\\ u=\sinh z\\ {{\displaystyle \int \left(\cosh z+\sinh z\right)}}^2\sinh z·\cosh z·dz=\frac{1}{4}{\displaystyle \int \left(e^{4z}-1\right)}dt=\frac{1}{4}\left(\frac{e^{4z}}{4}-z\right)\\ e^z=\frac{1+\sin \theta }{\cos \theta }\end{array}}$

Llegamos al siguiente resultado

${\displaystyle \begin{array}{l}y={\frac{1}{4}\frac{v_0^2}{g\sin \alpha }\frac{{\left(\cos {\theta }_0\right)}^4}{{\left(1+\sin {\theta }_0\right)}^2}\left\{\frac{1}{4}{\left(\frac{1+\sin \theta }{\cos \theta }\right)}^4-\ln \left|\frac{1+\sin \theta }{\cos \theta }\right|\right\}|}_{{\theta }_0}^{\theta }=\\ \frac{1}{4}\frac{v_0^2}{g\sin \alpha }\frac{{\left(\cos {\theta }_0\right)}^4}{{\left(1+\sin {\theta }_0\right)}^2}\left\{\frac{1}{4}{\left(\frac{1+\sin {\theta }_0}{\cos {\theta }_0}\right)}^4-\ln \left|\frac{1+\sin {\theta }_0}{\cos {\theta }_0}\right|-\frac{1}{4}{\left(\frac{1+\sin \theta }{\cos \theta }\right)}^4+\ln \left|\frac{1+\sin \theta }{\cos \theta }\right|\right\}\end{array}}$

La expresión de la abscisa x sigue siendo la misma que hemos deducido para los otros casos

${\displaystyle x=\frac{1}{4f^2-1}\frac{v_0^2}{g\sin \alpha }\left\{\left(2f-\sin {\theta }_0\right)\cos {\theta }_0-{\left(\frac{\cos {\theta }_0}{\cos \theta }\right)}^{2f+2}{\left(\frac{1+\sin \theta }{1+\sin {\theta }_0}\right)}^{2f}\cos \theta \left(2f-\sin \theta \right)\right\}}$

Dibujamos las trayectorias de los proyectiles lanzados con la misma velocidad de disparo v₀, con ángulos de tiro espaciados 15°=π/12. El valor del parámetro f=1.

f=1;
hold on
for ang=-pi/2+pi/12:pi/12:pi/2-pi/12
    x=@(th) ((2*f-sin(ang))*cos(ang)-((cos(ang)./cos(th)).^(2*f+2)).
*(((1+sin(th))/(1+sin(ang))).^(2*f)).*cos(th).*(2*f-sin(th)))/(4*f^2-1);
    y=@(th) cos(ang)^4*(((1+sin(ang))/cos(ang))^4/4-log((1+sin(ang))/cos(ang))-
((1+sin(th))./cos(th)).^4/4+log((1+sin(th))./cos(th)))/(4*(1+sin(ang))^2);
    fplot(x,y,[-pi/2,ang])
end
axis equal
ylim([-0.8,0.3])
xlim([0,0.7])
grid on
hold off
xlabel('x')
ylabel('y')
title('trayectorias')

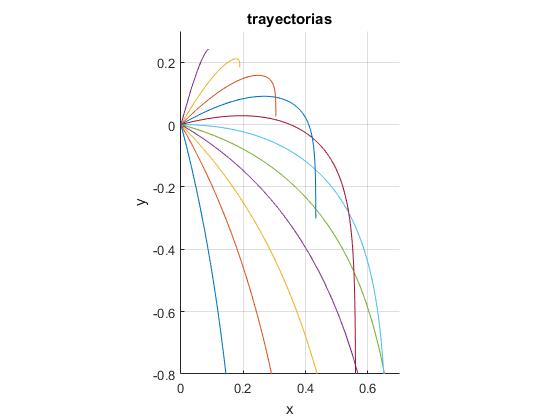
La abscisa x está limitada cuando θ tiende a -π/2, situación que ya observamos para 0.5<f≤1

f=0.5

Examinamos ahora el caso f=0.5. El denominador de la abscisa x contiene el término (4f²-1), que se hace cero cuando f=0.5. Es preciso volver a calcular la abscisa x

${\displaystyle \begin{array}{l}dx=-\frac{v^2}{g\sin \alpha \cos \theta }\cos \theta ·d\theta =-\frac{v^2}{g\sin \alpha }d\theta \hfill \\ x=-\frac{v_0^2}{g\sin \alpha }\frac{{\left(\cos {\theta }_0\right)}^3}{\left(1+\sin {\theta }_0\right)}\underset{{\theta }_0}{\overset{\theta }{{\displaystyle \int }}}\left(\frac{1+\sin \theta }{\cos \theta }\right)\frac{d\theta }{{\cos }^2\theta }\hfill \end{array}}$

Haciendo los cambios de variable

${\displaystyle \begin{array}{l}u=\tan \theta du=\frac{d\theta }{{\cos }^2\theta }\\ {\displaystyle \int \left(\sqrt{1+u^2}+u\right)}du\\ u=\sinh z\\ {\displaystyle \int \left(\cosh z+\sinh z\right)}\cosh z·dz=\frac{1}{2}{\displaystyle \int \left(e^{2z}+1\right)}dt=\frac{1}{2}\left(\frac{e^{2z}}{2}+z\right)\\ e^z=\frac{1+\sin \theta }{\cos \theta }\end{array}}$

Llegamos al resultado

${\displaystyle \begin{array}{l}x={-\frac{v_0^2}{g\sin \alpha }\frac{{\cos }^3{\theta }_0}{\left(1+\sin {\theta }_0\right)}\frac{1}{2}\left\{\frac{1}{2}{\left(\frac{1+\sin \theta }{\cos \theta }\right)}^2+\ln \left|\frac{1+\sin \theta }{\cos \theta }\right|\right\}|}_{{\theta }_0}^{\theta }=\\ \frac{1}{2}\frac{v_0^2}{g\sin \alpha }\frac{{\cos }^3{\theta }_0}{\left(1+\sin {\theta }_0\right)}\left\{\frac{1}{2}{\left(\frac{1+\sin {\theta }_0}{\cos {\theta }_0}\right)}^2+\ln \left|\frac{1+\sin {\theta }_0}{\cos {\theta }_0}\right|-\frac{1}{2}{\left(\frac{1+\sin \theta }{\cos \theta }\right)}^2-\ln \left|\frac{1+\sin \theta }{\cos \theta }\right|\right\}\end{array}}$

Las expresiones de la ordenada y y del tiempo t no han cambiado

Dibujamos las trayectorias de los proyectiles lanzados con la misma velocidad de disparo v₀, con ángulos de tiro espaciados 15°=π/12. El valor del parámetro f=0.5.

f=0.5;
hold on
for ang=-pi/2+pi/12:pi/12:pi/2-pi/12
     x=@(th) cos(ang)^3*(((1+sin(ang))/cos(ang))^2/2+log((1+sin(ang))/cos(ang))-
((1+sin(th))./cos(th)).^2/2-log((1+sin(th))./cos(th)))/(2*(1+sin(ang)));
    y=@(th) ((2*f*sin(ang)-1-sin(ang)^2)-((cos(ang)./cos(th)).^(2*f+2)).
*(((1+sin(th))/(1+sin(ang))).^(2*f)).*(2*f*sin(th)-1-sin(th).^2))/(4*(f^2-1));
    fplot(x,y,[-pi/2,ang])
end
axis equal
ylim([-0.8,0.3])
xlim([0,1.1])
grid on
hold off
xlabel('x')
ylabel('y')
title('trayectorias')

Referencias

Xiaosun Wang. Trajectory of a projectile on a frictional inclined plane. Am. J. Phys. 82 (8) August 2014, pp. 764-768