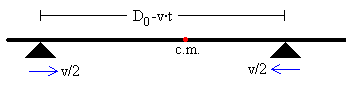
Sea D₀ la separación inicial entre los dos apoyos, si cada apoyo se mueve con velocidad constante v/2 uno hacia el otro, al cabo de un cierto tiempo t, la separación entre los mismos será D=D₀-v·t.

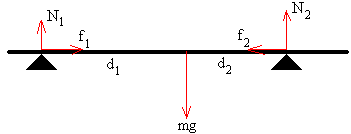
Consideremos la situación en la que el apoyo de la izquierda dista d₁ del centro de masas (c.m.) y el apoyo de la derecha dista d₂=D-d₁ del c. m. Dibujamos las fuerzas sobre la barra y aplicamos las condiciones de equilibrio

1. La resultante de las fuerzas ha de ser cero

N₁+N₂=mg

donde N₁ es la fuerza que ejerce el apoyo izquierdo y N₂ es la fuerza que ejerce el apoyo derecho sobre la barra.

2. El momento total respecto del cualquier punto debe ser cero. Si elegimos el apoyo derecho, como origen.

-N₁·(d₁+d₂)+mg·d₂=0

Despejamos N₁ y N₂ en este sistema de dos ecuaciones

${\displaystyle N_1=mg\frac{d_2}{d_1+d_2}{N}_2=mg\frac{d_1}{d_1+d_2}}$

• Al moverse el primer apoyo hacia la derecha, ejerce una fuerza de rozamiento f₁ sobre la barra dirigida hacia la derecha.

• Al moverse el segundo apoyo hacia la izquierda, ejerce una fuerza de rozamiento f₂ sobre la barra dirigida hacia la izquierda.

Ambas fuerzas son iguales f₁=f₂

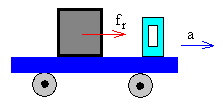
Para entender mejor el sentido de estas dos fuerzas, nos fijaremos que cuando un camión, que trasporta una caja de masa m sobre la plataforma, arranca, la fuerza de rozamiento f_r=ma entre la caja y la plataforma hace que la caja permanezca en reposo sobre la plataforma, siempre que se cumpla que f_r< μ_s·N.

Cuando la aceleración a del camión es tal que  f_r alcanza el valor máximo μ_s·N, la caja empieza a deslizar sobre la plataforma. La fuerza de rozamiento vale ahora f_r= μ_k·N.

Examinamos los distintos casos del movimiento de la barra con relación a los apoyos:

1. El apoyo izquierdo desliza, el apoyo derecho permanece en reposo relativo a la barra.

La fuerza de rozamiento entre la barra y los apoyos vale.

f₁=μ_k·N₁
f₁=f₂< μ_s·N₂

Como la distancia d₁ del apoyo izquierdo al c.m. disminuye, permaneciendo invariable la distancia d₂ del apoyo derecho al c.m., N₁ va aumentando hasta que se alcanza el valor máximo de la fuerza de rozamiento f₂=μ_s·N₂. El apoyo derecho empezará en este instante, a deslizar

Calculamos la distancia D₁=d₁+d₂ entre los dos apoyos en el momento en el que se cumple que

μ_k·N₁= μ_s·N₂, o bien,
μ_k·d₂= μ_s·d₁.

${\displaystyle D_1=\left(1+\frac{{\mu }_s}{{\mu }_k}\right)d_1}$

2. El apoyo derecho desliza, el apoyo izquierdo permanece en reposo relativo a la barra.

f₂=μ_k·N₂
f₂=f₁< μ_s·N₁

Como la distancia d₂ del apoyo derecho al c.m. disminuye, permaneciendo invariable la distancia d₁ del apoyo izquierdo al c.m., N₂ va aumentando hasta que se alcanza el valor máximo de la fuerza de rozamiento f₁=μ_s·N₁. El apoyo izquierdo empezará en este instante a deslizar

Calculamos la distancia D₂=d₁+d₂ entre los dos apoyos en el momento en el que se cumple que

μ_s·N₁= μ_k·N₂, o bien,
μ_s·d₂= μ_k·d₁.

${\displaystyle D_2=\left(1+\frac{{\mu }_k}{{\mu }_s}\right)d_1}$

El cociente entre ambas distancias es

${\displaystyle \frac{D_2}{D_1}=\frac{({\mu }_s+{\mu }_k)/{\mu }_s}{({\mu }_s+{\mu }_k)/{\mu }_k}=\frac{{\mu }_k}{{\mu }_s}}$

El proceso se repite indefinidamente, la relación entre dos distancias consecutivas D_n+1 y D_n será por tanto,

${\displaystyle \frac{D_{n+1}}{D_n}=\frac{{\mu }_k}{{\mu }_s}}$

Ejemplo

• Distancia del apoyo izquierdo al c.m., d₁=50 cm

• Distancia del apoyo derecho al c.m., d₂=45 cm

• Coeficiente estático, μ_s=1.0

• Coeficiente cinético, μ_k=0.8

• Peso de la barra mg=1.0 N

• La velocidad relativa de acercamiento de los apoyos, v=1.0 cm/s

1. Desliza el apoyo izquierdo, el apoyo derecho permanece en reposo relativo a la barra.

La distancia d₁ disminuye, d₁=50-1·t cm

La distancia d₂=45 cm permanece invariable

El valor de la fuerza de rozamiento es f₂=f₁=μ_k·N₁

Como d₁ disminuye, N₁  aumenta, hasta que f₂ alcanza su valor máximo f₂=μ_s·N₂, en ese instante el apoyo derecho comienza a deslizar.

μ_k·N₁=μ_s·N₂. o bien,  μ_k·d₂=μ_s·d₁

0.8·45=1.0·d₁,   d₁=36 cm

La distancia entre los dos apoyos es D₁=d₁+d₂=45+36=81 cm

El instante en el que se alcanza esta posición es 36=50-t, t=14 s

2. Desliza el apoyo derecho, el apoyo izquierdo permanece en reposo relativo a la barra.

La distancia d₂ disminuye, d₂=45-1·(t-14)  cm

La distancia d₁=36 cm permanece invariable

El valor de la fuerza de rozamiento es f₁=f₂=μ_k·N₂

Como d₂ disminuye, N₂ aumenta, hasta que f₁ alcanza su valor máximo f₁=μ_s·N₁, en ese instante el apoyo izquierdo comienza a deslizar.

μ_s·N₁=μ_k·N₂. o bien,  μ_s·d₂=μ_k·d₁

1.0·d₂=0.8·36,     d₂=28.8 cm

La distancia entre los dos apoyos es D₂=d₁+d₂=36+28.8=64.8 cm

El instante en el que se alcanza esta posición es 28.8=45-(t-14), t=30.2 s

El cociente entre las distancias D₂/D₁=64.8/81, es igual al cociente entre los coeficientes cinético μ_k=0.8 y estático μ_s=1.0.

3. Desliza el apoyo izquierdo, el apoyo derecho permanece en reposo relativo a la barra.

Su descripción es análoga a la primera etapa

4. Desliza el apoyo derecho, el apoyo izquierdo permanece en reposo relativo a la barra.

Su descripción es análoga a la segunda etapa

Actividades

Se pulsa el botón titulado Nuevo.

• Se establece la distancia inicial entre los apoyos, en el control titulado Posición

Se introduce

• El coeficiente cinético μ_k, actuando en la barra de desplazamiento titulada Coef. cinético.

Se pulsa el botón titulado Nuevo

El programa interactivo ha fijado los valores de:

• El coeficiente estático μ_s=1.0

• La longitud de la barra en 100 cm

• La velocidad relativa de acercamiento de los apoyos en v=1 cm/s. El apoyo se izquierdo se desplaza hacia la derecha con velocidad de 0.5 cm/s, y el apoyo derecho se desplaza hacia la izquierda con la misma velocidad.

• El peso mg de la barra se ha tomado igual a una unidad

Observamos el acercamiento de los apoyos y el movimiento de la barra. En la parte derecha, se muestran los valores de las distancias, D₁, D₂, … D_n en los instantes en los que los apoyos cambian, pasando de deslizar a estar en reposo relativo a la barra o viceversa. En la simulación, el movimiento se detiene cuando la distancia entre los apoyos es inferior a D=10 cm.

Debajo de cada apoyo, se indican los valores de la fuerza normal N₁ y N₂, respectivamente. En la parte superior, se muestran los valores de la distancia d₁ del apoyo izquierdo al c.m., y la distancia d₂ del apoyo derecho al c.m. Finalmente, el valor de la fuerza de rozamiento f₁=f₂= μ_k·N₁,₂. entre la barra y cada uno de los apoyos.

Referencias

Denny M. Stick-slip motion: an important example of self-excited oscillation. Eur. J. Phys. 25, (2004), pp. 311-322.